模式分解算法-满足3NF的无损且保持函数依赖的分解算法、满足BCNF的无损连接分解算法
一、引言
1、对指定的关系模式,若范式级别较低,为第一范式或第二范式,由于存在数据冗余或更新异常问题,在实际中一般是不可用的,关系模式的规范化就是将满足低一级的关系模式分解为若干满足高一级范式的关系模式的集合
2、在函数依赖范围内,希望分解消除数据冗余与操作异常等问题,得到的关系模式均能达到BCNF,并且分解具有无损连接性,同时分解保持函数依赖,但这三个目标有时不能同时满足,一般只能做到如下两点
(1)可以保证分解既具有无损连接性又保持函数依赖,但不能保证分解后的各关系模式属于BC范式,但可以都属于3NF
(2)可以保证分解后的各关系模式都属于BC范式,但只能保证分解再具有无损连接性,不能保证分解保持函数依赖
因此,在实际应用时应根据具体的需求来选择模式分解的方式
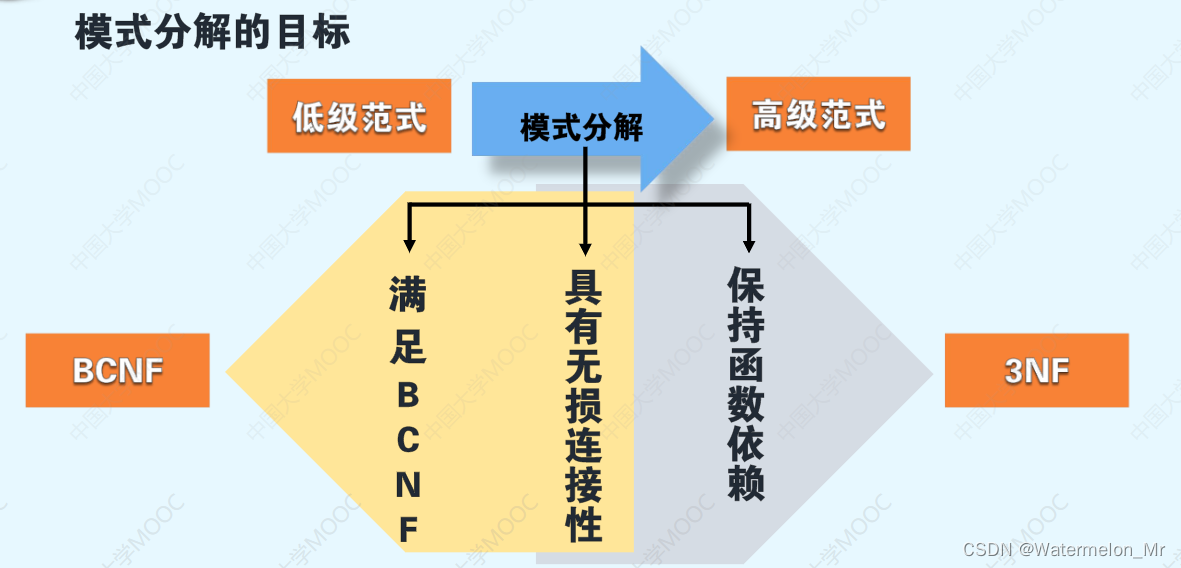
二、满足3NF的无损且保持函数依赖的分解算法
算法4:分解关系模式为满足3NF的一个无损且保持函数依赖的分解
1、输入、输出
输入:
关系模式R(U,F)
输出:
由R分解出的一个关系模式集合,
中每个关系模式属于3NF,且分解具有无损连接性并保持函数依赖关系模式集合
2、算法实现流程
(1)寻找F的最小函数依赖集,令
(2)对F中的函数依赖集按具有相同左部的原则分组,每一分组中的函数依赖集,所涉及的全部属性组成一个属性集
,若
,就去掉
(3)若均不包含R的候选键(此处说明必须求出R中所有的候选键),则增加一个只包含候选键的属性集
;
(4)将及F在
上的投影
构成分解
中的一个关系模式
3、举例:

分析:
(1)由于分解中的关系模式
中包含了R中的候选键,可用判断一个分解是否为无损连接分解的算法来验证分解
具有无损连接性,可验证结果表中包含候选键的关系模式所在的行一定可称为全a
(2)由于F是最小函数依赖集每个分组上的函数依赖的左部相同,分解中的每个关系模式
,一定是一个以函数依赖左部为码的3NF,即使对于
包含于
,
包含于
的情况,也只是在分解结果的
和
中,增加了主属性对于候选键的部分或传递函数依赖,因此
是所求分解
四、满足BCNF的无损连接分解算法
算法5:分解关系模式为满足BCNF的一个无损连接分解
1、输入和输出
输入:
关系模式R(U,F)
输出:
由R分解出的一个关系模式集合,
中每个挂你模式都属于BCNF,且分解具有无损连接性
2、递归算法实现流程:
(1)判断R是否属于BCNF,若是,则返回={R};
(2)R不属于BCNF,必有函数依赖,X不是R的候选键,计算
,将R分解为
和
,
;
(3)对F在和
进行投影,得到
和
;
(4)返回第(1)步,递归地分解和
,返回分解得到的结果集合。
3、举例:




分析:
因为在关系模式中,包含了R的一个候选键HS,利用判断一个分解是否是无损连接分解的算
法,可以验证该分解具有无损连接性
五、小结
(1)利用不同的模式分解算法可按不同的分解目标实现关系模式的规范化设计
(2)数据库设计者在设计关系数据库时,一般尽可能设计成BCNF模式集
相关文章:
模式分解算法-满足3NF的无损且保持函数依赖的分解算法、满足BCNF的无损连接分解算法
一、引言 1、对指定的关系模式,若范式级别较低,为第一范式或第二范式,由于存在数据冗余或更新异常问题,在实际中一般是不可用的,关系模式的规范化就是将满足低一级的关系模式分解为若干满足高一级范式的关系模式的集合…...
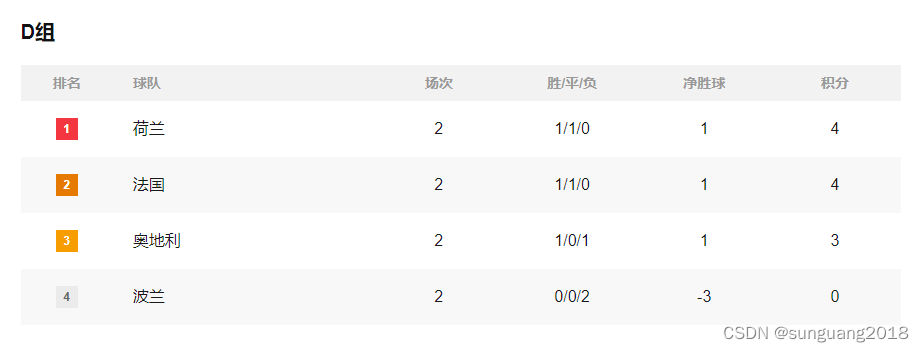
荷兰与法国战平,双方能携手出现?
就在昨天晚上,荷兰队经历了90分钟的鏖战,最终0-0与法国队握手言和。此役,哈维-西蒙斯为荷兰队打进一球,但进球被判无效。从目前的积分形势来看,双方基本上确定携手晋级16强赛。本场比赛,荷兰队后卫内森-阿克…...

数据可视化实验二:回归分析、判别分析与聚类分析
目录 一、使用回归分析方法分析某病毒是否与温度呈线性关系 1.1 代码实现 1.2 线性回归结果 1.3 相关系数验证 二、使用判别分析方法预测某病毒在一定的温度下是否可以存活,分别使用三种判别方法,包括Fish判别、贝叶斯判别、LDA 2.1 数据集展示&am…...

FL论文专栏|设备异构、异步联邦
论文:Asynchronous Federated Optimization(12th Annual Workshop on Optimization for Machine Learning) 链接 实现Server的异步更新。每次Server广播全局Model的时候附带一个时间戳,Client跑完之后上传将时间戳和Model同时带回…...
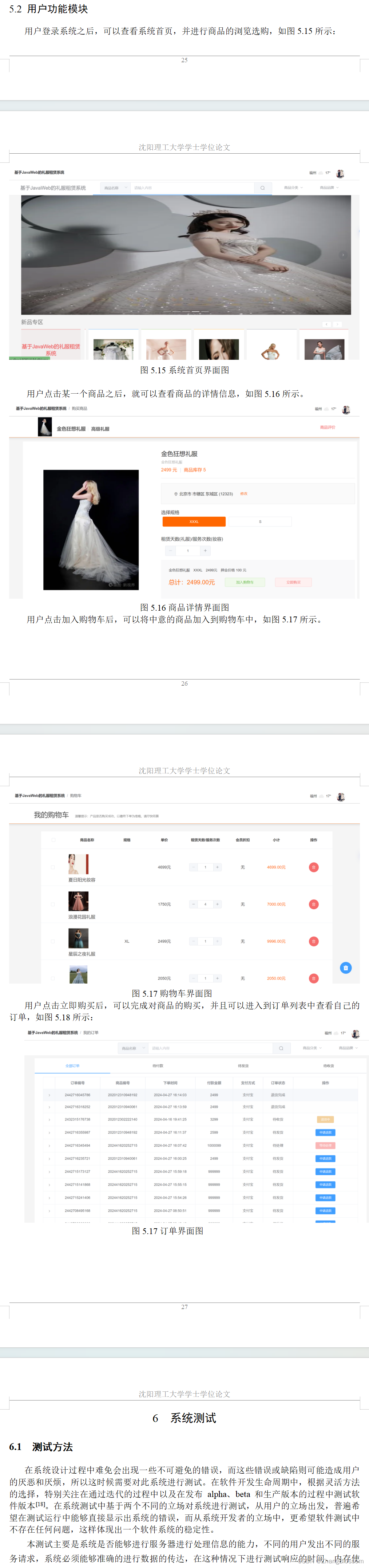
【Java毕业设计】基于JavaWeb的礼服租赁系统
文章目录 摘 要Abstract目录1 绪论1.1 课题背景和意义1.2 国内外研究现状1.2.1 国外研究现状 1.3 课题主要内容 2 开发相关技术介绍2.1 Spring Boot框架2.2 Vue框架2.3 MySQL数据库2.4 Redis数据库 3 系统分析3.1 需求分析3.1.1 用户需求分析3.1.2 功能需求分析 3.2 可行性分析…...

代码随想录训练营Day 66|卡码网101.孤岛的总面积、102.沉没孤岛、103.水流问题、104.建造最大岛屿
1.孤岛的总面积 101. 孤岛的总面积 | 代码随想录 代码:(bfs广搜) #include <iostream> #include <vector> #include <queue> using namespace std; int dir[4][2] {1,0,0,1,-1,0,0,-1}; int count; void bfs(vector<vector<int>>&a…...

根据状态转移写状态机-二段式
目录 描述 输入描述: 输出描述: 描述 题目描述: 如图所示为两种状态机中的一种,请根据状态转移图写出代码,状态转移线上的0/0等表示的意思是过程中data/flag的值。 要求: 1、 必须使用对应类型的状…...

PyTorch C++扩展用于AMD GPU
PyTorch C Extension on AMD GPU — ROCm Blogs 本文演示了如何使用PyTorch C扩展,并通过示例讨论了它相对于常规PyTorch模块的优势。实验在AMD GPU和ROCm 5.7.0软件上进行。有关支持的GPU和操作系统的更多信息,请参阅系统要求(Linux…...
Hadoop archive
Index of /dist/hadoop/commonhttps://archive.apache.org/dist/hadoop/common/...

R语言——R语言基础
1、用repeat、for、while计算从1-10的所有整数的平方和 2、编写一个函数,给出两个正整数,计算他们的最小公倍数 3、编写一个函数,让用户输入姓名、年龄,得出他明年的年龄。用paste打印出来。例如:"Hi xiaoming …...

VFB电压反馈和CFB电流反馈运算放大器(运放)选择指南
VFB电压反馈和CFB电流反馈运算放大器(运放)选择指南 电流反馈和电压反馈具有不同的应用优势。在很多应用中,CFB和VFB的差异并不明显。当今的许多高速CFB和VFB放大器在性能上不相上下,但各有其优缺点。本指南将考察与这两种拓扑结构相关的重要考虑因素。…...
)
elasticsearch安装(centos7)
先给出网址 elasticsearch:Download Elasticsearch | Elastic elasticKibana:Download Kibana Free | Get Started Now | Elastic Logstash:Download Logstash Free | Get Started Now | Elastic ik分词:Releases infinilabs/…...
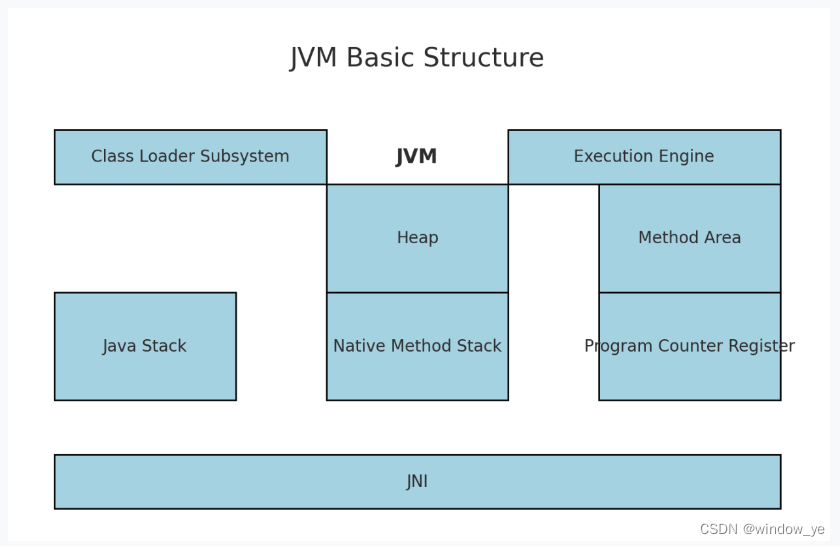
Java高手的30k之路|面试宝典|精通JVM(二)
JVM基本结构 类加载子系统:负责将.class文件加载到内存中,并进行验证、准备、解析和初始化。运行时数据区:包括堆(Heap)、方法区(Method Area)、Java栈(Java Stack)、本…...
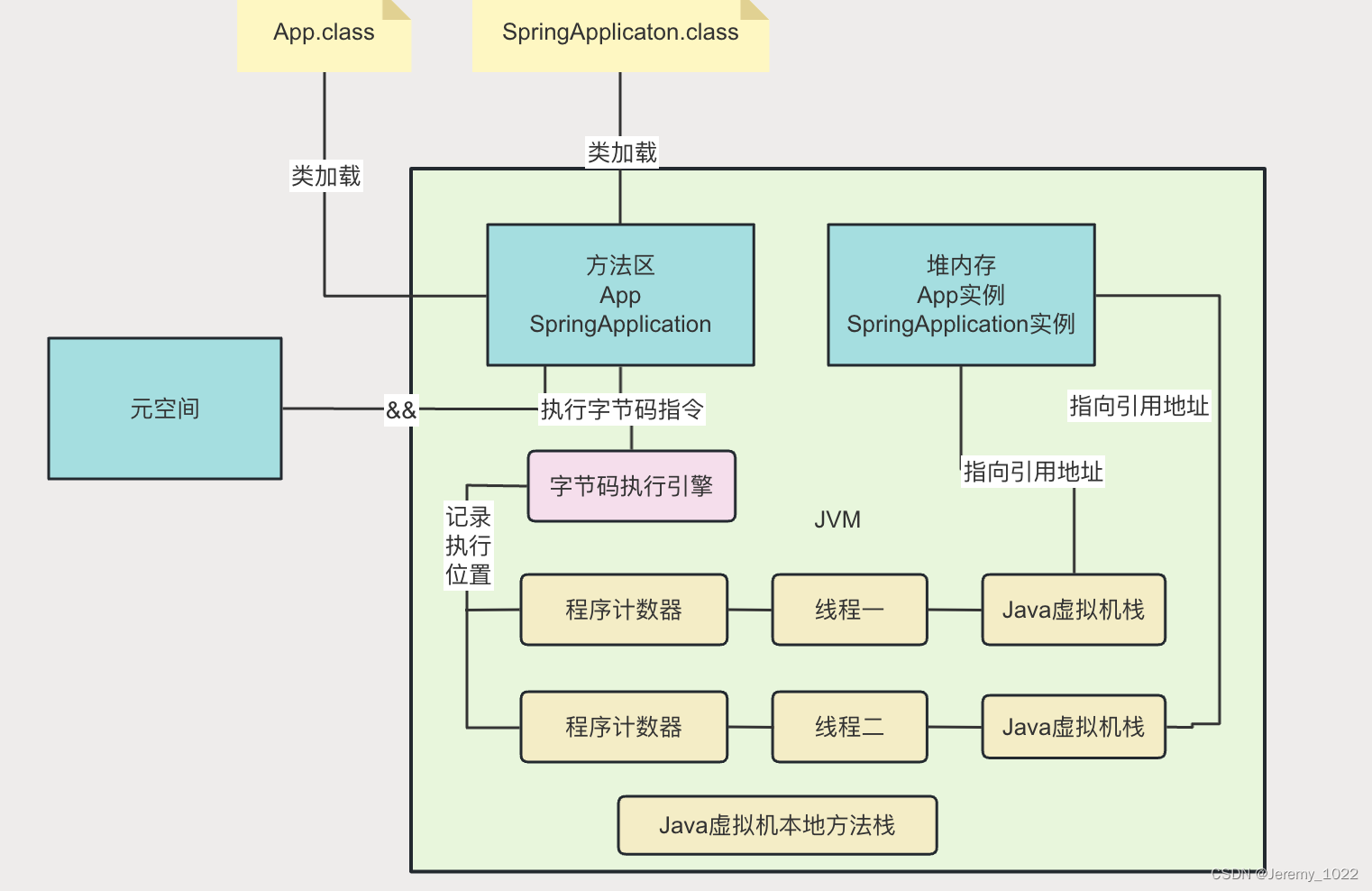
JVM专题六:JVM的内存模型
前面我们通过Java是如何编译、JVM的类加载机制、JVM类加载器与双亲委派机制等内容了解到了如何从我们编写的一个.Java 文件最终加载到JVM里的,今天我们就来剖析一下这个Java的‘中介平台’JVM里面到底长成啥样。 JVM的内存区域划分 Java虚拟机(JVM&…...

学习java第一百零七天
解释JDBC抽象和DAO模块 使用JDBC抽象和DAO模块,我们可以确保保持数据库代码的整洁和简单,并避免数据库资源关闭而导致的问题。它在多个数据库服务器给出的异常之上提供了一层统一的异常。它还利用Spring的AOP模块为Spring应用程序中的对象提供事务管理服…...
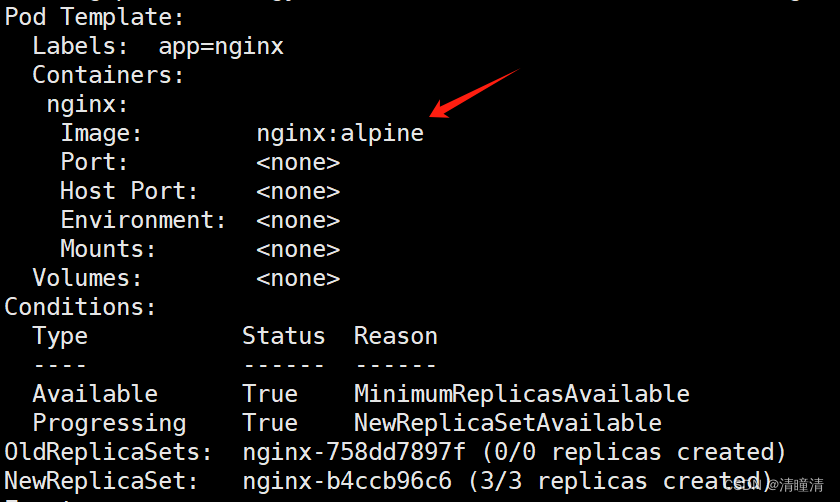
k8s上尝试滚动更新和回滚
滚动更新和回滚 实验目标: 学习如何进行应用的滚动更新和回滚操作。 实验步骤: 创建一个 Deployment。更新 Deployment 的镜像版本,观察滚动更新过程。回滚到之前的版本,验证回滚操作。 今天呢,我们继续来进行我们k…...
GitHub Copilot 登录账号激活,已经在IntellJ IDEA使用
GitHub Copilot 想必大家都是熟悉的,一款AI代码辅助神器,相信对编程界的诸位并不陌生。 今日特此分享一项便捷的工具,助您轻松激活GitHub Copilot,尽享智能编码之便利! GitHub Copilot 是由 GitHub 和 OpenAI 共同开…...
)
进程知识点(二)
文章目录 一、进程关系?二、孤儿态进程(Orphan)定义危害处理 三、僵尸进程定义处理 四、守护进程(Daemon )定义作用 总结 一、进程关系? 亲缘关系:亲缘关系主要体现于父子进程,子进程父进程创建,代码继承于父进程&…...

【线性代数】【一】1.6 矩阵的可逆性与线性方程组的解
文章目录 前言一、求解逆矩阵二、线性方程组的解的存在性总结 前言 前文我们引入了逆矩阵的概念,紧接着我们就需要讨论一个矩阵逆的存在性以及如何求解这个逆矩阵。最后再回归上最初的线性方程组的解,分析其中的联系。 一、求解逆矩阵 我们先回想一下在…...
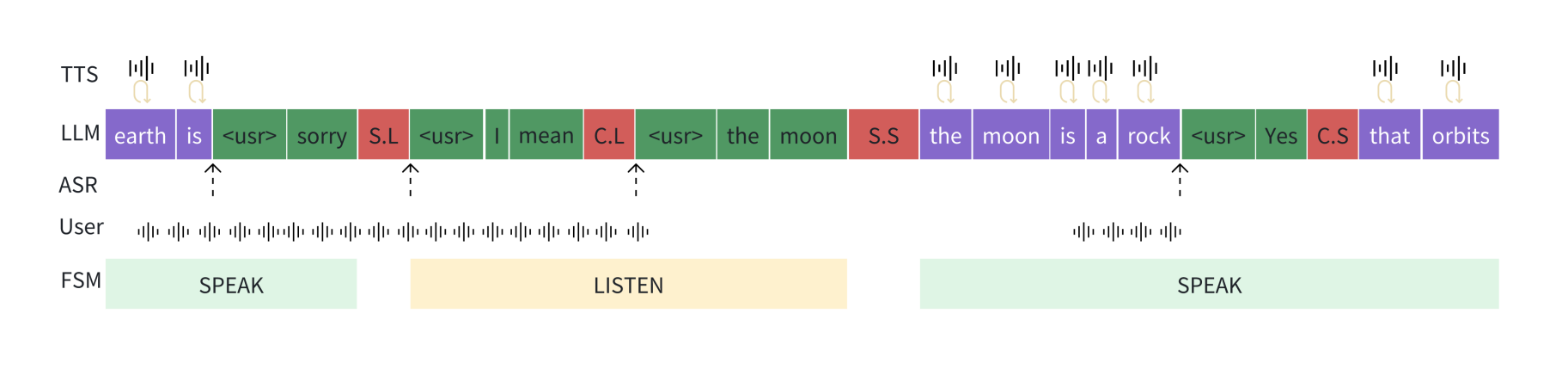
基于大型语言模型的全双工语音对话方案
摘要解读 我们提出了一种能够以全双工方式运行的生成性对话系统,实现了无缝互动。该系统基于一个精心调整的大型语言模型(LLM),使其能够感知模块、运动功能模块以及一个具有两种状态(称为神经有限状态机,n…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
