坚持就是胜利
很多朋友,可能坚持了多年的同等学力申硕考试,依然没有通过。如果你感到困惑,感到迷茫,要坚信:坚持就能胜利。有很多人跟你一样,一直坚持在路上,没有停止脚步。
生活没有你想象的那么好,也没有你想象的那么糟------莫泊桑
以下内容来自网络转载:
最近心情充满了低落、焦虑、困惑,因为论文不知该如何写。整个人似乎丧失了行动力,心里老是想退学。坚持了3年的博士生涯,难道就此放弃?放弃后又该何去何从?
幸得朋友百般劝慰,叫我不要退学,他的一句——“坚持就是胜利”,让我醍醐灌顶,精神得以重新振作!后来又看到了一些关于“坚持就是胜利”的名言名句,内心重燃起生活下去的信心和动力。
很快,我就重新确定人生目标,列出每天该坚持做的事项,并立即行动起来。祈愿下来的日子,自己能做到克服困难,坚持完成“每日事项”,实现目标。
也以此文与一些正在面对困难的朋友共勉。无论遇到什么困难,请鼓起勇气,直面生活,把该做的事情坚持下去做,总有一天目标会实现,因为坚持就是胜利!
把一些关于“坚持就是胜利”的名言名句分享如下:
我达到目标的唯一力量,就是我的坚持精神。——巴斯德
成大事不在于力量的大小,而在于能坚持多久。——塞约翰生
成功的秘诀是走向目的的坚持。——狄斯雷利
伟大的作品不是靠力量,而是靠坚持来完成的。——约翰逊
贵有恒,何必三更起五更眠;最无益,只怕一日曝十日寒。——毛泽东
相关文章:

坚持就是胜利
很多朋友,可能坚持了多年的同等学力申硕考试,依然没有通过。如果你感到困惑,感到迷茫,要坚信:坚持就能胜利。有很多人跟你一样,一直坚持在路上,没有停止脚步。 生活没有你想象的那么好ÿ…...
 或者转置 intrinsic (内参)矩阵的原因)
代码中出现转置 pose (c2w,外参矩阵) 或者转置 intrinsic (内参)矩阵的原因
在代码中见到 pose(c2w),intrinsic 矩阵的转置,觉得比较奇怪。 后来想了一下为什么。下面解释一下: 用 c2w 矩阵举例子。理论上,一个 c2w 左乘上 一个相机坐标系下的点 P的坐标,能够得到该点在…...

2023 年腾讯云服务器配置价格表出炉(2核2G/2核4G/4核8G/8核16G、16核32G)
腾讯云轻量应用服务器为轻量级的云服务器,使用门槛低,按套餐形式购买,轻量应用服务器套餐自带的公网带宽较大,4M、6M、7M、10M、14M及20M套餐可选,如果是云服务器CVM这个带宽价格就要贵很多了。 1、轻量应用服务器优惠…...
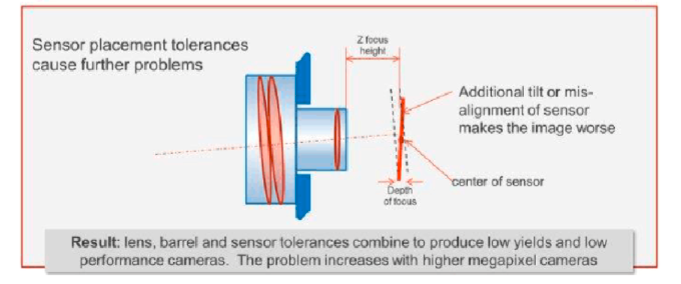
相机出图画面一半清晰,一半模糊的原因是什么?
1、问题背景:在做项目的过程中,有遇到过几次,出图后画面是一半清晰,一半模糊的现象,再重新对焦也是一样。但换了个镜头后就好了,这应该是镜头的质量问题,但导致镜头出现这种问题的具体原因是什么…...
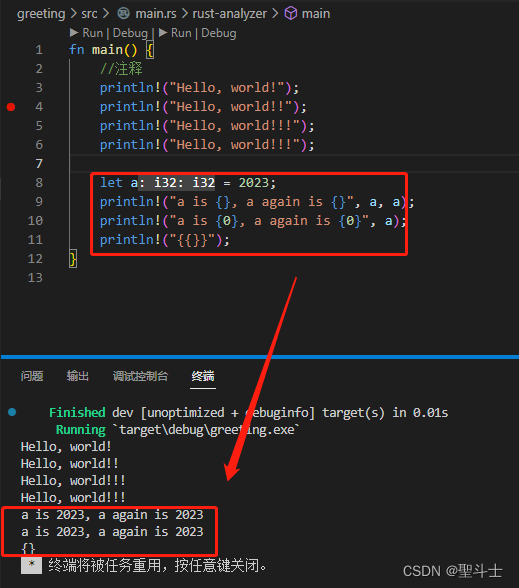
Rust学习入门--【4】Rust 输出到命令行
Rust 语言中的打印“函数” 学习新的编程语言时,大家都喜欢打印“Hello World”。 在Rust中怎样将字符串打印出来呢? Rust 输出文字的方式主要有两种:println!() 和 print!()。 “函数”差异说明: 这两个"函数"都是向…...

Vector刷写方案—vFlash工具介绍
我是穿拖鞋的汉子,魔都中坚持长期主义的工科男! 今天魔都天气是连阴雨,滴滴答答的下个不停,心情也跟着潮湿起来!老规矩分享一段喜欢的文字,避免成为高知识低文化的工程师: 即使在真正的困境里,也一直提示自己,每次自恋不得超过十分钟! 那些看似无法度过得困境,不是…...
》)
【阶段总结】《非结构化信息分析应用与实践(筹)》
《非结构化信息分析应用与实践(筹)》Part 1.知识储备一、机器学习 1.几种常见的有监督学习算法 2.几种常见的无监督学习算法 3.数据挖掘基础知识 30 问 二、神经网络与深度学习 1.MP神经网络模型(附实例代码讲解) 2.图解LST…...
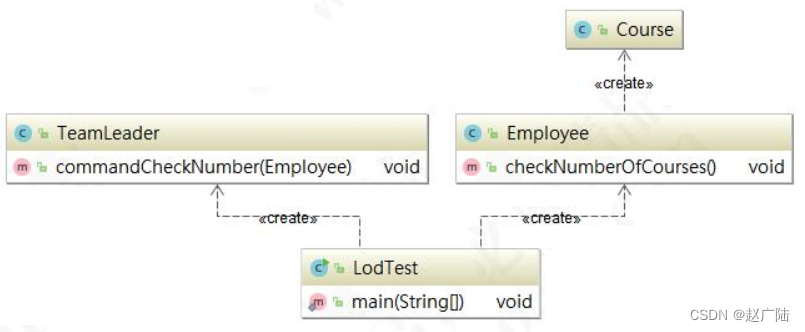
七大设计原则之迪米特法则应用
目录1 迪米特法则介绍2 迪米特法则应用1 迪米特法则介绍 迪米特原则(Law of Demeter LoD)是指一个对象应该对其他对象保持最少的了解,又叫最少知 道原则(Least Knowledge Principle,LKP),尽量降低类与类之…...

curl命令用法精简整理
目录1.GET请求1.1 形式1:1.2 形式2:2.POST请求2.1 无入参:2.2 form传参(文件):2.3 json入参:2.4 json文件入参:3.请求计时3.1 time命令(Linux):3.…...

Fluent Python 笔记 第 5 章 一等函数
在 Python 中,函数是一等对象。编程语言理论家把“一等对象”定义为满足下述条件的程 序实体: 在运行时创建能赋值给变量或数据结构中的元素 • 能作为参数传给函数能作为函数的返回结果 5.1 把函数视作对象 会用 map。 5.2 高阶函数 接受函数为参数࿰…...

卡尔曼滤波器与DSP实现
卡尔曼滤波器是利用系统状态方程,结合测量结果对系统状态进行进行最优估计的算法。本文介绍它的主要公式,并举例在C6000 DSP上实现。 推荐资料 KalmanFilter.NETUnderstanding Kalman Filters卡尔曼滤波与组合导航原理 “If you can’t explain it sim…...

引入QQ邮箱发送验证码进行安全校验
最近想给自己的项目在注册时加点安全校验,本想着使用短信验证码,奈何囊中羞涩只能退而求次改用QQ邮箱验证注册~ 一.需求分析 场景:用户输入自己的邮箱,点击获取验证码,后台会发送一封邮件到对应邮箱中。 分析&#x…...

【c++】数组
文章目录一维数组定义方式数组名案例案例1:元素逆置案例2:冒泡排序二维数组定义方式数组名案例:考试成绩统计数组特点: 1、每个数据元素放在一块连续的内存空间中; 2、数组中每个数据元素都是相同数据类型;…...
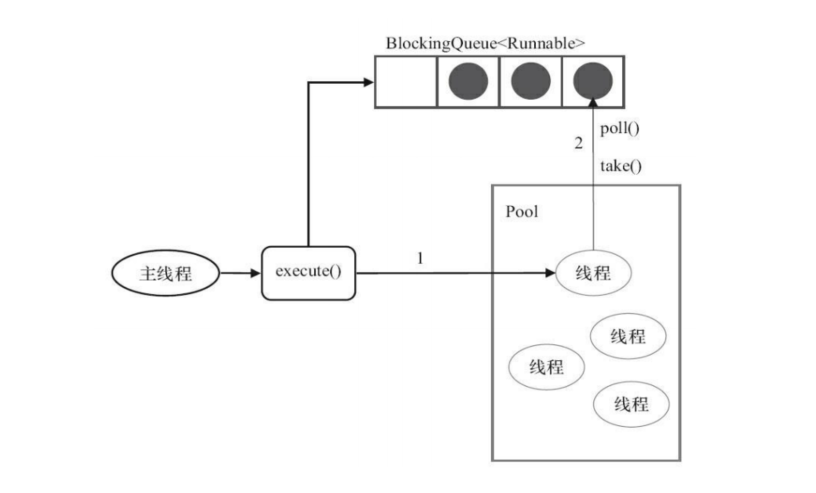
线程池的简单实现:Java线程池初学者必读指南
"作为一名Java开发者,是否曾经遇到过多线程并发的问题?线程数量过多时,会导致资源浪费,应用性能下降,甚至发生线程死锁的情况。那么,有没有一种方法可以有效地管理线程,避免这些问题呢&…...

【C#】[带格式的字符串] 复合格式设置字符串与使用 $ 的字符串内插 | 如何格式化输出字符串
复合格式输出 string name "Fred"; String.Format("Name {0}, hours {1:hh}", name, DateTime.Now);通过指定相同的参数说明符,多个格式项可以引用对象列表中的同一个元素。 例如,通过指定“0x{0:X} {0:E} {0:N}”等复合格式字符…...

Lecture4 反向传播(Back Propagation)
目录 1 问题背景 1.1计算图(Computational Graph) 1.2 激活函数(Activation Function)引入 1.3 问题引入 2 反向传播(Back Propagation) 2.1 为什么要使用反向传播 2.2 前馈运算(Forward Propagation…...
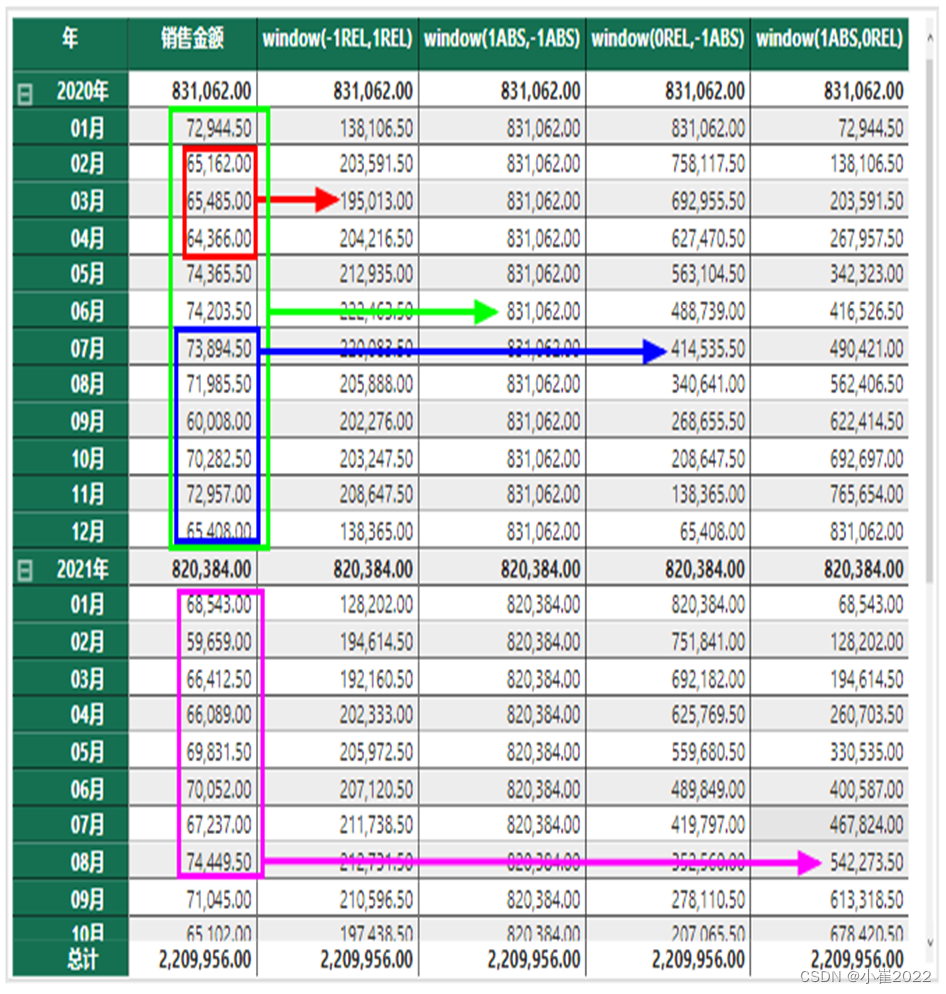
Power BI 筛选器函数---Window实例详解
一、Window函数 语法: Window ( <起始位置>,<起始位置类型>,<结束位置>,<结束位置类型>, [<关系>], [<OrderBy>],[空白],[PartitionBy] ) 含义: 对指定分区(PartitioinBy)中的行(关系表&…...

基础篇—如何创建css样式表,并集成到html文件中?
CSS 创建 HTML相当于一个页面的结构,CSS相当于页面的装饰,浏览器当读到一个样式表时,浏览器会根据它来格式化 HTML 文档。 如何插入样式表 插入样式表的方法有三种: 外部样式表(External style sheet)内部样式表(Internal style sheet)内联样式(Inline style)1、外…...

WindowsServer服务器系列:部署FTP文件服务
1、点击“开始”菜单,选择“服务器管理器” 2、在接下来弹出页面中选择“添加角色和功能” 3、接下来点击“下一步” 4、接下来选择“基于角色或基于功能的安装”并点击“下一步” 5、选择“从服务器池中选择服务器”并点击“下一步” 6、接下来选中“Web 服务器(II…...
| 真题+思路+代码)
华为OD机试 - 数字加减游戏(Python)| 真题+思路+代码
数字加减游戏 题目 小明在玩一个数字加减游戏,只使用加法或者减法,将一个数字 s 变成数字 t。 每个回合,小明可以用当前的数字加上或减去一个数字。 现在有两种数字可以用来加减,分别为 a,b(a!=b),其中 b 没有使用次数限制。 请问小明最少可以用多少次 a,才能将数字 s …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
