Lecture4 反向传播(Back Propagation)
目录
1 问题背景
1.1计算图(Computational Graph)
1.2 激活函数(Activation Function)引入
1.3 问题引入
2 反向传播(Back Propagation)
2.1 为什么要使用反向传播
2.2 前馈运算(Forward Propagation)过程
2.3 反向传播过程
2.3.1 计算过程
2.3.2 课堂练习
3 在Pytorch中进行前馈和反向传播计算
3.1 Tensor数据类型
3.2 代码实现
3.2.1 实现线性模型
1 问题背景
1.1计算图(Computational Graph)
计算图(Computational Graph)是一种用于表示数学运算的图形模型。在计算图中,每个节点代表一个数学运算,而每条边代表运算之间的输入输出关系。
计算图用于记录和组织复杂的数学运算,可以帮助我们快速理解运算的依赖关系和结构。在机器学习和深度学习中,计算图是一种常用的工具,用于定义和计算模型的损失函数和梯度。
计算图还可以用于求导,通过利用计算图上的梯度进行反向传播,可以快速计算模型的损失函数对于每个参数的导数。因此,计算图不仅提高了计算效率,而且可以方便地实现自动微分和反向传播。
比如下式

用计算图表示
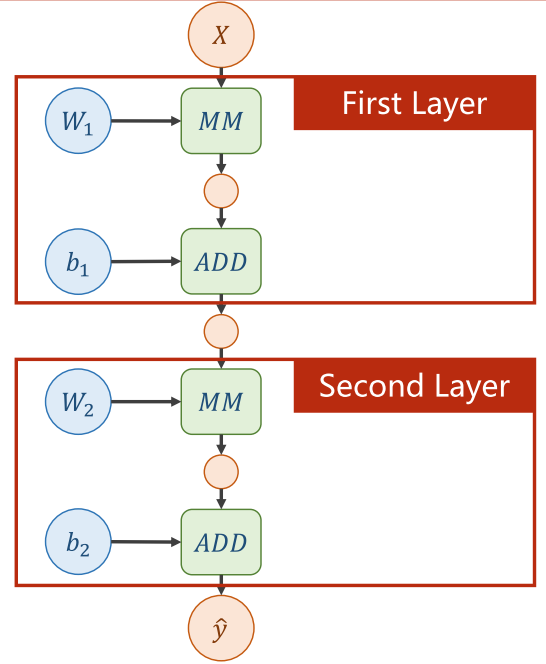
注:MM表示相乘
1.2 激活函数(Activation Function)引入
对于刚刚举例的神经网络计算图,计算机会直接对其进行简化:
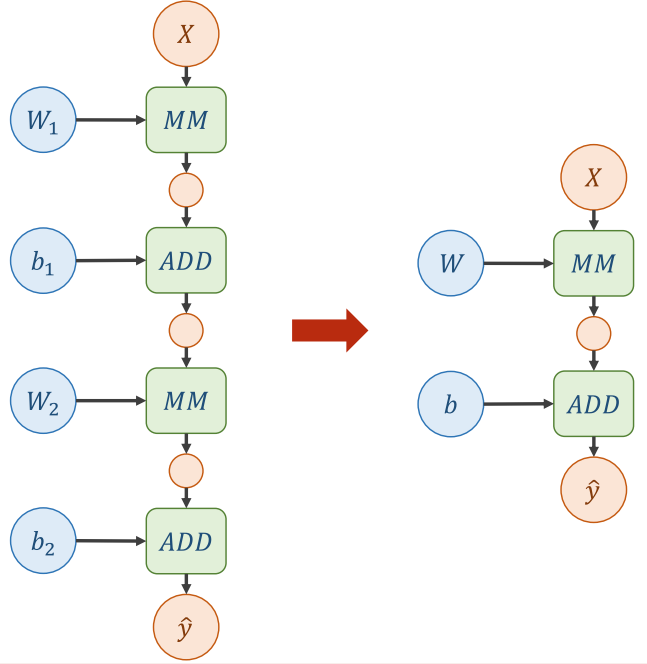
这就导致了计算过程中添加的新的权重值变得毫无意义,层数的划分变得多余,导致神经网络的表示能力下降。
为了解决这个问题,我们需要在每一层的输出处应用上一个非线性变换函数(Nonlinear
Function),这样模型就不会被简化了

如果一个神经网络只使用线性变换函数,那么其最终的表示能力仍然有限,因为它们的输出结果是线性的,无法对复杂的数据进行分类或回归。因此,在每一层的输出都应用非线性变换函数,以增强神经网络的表示能力。
非线性变换函数通常也称为激活函数(Activation Function)。常见的激活函数有Sigmoid函数、ReLU函数等。
补充
线性函数与非线性函数的简单区别:线性函数其函数图像是一条直线;非线性函数的函数图像是一条曲线,等等。
1.3 问题引入
对于一个简单线性模型 ,我们可以利用解析式来进行简单的计算。

通过计算图,我们可以直观地看出计算的过程:
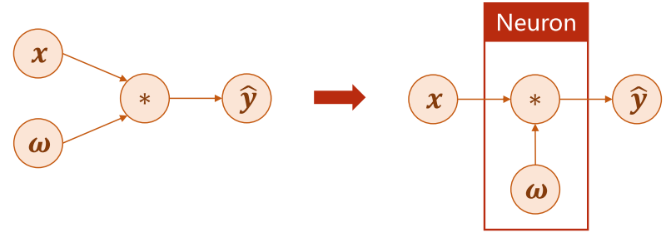
然后利用解析式来更新权重:

但是对于复杂的神经网络模型来说,可能同时含有多个𝜔,如果为每个𝜔写解析式来计算,任务会非常繁重,且解析式也会变得很复杂:
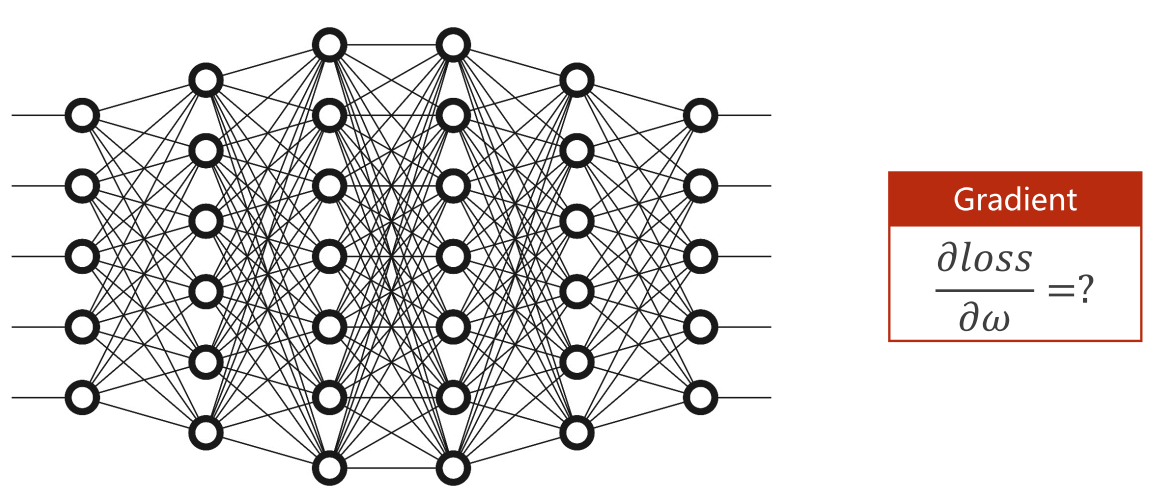
复杂的神经网络模型往往具有大量的权重,如果使用手动计算权重导数的方法,这将是一项非常复杂且繁琐的任务。
2 反向传播(Back Propagation)
2.1 为什么要使用反向传播
如果使用手动计算权重导数的方法来计算复杂神经网络模型,将会非常困难。而反向传播(Back Propagation)可以使用链式法则自动计算损失函数对于每个权重的导数,大大减少计算复杂度,使训练神经网络变得更加有效。
除此之外,反向传播还有一个优点:实现最优化,省去了重复求导的步骤,以及更高效地去计算偏导。详情请参考相关链接,这里不展开:
http://t.csdn.cn/igONJ
https://zhuanlan.zhihu.com/p/25081671
2.2 前馈运算(Forward Propagation)过程

简单来说,就是 x和𝜔进行f(x, 𝜔)操作后得出z,然后把z值应用到Loss中去。
比如𝑓 = 𝑥 ∙ 𝜔, 𝑥 = 2, 𝜔 = 3
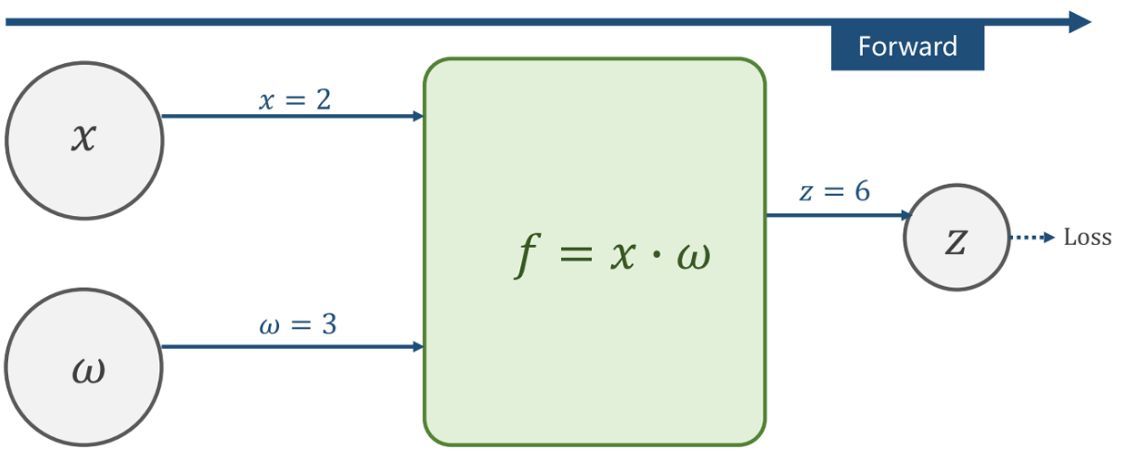
2.3 反向传播过程
2.3.1 计算过程

其中以下两个局部函数是由z=𝑥 ∙ 𝜔,分别对x和对𝜔求导得到的:
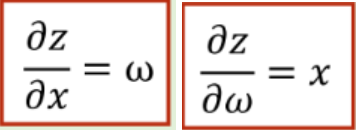
简单来说,就是沿着正方向相反的方向,为每个节点乘上局部导数后,再传递给下一个节点。
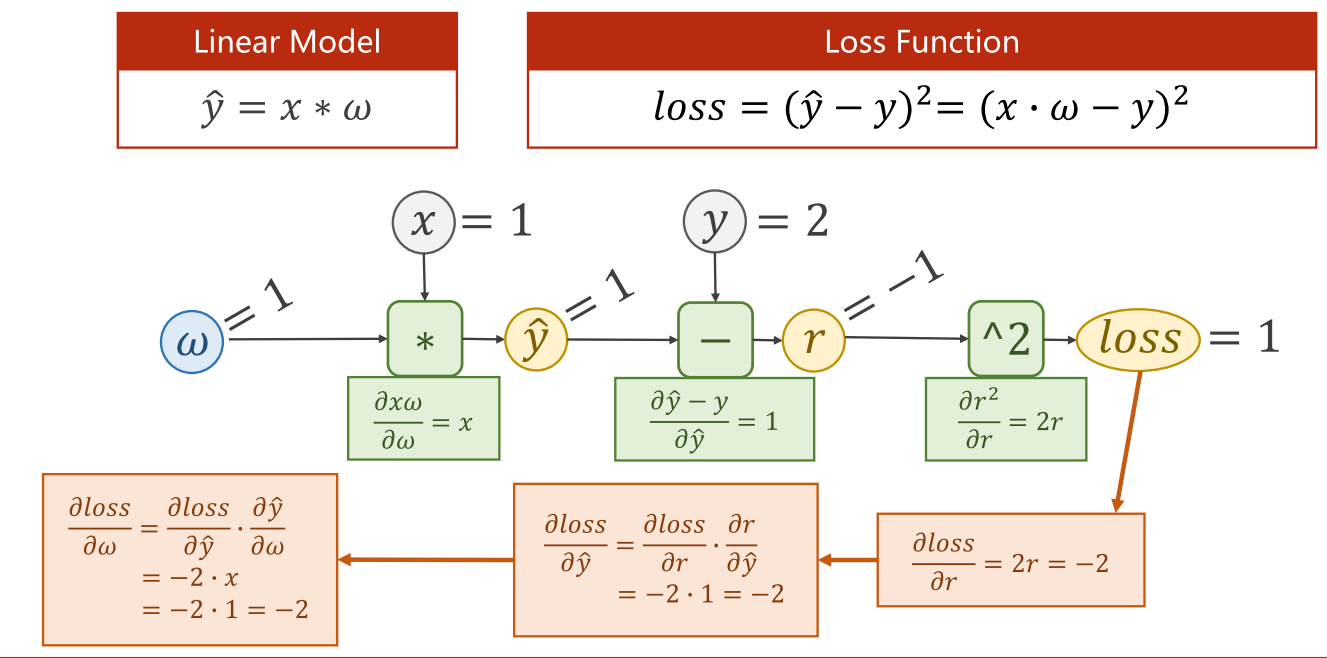
2.3.2 课堂练习
(1)计算梯度
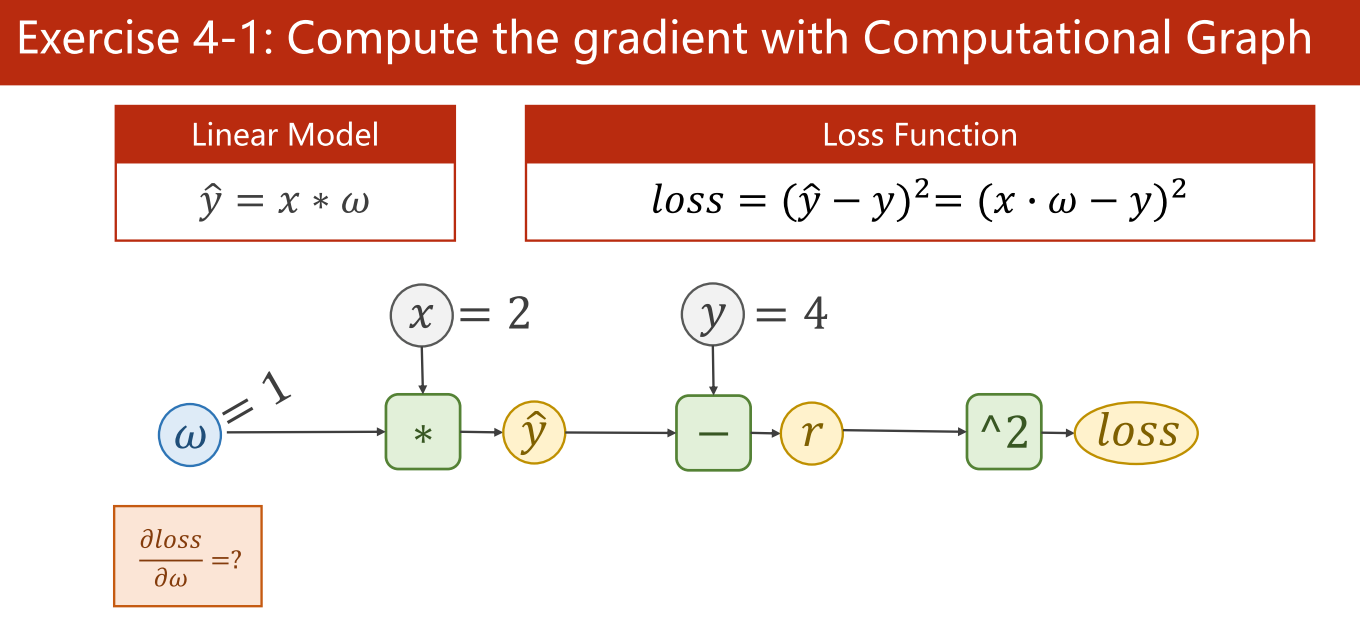
答案:-8
(2)计算加上偏差值后的梯度(计算仿射模型的梯度)
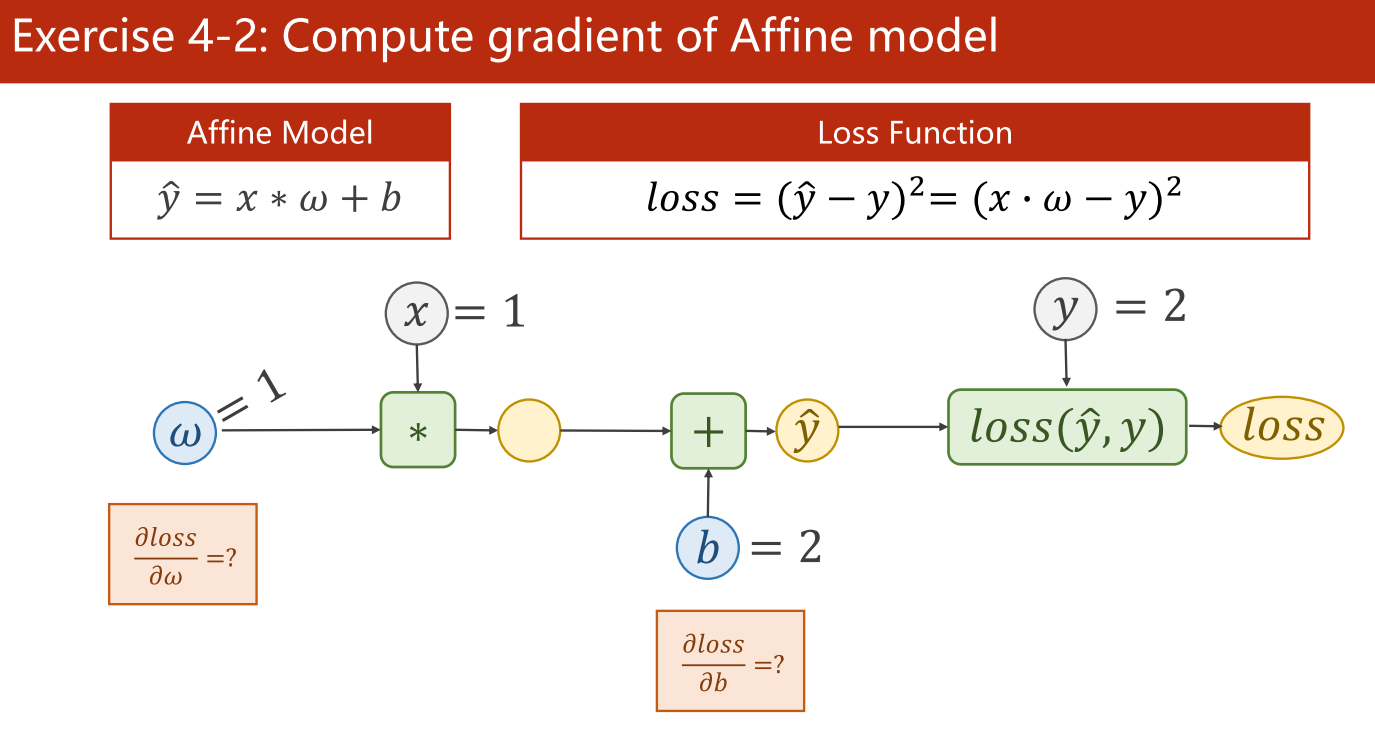
答案:2,2
3 在Pytorch中进行前馈和反向传播计算
3.1 Tensor数据类型

3.2 代码实现
3.2.1 实现线性模型
课堂上的案例,补充了些解释:
import torchx_data = [2.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = torch.Tensor([1.0]) # 创建了一个一维张量,包含单一数值1.0,作为权重初始值
w.requires_grad = True # w=torch.Tensor([1.0])创建了一个张量,然后使用 w.requires_grad = True设置该张量需要求导,于是PyTorch 会记录对该张量的操作,以便在反向传播时进行梯度更新def forward(x):return x * w # 注意这里的x已经自动转换为Tensor类型,原本是list类型def loss(x, y):y_pred = forward(x)return (y_pred - y) ** 2print("predict (before training)", 4, forward(4).item())
for epoch in range(100):for x, y in zip(x_data, y_data):l = loss(x, y)# 反向传播,这句还可以清空释放计算图,避免计算图堆砌在内存中。# 若在当前backward()后,不执行forward() 而是执行另一个backward(),# 则需要在当前backward()时,指定保留计算图,backward(retain_graph)# 换言之,想要保留计算图,则写成backward(retain_graph)l.backward()# 使用item将一个张量转换成一个 Python标量,也是为了防止产生计算图# 一般在进行数学运算时使用grad.data,而在输出梯度数值时使用grad.item()# 一般梯度只有一个元素,所以使用.item()# 可以方便地把梯度值转换为一个数字。print('\tgrad:', x, y, w.grad.item())# 这句代码用来更新权重# 这里使用w.grad.data而不是w.grad是为了防止建立计算图,我们只是对数值做修改,而不是对模型做出修改# 虽然w.data 也是 tensor 类型的数据,# 但它是不需要 gradient 的,因此不会建立计算图,只是在数值范围上发生变化w.data = w.data - 0.01 * w.grad.dataw.grad.data.zero_() # 每次反向传播前,需要清空梯度缓存,以避免之前的梯度对当前梯度造成影响。print("progress:", epoch, l.item()) # 轮数,每轮训练完后对应的loss值,l是tensor类型,所以用item取出值来
print("predict (after training)", 4, forward(4).item())简单来说,每一轮,数据都会先前馈运算出loss,再反向运算出新的梯度,然后用梯度来更新权重值。
相关文章:

Lecture4 反向传播(Back Propagation)
目录 1 问题背景 1.1计算图(Computational Graph) 1.2 激活函数(Activation Function)引入 1.3 问题引入 2 反向传播(Back Propagation) 2.1 为什么要使用反向传播 2.2 前馈运算(Forward Propagation…...
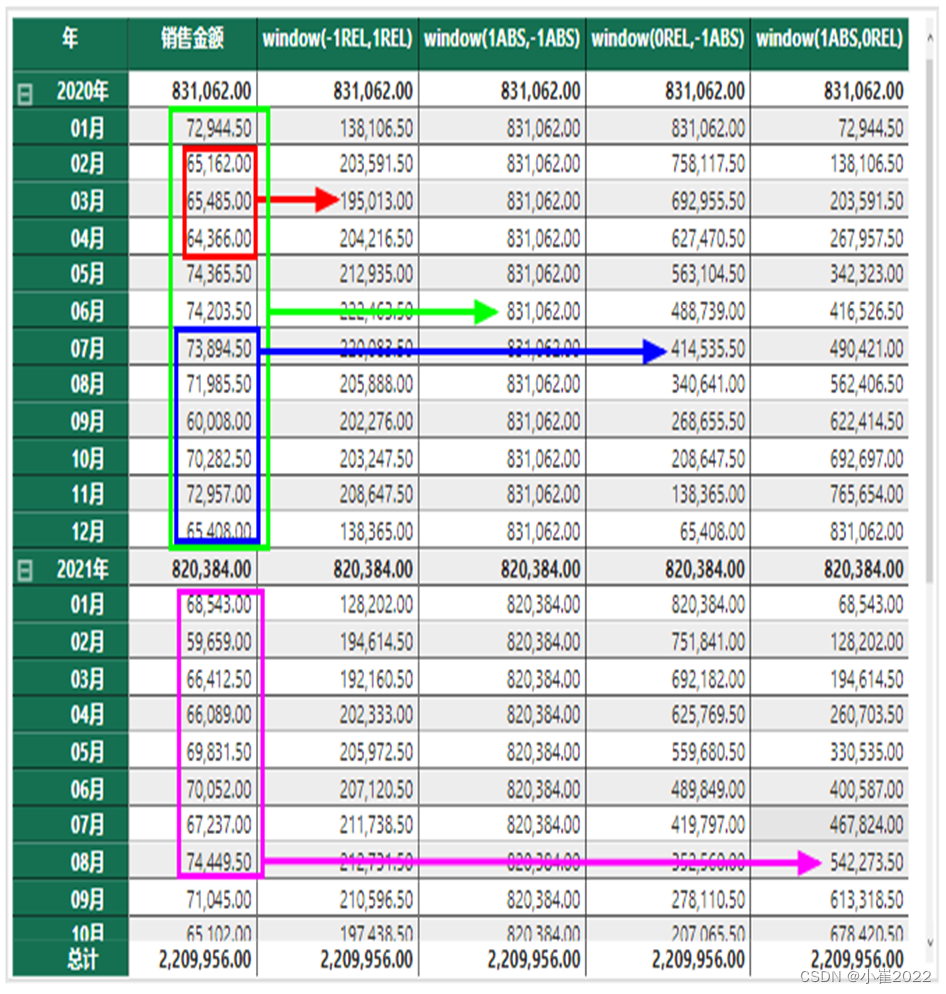
Power BI 筛选器函数---Window实例详解
一、Window函数 语法: Window ( <起始位置>,<起始位置类型>,<结束位置>,<结束位置类型>, [<关系>], [<OrderBy>],[空白],[PartitionBy] ) 含义: 对指定分区(PartitioinBy)中的行(关系表&…...

基础篇—如何创建css样式表,并集成到html文件中?
CSS 创建 HTML相当于一个页面的结构,CSS相当于页面的装饰,浏览器当读到一个样式表时,浏览器会根据它来格式化 HTML 文档。 如何插入样式表 插入样式表的方法有三种: 外部样式表(External style sheet)内部样式表(Internal style sheet)内联样式(Inline style)1、外…...

WindowsServer服务器系列:部署FTP文件服务
1、点击“开始”菜单,选择“服务器管理器” 2、在接下来弹出页面中选择“添加角色和功能” 3、接下来点击“下一步” 4、接下来选择“基于角色或基于功能的安装”并点击“下一步” 5、选择“从服务器池中选择服务器”并点击“下一步” 6、接下来选中“Web 服务器(II…...
| 真题+思路+代码)
华为OD机试 - 数字加减游戏(Python)| 真题+思路+代码
数字加减游戏 题目 小明在玩一个数字加减游戏,只使用加法或者减法,将一个数字 s 变成数字 t。 每个回合,小明可以用当前的数字加上或减去一个数字。 现在有两种数字可以用来加减,分别为 a,b(a!=b),其中 b 没有使用次数限制。 请问小明最少可以用多少次 a,才能将数字 s …...

【c/c++】c语言的自增操作在不同编译器的差别
示例代码 代码如下: #include <stdio.h>#define product(x) ((x)*(x))int main(void) {int i 3, j, k;j product(i); // (i) * (i)k product(i); // (i) * (i)printf("%d %d\n", j, k); }执行结果 在Ubuntu18.04下通过GCC编译和执行的结果…...
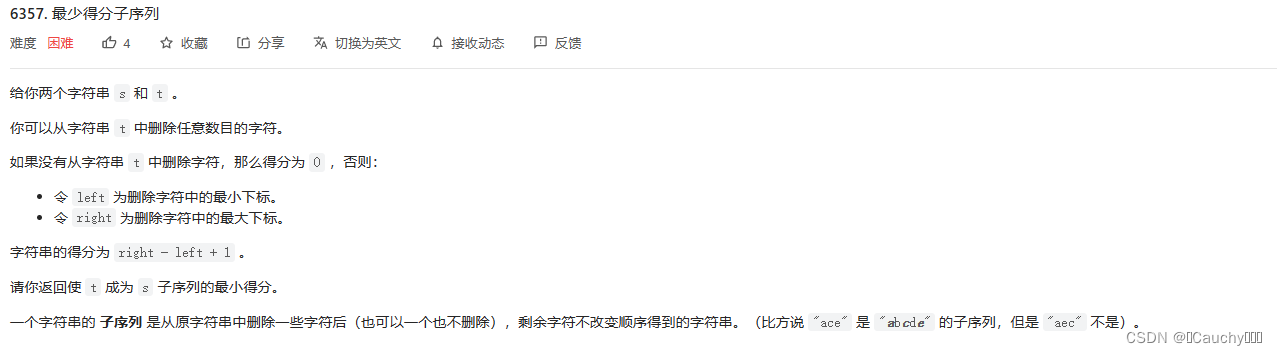
【LeetCode第 332 场周赛】
传送门 文章目录6354. 找出数组的串联值6355. 统计公平数对的数目6356. 子字符串异或查询6357. 最少得分子序列6354. 找出数组的串联值 题目 思路 前后指针 代码 class Solution { public:long long findTheArrayConcVal(vector<int>& nums) {long long res 0;i…...
【蓝桥杯单片机】Keil5中怎么添加STC头文件;从烧录软件中添加显示添加成功后新建工程时依旧找不到
蓝桥杯单片机的芯片型号:IAP15F2K61S2 添加头文件:STC15F2K60S2.H 【1】如何通过烧录软件添加STC头文件: 从ATC-ISP的Keil仿真设置中添加(同时自动下载仿真驱动)仔细阅读添加说明 KEIL5添加STC芯片库_Initdev的博客-…...
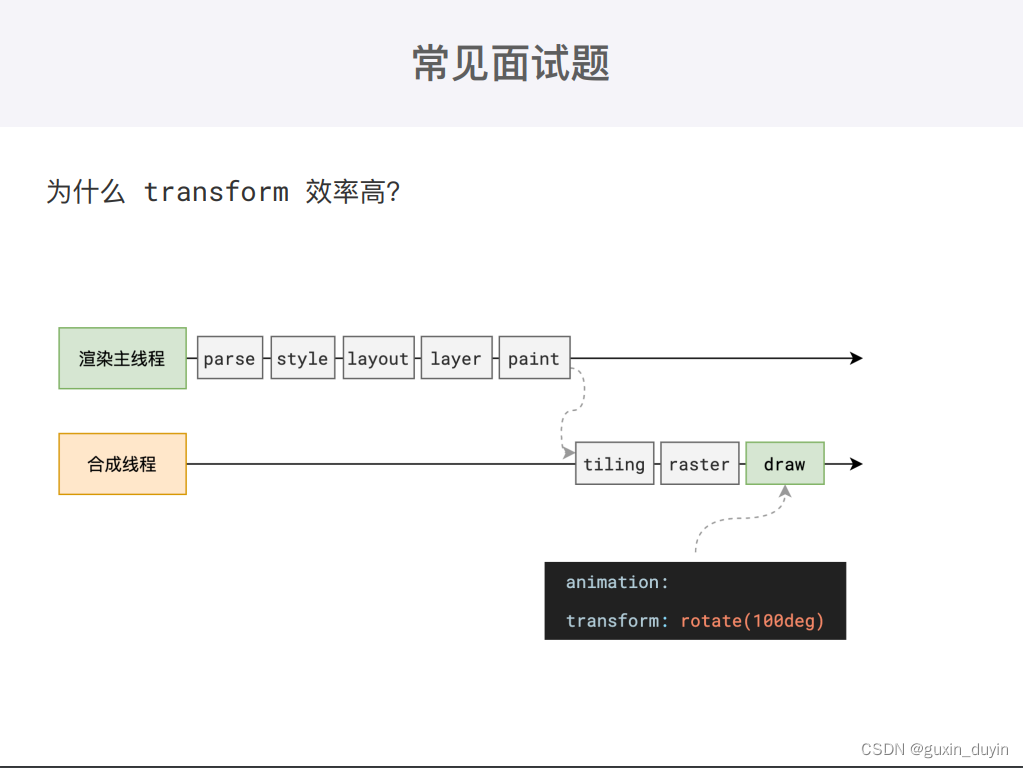
图解浏览器渲染页面详细过程
渲染详细过程 产生渲染任务,开启渲染流程 当浏览器的网络线程收到 HTML 文档后,会产生一个渲染任务,并将其传递给渲染主线程的消息队列。 在事件循环机制的作用下,渲染主线程取出消息队列中的渲染任务,开启渲染流程。…...
)
多线程面试题开胃菜1(5道)
一.多线程有什么用?1)发挥多核CPU 的优势随着工业的进步,现在的笔记本、台式机乃至商用的应用服务器至少也都是双核的,4 核、8 核甚至 16 核的也都不少见,如果是单线程的程序,那么在双核 CPU 上就浪费了 50…...
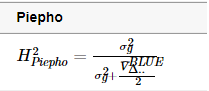
植物育种中广义遗传力的定义
大家好, 我是邓飞。 今天聊一下广义遗传力的计算方法。 广义遗传力定义 广义遗传力(H2H^2H2)定义为归因于基因型总体遗传变异的表型变异比例。 通常他包括三个解释:(详见我这篇博客的公式推导 回归系数 相关系数 遗…...

西瓜书读书笔记—绪论
文章目录机器学习典型的机器学习过程基本术语归纳偏好机器学习 机器学习:致力于研究如果通过计算的手段,利用经验来改善系统自身的性能 在计算机系统中,“经验” 通常以 “数据” 形式存在,因此,机器学习所研究的主要内…...

ES8——Generator函数的使用
babel工具插件下载:npm i --save babel-polyfill 引入:polyfill.js进行转码(es8->es5) 介绍 Generator函数用于生成迭代器 function * (){} yeild: 作用同return类似 {const obj function* () {yield "a";yield 12…...

德馨食品冲刺A股上市:计划募资9亿元,林志勇为实际控制人
近日,浙江德馨食品科技股份有限公司(下称“德馨食品”或“德馨饮料”)预披露更新招股书,准备在上海证券交易所主板上市。据贝多财经了解,德馨食品于2022年7月5日递交上市申请,安信证券为其保荐机构。 本次…...

湿敏电阻的原理,结构,分类与应用总结
🏡《总目录》 0,概述 湿敏电阻是指电阻值随着环境的湿度变化而变化的电阻,本文对其工作原理,结构,分类和应用场景进行总结。 1,工作原理 湿敏电阻是利用湿敏材料制成的,湿敏材料吸收空气中水分时,自身的阻值发生变化。 2,结构 如下图所示,市民电阻包括4个部分构成,…...

千锋教育嵌入式物联网教程之系统编程篇学习-03
目录 进程的终止 exit函数 _exit函数 进程退出清理 进程间的替换 进程间通信 常见通信机制 进程间通信的实质 信号 产生信号的方式 信号的默认处理方式 进程对信号的处理方式 kill函数 进程的终止 使用exit函数对进程进行终止,而return只是结束函数&a…...
升级到https
现在很多站长都会考虑将自己的站点从http升级到https,不仅是基于安全的考虑,有的也是因为第三方平台的限制,如谷歌浏览器会将http站点标记为不安全的站点,微信平台要求接入的微信小程序必须使用https等。 那如何将一个http站点升…...
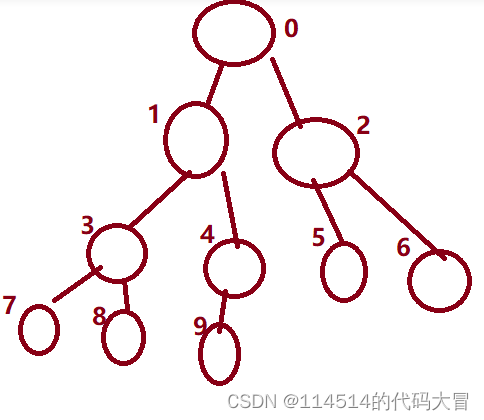
【C语言】数据结构-二叉树
主页:114514的代码大冒险 qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ ) Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 引入 我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树 树是一种非线性的…...

c++中std::condition_variable最全用法归纳
前言 建议阅读以下文章前需先对建立 std::thread 多线程与std::mutex 锁有一定程度的熟悉 std::thread最全用法归纳 std::mutex最全用法归纳 概括 使用 std::condition_variable 的 wait 会把目前的线程 thread 停下来并且等候事件通知,而在另一个线程中可以使用…...

Python数据可视化:数据关系图表可视化
目录 1、散点图 1.1、趋势显示的二维散点图 1.2、分布显示的二维散点图 1.3、散点曲线图...

基于全志D1s的Yuzuki RV Router:带屏旁路由的硬件设计与千兆网络、MIPI屏幕集成方案
基于全志D1s的Yuzuki RV Router:带屏旁路由的硬件设计与千兆网络、MIPI屏幕集成方案 最近在捣鼓智能家居网关,发现市面上的成品要么功能单一,要么价格感人。于是,我把目光投向了开源硬件,想自己动手攒一个。这不&#…...

,电梯程序.基于西门子1200系列两部十层电梯全网最牛逼仿真,博图V15及以上版本,自己编写的...
,电梯程序.基于西门子1200系列两部十层电梯全网最牛逼仿真,博图V15及以上版本,自己编写的,带群控,有超载、故障检修、紧急报警功能,一组外呼按钮,清单有plc组态画面,点表,…...

基于二阶锥规划的配电网重构多时段动态最优潮流研究与应用实例分析
cplex配电网重构多时段,二阶锥规划 参考文献名:主动配电网最优潮流研究及其应用实例(中国电机工程学报) 最优潮流研究在配电网规划运行中不可或缺 ,且在大量分布式能源接入的主动配电网环境下尤 为重要 。 传统 的启发…...

ESP32开发:Ubuntu22.04下ESP-IDF环境一键配置与避坑指南
1. 为什么选择Ubuntu 22.04与ESP-IDF? 如果你刚拿到一块ESP32开发板,摩拳擦掌想搞点物联网项目,第一道坎往往就是搭建开发环境。我见过太多朋友,包括我自己,在环境配置这一步就被劝退了,不是下载慢如蜗牛&a…...

Transformer在图像超分中的革新:从全局建模到纹理迁移
1. 从“近视眼”到“千里眼”:为什么图像超分需要Transformer? 如果你玩过手机拍照,肯定遇到过这种情况:一张特别有纪念意义的照片,因为当时光线不好或者离得太远,拍出来又小又模糊。你想把它放大、修清晰&…...

超低功耗热释电小夜灯硬件设计与实现
1. 项目概述热红外感应低功耗小夜灯是一款面向家庭与住宅场景的自主式环境照明装置,其核心设计目标是实现超长续航、多模式安装适配与人本化光响应。该系统不依赖外部供电网络,采用可更换式锂离子电池供电,典型工况下单次充电可持续运行≥3个…...

Cogito-V1-Preview-Llama-3B效果对比:传统Agent与基于大模型的智能体
Cogito-V1-Preview-Llama-3B效果对比:传统Agent与基于大模型的智能体 最近在折腾智能体项目,发现一个挺有意思的现象:很多人一提到“Agent”,脑子里蹦出来的还是那些写满if-else的规则脚本,或者需要手动配置一大堆流程…...

MiniCPM-V-2_6应用案例:智能识图助手,工作学习效率翻倍
MiniCPM-V-2_6应用案例:智能识图助手,工作学习效率翻倍 1. 引言:当你的电脑能“看懂”图片 想象一下这个场景:你正在写一份报告,需要从一份PDF扫描件里提取表格数据,或者从一张复杂的流程图里总结关键步骤…...

Realistic Vision V5.1本地化部署教程:纯离线、零网络依赖、宽屏交互界面搭建
Realistic Vision V5.1本地化部署教程:纯离线、零网络依赖、宽屏交互界面搭建 想在自己的电脑上体验媲美单反相机的人像摄影效果,但又担心复杂的云端配置和网络依赖?今天,我们就来手把手教你,如何将顶级的Realistic V…...

3步解决Navicat密码遗忘难题:开源解密工具全流程使用指南
3步解决Navicat密码遗忘难题:开源解密工具全流程使用指南 【免费下载链接】navicat_password_decrypt 忘记navicat密码时,此工具可以帮您查看密码 项目地址: https://gitcode.com/gh_mirrors/na/navicat_password_decrypt 数据库管理工作中,忘记N…...
