结合Boosting理论与深度ResNet:ICML2018论文代码详解与实现
代码见:JordanAsh/boostresnet: A PyTorch implementation of BoostResNet
原始论文:Huang F, Ash J, Langford J, et al. Learning deep resnet blocks sequentially using boosting theory[C]//International Conference on Machine Learning. PMLR, 2018: 2058-2067.
算法 1 BoostResNet:用于二分类的收缩和提升
计算 γ ~ t + 1 \tilde{\gamma}_{t+1} γ~t+1
1. 公式对应的算法步骤
在算法 1 中, γ ~ t + 1 \tilde{\gamma}_{t+1} γ~t+1 的计算公式是:
γ ~ t + 1 ← E i ∼ D t [ y i o t + 1 ( x i ) ] \tilde{\gamma}_{t+1} \leftarrow \mathbb{E}_{i \sim D_t} [y_i o_{t+1}(x_i)] γ~t+1←Ei∼Dt[yiot+1(xi)]
代码中,gamma_current 的计算与算法 1 中的 γ ~ t + 1 \tilde{\gamma}_{t+1} γ~t+1 对应。通过将模型输出 Xoutput 与代价 cost 相结合,计算出加权误差,并进行归一化处理,达到与数学期望相似的效果。
2. 计算公式
gamma_current 的计算公式如下:
gamma_current = -1 * np.sum(Xoutput * cost) / Z
数学原理
公式 γ current = − ∑ Xoutput ⋅ cost Z \gamma_{\text{current}} = -\frac{\sum \text{Xoutput} \cdot \text{cost}}{Z} γcurrent=−Z∑Xoutput⋅cost 用于评估模型在训练数据上的表现,结合模型输出与样本代价计算加权误差,并通过归一化处理得到整体误差。其目的是衡量当前模型的预测能力和效果。
- Xoutput 对应 o t + 1 ( x ) o_{t+1}(x) ot+1(x):表示模型在当前阶段的输出。
- cost 替代 y i y_i yi:表示样本的代价函数,用于加权模型输出。虽然在计算中没有显式地显示 y i y_i yi ,但是代价函数本身已经考虑了类别标签 Ytrain[i] 的影响。
- Z:是总代价和,用于归一化处理。
3. 解释公式的各个部分
Xoutput 的含义
- 定义:
Xoutput是模型在训练数据Xtrain上的输出结果矩阵,表示每个样本在各个类别上的预测分数。 - 来源:通过
getPerformance函数计算得到。 - 作用:用于评估模型在当前阶段的预测结果。
accTrain, Xoutput = getPerformance(modelTmp, Xtrain, Ytrain, n)# 模型评估函数
def getPerformance(net, X, Y, n):acc = 0.model.eval()Xoutput = np.zeros((X.shape[0], 10))for batch in range(int(X.shape[0] / opt.batchSize)):start = batch * opt.batchSizestop = (batch + 1) * opt.batchSize - 1ints = np.linspace(start, stop, opt.batchSize).astype(int)data = Variable(torch.from_numpy(X[ints])).float().cuda()for i in range(n):data = allBlocks[i](data)output = net(data)acc += np.mean(torch.max(output, 1)[1].cpu().data.numpy() == Y[ints])Xoutput[ints] = output.cpu().data.numpy()acc /= (X.shape[0] / opt.batchSize)model.train()return acc, Xoutput
cost 的含义
- 定义:
cost是一个矩阵,表示每个样本对每个类别的代价。 - 计算方式:
- 对于非真实类别的代价,计算公式为 exp ( s [ i ] [ l ] − s [ i ] [ Ytrain [ i ] ] ) \exp(s[i][l] - s[i][\text{Ytrain}[i]]) exp(s[i][l]−s[i][Ytrain[i]])。
- 对于真实类别的代价,计算公式为 − ∑ l ≠ Ytrain [ i ] exp ( s [ i ] [ l ] − s [ i ] [ Ytrain [ i ] ] ) -\sum_{l \neq \text{Ytrain}[i]} \exp(s[i][l] - s[i][\text{Ytrain}[i]]) −∑l=Ytrain[i]exp(s[i][l]−s[i][Ytrain[i]])。
- 作用:反映模型在不同类别上的预测偏差。
# 代价函数计算
cost = np.zeros((nTrain, numClasses))
for i in range(nTrain):localSum = 0for l in range(numClasses):if l != Ytrain[i]:cost[i][l] = np.exp(s[i][l] - s[i][int(Ytrain[i])])localSum += cost[i][l]cost[i][int(Ytrain[i])] = -1 * localSumZ += localSum
Z 的含义
- 定义:
Z是总代价的累积和,用于归一化处理。 - 计算方式:通过累加每个样本在所有非真实类别上的代价得到。
- 作用:用于归一化整体误差,使计算结果更加平滑和稳定。
计算 γ \gamma γ
gamma = (gamma_current ** 2 - gamma_previous ** 2)/(1 - gamma_previous ** 2) if gamma > 0: gamma = np.sqrt(gamma)else: gamma = -1 * np.sqrt(-1 * gamma)
为什么这样处理负数的情况?
在步骤3.2中, γ t \gamma_t γt 的计算涉及到 γ ~ t + 1 2 − γ ~ t 2 \tilde{\gamma}_{t+1}^2 - \tilde{\gamma}t^2 γ~t+12−γ~t2 的差值。当这个差值为负时, γ ~ t + 1 2 − γ ~ t 2 1 − γ ~ t 2 \sqrt{\frac{\tilde{\gamma}{t+1}^2 - \tilde{\gamma}_t^2}{1 - \tilde{\gamma}_t^2}} 1−γ~t2γ~t+12−γ~t2 将会产生一个虚数,这在实际计算中是不合适的。
为了避免这种情况,代码中的处理方式是先 将负数取绝对值再开方 ,并在结果前加上 负号 。这确保了计算结果为实数,同时保持了 γ \gamma γ 的实际物理意义。这种处理方式有效地解决了 γ \gamma γ 可能为负数的问题,使得算法能够顺利进行迭代。
这样处理后, γ \gamma γ 的计算既能反映 γ ~ t + 1 2 − γ ~ t 2 \tilde{\gamma}_{t+1}^2 - \tilde{\gamma}_t^2 γ~t+12−γ~t2 的实际变化,又避免了数学上无法接受的情况,确保了算法的稳定性和可行性。
更新 D t + 1 ( i ) D_{t+1}(i) Dt+1(i)
在代码中,更新 D t + 1 ( i ) D_{t+1}(i) Dt+1(i) 的过程与计算损失和权重更新密切相关:
-
计算梯度:
- 使用当前批次的训练数据计算损失
loss。 - 调用
loss.backward()执行反向传播计算梯度。
- 使用当前批次的训练数据计算损失
-
更新权重:
- 执行梯度裁剪
for p in modelTmp.parameters(): p.grad.data.clamp_(-.1, .1)。 - 调用
optimizer.step()进行优化器更新,调整模型参数。
- 执行梯度裁剪
然而,代码中并未明确显示 D t + 1 ( i ) D_{t+1}(i) Dt+1(i) 的更新过程。我们可以假设 optimizer.step() 更新模型参数后,会隐式地影响 D t + 1 ( i ) D_{t+1}(i) Dt+1(i)。
对应于公式的代码实现如下:
# 获取一批训练样本
ints = np.random.random_integers(np.shape(Xtrain)[0] - 1, size=(opt.batchSize))
Xbatch = Xtrain[ints]
Ybatch = Variable(torch.from_numpy(Ytrain[ints])).cuda().long()# 数据变换
if opt.transform: Xbatch = transform(Xbatch)
data = Variable(torch.from_numpy(Xbatch)).float().cuda()
for i in range(n): data = allBlocks[i](data) # 通过多个ResNet块# 获取梯度
output = modelTmp(data)
loss = torch.exp(criterion(output, Ybatch)) # 计算损失
loss.backward() # 反向传播计算梯度# 梯度裁剪
for p in modelTmp.parameters(): p.grad.data.clamp_(-.1, .1)# 优化器更新
optimizer.step() # 优化器更新
虽然代码中没有显式地显示 D t + 1 ( i ) D_{t+1}(i) Dt+1(i) 的更新,但通过优化器更新模型参数,这些参数会影响 D t + 1 ( i ) D_{t+1}(i) Dt+1(i) 的计算和更新过程。
通过这些步骤,代码实现了对 o t + 1 ( x ) o_{t+1}(x) ot+1(x)、 α t + 1 \alpha_{t+1} αt+1 和 w t + 1 w_{t+1} wt+1 的更新,确保了模型在每次迭代中不断优化。
算法 2 BoostResNet:用于训练 ResNet 块的实现

算法2:BoostResNet是用于训练ResNet块的实现。以下是具体步骤及代码的解释:
输入:
- g t ( x ) g_t(x) gt(x): 当前模型的输出
- D t D_t Dt: 当前样本权重
- o t ( x ) o_t(x) ot(x): 当前阶段的输出
- α t \alpha_t αt: 当前阶段的系数
输出:
- f t ( ⋅ ) f_t(\cdot) ft(⋅): 当前阶段的残差块
- α t + 1 \alpha_{t+1} αt+1: 下一个阶段的系数
- w t + 1 w_{t+1} wt+1: 下一个阶段的权重
- o t + 1 ( x ) o_{t+1}(x) ot+1(x): 下一个阶段的输出
算法步骤:
- ( f t , α t + 1 , w t + 1 ) ← arg min ( f , α , v ) ∑ i = 1 m D t ( i ) exp ( − y i α v ⊤ [ f ( g t ( x i ) ) + g t ( x i ) ] + y i α t o t ( x i ) ) (f_t, \alpha_{t+1}, w_{t+1}) \leftarrow \arg\min_{(f, \alpha, v)} \sum_{i=1}^m D_t(i) \exp \left(-y_i \alpha v^{\top} [f(g_t(x_i)) + g_t(x_i)] + y_i \alpha_t o_t(x_i)\right) (ft,αt+1,wt+1)←argmin(f,α,v)∑i=1mDt(i)exp(−yiαv⊤[f(gt(xi))+gt(xi)]+yiαtot(xi))
- o t + 1 ( x ) ← w t + 1 ⊤ [ f t ( g t ( x ) ) + g t ( x ) ] o_{t+1}(x) \leftarrow w_{t+1}^{\top} [f_t(g_t(x)) + g_t(x)] ot+1(x)←wt+1⊤[ft(gt(x))+gt(x)]
结合算法描述解释代码
for batch in range(1, opt.checkEvery+1):optimizer.zero_grad() # 清零梯度# 获取一批训练样本ints = np.random.random_integers(np.shape(Xtrain)[0] - 1, size=(opt.batchSize))Xbatch = Xtrain[ints]Ybatch = Variable(torch.from_numpy(Ytrain[ints])).cuda().long()# 数据变换if opt.transform: Xbatch = transform(Xbatch)data = Variable(torch.from_numpy(Xbatch)).float().cuda()for i in range(n): data = allBlocks[i](data)# 获取梯度output = modelTmp(data)loss = torch.exp(criterion(output, Ybatch))loss.backward()err += loss.data[0]# 评估训练准确率output = modelTmp(data)accTrain += np.mean(torch.max(output, 1)[1].cpu().data.numpy() == Ytrain[ints])# 获取测试准确率model.eval()ints = np.random.random_integers(np.shape(Xtest)[0] - 1, size=(opt.batchSize))Xbatch = Xtest[ints]data = Variable(torch.from_numpy(Xbatch)).float().cuda()for i in range(n): data = allBlocks[i](data)output = modelTmp(data)accTest += np.mean(torch.max(output, 1)[1].cpu().data.numpy() == Ytest[ints])model.train()if batch % opt.printEvery == 0:accTrain /= opt.printEveryaccTest /= opt.printEveryerr /= opt.printEveryprinter([n, rounds, totalIterations + batch + (opt.checkEvery * tries), err, accTrain, accTest])accTrain = 0; accTest = 0; err = 0;for p in modelTmp.parameters(): p.grad.data.clamp_(-.1, .1)optimizer.step()
解释代码的更新过程
-
清零梯度:
optimizer.zero_grad()在每个小批次开始时,优化器会将之前计算的梯度清零,以免累加。
-
获取训练样本:
ints = np.random.random_integers(np.shape(Xtrain)[0] - 1, size=(opt.batchSize)) Xbatch = Xtrain[ints] Ybatch = Variable(torch.from_numpy(Ytrain[ints])).cuda().long()从训练数据中随机抽取一个小批次的样本。
-
数据变换:
if opt.transform: Xbatch = transform(Xbatch) data = Variable(torch.from_numpy(Xbatch)).float().cuda() for i in range(n): data = allBlocks[i](data)如果有数据变换操作,则对数据进行变换。然后,数据通过多个ResNet块进行处理。
-
获取梯度:
output = modelTmp(data) loss = torch.exp(criterion(output, Ybatch)) loss.backward() err += loss.data[0]计算当前模型的输出和损失,然后通过反向传播计算梯度。
-
评估训练准确率:
output = modelTmp(data) accTrain += np.mean(torch.max(output, 1)[1].cpu().data.numpy() == Ytrain[ints])使用当前模型预测并计算训练数据的准确率。
-
获取测试准确率:
model.eval() ints = np.random.random_integers(np.shape(Xtest)[0] - 1, size=(opt.batchSize)) Xbatch = Xtest[ints] data = Variable(torch.from_numpy(Xbatch)).float().cuda() for i in range(n): data = allBlocks[i](data) output = modelTmp(data) accTest += np.mean(torch.max(output, 1)[1].cpu().data.numpy() == Ytest[ints]) model.train()切换到评估模式,使用测试数据计算模型的准确率,然后切换回训练模式。
-
打印训练和测试准确率:
if batch % opt.printEvery == 0:accTrain /= opt.printEveryaccTest /= opt.printEveryerr /= opt.printEveryprinter([n, rounds, totalIterations + batch + (opt.checkEvery * tries), err, accTrain, accTest])accTrain = 0; accTest = 0; err = 0;每隔一段时间打印训练和测试的准确率以及损失。
-
梯度裁剪和优化器更新:
for p in modelTmp.parameters(): p.grad.data.clamp_(-.1, .1) optimizer.step()对梯度进行裁剪,防止梯度爆炸,然后更新模型参数。
结合算法2解释代码更新过程
1. 更新 f t ( ⋅ ) f_t(\cdot) ft(⋅)
f t ( ⋅ ) f_t(\cdot) ft(⋅) 表示当前阶段的残差块模型。在代码中,通过模型的训练过程(包括前向传播和反向传播)来更新 f t ( ⋅ ) f_t(\cdot) ft(⋅)。
for batch in range(1, opt.checkEvery+1):optimizer.zero_grad() # 清零梯度# 获取一批训练样本ints = np.random.random_integers(np.shape(Xtrain)[0] - 1, size=(opt.batchSize))Xbatch = Xtrain[ints]Ybatch = Variable(torch.from_numpy(Ytrain[ints])).cuda().long()# 数据变换if opt.transform: Xbatch = transform(Xbatch)data = Variable(torch.from_numpy(Xbatch)).float().cuda()for i in range(n): data = allBlocks[i](data) # 通过多个ResNet块# 获取梯度output = modelTmp(data)loss = torch.exp(criterion(output, Ybatch)) # 计算损失loss.backward() # 反向传播计算梯度err += loss.data[0]
解释:
- 数据处理和前向传播:
for i in range(n): data = allBlocks[i](data)表示通过多个ResNet块进行前向传播,更新当前阶段的残差块模型 f t ( ⋅ ) f_t(\cdot) ft(⋅),相当于计算 f t ( g t ( x ) ) f_t(g_t(x)) ft(gt(x))。 - 反向传播:
loss.backward()执行反向传播计算梯度,这一步会更新modelTmp和各个残差块allBlocks中的参数。。
2. 更新 α t + 1 \alpha_{t+1} αt+1
α t + 1 \alpha_{t+1} αt+1 表示当前阶段的权重参数。在代码中,通过损失函数和梯度的计算,优化得到新的 α t + 1 \alpha_{t+1} αt+1。
# 获取梯度output = modelTmp(data)loss = torch.exp(criterion(output, Ybatch)) # 计算损失loss.backward() # 反向传播计算梯度err += loss.data[0]
解释:
- 损失函数计算:
loss = torch.exp(criterion(output, Ybatch))使用交叉熵损失函数计算损失,这一步间接影响 α t + 1 \alpha_{t+1} αt+1的更新。 - 反向传播和优化器更新:
loss.backward()和optimizer.step()通过反向传播和优化器更新来调整模型参数,其中包括 α t + 1 \alpha_{t+1} αt+1。
3. 更新 w t + 1 w_{t+1} wt+1
w t + 1 w_{t+1} wt+1 表示当前阶段的权重向量。在代码中,通过模型的反向传播和优化器更新来学习 w t + 1 w_{t+1} wt+1。
# 评估训练准确率output = modelTmp(data)accTrain += np.mean(torch.max(output, 1)[1].cpu().data.numpy() == Ytrain[ints])# 获取测试准确率model.eval()ints = np.random.random_integers(np.shape(Xtest)[0] - 1, size=(opt.batchSize))Xbatch = Xtest[ints]data = Variable(torch.from_numpy(Xbatch)).float().cuda()for i in range(n): data = allBlocks[i](data)output = modelTmp(data)accTest += np.mean(torch.max(output, 1)[1].cpu().data.numpy() == Ytest[ints])model.train()if batch % opt.printEvery == 0:accTrain /= opt.printEveryaccTest /= opt.printEveryerr /= opt.printEveryprinter([n, rounds, totalIterations + batch + (opt.checkEvery * tries), err, accTrain, accTest])accTrain = 0; accTest = 0; err = 0;for p in modelTmp.parameters(): p.grad.data.clamp_(-.1, .1) # 梯度裁剪optimizer.step() # 优化器更新
解释:
- 梯度裁剪:
for p in modelTmp.parameters(): p.grad.data.clamp_(-.1, .1)用于防止梯度爆炸,同时保证 w t + 1 w_{t+1} wt+1的更新。 - 优化器更新:
optimizer.step()通过优化器更新模型参数,其中包括 w t + 1 w_{t+1} wt+1。
总结来说,代码中通过前向传播、反向传播、梯度裁剪和优化器更新的过程来分别更新 f t ( ⋅ ) f_t(\cdot) ft(⋅)、 α t + 1 \alpha_{t+1} αt+1 和 w t + 1 w_{t+1} wt+1。
4 计算 o t + 1 ( x ) o_{t+1}(x) ot+1(x)
在代码中,计算 o t + 1 ( x ) o_{t+1}(x) ot+1(x) 的过程主要通过将数据传递给残差块和模型临时参数 modelTmp 来实现。具体步骤如下:
-
数据前向传播:
- 数据
data通过多个残差块allBlocks[i]进行前向传播。 - 经过残差块处理后的数据传递给
modelTmp,得到输出output。
- 数据
-
计算新的输出 o t + 1 ( x ) o_{t+1}(x) ot+1(x):
- 计算新一轮的输出,即 o t + 1 ( x ) o_{t+1}(x) ot+1(x),通过
modelTmp得到。
- 计算新一轮的输出,即 o t + 1 ( x ) o_{t+1}(x) ot+1(x),通过
代码实现:
for i in range(n): data = allBlocks[i](data) # 通过多个ResNet块
output = modelTmp(data) # 计算新的输出 o_{t+1}(x)
for i in range(n): data = allBlocks[i](data):数据通过多个残差块进行前向传播,得到处理后的数据data。output = modelTmp(data):处理后的数据data传递给modelTmp,得到输出output,即 o t + 1 ( x ) o_{t+1}(x) ot+1(x)。
总结
- f t ( ⋅ ) f_t(\cdot) ft(⋅) 的更新通过前向传播和反向传播实现,通过优化器更新模型参数。
- α t + 1 \alpha_{t+1} αt+1 和 w t + 1 w_{t+1} wt+1 通过损失函数计算和优化器更新实现。
- 这些更新过程都是通过代码中的梯度计算(
loss.backward())和优化器更新步骤(optimizer.step())来完成的。
代码解析及功能实现
这段代码实现了一个训练ResNet块并逐层训练的过程。这个过程结合了Boosting理论,通过逐层训练ResNet块来提高分类性能。
代码前期准备
import torch
import sys
import pickle
import os
import numpy as np
import torchfile
from torch import nn
from torch.autograd import Variable
import argparse
导入了必要的库,包括PyTorch、NumPy、系统操作、数据加载和命令行参数解析库。
解析命令行参数
parser = argparse.ArgumentParser()
parser.add_argument('--gammaFirst', default=0.5, help='initial gamma')
parser.add_argument('--checkEvery', default=10000, help='how frequently to check gamma requirement - 10k for cifar, 5k for svhn')
parser.add_argument('--data', default='SVHN.t7', help='load data')
parser.add_argument('--gammaThresh',default=-0.0001, help='gamma threshold to stop training layer')
parser.add_argument('--lr', default=0.001, help='learning rate')
parser.add_argument('--maxIters', default=10000, help='maximum iterations before stopping train layer')
parser.add_argument("--transform", help='do CIFAR-style image transformations?', action="store_true")
parser.add_argument('--printEvery', default=100, help='how frequently to print')
parser.add_argument('--batchSize', default=100, help='batch size')
parser.add_argument('--modelPath', default='model.pt', help='output model')
opt = parser.parse_args()
解析命令行参数,设置各种训练超参数,包括初始gamma值、检查gamma的频率、数据集路径、gamma阈值、学习率、最大迭代次数、是否进行数据变换、打印频率、批处理大小和模型保存路径。
加载数据
data = torchfile.load(opt.data) # load dataset in torch format (assuming already normalized)
Xtrain = data.Xtrain
Ytrain = data.Ytrain - 1
Xtest = data.Xtest
Ytest = data.Ytest - 1
cut = int(np.shape(Xtrain)[0] / opt.batchSize * opt.batchSize) # cut off a few samples for simplicity
nTrain = cut
Xtrain = Xtrain[:cut]
Ytrain = Ytrain[:cut]
cut = int(np.shape(Xtest)[0] / opt.batchSize * opt.batchSize)
Xtest = Xtest[:cut]
Ytest = Ytest[:cut]
nTest = cut
numClasses = 10
加载并处理数据集,将训练集和测试集按批处理大小进行裁剪,以确保数据大小是批处理大小的整数倍。
定义打印函数
def printer(print_arr):for v in print_arr: sys.stdout.write(str(v) + '\t')sys.stdout.write('\n')sys.stdout.flush()
定义一个打印函数,用于在控制台打印输出。
加载ResNet模型并构建块
import fbrn
model = fbrn.tmp
model.load_state_dict(torch.load('fbrn.pth'))
allBlocks = {}
allBlocks[0] = nn.Sequential(model[0], model[1], model[2])
for i in range(8): allBlocks[1 + i] = model[3][i]
for i in range(8): allBlocks[9 + i] = model[4][i]
for i in range(8): allBlocks[17+ i] = model[5][i]
criterion = nn.CrossEntropyLoss().cuda()
nFilters = 15; rounds = 25
加载预训练的ResNet模型,并将其分成多个块,分别存储在allBlocks字典中。定义损失函数为交叉熵损失。
allBlocks[0]包含model的第 0 层到第 2 层,使用nn.Sequential将这些层组合在一起。for i in range(8): allBlocks[1 + i] = model[3][i]将model的第 3 层的 8 个子层分别存储在allBlocks的索引 1 到 8。for i in range(8): allBlocks[9 + i] = model[4][i]将model的第 4 层的 8 个子层分别存储在allBlocks的索引 9 到 16。for i in range(8): allBlocks[17 + i] = model[5][i]将model的第 5 层的 8 个子层分别存储在allBlocks的索引 17 到 24。
这样,allBlocks 字典就包含了模型的所有层,并且这些层被分割成了不同的块,每个块对应一个连续的索引范围。
分块的意义
这段代码将模型分为了三个主要的残差块(residual blocks):
- 第 0 块:
allBlocks[0]包含模型的第 0 层到第 2 层。 - 第 1 块:
allBlocks[1]到allBlocks[8]包含模型的第 3 层的 8 个子层。 - 第 2 块:
allBlocks[9]到allBlocks[16]包含模型的第 4 层的 8 个子层。 - 第 3 块:
allBlocks[17]到allBlocks[24]包含模型的第 5 层的 8 个子层。
数据增强函数
def transform(X):tmp = np.zeros((np.shape(X)[0], 3, 38, 38))tmp[:, :, 2:34, 2:34] = Xfor i in range(np.shape(X)[0]):r1 = np.random.randint(4)r2 = np.random.randint(4)X[i] = tmp[i, :, r1 : r1 + 32, r2 : r2 + 32]if np.random.uniform() > .5:X[i] = X[i, :, :, ::-1]return X
定义数据增强函数,用于CIFAR样式的图像变换,进行随机裁剪和水平翻转。
模型评估函数
def getPerformance(net, X, Y, n):acc = 0.model.eval()Xoutput = np.zeros((X.shape[0], 10))for batch in range(int(X.shape[0] / opt.batchSize)):start = batch * opt.batchSize; stop = (batch + 1) * opt.batchSize - 1ints = np.linspace(start, stop, opt.batchSize).astype(int)data = Variable(torch.from_numpy(X[ints])).float().cuda()for i in range(n): data = allBlocks[i](data)output = net(data)acc += np.mean(torch.max(output, 1)[1].cpu().data.numpy() == Y[ints])Xoutput[ints] = output.cpu().data.numpy()acc /= (X.shape[0] / opt.batchSize)model.train()return acc, Xoutput
定义模型评估函数,用于在训练和测试数据集上计算模型的准确率。
初始化模型统计数据
a_previous = 0.0
a_current = -1.0
s = np.zeros((nTrain, numClasses))
cost = np.zeros((nTrain, numClasses))
Xoutput_previous = np.zeros((nTrain, numClasses))
Ybatch = np.zeros((opt.batchSize))
YbatchTest = np.zeros((opt.batchSize))
gamma_previous = opt.gammaFirst
totalIterations = 0; tries = 0
初始化一些变量,用于存储模型统计数据、损失、输出和其他辅助数据。
逐层训练模型
for n in range(rounds):gamma = -1Z = 0# create cost function for i in range(nTrain):localSum = 0for l in range(numClasses):if l != Ytrain[i]:cost[i][l] = np.exp(s[i][l] - s[i][int(Ytrain[i])])localSum += cost[i][l]cost[i][int(Ytrain[i])] = -1 * localSumZ += localSum# fetch the correct classification layersbk = allBlocks[n]ci = nn.Sequential(model[6], model[7], model[8])if n < 17: ci = nn.Sequential(allBlocks[17], ci)if n < 9: ci = nn.Sequential(allBlocks[9], ci)modelTmp = nn.Sequential(bk, ci, nn.Softmax(dim=0))modelTmp = modelTmp.cuda()optimizer = torch.optim.Adam(modelTmp.parameters(), lr=opt.lr) tries = 0XbatchTest = torch.zeros(opt.batchSize, nFilters, 32, 32)while (gamma < opt.gammaThresh and ((opt.checkEvery * tries) < opt.maxIters)):accTrain = 0; accTest = 0; err = 0;for batch in range(1, opt.checkEvery + 1):optimizer.zero_grad()# get batch of training samplesints = np.random.random_integers(np.shape(Xtrain)[0] - 1, size=(opt.batchSize))Xbatch = Xtrain[ints]Ybatch = Variable(torch.from_numpy(Ytrain[ints])).cuda().long()# do transformationsif opt.transform: Xbatch = transform(Xbatch)data = Variable(torch.from_numpy(Xbatch)).float().cuda()for i in range(n): data = allBlocks[i](data)# get gradientsoutput = modelTmp(data)loss = torch.exp(criterion(output, Ybatch))loss.backward()err += loss.data[0]# evaluate training accuracyoutput = modelTmp(data)accTrain += np.mean(torch.max(output, 1)[1].cpu().data.numpy() == Ytrain[ints])# get test accuracy model.eval()ints = np.random.random_integers(np.shape(Xtest)[0] - 1, size=(opt.batchSize))Xbatch = Xtest[ints]data = Variable(torch.from_numpy(Xbatch)).float().cuda()for i in range(n): data = allBlocks[i](data)output = modelTmp(data)accTest += np.mean(torch.max(output, 1)[1].cpu().data.numpy() == Ytest[ints])model.train()if batch % opt.printEvery == 0:accTrain /= opt.printEveryaccTest /= opt.printEveryerr /= opt.printEveryprinter([n, rounds, totalIterations + batch + (opt.checkEvery * tries), err, accTrain, accTest])accTrain = 0;accTest = 0; err = 0;optimizer.step()totalIterations += opt.checkEverytries += 1# get performance of new layera_current, Xoutput_previous = getPerformance(modelTmp, Xtrain, Ytrain, n + 1)gamma = (a_current - a_previous) / (1 - a_current)a_previous = a_currentprinter([n, gamma, opt.gammaThresh])if gamma < opt.gammaThresh:breakelse:s += np.log(Xoutput_previous)
逐层训练ResNet块,使用Boosting理论来增强分类性能。具体步骤包括:
- 计算损失函数。
- 加载对应的ResNet块。
- 进行优化迭代,计算训练和测试集上的准确率,并根据gamma值判断是否继续训练。
保存模型
torch.save(model.state_dict(), opt.modelPath)
保存训练好的模型。
核心代码
初始化部分
a_previous = 0.0
a_current = -1.0
s = np.zeros((nTrain, numClasses))
cost = np.zeros((nTrain, numClasses))
Xoutput_previous = np.zeros((nTrain, numClasses))
Ybatch = np.zeros((opt.batchSize))
YbatchTest = np.zeros((opt.batchSize))
gamma_previous = opt.gammaFirst
totalIterations = 0; tries = 0
这里初始化了一些变量,包括模型的统计信息、训练样本的预测输出、批量训练样本等。其中:
a_previous和a_current是当前和之前的提升系数。s是一个保存每个训练样本在每个类别上的累积输出。cost是样本的代价矩阵。Xoutput_previous是上一轮的输出。gamma_previous是上一轮的提升系数。totalIterations和tries用于记录总迭代次数和尝试次数。
1.初始化阶段(主循环)
for n in range(rounds):gamma = -1Z = 0
gamma = -1和Z = 0初始化了一些用于计算的变量。rounds是算法的迭代轮数。在代码中设置为25,每轮迭代都会添加一个新的残差块,并调整模型参数。- 每一轮次训练前将
gamma和Z置零。
2.计算代价函数
for i in range(nTrain):localSum = 0for l in range(numClasses):if l != Ytrain[i]:cost[i][l] = np.exp(s[i][l] - s[i][int(Ytrain[i])])localSum += cost[i][l]cost[i][int(Ytrain[i])] = -1 * localSumZ += localSum
这个部分计算每个训练样本的代价函数,并将计算所有错误分类的代价,存储在 cost 数组中。
每个训练样本的成本通过计算每个类别的错误分类代价 cost。如果样本 i 的真实类别为 Ytrain[i],则计算该样本在其他类别上的成本之和 localSum,并将 localSum 赋值给该样本真实类别的成本(取负值)。
cost[i][l] = np.exp(s[i][l] - s[i][int(Ytrain[i])])计算样本 i i i 在类别 l l l 上的代价。cost[i][int(Ytrain[i])] = -1 * localSum将当前样本在其真实类别上的代价设为负的localSum。Z是所有样本的总代价。
3. 获取当前分类层
bk = allBlocks[n]ci = nn.Sequential(model[6], model[7], model[8])if n < 17: ci = nn.Sequential(allBlocks[17], ci)if n < 9: ci = nn.Sequential(allBlocks[9], ci)modelTmp = nn.Sequential(bk, ci, nn.Softmax(dim=0))modelTmp = modelTmp.cuda()
这段代码的作用是创建一个临时模型 modelTmp,它由当前迭代的残差块 bk 和一些预定义的分类层 ci 组成。以下是具体解释:
bk表示当前迭代的残差块。ci表示后续的分类层,包含模型中的一些层。
根据当前迭代次数 n,动态调整 ci 的层次结构:
- 如果当前迭代次数
n小于 17,那么在分类层ci前面加上第 17 块的残差块。 - 如果当前迭代次数
n小于 9,那么在分类层ci前面加上第 9 块的残差块。
这样的设计使得模型在不同的迭代次数 n 下,分类层 ci 的结构不同,逐步增加模型的复杂性。这个结构确保了模型能够逐层学习和调整,从而提高分类性能。
4.1 优化器设置
optimizer = torch.optim.Adam(modelTmp.parameters(), lr=opt.lr) tries = 0XbatchTest = torch.zeros(opt.batchSize, nFilters, 32, 32)
使用 Adam 优化器,并初始化 XbatchTest 用于测试。
Adam 优化器是什么?大概的数学原理是什么?是对应的梯度下降算法吗?还是什么其他的算法?
Adam(Adaptive Moment Estimation)是一种基于一阶梯度的优化算法,结合了动量和自适应学习率两个方法。它在深度学习中被广泛使用,因为它在处理稀疏梯度和非平稳目标上表现良好。
Adam的数学原理:
- 计算每个参数的梯度的一阶动量(平均值)和二阶动量(方差)。
- 对每个参数的更新使用动量和学习率的校正。
具体来说,Adam 优化器的步骤如下:
- 初始化动量和二阶动量。
- 在每次迭代中更新动量和二阶动量。
- 根据动量和二阶动量校正参数更新步长。
具体的更新公式为:
- m t = β 1 m t − 1 + ( 1 − β 1 ) g t m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t mt=β1mt−1+(1−β1)gt
- v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 vt=β2vt−1+(1−β2)gt2
- m ^ t = m t 1 − β 1 t \hat{m}_t = \frac{m_t}{1 - \beta_1^t} m^t=1−β1tmt
- v ^ t = v t 1 − β 2 t \hat{v}_t = \frac{v_t}{1 - \beta_2^t} v^t=1−β2tvt
- θ t = θ t − 1 − η m ^ t v ^ t + ϵ \theta_t = \theta_{t-1} - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} θt=θt−1−ηv^t+ϵm^t
其中:
- g t g_t gt 是梯度。
- m t m_t mt 和 v t v_t vt 分别是一阶和二阶动量。
- β 1 \beta_1 β1 和 β 2 \beta_2 β2 是动量系数,通常取 0.9 0.9 0.9 和 0.999 0.999 0.999。
- ϵ \epsilon ϵ 是一个小常数,用于防止分母为零,通常取 1 0 − 8 10^{-8} 10−8。
- η \eta η 是学习率。
4.2 训练循环

while (gamma < opt.gammaThresh and ((opt.checkEvery * tries) < opt.maxIters)):accTrain = 0; accTest = 0; err = 0;for batch in range(1, opt.checkEvery+1):optimizer.zero_grad()
zero_grad():在每次反向传播之前,将所有参数的梯度缓存清零。在 PyTorch 中,梯度是累加的,所以需要在每次迭代开始前清零。
在满足 gamma 小于阈值和最大迭代次数限制的条件下,开始训练循环。
关于 opt.gammaThresh 和 gamma
这里的 opt.gammaThresh 对应算法中的 γ t \gamma_t γt,而 gamma 对应的是 γ \gamma γ。代码中的逻辑 while (gamma < opt.gammaThresh) 实际上在检查当前的 γ \gamma γ 是否小于阈值。这是因为我们希望 γ \gamma γ 足够大,代表模型的分类能力足够强,当 γ \gamma γ 小于阈值时,停止训练。
具体来说:
gamma初始化为 -1,表示最差情况。- 当训练时,更新
gamma的值,如果gamma达到或超过opt.gammaThresh,则说明模型性能达到预期,可以停止训练。
获取训练样本批次
ints = np.random.random_integers(np.shape(Xtrain)[0] - 1, size=(opt.batchSize))Xbatch = Xtrain[ints]Ybatch = Variable(torch.from_numpy(Ytrain[ints])).cuda().long()
从训练集中随机选择一个批次样本,并将其转换为 PyTorch 变量。
数据变换和前向传播
if opt.transform: Xbatch = transform(Xbatch)data = Variable(torch.from_numpy(Xbatch)).float().cuda()for i in range(n): data = allBlocks[i](data)
如果指定了数据变换,则对数据进行变换,然后进行前向传播,通过前 n 个残差块处理数据。
获取梯度和更新权重
output = modelTmp(data)loss = torch.exp(criterion(output, Ybatch))loss.backward()err += loss.data[0]output = modelTmp(data)accTrain += np.mean(torch.max(output,1)[1].cpu().data.numpy() == Ytrain[ints])model.eval()ints = np.random.random_integers(np.shape(Xtest)[0] - 1, size=(opt.batchSize))Xbatch = Xtest[ints]data = Variable(torch.from_numpy(Xbatch)).float().cuda()for i in range(n): data = allBlocks[i](data)output = modelTmp(data)accTest += np.mean(torch.max(output,1)[1].cpu().data.numpy() == Ytest[ints])model.train()
在训练过程中,通过交叉熵+指数损失函数计算并累积损失 err
criterion = nn.CrossEntropyLoss().cuda()
计算训练准确率 accTrain 和测试准确率 accTest。
打印和梯度裁剪
if batch % opt.printEvery == 0:accTrain /= opt.printEveryaccTest /= opt.printEveryerr /= opt.printEveryprinter([n, rounds, totalIterations + batch + (opt.checkEvery * tries), err, accTrain, accTest])accTrain = 0; accTest = 0; err = 0;for p in modelTmp.parameters(): p.grad.data.clamp_(-.1, .1) optimizer.step()
- 每隔
opt.printEvery次批量训练输出一次当前状态,包括错误率、训练准确率和测试准确率。 - 进行梯度裁剪,防止梯度爆炸。
step():执行一步优化算法,即根据当前的梯度和动量更新模型参数。
梯度裁剪对应的代码是:
for p in modelTmp.parameters(): p.grad.data.clamp_(-.1, .1)
这段代码通过限制梯度的值在 [-0.1, 0.1] 范围内,防止梯度爆炸。这对于稳定训练过程非常重要,尤其是深度神经网络,梯度可能会在反向传播过程中变得非常大。
计算 gamma 值
accTrain, Xoutput = getPerformance(modelTmp, Xtrain, Ytrain, n)gamma_current = -1 * np.sum(Xoutput * cost) / Zgamma = (gamma_current ** 2 - gamma_previous ** 2)/(1 - gamma_previous ** 2) if gamma > 0: gamma = np.sqrt(gamma)else: gamma = -1 * np.sqrt(-1 * gamma)a_current = 0.5 * np.log((1 + gamma_current) / (1 - gamma_current))
更新模型参数,并在每个批量训练后进行一次梯度下降。
- 计算当前模型的性能,得到
gamma_current。 - 根据
gamma_current和gamma_previous更新gamma。
公式:
γ t ← γ ~ t + 1 2 − γ ~ t 2 1 − γ ~ t 2 \gamma_t \leftarrow \sqrt{\frac{\tilde{\gamma}_{t+1}^2 - \tilde{\gamma}_t^2}{1 - \tilde{\gamma}_t^2}} γt←1−γ~t2γ~t+12−γ~t2
其中:
gamma_current是当前训练轮次的 γ t \gamma_t γt。gamma_previous是前一次训练轮次的 γ t \gamma_t γt。
为什么这样处理负数的情况?
当 γ \gamma γ 为负数时,我们使用以下公式进行更新:
γ = − 1 ∗ − 1 ∗ γ ~ t + 1 2 − γ ~ t 2 1 − γ ~ t 2 \gamma = -1 * \sqrt{-1 * \frac{\tilde{\gamma}_{t+1}^2 - \tilde{\gamma}_t^2}{1 - \tilde{\gamma}_t^2}} γ=−1∗−1∗1−γ~t2γ~t+12−γ~t2
这样处理的原因是:
- γ \gamma γ 的计算可能会因为 γ ~ t + 1 2 − γ ~ t 2 \tilde{\gamma}_{t+1}^2 - \tilde{\gamma}_t^2 γ~t+12−γ~t2 的值而导致根号内出现负数。这在数学上是不可接受的。
- 为了避免这种情况,取负号后再开方,以确保 γ \gamma γ 的计算结果是一个实数。负号处理后仍然保持 γ \gamma γ 的真实值,因为 γ \gamma γ 本身可以是负数或正数。
这个处理方式巧妙地避免了计算过程中根号内为负数的问题,同时保持了 γ \gamma γ 的实际含义。
尝试次数和权重更新
tries += 1if (gamma > opt.gammaThresh or ((opt.checkEvery * tries) >= opt.maxIters)):totalIterations = totalIterations + (tries * opt.checkEvery)printer([gamma, gamma_current, gamma_previous])printer(['a_{t+1}:', a_current, 'gamma_t:', gamma]) s += Xoutput * a_current - Xoutput_previous * a_previousaccTest, _ = getPerformance(modelTmp, Xtest, Ytest, n) printer(['t', rounds, 'numBatches:', tries * opt.checkEvery, 'test accuracy:', accTest]) gamma_previous = gamma_current
更新 tries,如果 gamma 达到阈值或尝试次数达到最大迭代次数,则记录迭代次数并打印信息。最后更新累积输出 s 和 gamma_previous。
相关文章:

结合Boosting理论与深度ResNet:ICML2018论文代码详解与实现
代码见:JordanAsh/boostresnet: A PyTorch implementation of BoostResNet 原始论文:Huang F, Ash J, Langford J, et al. Learning deep resnet blocks sequentially using boosting theory[C]//International Conference on Machine Learning. PMLR, 2…...

Python使用策略模式绘制图片分析多组数据
趋势分析:折线图静态比较:条形图分布分析:箱线图离散情况:散点图 import matplotlib.pylab as plt from abc import ABC, abstractmethod import seaborn as sns import pandas as pd import plotly.graph_objects as go import p…...
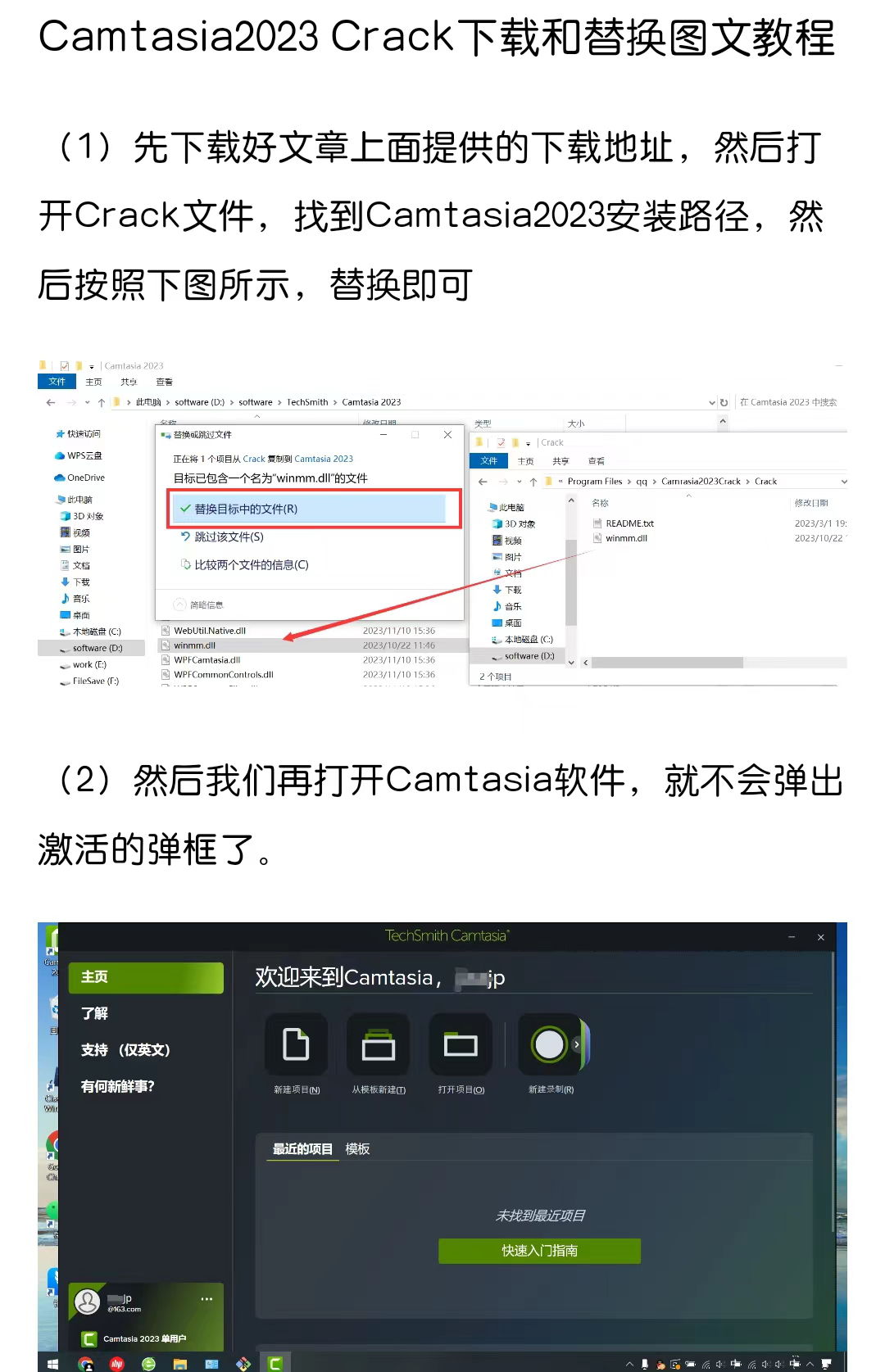
【软件下载】Camtasia Studio 2024详细安装教程视频
习惯上来说Camtasia Studio是一款简单易用的高清录屏和视频编辑软件,拥有录制屏幕和配音、视频的剪辑和过场动画片、添加说明字幕和水印、制作视频封面和菜单、视频压缩和播放。不得不说Camtasia是一款屏幕录制和视频剪辑软件,教授课程,培训他…...
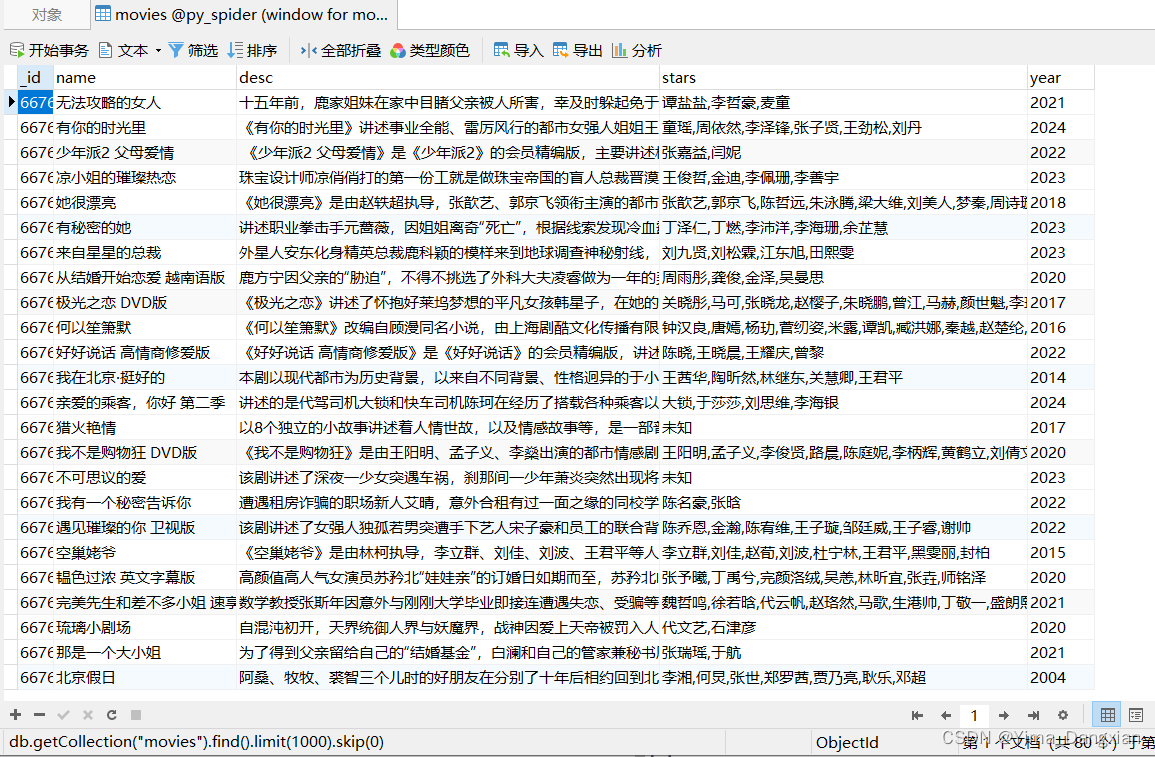
爬虫笔记15——爬取网页数据并使用redis数据库set类型去重存入,以爬取芒果踢V为例
下载redis数据库 首先需要下载redis数据库,可以直接去Redis官网下载。或者可以看这里下载过程。 pycharm项目文件下载redis库 > pip install redis 然后在程序中连接redis服务: from redis import RedisredisObj Redis(host127.0.0.1, port6379)…...
我是如何在markdown编辑器中完成视频的插入和播放的
如果你有更好用的编辑器组件,请一定推荐给我!!!(最好附带使用说明🤓️) 介绍 在开发一个社区页面的时候,需要完成发帖、浏览帖子的能力。这里考虑接入markdown编辑器进行开发,也符合大多数用户的习惯。 …...
Ltv 数据粘包处理
测试数据包的生成 校验程序处理结果和原始的日志保温解析是否一致 程序粘包分解正常...
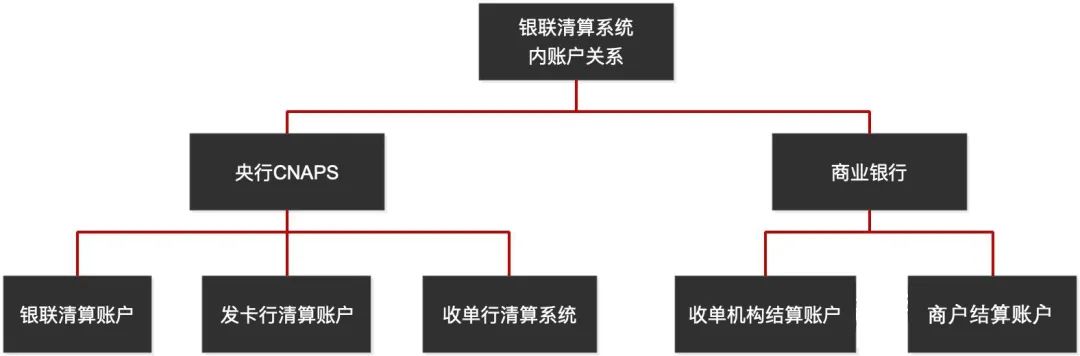
银联支付,你竟然还不知道它怎么工作?
银联支付咱都用过,微信和支付宝没这么“横行”的时侯,我们取款、转账、付款时用的ATM机、POS机,都是银联支付完成的。 今天,就让咱们了解一下银行卡支付的工作原型。 首先,说说中国银联 中国银联(China U…...

查找程序中隐藏界面的思路
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动 某些程序,它会有管理员界面(比如棋牌游戏,它一般会有一个控制端界面,用来控制发牌、换牌),但是这种界…...

umount
umount命令用于卸载文件系统,使得挂载点的文件和目录变为不可访问。 基本用法: umount [选项] 设备或文件夹 常见选项: -f:强制卸载,即使文件系统处于忙碌状态(在某些情况下使用,如网络文件…...

electron录制应用-自由画板功能
功能 录屏过程中的涂画功能允许用户在录制屏幕操作的同时,实时添加注释和高亮显示,以增强信息的传达和观众的理解。 效果 electron录制-添加画布 代码实现 1、利用HTML5的Canvas元素实现一个自由涂画的功能,允许用户在网页上进行手绘创作。…...

版本控制工具-git分支管理
目录 前言一、git分支管理基本命令1.1 基本命令2.1 实例 二、git分支合并冲突解决三、git merge命令与git rebase命令对比 前言 本篇文章介绍git分支管理的基本命令,并说明如何解决git分支合并冲突,最后说明git merge命令与git rebase命令的区别。 一、…...
医卫医学试题及答案,分享几个实用搜题和学习工具 #学习方法#知识分享#经验分享
可以说是搜题软件里面题库较为齐全的一个了,收录国内高校常见的计算机类、资格类、学历类、外语类、工程类、建筑类等多种类型的题目。它可以拍照解题、拍照答疑、智能解题,并支持每日一练、章节练习、错题重做等特色功能,在帮助大家解答疑惑…...

在dolphinDB上直接保存一个dataframe为分布式数据表
步骤1:获取链接 import dolphindb as ddb from loguru import loggerdef get_dolphin_session():"""获取dolphinDB的session"""dolphin_config {"host": "127.0.0.1","port": 13900,"username&…...

awk
awk grep 查 sed 增删改查 awk 按行取列 awk默认分割符: 空格;tab键。多个空格压缩成一个空格 [roottest2 opt]# cat awk.txt 1 2 3 [roottest2 opt]# awk {print $3} awk.txt 3 awk的工作原理: 根据指令信息,逐行的读…...

如何加速AI原生应用进程?华为云开天aPaaS提出新范式
每一次新旧代际转换时,都会上演这样的一幕:“畅想很多,落地很少”,AI原生应用似乎也不例外。 关于AI原生应用的呼声已经持续一段时间,但普通用户对“AI原生”依然陌生。除了新业态普及的周期性,AI原生应用…...

Matlab基础语法:变量和数据类型,基本运算,矩阵和向量,常用函数,脚本文件
目录 一、变量和数据类型 二、基本运算 三、矩阵和向量 四、常用函数 五、脚本文件 六、总结 一、变量和数据类型 Matlab 支持多种数据类型,包括数值类型、字符类型和逻辑类型。掌握这些基本的变量和数据类型,是我们进行数学建模和计算的基础。 数…...
弥补iPhone不足,推荐金鸣识别等几款APP神器
在数字时代的浪潮中,iPhone以其独特的设计和强大的性能赢得了全球众多用户的喜爱。然而,即便是这样一款近乎完美的设备,也难免存在一些局限性和缺陷。幸运的是,App Store中蕴藏着许多鲜为人知的app,它们可以弥补iPhone…...

KLayout 中的默认数据类型
KLayout 中的默认数据类型 这里给大家介绍一下 KLayout 中的默认数据类型。从这个官方文档 KLayout 数据类型 中我们可以获取到 KLayout 中的默认数据类型有如下几种: Column 1Column 2TypeBoolean布尔值TypeCallback按键返回类型TypeDouble浮点数类型TypeInt整型Ty…...

视频云存储平台LntonCVS国标视频平台功能和应用场景详细介绍
LntonCVS国标视频融合云平台基于先进的端-边-云一体化架构设计,以轻便的部署和灵活多样的功能为特点。该平台不仅支持多种通信协议如GB28181、RTSP、Onvif、海康SDK、Ehome、大华SDK、RTMP推流等,还能兼容各类设备,包括IPC、NVR和监控平台。在…...

C语言 将程序第4,5行改为 c1=197;c2=198;将程序第3行改为int c1,c2;
问题代码如下: #include<stdio.h> int main() { char c1,c2; c197; c298; printf(“c1%c,c2%c\n”,c1,c2); printf(“c1%d,c2%d\n”,c1,c2); return 0; } 运行时会输出什么信息?为什么?如果将程序第4&am…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
