深度神经网络——决策树的实现与剪枝
概述
决策树 是一种有用的机器学习算法,用于回归和分类任务。 “决策树”这个名字来源于这样一个事实:算法不断地将数据集划分为越来越小的部分,直到数据被划分为单个实例,然后对实例进行分类。如果您要可视化算法的结果,类别的划分方式将类似于一棵树和许多叶子。
这是决策树的快速定义,但让我们深入了解决策树的工作原理。 更好地了解决策树的运作方式及其用例,将帮助您了解何时在机器学习项目中使用它们。
决策树的结构
决策树的结构类似于流程图,从一个起点或根节点开始,根据过滤条件的判断结果,逐级分支,直至达到树的末端,即叶子节点。每个内部节点代表一个特征的测试条件,而叶子节点则代表数据点的分类标签。
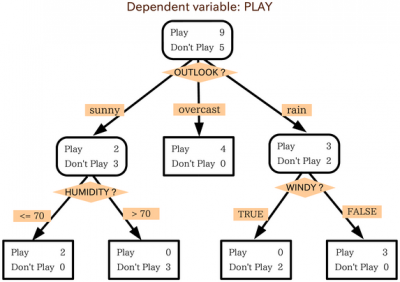
决策树是一种层次化的决策模型,它通过一系列的问题将数据分类。以下是决策树结构的关键组成部分和特性:
-
根节点(Root Node):
- 决策树的起点,代表整个数据集。
-
内部节点(Internal Nodes):
- 表示决策问题或属性测试。每个内部节点对应一个特征(或属性)的分割点。
-
分支(Branches):
- 从每个内部节点延伸出来,代表测试的不同结果。分支的数量取决于该节点特征的可能值。
-
叶子节点(Leaf Nodes):
- 树的末端,代表最终决策或分类结果。在分类问题中,叶子节点通常包含类别标签;在回归问题中,它们包含预测值。
-
路径(Path):
- 从根节点到任一叶子节点的连接序列,代表一系列决策规则。
-
分割(Split):
- 在内部节点处,根据特征值将数据集分割成子集的过程。
-
特征(Feature):
- 用于分割数据的特征或属性。
-
阈值(Threshold):
- 用于确定数据点是否沿着特定分支的值。
-
纯度(Purity):
- 衡量节点中数据点是否属于同一类别的指标。高纯度意味着节点中的数据点属于同一类别。
-
深度(Depth):
- 从根节点到树中任意节点的最长路径长度。
-
宽度(Width):
- 树中叶子节点的最大数量。
-
树高(Tree Height):
- 从根节点到最远叶子节点的边数。
-
基尼指数(Gini Index):
- 用于分类树的内部节点评估,衡量节点不纯度的指标。
-
熵(Entropy):
- 另一种衡量节点不纯度的指标,常用于构建分类树。
-
信息增益(Information Gain):
- 通过分割获得的信息量,用于选择最佳分割点。
-
决策规则(Decision Rules):
- 从根到叶的路径上的一系列决策,用于对数据点进行分类。
决策树的结构使得模型不仅能够进行预测,还能够解释预测背后的逻辑。这种可解释性使得决策树在需要模型透明度的应用中非常有用。然而,决策树也容易过拟合,特别是当树变得非常深和复杂时。因此,剪枝技术通常用于简化决策树,提高其泛化能力。
决策树算法
决策树的构建过程采用递归二元分割算法,该算法通过评估不同特征对数据集进行分割的效果,选择最佳分割点。分割的目的是使得每个子集尽可能地“纯”,即包含的数据点属于同一类别或具有相似的响应值。
分割成本的确定
决策树是一种常用用于分类和回归任务。在回归问题中,决策树的目标是预测一个连续的输出值。如果你使用决策树进行回归预测,并希望计算预测误差,你可以使用均方误差(Mean Squared Error, MSE)作为评估指标。MSE 衡量的是模型预测值与实际值之间差异的平方的平均值。
对于决策树来说,计算 MSE 的过程如下:
-
使用决策树模型进行预测:给定一个训练好的决策树模型,对于每个数据点,使用模型进行预测,得到预测值
prediction_i。 -
计算误差:对于每个数据点,计算其实际值
y_i与预测值prediction_i之间的差异,然后计算这个差异的平方。 -
求和:将所有数据点的误差平方求和。
-
平均:将求和结果除以数据点的总数
n,得到 MSE。
数学公式表示为:
M S E = 1 n ∑ i = 1 n ( y i − prediction i ) 2 {MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \text{prediction}_i)^2 MSE=n1i=1∑n(yi−predictioni)2
其中:
- n n n 是数据集中的样本数量。
- y i y_i yi
是第i` 个样本的实际值。 - p r e d i c t i o n i {prediction}_i predictioni 是模型对第
i个样本的预测值。
在 Python 中,如果使用 scikit-learn 库,可以很容易地计算决策树模型的 MSE。以下是一个简单的例子:
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error
import numpy as np# 假设 X 是特征数据,y 是目标变量
X = ... # 特征数据
y = ... # 目标变量# 创建决策树回归模型
tree_reg = DecisionTreeRegressor()# 训练模型
tree_reg.fit(X, y)# 进行预测
y_pred = tree_reg.predict(X)# 计算 MSE
mse = mean_squared_error(y, y_pred)
print(f"Mean Squared Error: {mse}")
MSE 仅适用于回归问题。如果你在处理分类问题,可能需要考虑其他指标,如准确率、召回率、F1 分数等。此外,MSE 对异常值敏感,因此在某些情况下,你可能还想使用其他指标,如平均绝对误差(Mean Absolute Error, MAE)来评估模型性能。
决策树的剪枝
决策树的剪枝是防止模型过拟合的重要技术。过拟合的决策树可能会在训练数据上表现良好,但在未见过的数据上泛化能力差。剪枝通过移除树中的一些分支来简化模型,从而提高其在新数据上的预测性能。以下是几种常见的决策树剪枝方法:
-
预剪枝(Pre-pruning):
- 在构建决策树的过程中,预剪枝会在树生长的每个阶段评估是否应该停止分裂。如果某个节点的分裂不能显著提高模型的性能,那么这个节点将被标记为叶子节点,不再进一步分裂。
-
后剪枝(Post-pruning):
- 后剪枝是在决策树完全生长完成后进行的。它从树的叶子节点开始,评估移除节点对模型性能的影响。如果移除某个节点后的模型性能没有显著下降,那么这个节点将被删除。
-
错误率降低剪枝(Reduced-Error Pruning):
- 这种方法是在后剪枝的基础上,通过比较剪枝前后的错误率来决定是否剪枝。如果剪枝后的模型在交叉验证集上的错误率没有增加,或者增加的幅度在可接受范围内,那么剪枝是成功的。
-
代价复杂性剪枝(Cost-Complexity Pruning):
- 代价复杂性剪枝是一种后剪枝技术,它通过引入一个参数来平衡模型的复杂度和预测误差。这种方法允许模型在剪枝过程中保持一定程度的复杂性,同时减少过拟合的风险。
-
最小描述长度剪枝(Minimum Description Length Pruning):
- 这种方法基于信息论原理,试图找到能够最小化描述模型和数据所需的信息量(即描述长度)的树。它考虑了模型的复杂性和预测误差,以找到最佳的剪枝点。
-
基于规则的剪枝:
- 在某些情况下,可以使用领域知识来定义规则,以指导剪枝过程。例如,如果某个特征在数据集中的分布非常不均匀,可以考虑剪枝掉依赖于该特征的分支。
使用决策树的注意事项
决策树在需要快速分类且计算时间受限的场景下非常有用。它们能够清晰地展示数据集中哪些特征最具预测力,并且与许多其他机器学习算法相比,决策树的规则更易于解释。此外,决策树能够处理分类变量和连续变量,减少了预处理的需求。
然而,决策树在预测连续属性值时可能表现不佳,且在类别众多而训练样本较少的情况下,分类准确性可能降低。
通过深入理解决策树的工作原理和特性,我们可以更好地判断在机器学习项目中何时使用它们,以及如何优化它们的性能。
相关文章:

深度神经网络——决策树的实现与剪枝
概述 决策树 是一种有用的机器学习算法,用于回归和分类任务。 “决策树”这个名字来源于这样一个事实:算法不断地将数据集划分为越来越小的部分,直到数据被划分为单个实例,然后对实例进行分类。如果您要可视化算法的结果…...

IOPaint前后端框架
IOPaint 前后端框架 IOPaint 是一个图像修复工具,使用了先进的AI模型进行图像编辑。以下是其前后端所使用的框架: 前端框架 IOPaint 的前端使用了 Node.js 和 npm 进行依赖管理和构建。具体步骤如下: 克隆仓库并进入 web_app 目录&#x…...
【Linux】进程间通信_2
文章目录 七、进程间通信1. 进程间通信分类管道 未完待续 七、进程间通信 1. 进程间通信分类 管道 管道的四种情况: ①管道内部没有数据,并且具有写端的进程没有关闭写端,读端就要阻塞等待,知道管道pipe内部有数据。 ②管道内部…...

Linux基础 - 常用命令
目录 零. 简介 一 . 常见 Ubuntu 命令 二. apt-get 下载 三. 网络命令 四. 常用命令的总结 零. 简介 在 Ubuntu 中,命令是用于与操作系统进行交互和执行各种操作的指令。通过在终端中输入命令,可以完成文件管理、系统配置、软件安装、进程管理等各种…...

轻松两步,借助向量数据库 VectorDB 与千帆 Appbuilder 构建个性化本地问答知识库
在我们日常的工作和生活中,经常会遇到需要快速获取和管理大量信息的情况。无论是解答客户的问题,还是整理公司内部的资料,一个高效的知识库系统都能帮我们省下大量时间和精力。 为了帮助大家快速构建 RAG 应用,我们之前发布了一个…...
ONLYOFFICE 桌面编辑器 8.1
ONLYOFFICE 桌面编辑器 8.1 ONLYOFFICE 简介一、轻松编辑器 PDF 文件二、用幻灯片版式快速修改幻灯片三、无缝切换文档编辑、审阅和查看模式四、**改进从右至左语言的支持 & 新的本地化选项**五、隐藏“连接到云”板块六、在演示文稿中播放视频和音频文件七、版本 8.1&…...
idea中的git在clone文件提示 filename too long
一 解决版本 1.1 问题描述以及解决办法 当在Windows系统下使用Git时出现“filename too long”错误: git config --system core.longpaths true...

C++ 数组介绍
1. 数组是什么? 在C中,数组是一种基本的数据结构,它允许我们存储固定大小的相同类型元素的集合。每个元素在数组中都有一个唯一的索引,从0开始。 2. 数组的声明与初始化 2.1 声明数组 声明数组时,需要指定数组的类…...

思维导图MindManager2024最新版,让你的思维飞起来!
亲爱的朋友们,今天我要跟大家分享一款我近期深度使用并彻底被种草的神器——MindManager2024最新版本的思维导图软件。作为一位对效率和创意有着极高追求的内容创作者,我几乎尝试过市面上所有的思维导图工具,而MindManager2024无疑是其中的佼…...
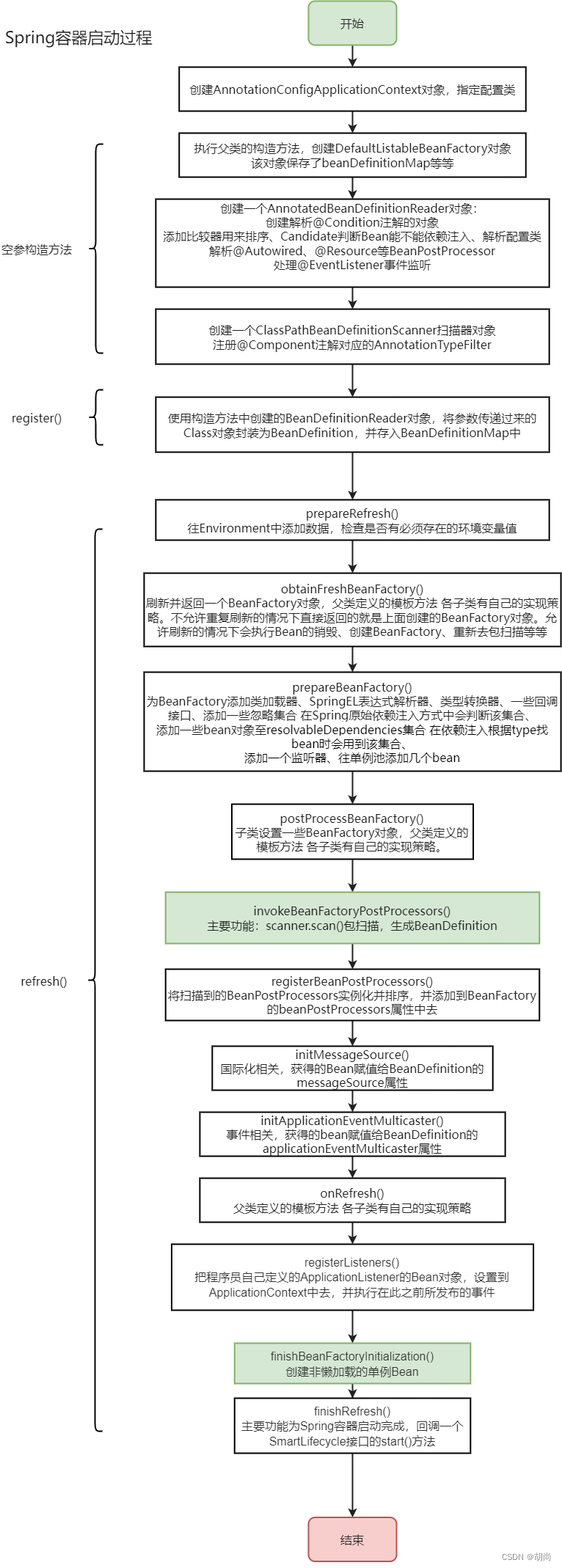
Spring容器启动流程——refresh()单个方法分析
文章目录 Spring启动过程this()方法refresh()prepareRefresh()obtainFreshBeanFactory()prepareBeanFactory()postProcessBeanFactory()invokeBeanFactoryPostProcessorsregisterBeanPostProcessorsinitMessageSource()initApplicationEventMulticaster()onRefresh()registerLi…...

Redis--注册中心集群 Cluster 集群
准备工作: 首先pull用到的镜像 docker pull redis:6.0.8 端口准备 node01 192.168.248.189.6381-6382 node02 192.168.248.190 6383-6384 node03 192.168.248.191 6385-6386 创建路径: mkdir -p /soft/docker/redis-cluster cd /soft/docker/re…...

秋招突击——6/20——复习{(单调队列优化)——最大子序列和,背包问题——宠物小精灵收服问题}——新作{两两交换链表中的节点}
文章目录 引言复习单调队列优化——最大子序列和思路分析实现代码参考实现 背包问题——宠物小精灵的收服问题个人实现参考实现 新作两两交换链表中的节点个人实现参考实现 删除有序数组中的重复项个人实现知识补全迭代器的访问和控制vector删除特定的元素erasevector底层删除元…...
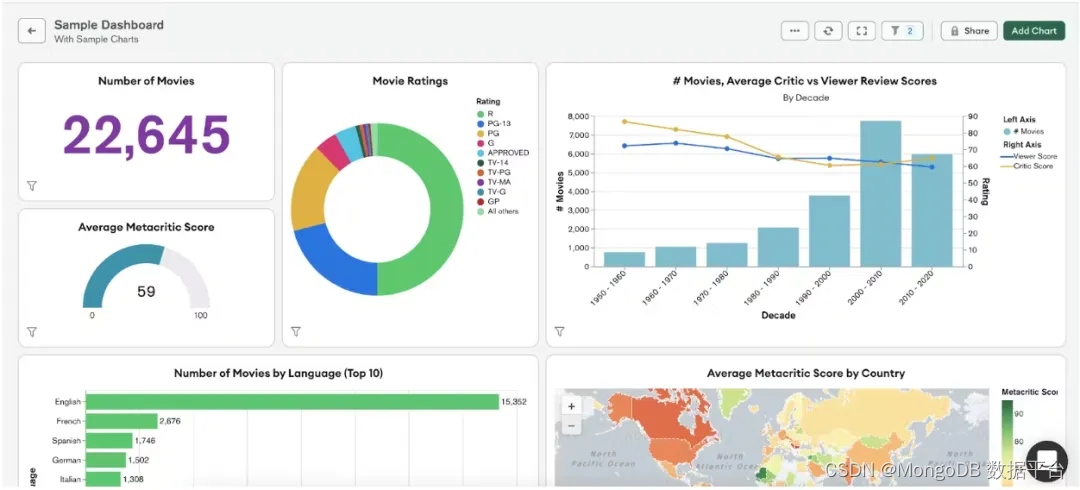
使用 MongoDB 剖析开放银行:技术挑战和解决方案
开放银行(或开放金融)在银行业掀起了一股颠覆性浪潮,它迫使金融机构(银行、保险公司、金融科技公司、企业甚至政府机构)迎接一个透明、协作和创新的新时代。这种模式转变要求银行与第三方提供商(TPP&#x…...
鸿蒙 HarmonyOS NEXT星河版APP应用开发-阶段二
一、鸿蒙应用界面开发 弹性布局-Flex 语法 /* 弹性容器组件 Flex() 位置: Flex默认主轴水平往右,交叉轴垂直向下(类似Row) 语法: Flex(参数对象){子组件1,子组件2,子组件3 } 属性方法: direction…...
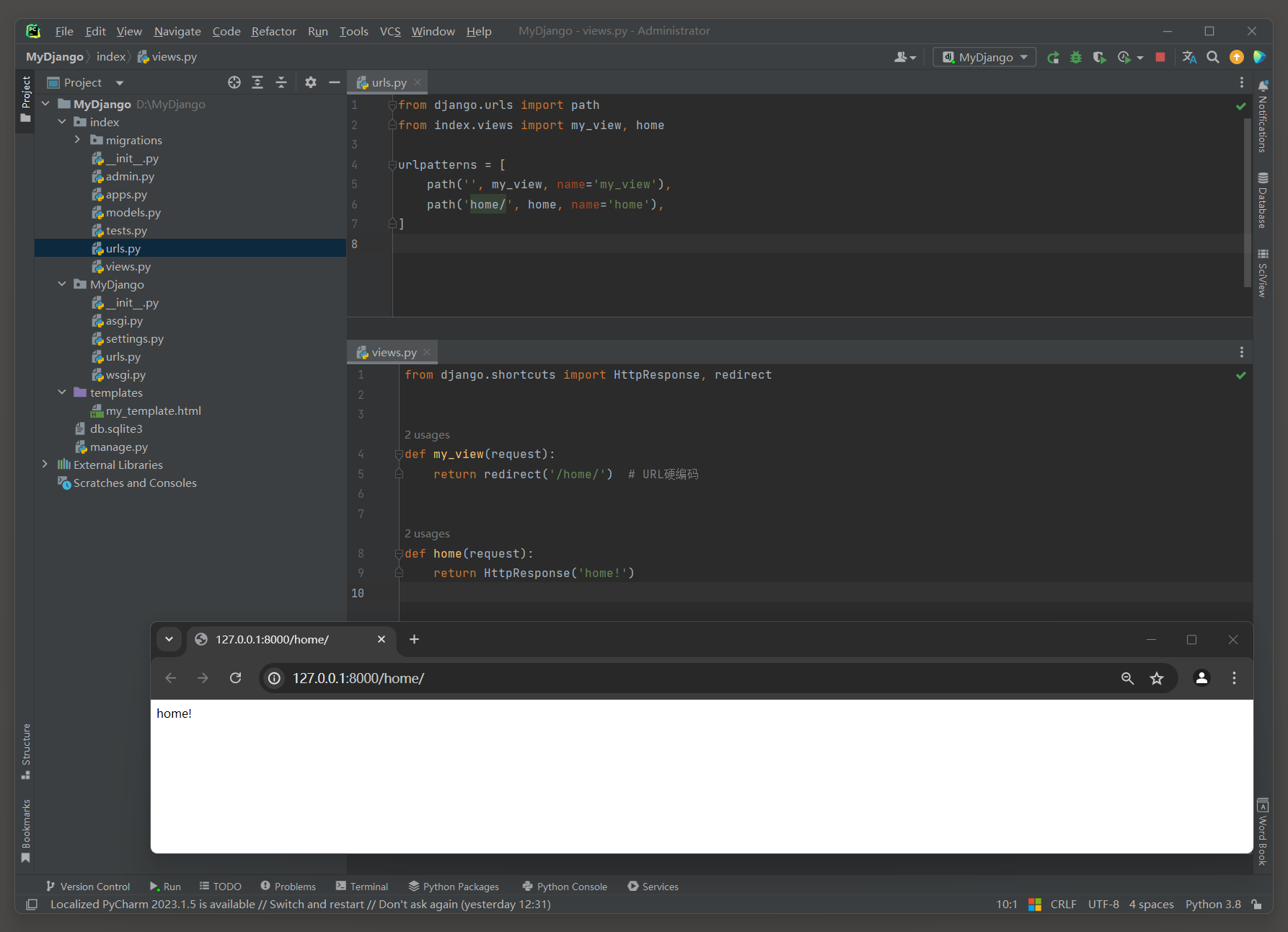
26.4 Django 视图层
1. 视图函数 视图函数是Django框架中用于处理Web请求并返回Web响应的重要组件. 以下是对Django视图函数的详细解释: * 1. 视图函数与URL的映射.为了让Django能够知道哪个URL对应哪个视图函数, 需要在应用的urls.py文件中定义URL模式.使用path或re_path函数来定义URL模式, 并将…...

Hbase介绍
Hbase介绍 HBase 是一个开源的、分布式的、面向列的 NoSQL 数据库系统,它建立在 Apache Hadoop 之上,提供了高可靠性、高性能、可伸缩性和高可用性的存储解决方案。让我来简单介绍一下 HBase 的架构。 1. 架构概述: HBase 的架构设计基于 Go…...
rollup学习笔记
一直使用的webpack,最近突然想了解下rollup,就花点时间学习下. 一,什么是rollup? rollup 是一个 JavaScript 模块打包器,可以将小块代码编译成大块复杂的代码,比如我们的es6模块化代码,它就可以进行tree shaking,将无用代码进行清除,打包出精简可运行的代码包. 业…...
多商户零售外卖超市外卖商品系统源码
构建你的数字化零售王国 一、引言:数字化零售的崛起 在数字化浪潮的推动下,零售业务正经历着前所未有的变革。多商户零售外卖超市商品系统源码应运而生,为商户们提供了一个全新的数字化零售解决方案。通过该系统源码,商户们可以…...

HTML 教程
HTML 教程 HTML(HyperText Markup Language)是一种用于创建网页的标准标记语言。它描述了一个网站的结构骨架,使得浏览器能够展示具有特定格式的文本、链接、图片和其他内容。本教程将带你深入了解HTML的基础知识,包括其语法、常用标签以及如何构建一个基本的网页结构。 …...
【仿真建模-解析几何】求有向线段上距指定点最近的坐标
Author:赵志乾 Date:2024-06-25 Declaration:All Right Reserved!!! 问题描述: 有向线段起点A为(x1,y1),终点B为(x2,y2&a…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
