口感探险之旅:勇闯红酒世界,揭秘复杂风味的无尽奥秘
在葡萄酒的浩瀚海洋中,红酒如同一座深邃而迷人的岛屿,等待着勇敢的探险家们去发掘其背后隐藏的奥秘。每一次品尝红酒,都是一次口感的大冒险,让我们在味蕾的舞动中感受那千变万化的风味。今天,就让我们一起踏上这场探索红酒复杂风味的旅程,与雷盛红酒一同领略其中的魅力。

一、红酒风味之旅的序幕
当我们轻轻旋转酒瓶,倒出那深红色的液体时,红酒的冒险之旅便悄然拉开序幕。首先,我们被那浓郁的果香所吸引,仿佛置身于一个硕果累累的果园之中。接着,随着红酒与空气的接触,它的香气逐渐变得更加复杂,橡木桶、香草、烟草等多种香气交织在一起,让人陶醉其中。
二、红酒风味的层次与变化
红酒的风味并非一成不变,而是随着时间的推移和氧气的接触而逐渐演变。在初尝时,我们可能只能感受到红酒的果香和酸度;但随着时间的推移,单宁、酒精和甜度等元素逐渐显现出来,使得红酒的风味变得更加丰富和复杂。这种层次感和变化性正是红酒魅力所在。

三、雷盛红酒:风味之旅的领着者
在众多的红酒品牌中,雷盛红酒通过其不同的风味和品质成为了这场风味之旅的受宠者之一。雷盛红酒选用上好的葡萄品种,经过精心的酿造和陈年,呈现出不同而复杂的风味。每一款雷盛红酒都如同一位优雅的舞者,在味蕾上翩翩起舞,让人陶醉其中。
在品尝雷盛红酒时,我们首先感受到的是那浓郁的果香和酸度,仿佛置身于一个阳光明媚的葡萄园中。接着,随着红酒在口腔中的扩散和氧气的接触,单宁的涩感逐渐显现出来,与果香和酸度相互交织在一起,形成了一种不同的口感。同时,酒精的温暖和甜度的回甘也为红酒增添了一抹柔和的韵味。这种复杂而多变的风味让人回味无穷,仿佛置身于一场美妙的味觉盛宴之中。
四、探索红酒风味的乐趣
探索红酒的复杂风味不仅仅是一种味蕾的享受更是一种生活的乐趣。在品尝红酒的过程中我们需要仔细观察红酒的颜色、闻其香气、品味其口感并感受其层次和变化。这种细致入微的品酒方式让我们更加深入地了解红酒的魅力和特点同时也让我们在品酒的过程中感受到一种不同的宁静和满足。
此外探索红酒的风味也是一种文化的传承和体验。在红酒的世界里我们不仅可以品尝到各种美味的红酒还可以了解到不同产区的风土人情、酿酒技艺和历史文化。这种文化的传承和体验让我们更加深入地了解红酒的魅力和价值也让我们在品酒的过程中感受到一种文化的熏陶和洗礼。

五、结语:品味红酒的复杂风味
在口感的大冒险中我们与红酒相遇并一同探索其复杂而多变的风味。雷盛红酒作为这场风味之旅的领着者以其不同的风味和品质让我们陶醉文化之中。让我们继续品味红酒的复杂风味感受其中的乐趣和魅力共同领略红酒世界的无限精彩!
相关文章:

口感探险之旅:勇闯红酒世界,揭秘复杂风味的无尽奥秘
在葡萄酒的浩瀚海洋中,红酒如同一座深邃而迷人的岛屿,等待着勇敢的探险家们去发掘其背后隐藏的奥秘。每一次品尝红酒,都是一次口感的大冒险,让我们在味蕾的舞动中感受那千变万化的风味。今天,就让我们一起踏上这场探索…...

吉时利 Keithley2440 数字源表
Keithley2440吉时利SMU数字源表 Keithley2440 - 40V、5A、50W源表 吉时利数字源表系列专用于要求紧密结合源和测量 的测试应用。全部数字源表型号都提供精密电压源和电 流源以及测量功能。每款数字源表既是高度稳定的直流 电源也是真仪器级的6位半万用表。此电源的特性包括 低…...

PPT的精细化优化与提升策略
👏👏👏欢迎来到我的博客 ! 亲爱的朋友们,欢迎您们莅临我的博客!这是一个分享知识、交流想法、记录生活的温馨角落。在这里,您可以找到我对世界独特视角的诠释,也可以与我一起探讨各种话题&#…...

awtk踩坑记录三:移植awtk-mvvm到Awtk Designer项目
从github下载并编译awtk, awtk-mmvm awtk: https://github.com/zlgopen/awtk/tree/master awtk-mvvm: https://github.com/zlgopen/awtk-mvvm 用awtk-designer新建项目并打开项目目录 首先修改project.json,使其awtk和awtk-mvvm指向上个步骤下载的路径,…...

07 - matlab m_map地学绘图工具基础函数 - 绘制等高线
07 - matlab m_map地学绘图工具基础函数 - 绘制等高线 0. 引言1. 关于绘制m_contour2. 关于绘制m_contourf3. 关于绘制m_elev4. 结语 0. 引言 本篇介绍下m_map中添加绘制等高线的一系列函数及其用法,主要函数包括m_elev、m_contour、m_contourf还有一些函数也和绘制…...
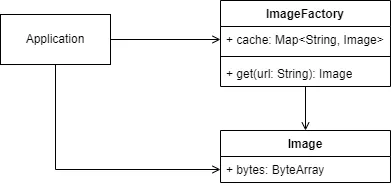
Kotlin设计模式:享元模式(Flyweight Pattern)
Kotlin设计模式:享元模式(Flyweight Pattern) 在移动应用开发中,内存和CPU资源是非常宝贵的。享元模式(Flyweight Pattern)是一种设计模式,旨在通过对象重用来优化内存使用和性能。本文将深入探…...

java压缩pdf
<!-- PDF操作,itext7全家桶 --><dependency><groupId>com.itextpdf</groupId><artifactId>itext7-core</artifactId><version>7.1.15</version><type>pom</type></dependency>package org.example; import…...

[AIGC] ClickHouse:一款高性能列式数据库管理系统
轮流探索数据库的世界,我们不得不提到一个重要的角色——ClickHouse。ClickHouse是一个开源的列式数据库管理系统(DBMS),以其卓越的性能,高效的查询能力和易扩展性而被业界广泛关注,尤其在大数据分析方面。 文章目录 1. 什么是 Cl…...

深度学习21-30
1.池化层作用(筛选、过滤、压缩) h和w变为原来的1/2,64是特征图个数保持不变。 每个位置把最大的数字取出来 用滑动窗口把最大的数值拿出来,把44变成22 2.卷积神经网络 (1)conv:卷积进行特征…...

google浏览器无法访问大端口的处理方式
属性的目标中添加后缀内容或者修改后台端口为常用端口,比如8080等。 “C:\Program Files\Google\Chrome\Application\chrome.exe” --explicitly-allowed-ports8888...

微信小程序余额退费
需求:用户充值使用后的剩余金额,需要退回到用户原路。 参考文档:微信支付-开发者文档 pom.xml配置: <!--微信支付SDK--> <dependency><groupId>com.github.wechatpay-apiv3</groupId><artifactId&g…...

宁波银行票据案例解读,要注入科技赋能票据新形式
随着科技的飞速发展,金融行业正迎来一场前所未有的变革。作为一家以科技创新为驱动的现代化银行,宁波银行在这场变革中积极探索,宁波银行票据案例之后持续通过引入先进技术,为客户提供更加高效、智能的金融服务。 宁波银行推出的…...

博客已迁移
迁移至 烧烤er (makkapakka996.github.io)...

大模型应用研发基础环境配置(Miniconda、Python、Jupyter Lab、Ollama等)
老牛同学之前使用的MacBook Pro电脑配置有点旧(2015 年生产),跑大模型感觉有点吃力,操作起来有点卡顿,因此不得已捡起了尘封了快两年的MateBook Pro电脑(老牛同学其实不太喜欢用 Windows 电脑做研发工作&am…...

24年嘉兴市索贝进出口有限公司--信息安全实施项目
截至24年6月24日,oms生产环境订单数12万5673条。 索贝是一家致力于成为竹木小家具头部企业的公司,截至24年6月24日,在册员工数130人,产值10个亿。 由于信息安全人才和能力的缺失,导致部署在阿里云生产环境的系统处于…...
亚马逊云科技官方活动:一个月拿下助理架构师SAA+云从业者考试认证(送半价折扣券)
为了帮助大家考取AWS SAA和AWS云从业者认证,小李哥争取到了大量考试半价50%折扣券,使用折扣券考试最多可省75刀(545元人民币)。 领取折扣券需要加入云师兄必过班群,在群中免费领取。目前必过班群招募到了超过200名小伙伴,名额有限…...
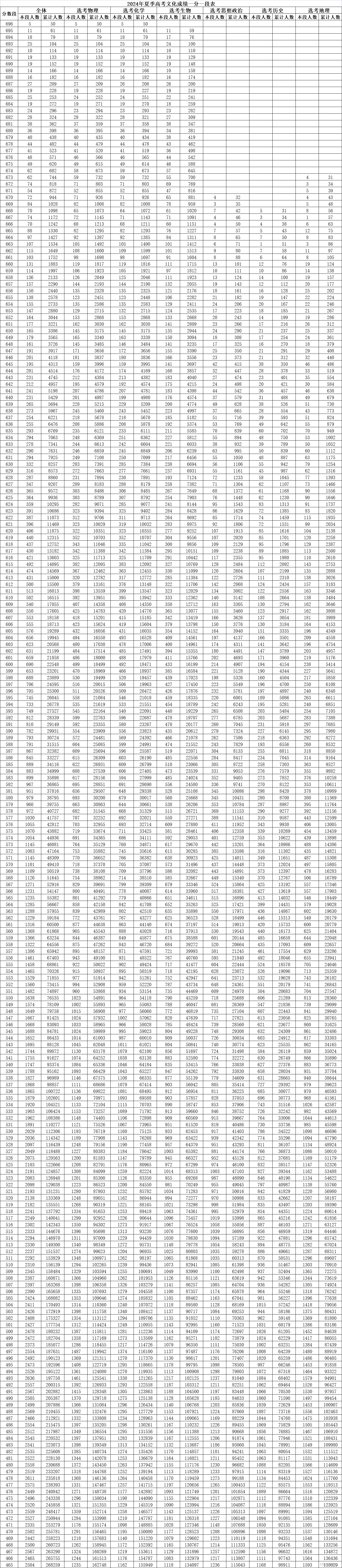
【山东】2024年夏季高考文化成绩一分一段表
文末有图片版,可直接保存下载!! 2024年夏季高考文化成绩一分一段表分数段全体-选考物理-选考化学-选考生物-选考思想政治-选考历史-选考地理分数段本段人数累计人数本段人数累计人数本段人数累计人数本段人数累计人数本段人数累计人数本段人…...

栈与队列 Leetcode 347 前k个高频元素
栈与队列 Leetcode 347 前k个高频元素 Leetcode 347 灵活运用C库函数,使用匿名函数排序,sort可以替换为快排实现(面试感觉可能会手撕,机考直接使用sort) class Solution { public:vector<int> topKFrequent(v…...

windchill 相关配置
-Dhttp.proxyHostproxy.acme.com -Dhttp.proxyPort8080 -Dwt.rmi.clientSocketFactorywt.boot.WTRMIMasterSocketFactory -Dwt.rmi.javarmicgiservlet/JavaRMIServlet...

XGBoost算法深度解析:原理、实现与应用
摘要 XGBoost(eXtreme Gradient Boosting)是一种高效的机器学习算法,以其出色的预测性能和计算效率在众多数据科学竞赛和实际应用中取得了巨大成功。本文将深入探讨XGBoost算法的基本原理、实现机制、优化技巧以及在不同领域的应用案例。 1…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...
