扩展欧几里得算法及其应用
前言
由于数论的板子真的很抽象,也很难背,所以特此记录扩展欧几里得算法的板子和它的用途
本篇文章只涉及应用,不涉及证明,如需理解证明还请各位移步其他优秀的讲解!
扩展欧几里得算法
先粘一下板子的代码
typedef long long LL ; LL exgcd(LL a, LL b, LL &x, LL &y) {if (!b) {x = 1, y = 0 ; return a ; }LL d = exgcd(b, a % b, y, x) ; y -= a / b * x ; return d ; }
变量解释
对于方程:ax + by = d
其中 a 和 b 都是常数 (已知量),d 是 a 和 b 的最大公约数
x 和 y 是我们希望求得的一组满足方程的解
应用例题

题目链接🔗:222. 青蛙的约会 - AcWing题库
题目分析

AC代码
#include <iostream>
#include <algorithm>
#include <cstring>using namespace std ;typedef long long LL ; LL exgcd(LL a, LL b, LL &x, LL &y)
{if (!b) {x = 1, y = 0 ; return a ; }LL d = exgcd(b, a % b, y, x) ; y -= a / b * x ; return d ;
}int main()
{ios::sync_with_stdio(false) ; LL a, b, m, n, L ; cin >> a >> b >> m >> n >> L ;LL x, y ; LL d = exgcd(m - n, L, x, y) ; if ((b - a) % d) cout << "Impossible" << endl ;else {x *= (b - a) / d ; LL t = abs(L / d) ; cout << (x % t + t) % t << endl ; // 求最小正整数解}return 0 ;
}难点解释
为什么要计算 t ?
解释:
题解来源🔗: AcWing 222. 青蛙的约会 - AcWing
再来一道题目巩固一下
同余方程模版题 🔗203. 同余方程 - AcWing题库
题目描述

题目分析
a * x % b = 1 等价于找到两个数 x 和 y 使得 a * x + b * y = 1
这恰好是我们扩展欧几里得算法的基本解决对象,直接套板子就行了,由于题目保证输入一定有解,所以我们可以认为 a 和 b 是互质的,因此可以使用扩展欧几里得算法。
最后记得对b取模保证答案为最小正数。
AC代码
#include <iostream>
#include <algorithm>
#include <cstring>using namespace std ;typedef long long LL ; int exgcd(int a, int b, int &x, int &y)
{if (!b) {x = 1, y = 0 ; return a ; }int d = exgcd(b, a % b, y, x) ; y -= a / b * x ; return d ;
}int main()
{ios::sync_with_stdio(false) ; int a, b ; cin >> a >> b ; int x, y ; exgcd(a, b, x, y) ; cout << (x % b + (LL)b) % b << endl ; return 0 ;
}END
相关文章:

扩展欧几里得算法及其应用
前言 由于数论的板子真的很抽象,也很难背,所以特此记录扩展欧几里得算法的板子和它的用途 本篇文章只涉及应用,不涉及证明,如需理解证明还请各位移步其他优秀的讲解! 扩展欧几里得算法 先粘一下板子的代码 typedef lo…...

JAVA练习75-全排列
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 前言 提示:这里可以添加本文要记录的大概内容: 3月11日练习内容 提示:以下是本篇文章正文内容,下面案例可供参考 一、题目-…...
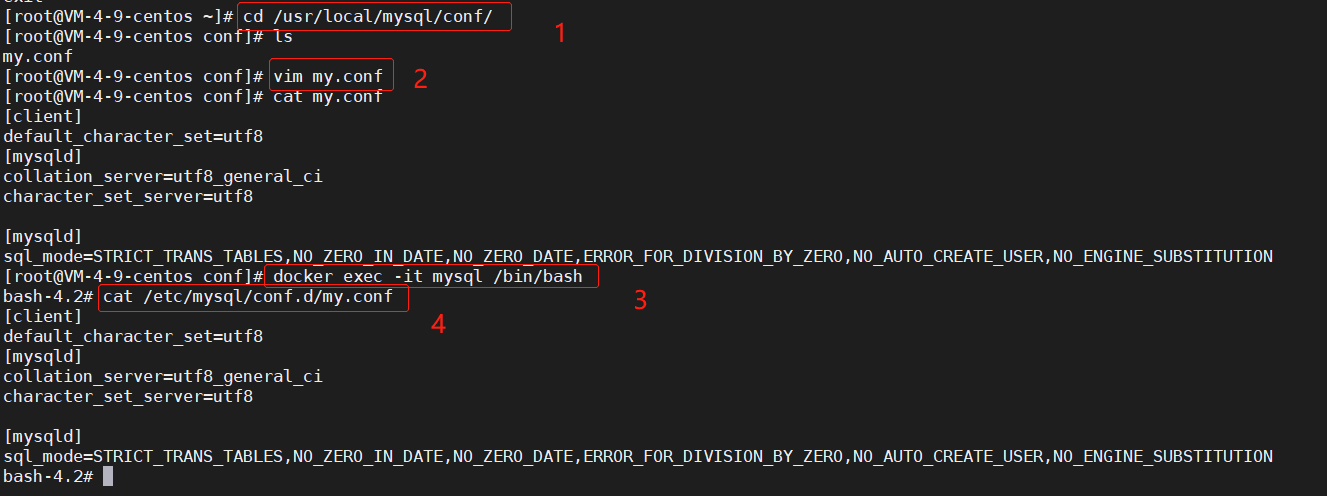
Linux下Docker安装mysql-超详细步骤
安装Docker Engine官方参考文档:https://docs.docker.com/engine/install/centos/若之前有安装docker,需要先卸载之前的dockersudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \d…...

弹性存储-对象存储OSS部分
对象存储介绍 对象存储(object storage service,简称oss),具备与平台无关的rest api接口,可提供99.9999999999%(12个9)的数据持久性和99.995%的数据可用性。 OSS优势 功能介绍 存储空间bucke…...

强推!30个遥感数据下载网站整理分享
1、中国遥感数据共享网(http://rs.ceode.ac.cn/)国内存档周期最长的数据网站,对Landsat数据免费共享,也可订购国外商业卫星数据。注册账号,通过审核就可直接下载。2、中国资源卫星应用中心(https://data.cr…...
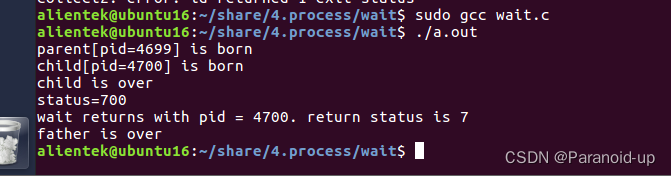
进程系统调用
进程系统调用 文章目录进程系统调用fork()进程创建:fock()fork函数fork用法僵尸进程孤儿进程vfork函数vfork与fork区别exec函数族exec函数族-何时使用?exec函数族语法exec函数族使用区别exit和_exit_exit和exit的区别wait和waitpidfork() 进程创建&…...

dubbo进阶——服务导出
服务导出 在这里记录一下对" Dubbo 导出服务的过程"的研究。 触发时机 public class ServiceBean<T> extends ServiceConfig<T> implements InitializingBean, DisposableBean, ApplicationContextAware, ApplicationListener<ContextRefreshedEv…...

【竞品分析】如何撰写竞品分析?竞品分析的基本结构?以及优秀的竞品分析案例
文章目录一、撰写竞品分析的意义二、撰写的节点三、竞品分析内容的基本结构四、总结本文对视频 如何撰写竞品分析(demo)进行了总结。一、撰写竞品分析的意义 竞品分析是指对现有的或潜在的竞争产品的优势和劣势进行评价。现在被广泛应用于互联网产品的…...

海思ubootsd卡协议
在start_armboot()函数中调用mmc_initialize(0)初始化mmc;最终调用到int hi_mci_initialize(unsigned int dev_num)函数;内容如下:static int hi_mci_initialize(unsigned int dev_num) {struct mmc *mmc NULL;static struct himci_host *host;unsigned int regval;unsigned l…...

nuxt3使用总结
目录 背景 安装 项目配置 路由 Tailwindcss引入 全局样式配置 css预处理器 安装 Tailwindcss 项目的配置 部署上线 seo优化 背景 新入职了一家公司,刚进入公司第一个需求就是先做一个公司的官网,需要使用vue写,作为祖师爷的粉丝…...

指向函数的指针详解,以及如何使用指向函数的指针变量做函数参数
指向函数的指针作为函数参数,是 C 语言实际应用中的一个比较深入的部分。 目录 一、什么是函数的指针 二、用函数指着变量调用函数 2.1举例说明 三、怎样定义和使用指向函数的指针变量 3.1定义指向函数的指针变量 3.2指向函数的指针变量详解 3.3通过指针变量…...
Spring——spring整合JUnit
JUnit定义: Junit测试是程序员测试,即所谓 白盒测试 ,因为程序员知道被测试的软件如何(How)完成功能和完成什么样(What)的功能。 Junit是一套框架,继承TestCase类,就可以用Junit进行…...

保障信息安全:使用PyZbar库识别二维码图片可以快速获取二维码中的信息,保障信息安全。
目录 简介: 源代码: 源代码说明: 效果如下所示: 简介: 不用摄像头识别二维码可以应用在以下场景: 批量处理二维码图片:可以在服务器上使用PyZbar等库来批量处理二维码图片,例如读…...

从LeNet到ResNet:深入探索卷积神经网络
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
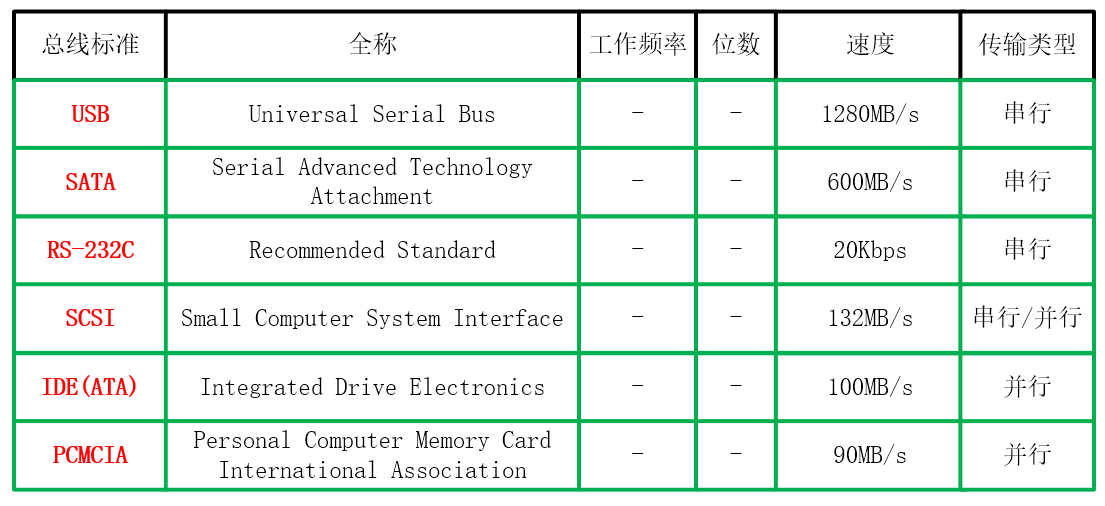
计算机组成原理_总线标准
计算机组成原理总目录总线标准 总线标准是系统与各模块、模块与模块之间的一个互连的标准,就像我们用汉语来相互交流一样。 1. 系统总线 ISA总线的扩展插槽,其颜色一般为黑色,比PCI接口插槽要长些,位于主板的最下端。 可插接显卡&…...

蓝桥杯C/C++VIP试题每日一练之芯片测试
💛作者主页:静Yu 🧡简介:CSDN全栈优质创作者、华为云享专家、阿里云社区博客专家,前端知识交流社区创建者 💛社区地址:前端知识交流社区 🧡博主的个人博客:静Yu的个人博客 🧡博主的个人笔记本:前端面试题 个人笔记本只记录前端领域的面试题目,项目总结,面试技…...

树莓派测试wifi与eth速率
测试网速方法: 1.安装插件: 首先在树莓派端安装iperf3 sudo apt install iperf3PC端也需要安装iperf3,单击下面网址即可 下载网址 压缩包解压到桌面,文件内容如下图所示: 2.开始测速服务: 树莓派端在…...

关系抽取方面的基础
关系抽取方面的基础一、基本概念1. 什么是关系抽取(Relation Extraction,RE)?2. 都有什么奇怪的关系?3. 任务评价指标二、 关系抽取方法2.1 按模型结构分——Pipeline 和 Joint方法Pipeline方法Joint方法2.2 按解码方式…...
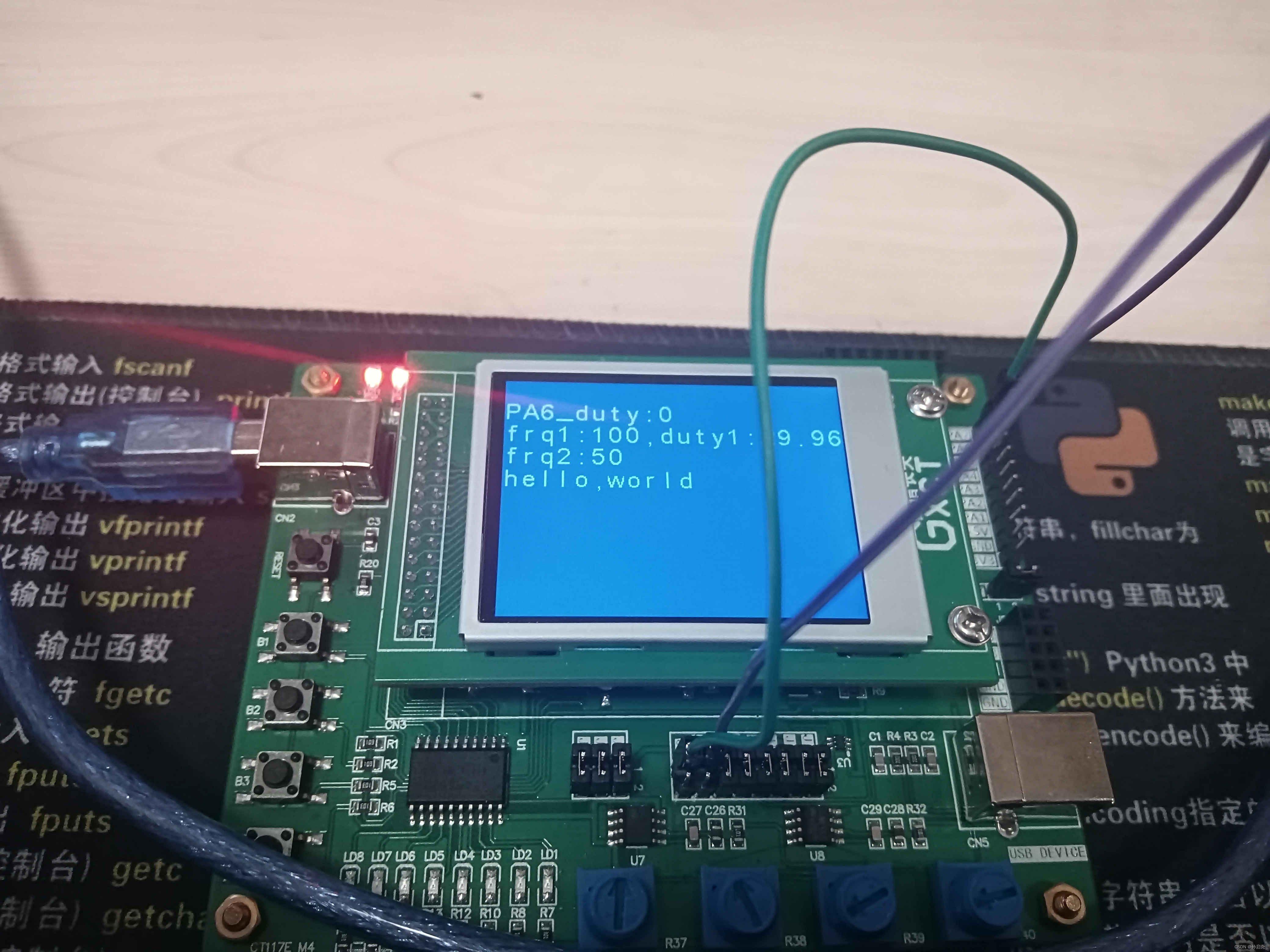
蓝桥杯嵌入式(G4系列):定时器捕获
前言: 定时器的三大功能还剩下最后一个捕获,而这在蓝桥杯嵌入式开发板上也有555定时器可以作为信号发生器供定时器来测量。 原理图部分: 开发板上集成了两个555定时器,一个通过跳线帽跟PA15相连,最终接到了旋钮R40上&…...
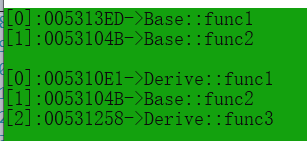
多态的定义、重写、原理
多态 文章目录多态多态的定义和条件协变(父类和子类的返回值类型不同)函数隐藏和虚函数重写的比较析构函数的重写关键字final和override抽象类多态的原理单继承和多继承的虚函数表单继承下的虚函数表多继承下的虚函数表多态的定义和条件 定义࿱…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

