OpenCV cv::Mat到 Eigen 的正确转换——cv2eigen
在进行计算机视觉项目时,我们经常需要处理相机位姿的变换。最近,我在项目中遇到了一个看似简单但实际上颇具挑战性的问题:从 OpenCV 的 cv::Mat 格式转换到 Eigen 库的格式。这个过程中遇到了一些问题,但最终找到了一个稳健的解决方案。
问题描述: 我们有两个表示相机位姿的 4x4 变换矩阵,格式为 cv::Mat。目标是计算这两个位姿之间的变换,并提取出平移向量。
初始尝试: 最初,我们尝试直接从 cv::Mat 中提取平移向量:
Eigen::Vector3d transLast(mLastFrameTcw.at<double>(0, 3),mLastFrameTcw.at<double>(1, 3),mLastFrameTcw.at<double>(2, 3)
);
Eigen::Vector3d transCurrent(mCurrentFrameTcw.at<double>(0, 3),mCurrentFrameTcw.at<double>(1, 3),mCurrentFrameTcw.at<double>(2, 3)
);
TRANS_PRED = transCurrent - transLast;遇到的问题: 针对简单的工程,代码运行完全没有问题,但是放到复杂工程里面,代码就会输出莫名其妙的结果!!!!!这种方法可能会导致错误,原因如下:
- 直接访问 cv::Mat 的元素可能不安全,特别是当矩阵的存储格式不确定时。
- 这种方法忽略了旋转部分的影响,可能导致计算结果不准确。
- 在某些情况下,可能会出现索引错误或类型不匹配的问题。
改进的解决方案: 经过多次尝试和改进,我们最终采用了以下方法:
// 直接相减 cv::Mat
cv::Mat diff = mCurrentFrameTcw - mLastFrameTcw;// 将 cv::Mat 转换为 Eigen 矩阵
Eigen::MatrixXd eigenDiff;
cv::cv2eigen(diff, eigenDiff);// 从 eigenDiff 的最后一列提取前三个元素赋值给 TRANS_PRED
TRANS_PRED = eigenDiff.block<3,1>(0, eigenDiff.cols()-1);这个解决方案的优点:
- 使用 cv::Mat 的矩阵减法,保持了原始数据的完整性。
- 利用 OpenCV 提供的 cv2eigen 函数,安全地将 cv::Mat 转换为 Eigen 矩阵。
- 使用 Eigen 的 block 操作,精确地提取所需的平移向量。
结论: 在处理计算机视觉中的坐标变换问题时,正确地在不同库(如 OpenCV 和 Eigen)之间转换数据格式是至关重要的。通过采用矩阵减法和适当的类型转换,我们可以准确地计算相机位姿之间的变换。这个经验教训提醒我们,在处理不同库之间的数据转换时,要特别注意数据类型的一致性和操作的正确性。在future类似的问题中,我们可以借鉴这种方法,确保在不同数学库之间进行安全和准确的数据转换。
下面给出完整的代码(注意:下面的两个版本都可以用,只是区分两个中哪个更鲁棒!!!)
#include <iostream>
#include <iomanip>
#include <opencv2/core.hpp>
#include <Eigen/Dense>
#include <opencv2/core/eigen.hpp>void CalculateTransPred_Method1(const cv::Mat& mLastFrameTcw, const cv::Mat& mCurrentFrameTcw, Eigen::Vector3d& TRANS_PRED) {std::cout << "Method 1: Direct extraction from cv::Mat" << std::endl;Eigen::Vector3d transLast(mLastFrameTcw.at<double>(0, 3),mLastFrameTcw.at<double>(1, 3),mLastFrameTcw.at<double>(2, 3));Eigen::Vector3d transCurrent(mCurrentFrameTcw.at<double>(0, 3),mCurrentFrameTcw.at<double>(1, 3),mCurrentFrameTcw.at<double>(2, 3));std::cout << "transLast: " << transLast.transpose() << std::endl;std::cout << "transCurrent: " << transCurrent.transpose() << std::endl;TRANS_PRED = transCurrent - transLast;std::cout << "TRANS_PRED: " << TRANS_PRED.transpose() << std::endl;
}void CalculateTransPred_Method2(const cv::Mat& mLastFrameTcw, const cv::Mat& mCurrentFrameTcw, Eigen::Vector3d& TRANS_PRED) {std::cout << "\nMethod 2: Using cv::Mat subtraction and Eigen conversion" << std::endl;cv::Mat diff = mCurrentFrameTcw - mLastFrameTcw;Eigen::MatrixXd eigenDiff;cv::cv2eigen(diff, eigenDiff);std::cout << "Difference (diff) in Eigen::MatrixXd format:" << std::endl;std::cout << eigenDiff << std::endl;TRANS_PRED = eigenDiff.block<3,1>(0, eigenDiff.cols()-1);std::cout << "TRANS_PRED: " << TRANS_PRED.transpose() << std::endl;
}int main() {cv::Mat mLastFrameTcw = (cv::Mat_<double>(4, 4) -0.1642483, 0.094168551, -0.98191381, 0.90703607,0.0095526827, 0.99553794, 0.093877248, -0.038507219,0.98637277, 0.0060392693, -0.164415, -3.4207926,0, 0, 0, 1);cv::Mat mCurrentFrameTcw = (cv::Mat_<double>(4, 4) -0.16892175, 0.093616515, -0.98117346, 0.92409742,0.009967736, 0.99559039, 0.093275994, -0.039425559,0.98557907, 0.0059762667, -0.16911002, -3.4853551,0, 0, 0, 1);Eigen::Vector3d TRANS_PRED;std::cout << std::fixed << std::setprecision(6);std::cout << "mLastFrame.mTcw:" << std::endl;std::cout << mLastFrameTcw << std::endl;std::cout << "\nmCurrentFrame.mTcw:" << std::endl;std::cout << mCurrentFrameTcw << std::endl;CalculateTransPred_Method1(mLastFrameTcw, mCurrentFrameTcw, TRANS_PRED);CalculateTransPred_Method2(mLastFrameTcw, mCurrentFrameTcw, TRANS_PRED);return 0;
}相关文章:

OpenCV cv::Mat到 Eigen 的正确转换——cv2eigen
在进行计算机视觉项目时,我们经常需要处理相机位姿的变换。最近,我在项目中遇到了一个看似简单但实际上颇具挑战性的问题:从 OpenCV 的 cv::Mat 格式转换到 Eigen 库的格式。这个过程中遇到了一些问题,但最终找到了一个稳健的解决…...
-常用的扩展-pg_pathman)
PostgreSQL的扩展(extensions)-常用的扩展-pg_pathman
PostgreSQL的扩展(extensions)-常用的扩展-pg_pathman pg_pathman 是一个用于 PostgreSQL 的分区管理扩展。它提供了一种高效的方式来管理和使用数据库分区,可以显著提升查询性能,特别是在处理大规模数据集时。 安装 pg_pathman…...
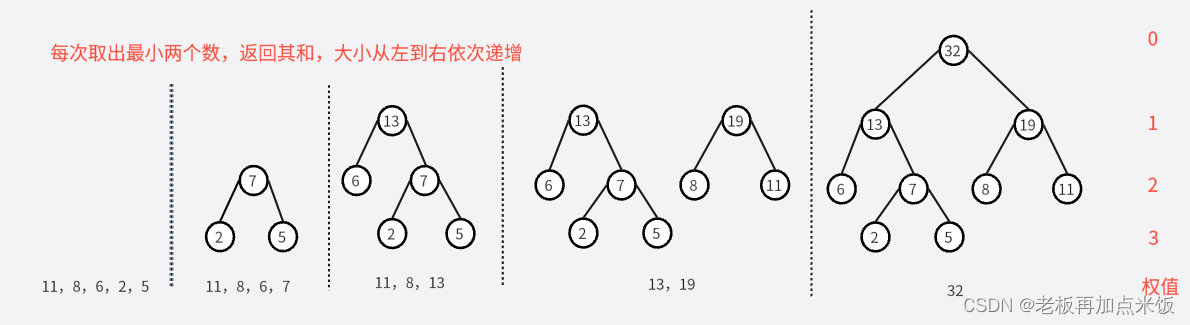
数据结构之树
基础知识: 树是一种非线性结构,其严格的数学定义是:如果一组数据中除了第一个节点(第一个节点称为根节点,没有直接前驱节点)之外,其余任意节点有且仅有一个直接前驱,有零个或多个直接…...

6毛钱SOT-23封装28V、400mA 开关升压转换器,LCD偏置电源和白光LED应用芯片TPS61040
SOT-23-5 封装 TPS61040 丝印PHOI 1 特性 • 1.8V 至 6V 输入电压范围 • 可调节输出电压范围高达 28V • 400mA (TPS61040) 和 250mA (TPS61041) 内部开关电流 • 高达 1MHz 的开关频率 • 28μA 典型空载静态电流 • 1A 典型关断电流 • 内部软启动 • 采用 SOT23-5、TSOT23…...

saga模型
Saga源于Hector Garcaa-Molrna和Kenneth Salem发表的论文Sagas。一个LLT事务(Long Lived Transaction)可以分成若干个小的事务执行单元,这些小执行单元就是saga事务。Saga方案更适合用于长事务场景。Saga模型将一个分布式事务拆分为多个本…...

深度神经网络:解锁智能的密钥
深度神经网络:解锁智能的密钥 在人工智能的浩瀚星空中,深度神经网络(Deep Neural Networks, DNNs)无疑是最耀眼的那颗星。它以其强大的学习能力、高度的适应性和广泛的应用场景,成为了我们解锁智能世界的一把密钥。本…...

国际现货黄金最新价格如何分析?结合较高的时间周期
国际现货黄金投资是一种24小时交易的品种,这意味着,在交易日我们打开电脑图表,分析完走势之后就有机会做交易了。但问题也出在这里,如果对国际现货黄金最新价格把握不住,分析和交易就无从谈起了,下面我们就…...

微服务和kafka
一、微服务简介 1.单体架构 分布式--微服务--云原生 传统架构(单机系统),一个项目一个工程:比如商品、订单、支付、库存、登录、注册等等,统一部署,一个进程 all in one的架构方式,把所有的…...

Jetpack架构组件_Navigaiton组件_1.Navigaiton切换Fragment
1.Navigation主要作用 方便管理Fragment (1)方便我们管理Fragment页面的切换 (2)可视化的页面导航图,便于理清页面间的关系。 (3)通过destination和action完成页面间的导航 (4&a…...

[计算机网络] 虚拟局域网
虚拟局域网 VLAN(Virtual Local Area Network,虚拟局域网)是将一个物理的局域网在逻辑上划分成多个广播域的技术。 通过在交换机上配置VLAN,可以实现在同一个VLAN 内的用户可以进行二层互访,而不同VLAN 间的用户被二…...

LabVIEW遇到无法控制国外设备时怎么办
当使用LabVIEW遇到无法控制国外产品的问题时,解决此类问题需要系统化的分析和处理方法。以下是详细的解决思路和具体办法,以及不同方法的分析和比较,包括寻求代理、国外技术支持、国内用过的人请教等内容。 1. 了解产品的通信接口和协议 思路…...

.hmallox勒索病毒解密方法|勒索病毒解决|勒索病毒恢复|数据库修复
导言: 在当今数字化时代,勒索病毒已经成为网络安全的一大威胁,其中包括了最近出现的.hmallox勒索病毒。这类恶意软件不仅能够对计算机系统进行加密,还会要求用户支付赎金以换取解密密钥,给个人用户和企业带来了严重的…...

Redis发布、订阅模式(Pub/Sub)详解
Redis发布、订阅模式(PUB-SUB)详解 Redis的发布订阅(Pub/Sub)机制是一种消息通信模式,用于消息的广播。它允许多个客户端订阅(Subscribe)特定的频道(Channel),…...
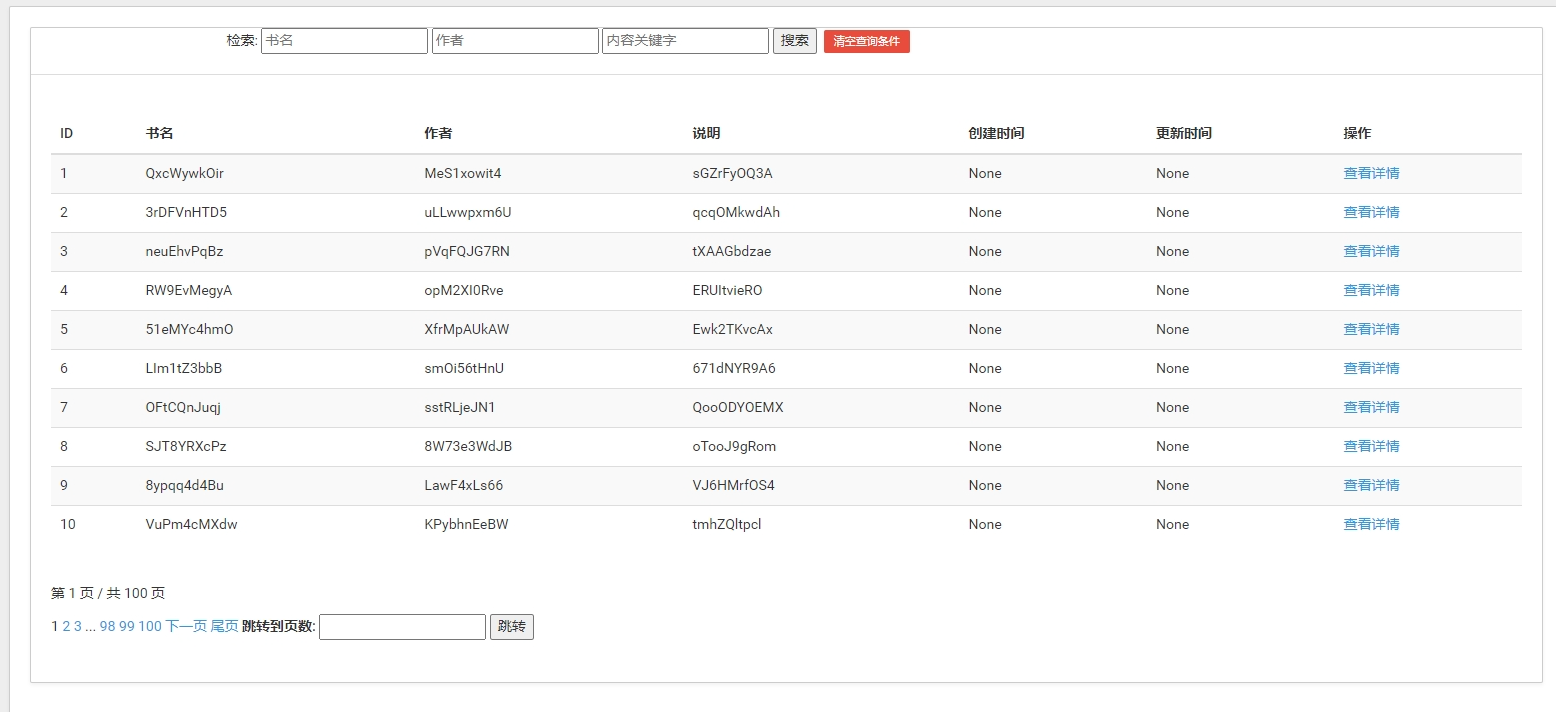
Django-开发一个列表页面
需求 基于ListView,创建一个列表视图,用于展示"BookInfo"表的信息要求提供分页提供对书名,作者,描述的查询功能 示例展示: 1. 数据模型 models.py class BookInfo(models.Model):titlemodels.CharField(verbose_name"书名",max_length100)authormode…...
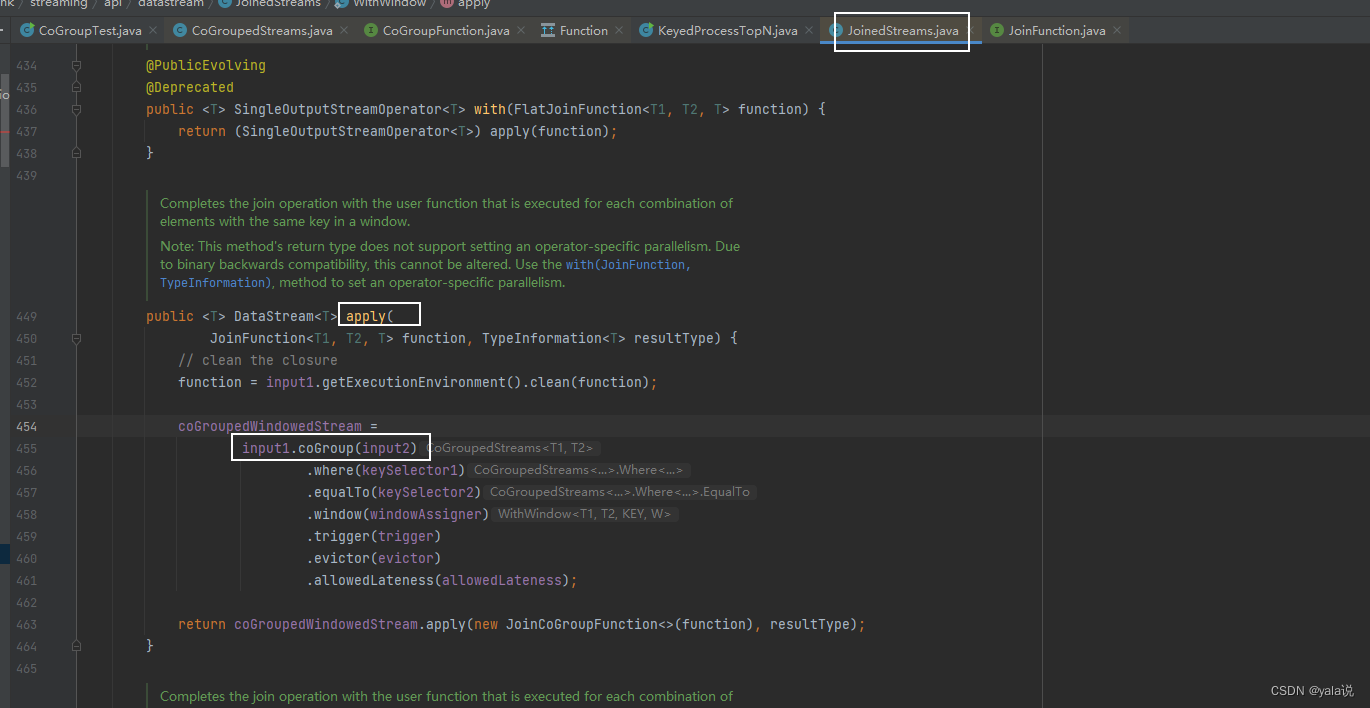
flink 处理函数和流转换
目录 处理函数分类 概览介绍 KeydProcessFunction和ProcessFunction 定时器TimeService 窗口处理函数 多流转换 分流-侧输出流 合流 联合(Uniion) 连接(connect) 广播连接流(BroadcatConnectedStream…...
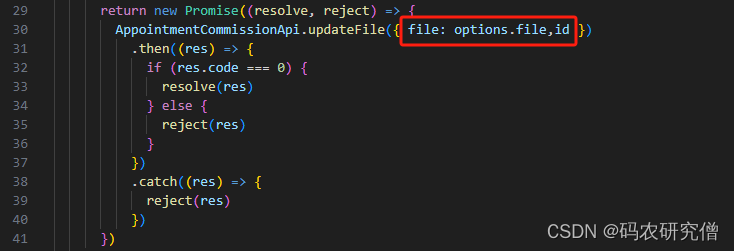
详细分析Springmvc中的@ModelAttribute基本知识(附Demo)
目录 前言1. 注解用法1.1 方法参数1.2 方法1.3 类 2. 注解场景2.1 表单参数2.2 AJAX请求2.3 文件上传 3. 实战4. 总结 前言 将请求参数绑定到模型对象上,或者在请求处理之前添加模型属性 可以在方法参数、方法或者类上使用 一般适用这几种场景: 表单…...

和利时SIS安全系统模块SGM210 SGM210-A02
和利时SIS安全系统模块SGM210 SGM210-A02 阀门定位器:(福克斯波罗, YTC,山武) PLC:(西门子,施耐德,ABB,AB,三菱,欧姆龙) 泵阀:(力士…...
浔川3样AI产品即将上线!——浔川总社部
浔川3样AI产品即将上线! 浔川AI翻译v3.0 即将上线! 浔川画板v5.1 即将上线! 浔川AI五子棋v1.4 即将上线! 整体通告详见:浔川AI五子棋(改进(完整)版1.3)——浔川python社…...

小阿轩yx-MySQL索引、事务
小阿轩yx-MySQL索引、事务 MySQL 索引介绍 是一个排序的列表,存储着索引的值和包含这个值的数据所在行的物理地址数据很多时,索引可以大大加快查询的速度使用索引后可以不用扫描全表来定位某行的数据而是先通过索引表找到该行数据对应的物理地址然后访…...

搞定求职难题:工作岗位列表+简历制作工具 | 开源专题 No.75
SimplifyJobs/New-Grad-Positions Stars: 8.5k License: NOASSERTION 这个项目是一个用于分享和跟踪美国、加拿大或远程职位的软件工作机会列表。该项目的核心优势和关键特点如下: 自动更新新岗位信息便捷地提交问题进行贡献提供一键申请选项 BartoszJarocki/cv…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
