【编程基础】009.输入两个正整数m和n,求其最大公约数和最小公倍数。
最大公约数与最小公倍数
题目描述
输入两个正整数m和n,求其最大公约数和最小公倍数。
输入格式
两个整数
输出格式
最大公约数,最小公倍数
样例输入
5 7
样例输出
1 35
题目思路
在这里我们用m表示较大的那个数,n表示较小的数。求最大公约数也即是求能被m和n 整除的最大数。gcd(m,n) 表示m 和n 的最大公约数。根据辗转相除法可知gcd(m,n)=gcd(n,m%n),具体证明过程如下:
gcd(m,n)=gcd(n,mmodn)\operatorname{gcd}(m, n)=\operatorname{gcd}(n, m \bmod n)gcd(m,n)=gcd(n,mmodn) (不妨设 m>nm>nm>n 且 r=mmodn,r≠0r=m \bmod n, r \neq 0r=mmodn,r=0 )
mmm 可以表示成 m=kn+r(m,n,k,rm=k n+r(m, n, k, rm=kn+r(m,n,k,r 皆为正整数, 且 r<n)r<n)r<n) ,则 r=mmodnr=m \bmod nr=mmodn, 假设 ddd 是 m,nm, nm,n 的一个公约数,即 mmm 和 nnn 都可以被 ddd 整除。
而 r=m−knr=m-k nr=m−kn,两边同时除以 ddd ,可得:
rd=md−knd=h\frac{r}{d}=\frac{m}{d}-\frac{k n}{d}=h dr=dm−dkn=h
由等式右边可知 hhh 为整数( ddd 是 mmm 和 nnn 的公约数, knk nkn 是 nnn 的整倍数,所以 knd\frac{k n}{d}dkn 也应该是整数),所 以我们得出 ddd 也为 mmm 和 nnn 的余数的公约数即 ddd 是 n,mmodnn , m \bmod nn,mmodn 的公约数
至此,我们得知,如果一个数是两个数的公约数,那么,它也是这两个数的余数和较小数公约数。
假设 ddd 是 (n,mmodn)(n, m \bmod n)(n,mmodn) 的任意一个公约数,则 ddd 是 nnn 的公约数, ddd 是 (m−kn)(m-k n)(m−kn) 的公约数, kkk 是一个整数,
我们假设 n=xd,m−kn=ydn=x d, m-k n=y dn=xd,m−kn=yd 其中 x,yx, yx,y 是正整数,根据上面的推断可得:
m=yd+knm=y d+k n m=yd+kn
两边同时除以 ddd ,得
md=y+knd\frac{m}{d}=y+\frac{k n}{d} dm=y+dkn
由已知可得 yyy 为正整数, ddd 是 mmm 的公约数, knd\frac{k n}{d}dkn 也肯定是正整数,故得 ddd 为 mmm 的公约数.
因为 ddd 既是 nnn 的公约数又是 mmm 的公约数了,
所以证出 (m,n)(m, n)(m,n) 和 (n,mmodn)(n, m \bmod n)(n,mmodn) 的公约数是一样的,其最大公约数也必然相等。
所以求m和n的最大公约数,等价于求n 和m%n的最大公约数,用图来表示即不断地用n去填充 m表示的区域,接着赋值n=m%n,m=n 重复上述操作直到m%n==0,则n就是m和n的最大公约数。

AC代码(C语言)
#include<stdio.h>
int gcd(int m,int n){ int t;if(n>m){//令m>nt=n;n=m;m=t;}if(m%n==0) return n;return gcd(n,m%n);
}
int main(){int m,n;scanf("%d%d",&m,&n);int gc=gcd(m,n);int cm=(m/gc)*(n/gc)*gc;printf("%d\n%d\n",gc,cm);return 0;
}
相关文章:

【编程基础】009.输入两个正整数m和n,求其最大公约数和最小公倍数。
最大公约数与最小公倍数 题目描述 输入两个正整数m和n,求其最大公约数和最小公倍数。 输入格式 两个整数 输出格式 最大公约数,最小公倍数 样例输入 5 7 样例输出 1 35 题目思路 在这里我们用m表示较大的那个数,n表示较小的数。求…...

Golang错误处理
介绍 如果你写过任何 Go 代码,你可能遇到过内置error类型。Go 代码使用error值来指示异常状态。例如,函数在打开文件失败时os.Open返回一个非零值。error func Open(name string) (file *File, err error) 下面的代码用于os.Open打开一个文件。如果发生错误,它会调用log.Fat…...

English Learning - L2 语音作业打卡 复习对比 [ɑ:] [æ] Day18 2023.3.10 周五
English Learning - L2 语音作业打卡 复习对比 [ɑ:] [] Day18 2023.3.10 周五💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [ɑ:]…...

LabVIEW中以编程方式获取VI克隆名称
LabVIEW中以编程方式获取VI克隆名称演示如何以编程方式获取VI的名称或克隆名称。如果VI作为顶级VI运行,则将显示VI的名称。如果VI在主VI中用作子VI,它将返回克隆的名称。在项目开发过程中,有时需要获取VI的名称。在此示例中,实现了…...
的使用原理以及InnoDb的优化策略)
Mysql count(*)的使用原理以及InnoDb的优化策略
Mysql count的原理你真的了解吗?1、数据库引擎的区别2、InnoDB中count的使用3、innodb对select(\*)的优化/为什么select(\*)通过非聚集索引效率要高于聚集索引面试问到说“你觉得count(*) 的效率怎么样?”,一般回复innodb对count(*)进行优化后…...

一文入门HTML+CSS+JS(样例后续更新)
一文入门HTMLCSSJS(样例后续更新)前言HTML,CSS和JS的关系HTMLhead元素titlelinkmetabody元素设置网页正文颜色与背景颜色添加网页背景图片设置网页链接文字颜色设置网页边框文字与段落标记普通文字的输入对文字字体的设置 font使用文字的修饰…...
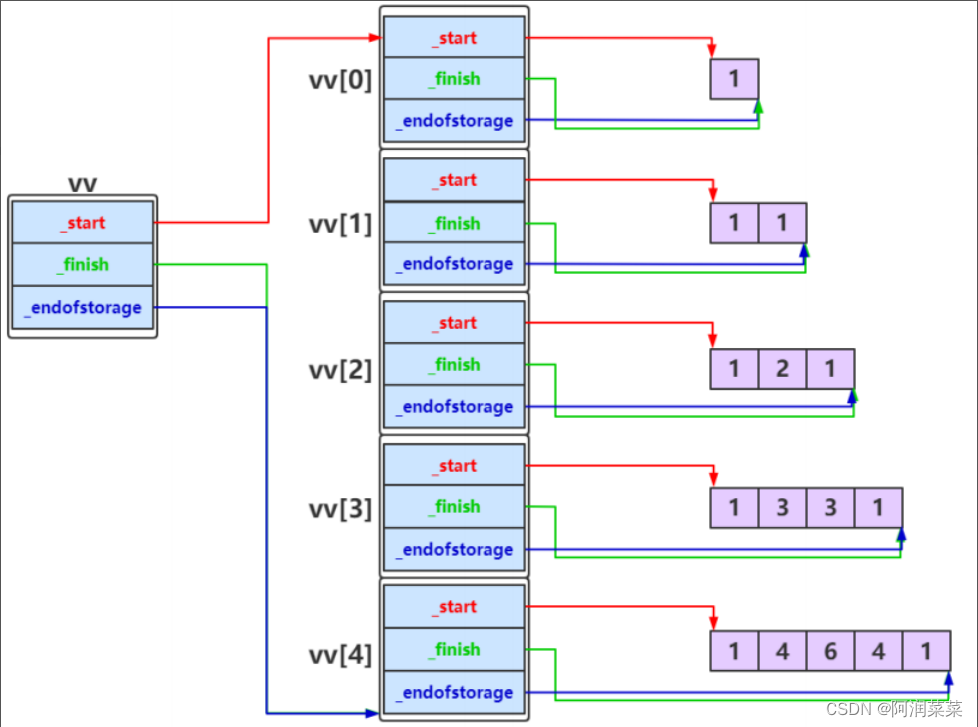
【STL】Vector剖析及模拟实现
✍作者:阿润菜菜 📖专栏:C vector的常用接口 首先贴上:vector的文档介绍,以备查阅使用。 vector的基本框架: vector的成员变量分别是空间首部分的_start指针和最后一个元素的下一个位置的_finish指针,以…...

数据库建表的一些技巧
文章目录 1.名字1.1 见名知意1.2 大小写1.3 分隔符1.4 表名1.5 字段名称1.6 索引名2.字段类型3.字段长度4.字段个数5. 主键6.存储引擎7. NOT NULL8.外键9. 索引10.时间字段11.金额字段12.唯一索引13.字符集14. 排序规则15.大字段总结如果我们在建表的时候不注意细节,等后面系统…...
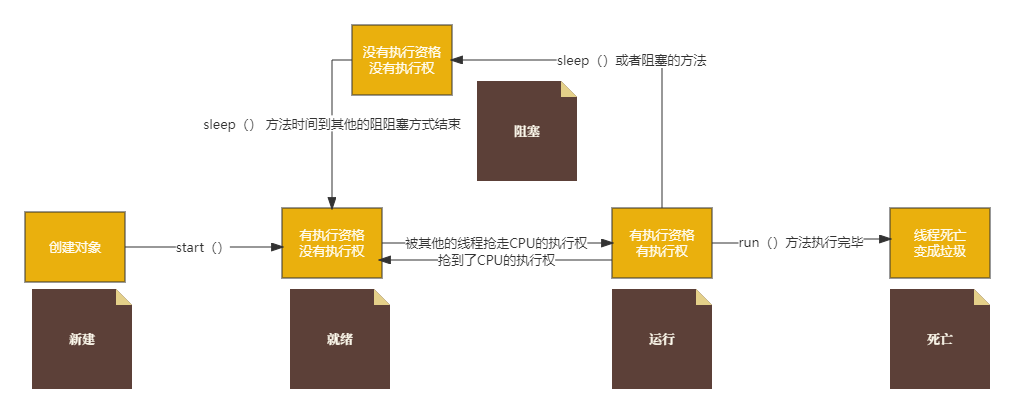
线程(一)
线程 1. 线程 定义:线程是进程的组成部分,不同的线程执行不同的任务,不同的功能模块,同时线程使用的资源师由进程管理,主要分配CPU和内存。 在进程中,线程执行的方式是抢占式执行操作,需要考…...
操作_multi plane 为何能提高闪存速度)
[深入理解SSD系列 闪存实战2.1.8] NAND FLASH Multi Plane Program(写)操作_multi plane 为何能提高闪存速度
前言 上一篇我们介绍了 [深入理解SSD系列 闪存实战2.1.7] NAND FLASH基本编程(写)操作及原理_NAND FLASH Program Operation 源码实现。这只是一次对单个plane 写, 按这样的话, 要先program plane 0 完成后, 再 program plane 1。 如果我偷偷告诉你, 两个 plane 可以一起…...
——第一章知识总结)
计算机网络(第八版)——第一章知识总结
本笔记来源于博主上课所记笔记整理,可能不全,欢迎大家批评指正,如果觉得有用记得点个赞,给博主点个关注...该笔记将会持续更新...整理不易,希望大家多多点赞。 第一章 计算机网络体系结构 1.计算机网络的作用 1.1互…...
Linux学习笔记
前段时间看了网课:https://www.bilibili.com/video/BV1mW411i7Qf?spm_id_from333.337.search-card.all.click&vd_source7b9f1ca2783a4c39a4d640a31e23457e 记了一些笔记,先放到这里,后面慢慢整理: 内存分配:分区…...
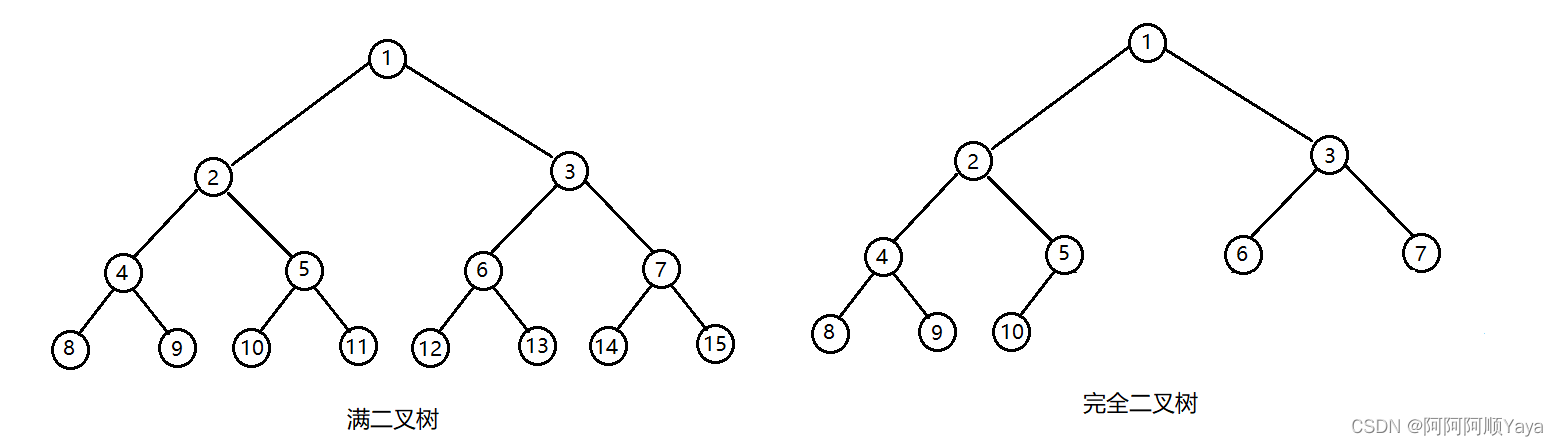
树与二叉树(概念篇)
树与二叉树1 树的概念1.1 树的简单概念1.2 树的概念名词1.3 树的相关表示2 二叉树的概念2.1 二叉树的简单概念2.1.1 特殊二叉树2.2 二叉树的性质2.3 二叉树的存储结构1 树的概念 1.1 树的简单概念 树是一种非线性的数据结构,它是由n(n>0)个有限节点组成的一个具…...
C++回顾(二十五)—— map/multimap容器
25.1 map/multimap的简介 map是标准的关联式容器,一个map是一个键值对序列,即(key,value)对。它提供基于key的快速检索能力。map中key值是唯一的。集合中的元素按一定的顺序排列。元素插入过程是按排序规则插入,所以不能指定插入位置。map的…...

7.3 向量的数量积与向量积
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人! 🌙个人主页:阿芒的主页 ⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学…...

Qt静态扫描(命令行操作)
Qt静态扫描(命令行操作) 前沿: 静态代码分析是指无需运行被测代码,通过词法分析、语法分析、控制流、数据流分析等技术对程序代码进行扫描,找出代码隐藏的错误和缺陷,如参数不匹配,有歧义的嵌…...

【Hadoop】配置文件
Hadoop 配置文件分两类:默认配置文件和自定义配置文件,只有用户想修改某一默认 配置值时,才需要修改自定义配置文件,更改相应属性值 (1)默认配置文件: cd $HADOOP_HOME/share/hadoop common路…...

python进程池
Python进程池是Python标准库中multiprocessing模块提供的一种用于管理进程的方式。它可以使Python程序以并行的方式执行任务,提高程序的运行效率。本篇博客将介绍如何使用Python进程池。 创建进程池 在使用Python进程池之前,我们需要先创建一个进程池对…...
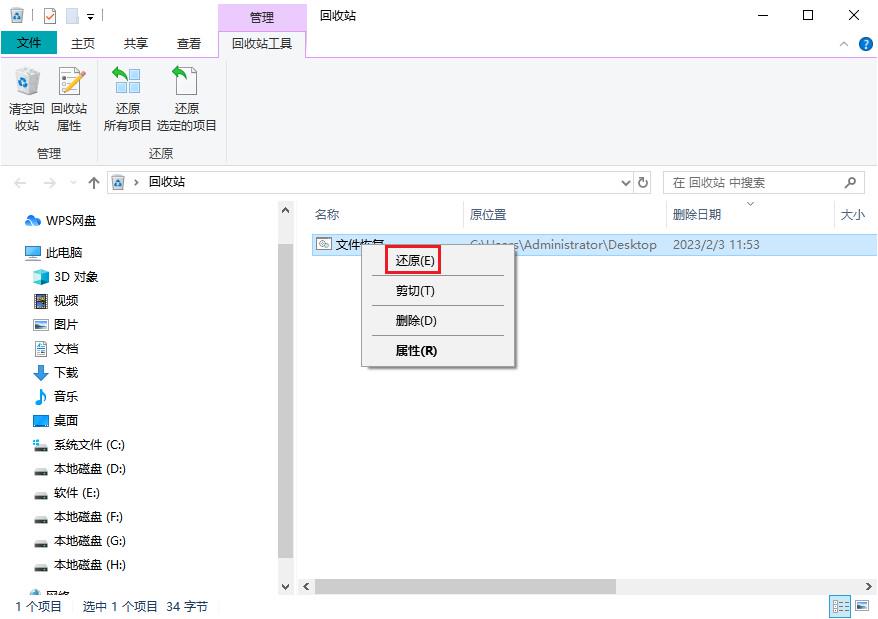
笔记本固态盘数据丢失怎么办?笔记本固态盘怎么恢复数据
如果笔记本固态盘数据丢失怎么办?笔记本固态盘怎么恢复数据?下面将为大家详细地介绍一下笔记本固态硬盘数据恢复的三种实用方法,希望对大家有所帮助。一、简单恢复方法笔记本固态硬盘数据删除以后,较为简单直接的恢复方法就是从回…...
堆的结构与实现
堆的结构与实现二叉树的顺序结构堆的概念及结构堆的实现堆的创建向上调整建堆向下调整建堆堆的操作链接二叉树的顺序结构 堆其实是具有一定规则限制的完全二叉树。 普通的二叉树是不太适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树会更适合使用顺…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
