# 音频处理4_傅里叶变换
1.离散傅里叶变换
对于离散时域信号 x[n]使用离散傅里叶变换(Discrete Fourier Transform, DFT)进行频域分析。
DFT 将离散信号 x[n] 变换为其频谱表示 X[k],定义如下:
X [ k ] = ∑ n = 0 N − 1 x [ n ] e − j 2 π k n N X[k] = \sum_{n=0}^{N-1} x[n]e^{-j\frac{2\pi kn}{N}} X[k]=∑n=0N−1x[n]e−jN2πkn
1.1 共轭对称性
对于实值信号,其离散傅里叶变换(DFT)的结果在频谱上是共轭对称性(Conjugate Symmetry)
复共轭:实数相同,虚数取反
z = a + bi, 那么 \overline{z} = a - bi
1.2 奈奎斯特频率
奈奎斯特频率(Nyquist frequency)指在采样过程中,能够精确还原原始信号的最高频率。根据奈奎斯特定理,为了正确地重建一个信号,采样频率必须至少是信号中最高频率的两倍。
因此,奈奎斯特频率就是采样频率的一半。如果信号的频谱超过了奈奎斯特频率,就会出现混叠(aliasing)现象,导致采样后的信号无法正确还原原始信号。
典型的人类语音频率范围大约在0 Hz到4 kHz之间,主要能量集中在0 Hz到2.5 kHz。因此,为了捕捉和处理语音信号的主要频率成分,通常选择的采样频率是略大于这个最高频率(如8 kHz)。
1.3 混叠(aliasing)现象
即采样频率低于信号中最高频率的两倍,就会导致频域中的信号成分发生错位和重叠(表现为失真),从而无法正确地重建原始信号
如果采样频率低于最高频率的两倍,那么高于奈奎斯特频率的信号成分会“折叠”到采样频率范围内的其他频率位置上。
当信号频率超过了奈奎斯特频率时,它在采样后的频域中将被错误地解释为低于奈奎斯特频率的频率,这会导致信号在频域中产生额外的频率能量,这些能量是原始信号频率的镜像(或折叠)。
2.快速傅里叶变换(FFT)
FFT利用分治策略将离散傅里叶变换(DFT)分解为更小规模的DFT计算。将长度为 N 的序列分成长度为
N/2 的两个子序列,然后递归地应用FFT算法计算这两个子序列的DFT,最后将结果合并为原始序列的DFT。
- Scipy的FFT用于可视化频域图
# 使用 scipy.fftpack.fft 计算 FFT
fft_result = fft(signal)# 计算频率轴
freqs = np.fft.fftfreq(len(signal), d=t[1] - t[0])
3.短时傅里叶变换(STFT)
短时傅里叶变换(Short-Time Fourier Transform, STFT)用于画时频谱,
是一种将信号分解到时间-频率域的方法,
参数如下:
input (Tensor):
* 输入信号,可以是 1D 或 2D 张量。
* 如果是 1D 张量,则表示单个信号序列。
* 如果是 2D 张量,第一维表示信号的批次(batch),第二维表示每个信号的时间步。n_fft (int):
* 每个窗口的 FFT 点数。
* 通常是一个大于等于 win_length 的值。这个参数决定了频域分辨率。hop_length (int, optional):
* 窗口之间的跳跃长度(即窗口之间的距离)。
* 默认值为 win_length // 2,即窗口重叠一半。win_length (int, optional):
* 每个窗口的长度。
* 默认值为 n_fft, 大于n_fft, 则需要填充窗口剩余样本点。window (Tensor, optional):
* 窗函数,用于加窗处理,以提升频谱的平滑度。
* 通常使用汉宁窗(Hann window)或汉明窗(Hamming window)。
* 默认值为一个全 1 的窗函数。center (bool, optional):
* 如果为 True(默认值),则在信号的两端各加上 n_fft // 2 个零,以确保每个时间点都有一个完整的窗口。pad_mode (str, optional):
* 填充模式,当 center 为 True 时使用。
* 可以是 'constant', 'reflect' 等。默认值为 'reflect'。normalized (bool, optional):
* 如果为 True,则返回的 STFT 会进行归一化处理。onesided (bool, optional):
* 如果为 True(默认值),则返回的 STFT 只包含非负频率部分,这在处理实数信号时是有用的。return_complex (bool, optional):
* 如果为 True,则返回复数类型的结果。否则,返回一个两通道的实数张量,其中一个通道是实部,另一个通道是虚部。4.代码样例
一个信号由两个信号叠加:
signal = np.sin(2 * np.pi * 5 * t) + np.sin(2 * np.pi * 50 * t)
上图为stft, 下图为fft
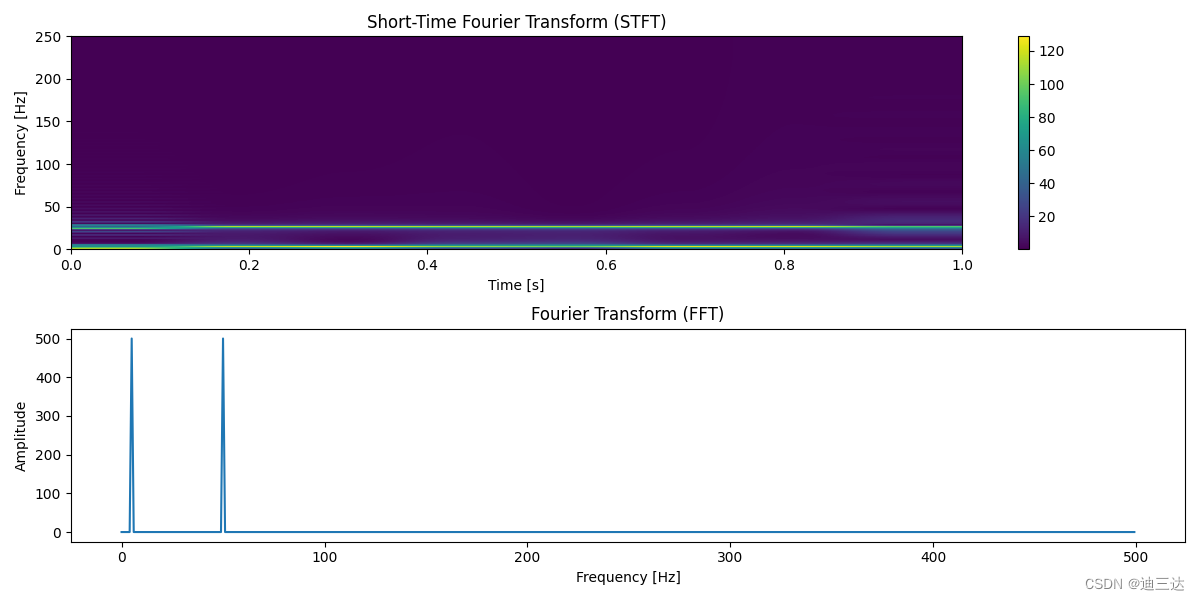
代码在Github_Link
相关文章:

# 音频处理4_傅里叶变换
1.离散傅里叶变换 对于离散时域信号 x[n]使用离散傅里叶变换(Discrete Fourier Transform, DFT)进行频域分析。 DFT 将离散信号 x[n] 变换为其频谱表示 X[k],定义如下: X [ k ] ∑ n 0 N − 1 x [ n ] e − j 2 π k n N X[k]…...

提升网络速度的几种有效方法
在数字化时代,网络速度对于我们的日常生活和工作至关重要。无论是观看高清视频、在线游戏,还是进行视频会议,快速稳定的网络连接都是不可或缺的。如果你发现自己当前的网络速度不尽如人意,那么不妨尝试以下几种方法来提升它。 升…...
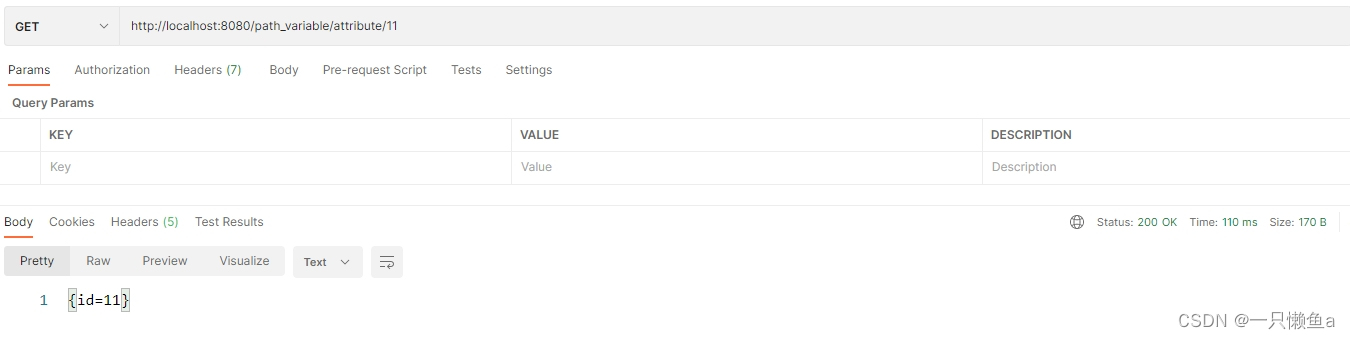
@PathVariable注解的使用及源码解析
前言 PathVariable 注解是我们进行JavaEE开发,最常见的几个注解之一,这篇博文我们以案例和源码相结合,帮助大家更好的了解PathVariable 注解 使用案例 1.获取 URL 上的值 RequestMapping("/id/{id}") public Object getId(Path…...

服务器配置重点看哪些参数
对服务器有需求时,应重点考虑以下几个关键参数,以下仅供参考: 处理器(CPU):包括CPU的品牌(如Intel或AMD)、型号、核心数、线程数、主频和缓存大小。核心数越多,处理并发请…...

WSL Ubuntu 如何设置中文语言?
本章教程,主要介绍如何在WSL Ubuntu 如何设置中文语言。 操作系统:Windows 10 Pro 64 WSL子系统:Ubuntu 20.04 LTS 一、安装中文语言包 sudo apt install language-pack-zh-hans二、设置中文语言 sudo dpkg-reconfigure locales选择en_US.UTF-8 和 zh_CN.UTF-8 选择zh_CN.…...

「51媒体」政企活动媒体宣发如何做?
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 媒体宣传加速季,100万补贴享不停,一手媒体资源,全国100城线下落地执行。详情请联系胡老师。 政企活动媒体宣发是一个系统性的过程,需要明确…...

K近邻回归原理详解及Python代码示例
K近邻回归原理详解 K近邻回归(K-Nearest Neighbors Regression, KNN)是一种基于实例的学习算法,用于解决回归问题。它通过找到输入数据点在特征空间中最相似的K个邻居(即最近的K个数据点),并使用这些邻居的…...
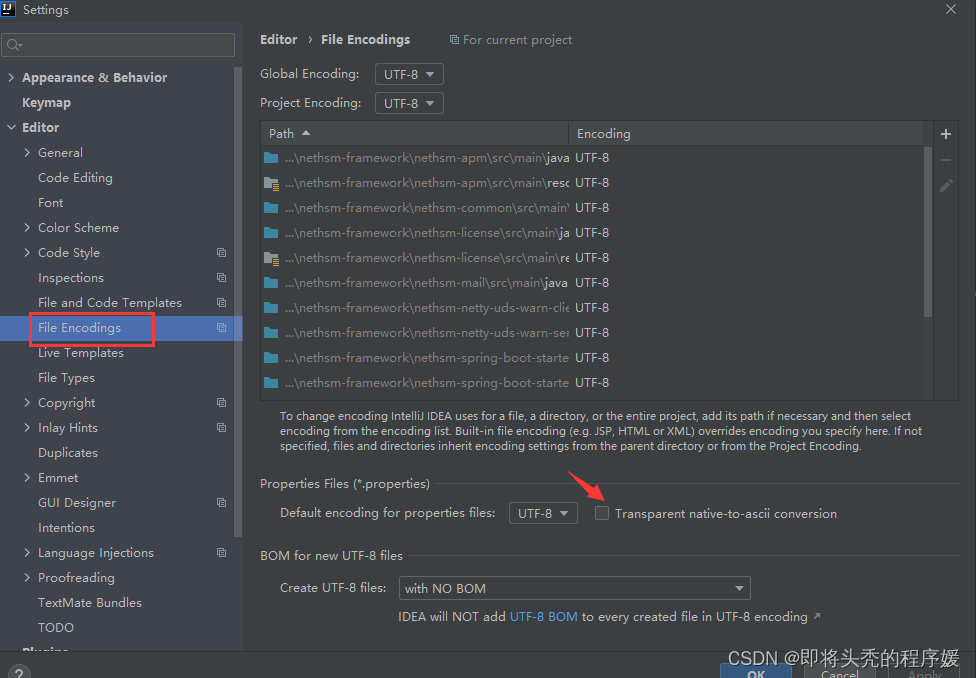
idea 开发工具properties文件中的中文不显示
用idea打开一个项目,配置文件propertise中的中文都不展示,如图: 可修改idea配置让中文显示: 勾选箭头指向的框即可,点击应用保存,重新打开配置文件,显示正常...

让DroidVNC-NG支持中文输入
DroidVNC-NG支持控制端输入内容,但是仅支持英文字符,如果需要控制输入法软键盘输入中文的话就没办法了,经过摸索找到了解决办法。 这个解决办法有个条件就是让DroidVNC-NG成为系统级应用(这个条件比较苛刻)ÿ…...

android dialog 显示时 activity 是否会执行 onPause onStop
当一个 Android Dialog 显示时,当前 Activity 通常不会执行 onPause 或 onStop 方法。Dialog 是附加到 Activity 上的一个窗口,它不会中断或替换当前的 Activity,因此 Activity 的生命周期方法 onPause 和 onStop 不会被调用。 然而…...
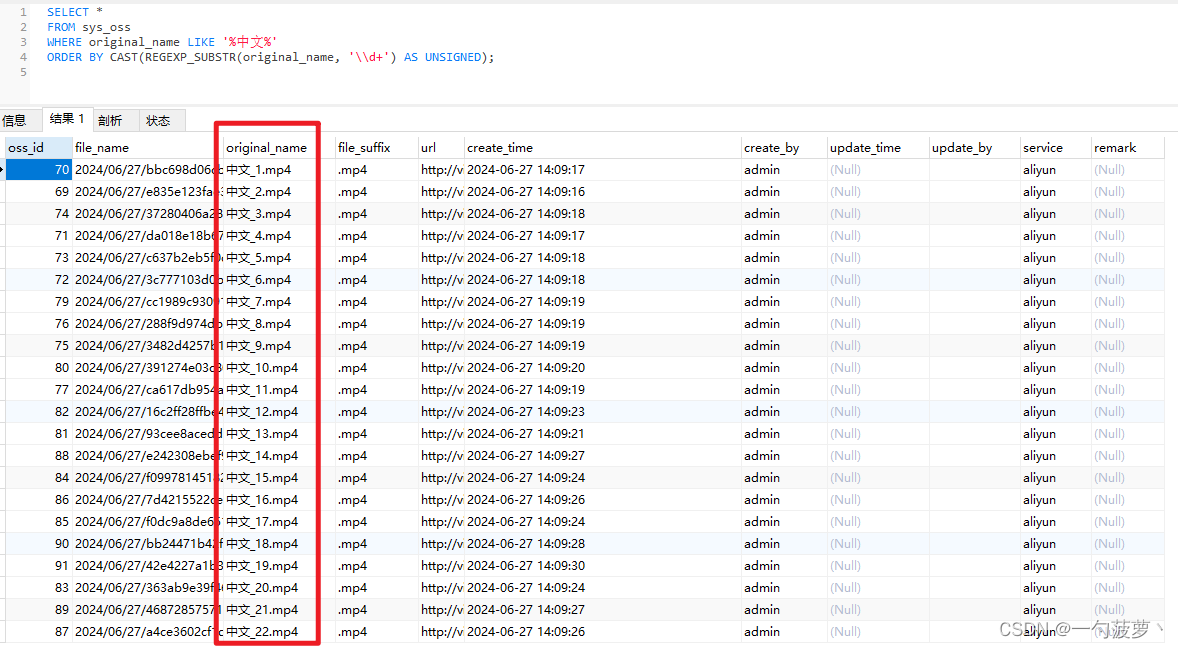
如何在MySQL中按字符串中的数字排序
在管理数据库时,我们经常遇到需要按嵌入在字符串中的数字进行排序的情况。这在实际应用中尤为常见,比如文件名、代码版本号等字段中通常包含数字,而这些数字往往是排序的关键。本文将详细介绍如何在MySQL中利用正则表达式提取字符串中的数字并…...
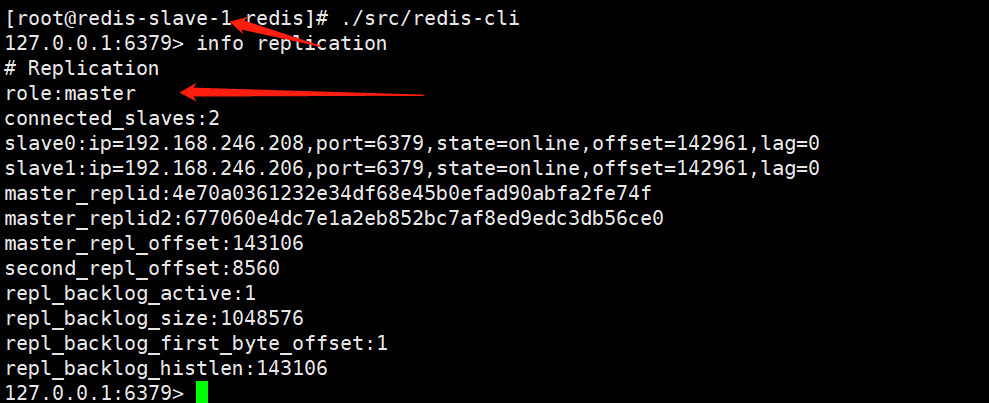
memcacheredis构建缓存服务器
Memcached&Redis构建缓存服务器 前言 许多Web应用都将数据保存到 RDBMS中,应用服务器从中读取数据并在浏览器中显示。但随着数据量的增大、访问的集中,就会出现RDBMS的负担加重、数据库响应恶化、 网站显示延迟等重大影响。Memcached/redis是高性能…...
Linux基础- 使用 Apache 服务部署静态网站
目录 零. 简介 一. linux安装Apache 二. 创建网页 三. window访问 修改了一下默认端口 到 8080 零. 简介 Apache 是世界使用排名第一的 Web 服务器软件。 它具有以下一些显著特点和优势: 开源免费:可以免费使用和修改,拥有庞大的社区支…...
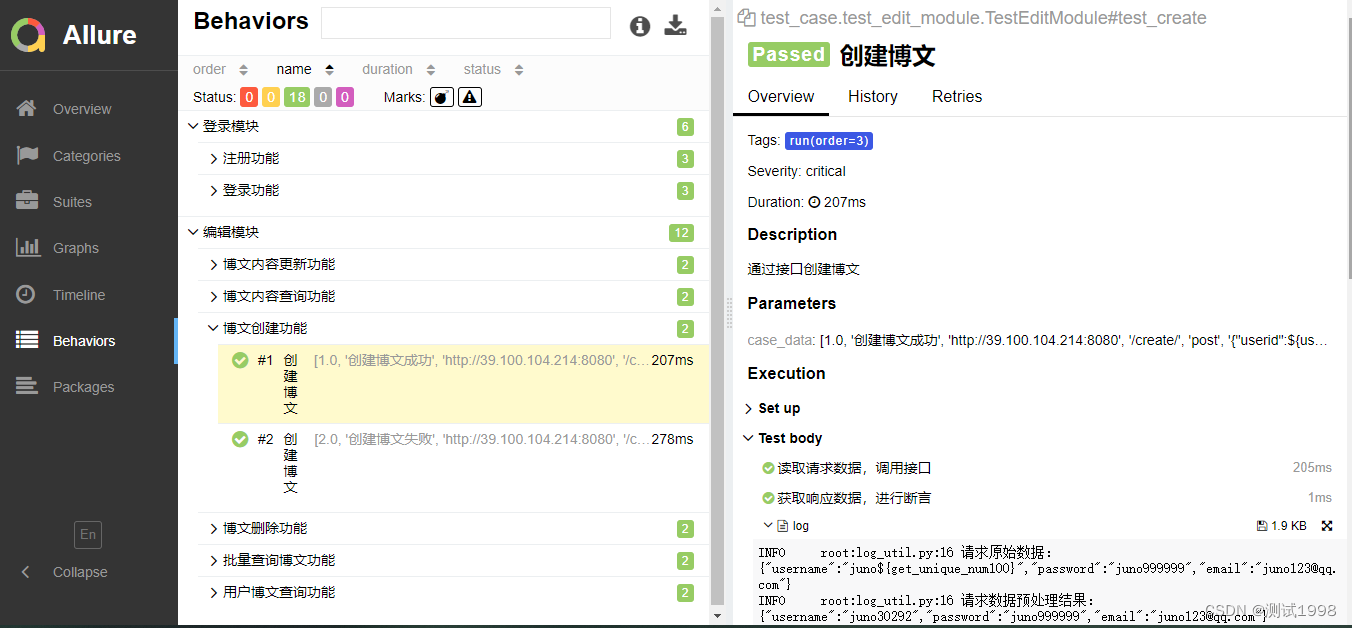
接口自动化测试框架实战(Pytest+Allure+Excel)
🍅 视频学习:文末有免费的配套视频可观看 🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 1. Allure 简介 Allure 框架是一个灵活的、轻量级的、支持多语言的测试报告工具,它不…...

如何预防和处理他人盗用IP地址?
IP地址的定义及作用 解释 IP 地址在互联网中的作用。它是唯一标识网络设备的数字地址,类似于物理世界中的邮政地址。 1、IP地址盗窃的定义 解释一下什么是IP地址盗用,即非法使用他人的IP地址或者伪造IP地址的行为,这种行为可能引发法律和安…...
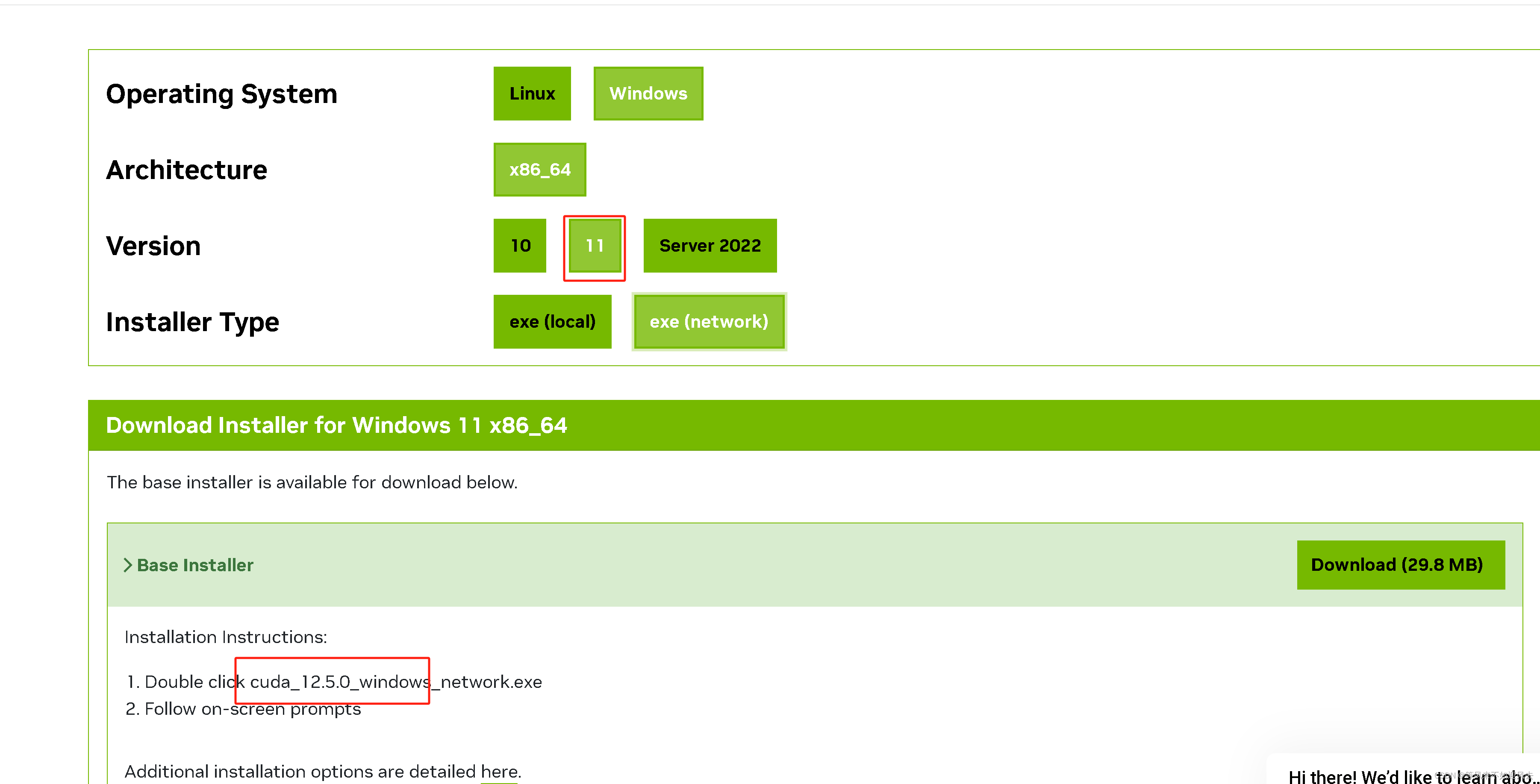
【ai】李沐 动手深度学学v2 环境安装:anaconda3、pycharm、d2
cuda-toolkit cuda_12.5.0_windows_network.exe 官方课程网站 第二版资源下载release版本 pycharm版本 李沐 【动手学深度学习v2 PyTorch版】 课程笔记 CUDA 选择11, 实际下载 12.5.0...

前后端分离对软件行业及架构设计的影响
在软件开发领域,前后端分离是一种越来越流行的架构设计模式。这种方法将用户界面(前端)与服务器逻辑(后端)分离开来,允许它们独立开发、测试和部署。本文将探讨前后端分离对软件行业和架构设计的影响&#…...

深入解析Dubbo架构层次
什么是Dubbo? Dubbo是阿里巴巴开源的一款高性能优秀的服务框架,致力于提供高性能和透明化的 RPC 远程服务调用方案,以及 SOA 服务治理方案。它的主要功能包括: 远程通信:提供高效的远程通信能力。负载均衡࿱…...

关于GPIO的上拉、下拉,无上下拉
1.GPIO_PULLUP(上拉) 作用和原理 作用:上拉模式会在GPIO引脚和电源电压(Vcc)之间连接一个内部上拉电阻。原理:当引脚配置为输入模式时,如果引脚没有连接到其他外部电路,内部上拉电…...

Python 语法基础二
7.常用内置函数 执行这个命令可以查看所有内置函数和内置对象(两个下划线) >>>dir(__builtins__) [__class__, __contains__, __delattr__, __delitem__, __dir__, __doc__, __eq__, __format__, __ge__, __getattribute__, __getitem__, __gt…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
