2023年中国高校计算机大赛-团队程序设计天梯赛(GPLT)上海理工大学校内选拔赛(同步赛) A — E
2023年中国高校计算机大赛-团队程序设计天梯赛(GPLT)上海理工大学校内选拔赛(同步赛)
文章目录
- A -- A Xor B Problem
- 题目分析
- code
- B -- 吃苹果
- 题目分析
- code
- C -- n皇后问题
- 题目分析
- code
- D -- 分苹果
- 题目分析
- code
- E -- 完型填空
- 题目分析
- code
A – A Xor B Problem
题目分析
只有相同数字异或结果才为零,统计一下相同数字出现的次数,排列组合即可。
根据样例来看,自身与自身是可以成为一对数字的。
code
#include<bits/stdc++.h>
#define int long longusing namespace std;const int N = 1010;int n, m, k, t;
int a[N];
map<int, int>q;signed main()
{cin >> n;for(int i = 1; i <= n; i ++){cin >> a[i];q[a[i]] ++;}int ans = 0;for(auto &[k, v] : q){if(v >= 2) ans += v * v;else ans ++;}cout << ans << "\n";;return 0;
}
B – 吃苹果
题目分析
可以通过按照早上和晚上吃苹果愉悦值得差值来排序,差值越大得越优先被处理贡献值越大。
code
#include<bits/stdc++.h>
#define int long longusing namespace std;const int N = 1e5 + 10;int n, m, k, t;
bool st[N];struct node
{int l, r;
}q[N];bool cmp(node a, node b)
{return abs(a.l - a.r) > abs(b.l - b.r);
}signed main()
{cin >> n >> k;for(int i = 1; i <= n; i ++){int u, v;cin >> u >> v;q[i] = {u, v};}sort(q + 1, q + n + 1, cmp);int ans = 0;int r1 = n - k, r2 = k;for(int i = 1; i <= n; i ++){if(q[i].l > q[i].r){if(r1){ans += q[i].l;r1 --;}else ans += q[i].r, r2 --;}else{if(r2){ans += q[i].r;r2 --;}else ans += q[i].l, r1 --;}}cout << ans << "\n";return 0;
}
C – n皇后问题
题目分析
每输入一个点判断其八个方向上是否已经被放过即可,不过判断时暴力手法得判断会超时,我们可以通过判断是否在一条直线上的方式来判断会不会冲突。
横向和纵向的比较简单,问题是处理两个对角线。两个对角线为y=x+a和y=-x+b,可以通过x和y来看常数是否相同从而判断是否在一条直线上。
code
#include<bits/stdc++.h>
using namespace std;const int N = 1e7 + 10;int n, m, k, t;bool row[N], col[N], dg[N], udg[N];bool get(int x, int y)
{if(!row[x] && !col[y] && !dg[x + y] && !udg[n - x + y]){row[x] = col[y] = dg[x + y] = udg[n - x + y] = true;return true;}return false;
}signed main()
{scanf("%d%d", &n, &t);while(t --){int x, y;scanf("%d%d", &x, &y);if (get(x, y)) puts("Yes");else puts("No");}return 0;
}
D – 分苹果
题目分析
可以看作两个木棒把一个桌面分成了四个部分,带入点坐标根据数值得结果可以判断在哪个部分。
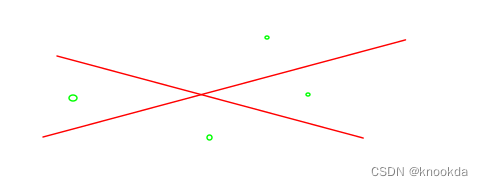
code
#include <bits/stdc++.h>
#define int long longusing namespace std;int a[5];
int n, m, k, t;
int Ae, Be, Ce;
int Ar, Br, Cr;signed main()
{cin >> n;cin >> Ae >> Be >> Ce;cin >> Ar >> Br >> Cr;for(int i = 1; i <= n; i ++){int x, y;cin >> x >> y;int ans1 = Ae * x + Be * y + Ce;int ans2 = Ar * x + Br * y + Cr;if(ans1 > 0 && ans2 > 0) a[1]++;else if(ans1 > 0 && ans2 < 0) a[2]++;else if(ans1 < 0 && ans2 > 0) a[3] ++;else if(ans1 < 0 && ans2 < 0) a[4] ++;}sort(a + 1, a + 5);for(int i = 1; i <= 4; i ++) cout << a[i] << " " ;
}
E – 完型填空
题目分析
本体数据范围较小并且分成的情况很多,可以采用动态规划的方法。
集合f[i][j][k][r]表示:A选项选了i个,B选项选了j个,C选项选了k个,D选项选了f个,所得期望的值的集合
根据思考前一个得方法,可以很容易得到状态转移方程。
code
#include<bits/stdc++.h>
#define int long longusing namespace std;const int N = 110;int n, m, k, t;
int a[N], w[N][5];
int f[N][N][N][N];signed main()
{cin >> n;for(int i = 1; i <= n; i ++)for(int j = 1; j <= 4; j ++)cin >> w[i][j];n /= 4;for(int i = 0; i <= n; i ++)for(int j = 0; j <= n; j ++)for(int k = 0; k <= n; k ++)for(int r = 0; r <= n; r ++){if(i > 0)f[i][j][k][r] = max(f[i][j][k][r], f[i - 1][j][k][r] + w[i + j + k + r][1]);if(j > 0)f[i][j][k][r] = max(f[i][j][k][r], f[i][j - 1][k][r] + w[i + j + k + r][2]);if(k > 0)f[i][j][k][r] = max(f[i][j][k][r], f[i][j][k - 1][r] + w[i + j + k + r][3]);if(r > 0)f[i][j][k][r] = max(f[i][j][k][r], f[i][j][k][r - 1] + w[i + j + k + r][4]);}cout << f[n][n][n][n] << "\n";return 0;
}
相关文章:

2023年中国高校计算机大赛-团队程序设计天梯赛(GPLT)上海理工大学校内选拔赛(同步赛) A — E
2023年中国高校计算机大赛-团队程序设计天梯赛(GPLT)上海理工大学校内选拔赛(同步赛) 文章目录A -- A Xor B Problem题目分析codeB -- 吃苹果题目分析codeC -- n皇后问题题目分析codeD -- 分苹果题目分析codeE -- 完型填空题目分析codeA – A…...

一文分析Linux v4l2框架
说明: Kernel版本:4.14 ARM64处理器,Contex-A53,双核 使用工具:Source Insight 3.5, Visio 1. 概述 V4L2(Video for Linux 2):Linux内核中关于视频设备驱动的框架,对上向应用层提供…...
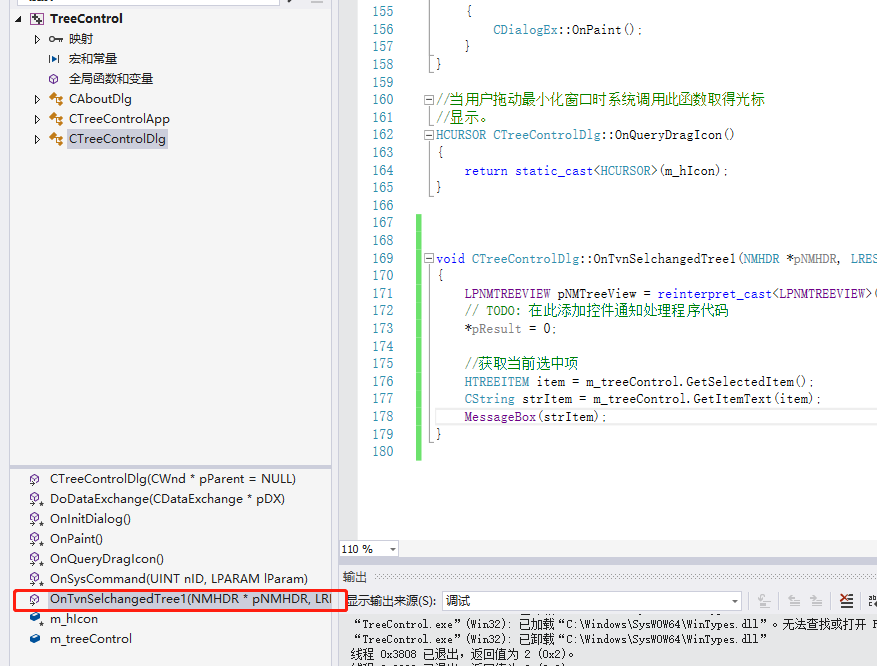
MFC常用控件使用(文本框、编辑框、下拉框、列表控件、树控件)
简介 本文章主要介绍下MFC常用控件的使用,包括静态文本框(Static Text)、编辑框(Edit Control)、下拉框(Combo Box)、列表控件(List Control)、树控件(Tree Control)的使用。 创建项目 我们选择 文件->新建->新建项目,选择MFC程序 选择基于对话…...

13 node 程序后台执行加上 tail 命令, 中断 tail 命令, 同时也中断了 node 程序
前言 呵呵 最近帮朋友解决问题[2022.09.08] 需要启动一个 node 程序, 然后 需要一个 startUp.sh 脚本 然后 反手写了一个过去, 按道理 来说 应该是 后台启动了对应的 node 程序, 然后将 标准输出, 错误输出 输出到 logs/nohup.log 日志文件中, 然后基于 tail 命令 来查看 …...
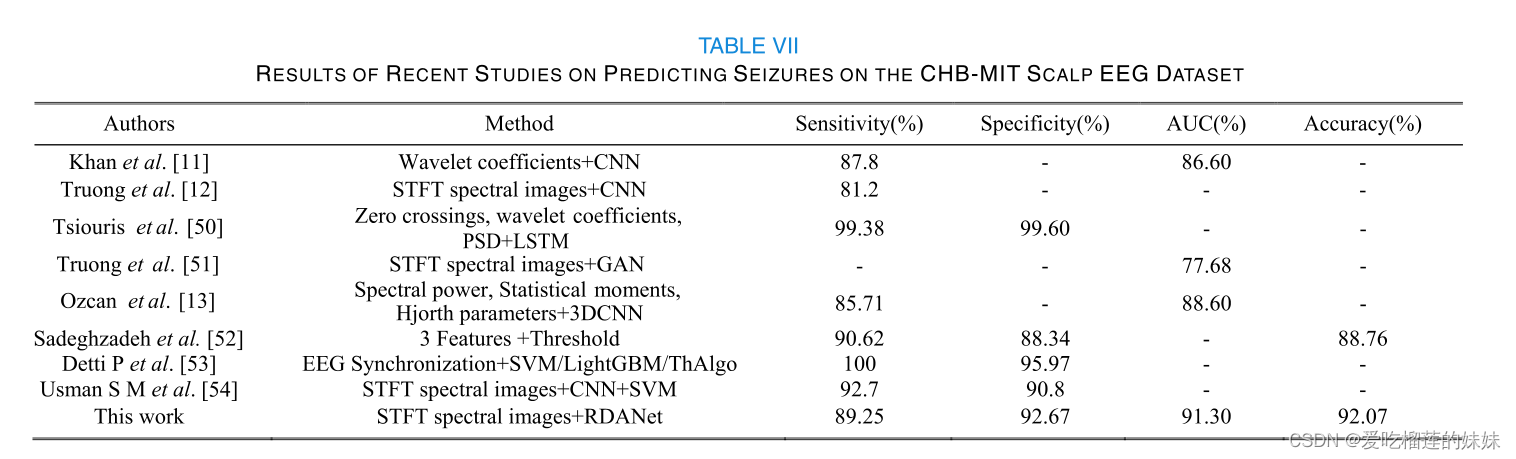
52癫痫发作预测的有效双自注意力残差网络
Effective dual self-attentional residual networks for epileptic seizure prediction 摘要 癫痫发作预测作为慢性脑疾病中最具挑战性的数据分析任务之一,引起了众多研究者的广泛关注。癫痫发作预测,可以在许多方面大大提高患者的生活质量࿰…...

【计算机网络】Tcp IP 面试题相关
互联网协议群(TCP/IP):多路复用是怎么回事? 1.【问题】IPv4 和 IPv6 有什么区别? IPv4 是用 32 位描述 IP 地址,理论极限约在 40 亿 IP 地址; IPv6 是用 128 位描述 IP 地址,IPv6 可…...

【MySQL】MySQL的存储引擎
目录 概念 分类 操作 概念 数据库存储引擎是数据库底层软件组织,数据库管理系统(DBMS)使用数据引擎进行创建、查 询、更新和删除数据。 不同的存储引擎提供不同的存储机制、索引技巧、锁定水平等功能。现在 许多不同的数据库管理系统…...

es6动态模块import()
目录 一、语法说明 二、适用场合 三、注意点 四、示例代码 五、效果 一、语法说明 import命令会被 JavaScript 引擎静态分析,先于模块内的其他语句执行(import命令叫做“连接” binding 其实更合适)。 // 报错 if (x 2) {import MyMod…...
)
【Flask】Jinja2模板(十四)
Jinja2是一个单独的Python包,Flask依赖Jinja2,安装Flask时会自动安装Jinja2。Jinja2可以将数据和模板结合在一起生成动态文本。 一、引入 来看一个最简单的视图函数: app.route(/) def hello_world():return Hello World! 这个…...

Mr. Cappuccino的第49杯咖啡——冒泡APP(升级版)之基于Docker部署Gitlab
冒泡APP(升级版)之基于Docker部署Gitlab基于Docker安装Gitlab登录Gitlab创建Git项目上传代码使用Git命令切换Git地址使用IDE更换Git地址基于Docker安装Gitlab 查看beginor/gitlab-ce镜像版本 下载指定版本的镜像 docker pull beginor/gitlab-ce:11.3.0…...
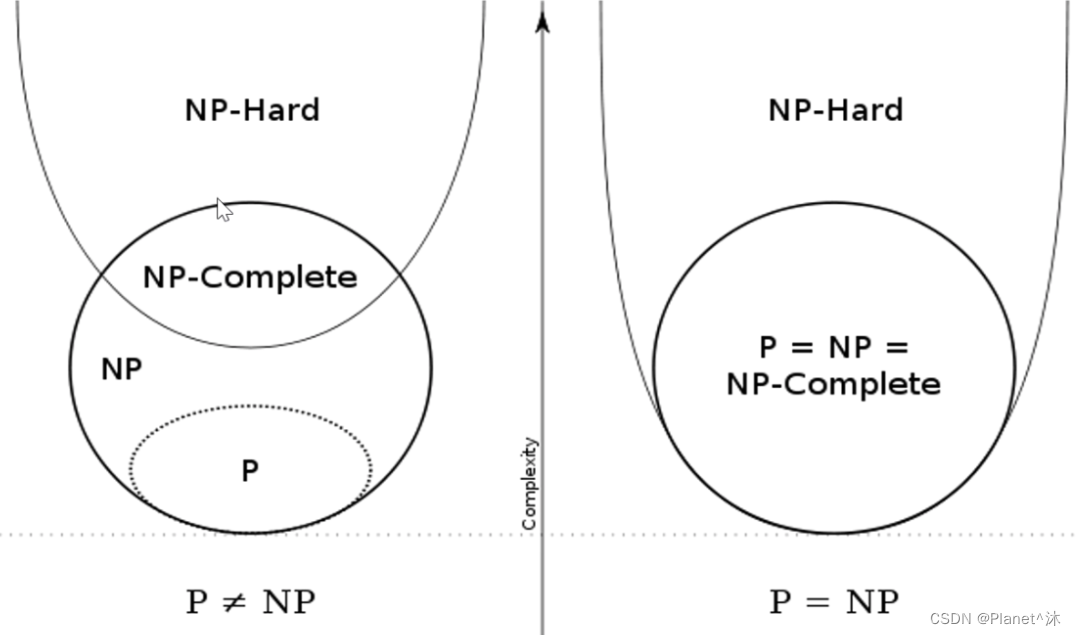
《机器学习》基础概念之【P问题】与【NP问题】
《机器学习》基础概念之【P问题】与【NP问题】 这里写目录标题《机器学习》基础概念之【P问题】与【NP问题】一、多项式&时间复杂度1.1. 多项式1.2.时间复杂度二、P问题 & NP问题2.1. P问题2.2.NP问题2.3.举例理解NP问题-TSP旅行商推销问题三、NP-hard问题&NP-C问题…...

WinRAR安装教程
文章目录WinRAR安装教程无广告1. 下载2. 安装3. 注册4. 去广告WinRAR安装教程无广告 1. 下载 国内官网:https://www.winrar.com.cn/ 2. 安装 双击,使用默认路径: 点击“安装”。 点击“确定”。 点击“完成”。 3. 注册 链接ÿ…...
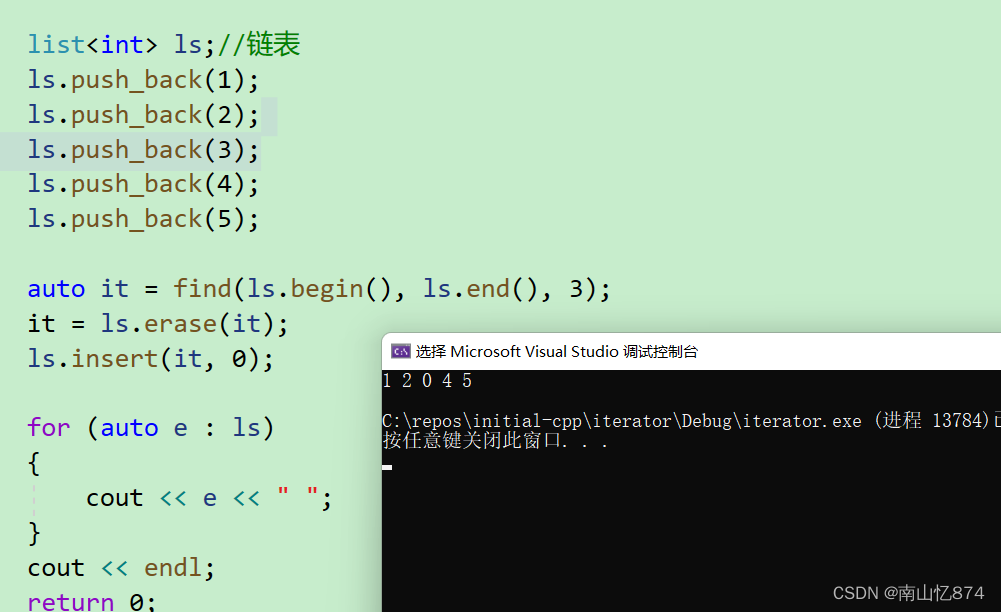
C++:vector和list的迭代器区别和常见迭代器失效问题
迭代器常见问题的汇总vector迭代器和list迭代器的使用vector迭代器list迭代器vector迭代器失效问题list迭代器失效问题vector和list的区别vector迭代器和list迭代器的使用 学习C,使用迭代器和了解迭代器失效的原因是每个初学者都需要掌握的,接下来我们就…...

SpringSecurity如何实现前后端分离
前后端分离模式是指由前端控制页面路由,后端接口也不再返回html数据,而是直接返回业务数据,数据一般是JSON格式。Spring Security默认的表单登录方式,在未登录或登录成功时会发起页面重定向,在提交登录数据时ÿ…...

为ubuntu 18.04添加蓝牙驱动
目录背景方法背景 从网上买的能直接插ubuntu 1804的usb蓝牙太少了,而且还贵。我就直接从JD下单的一个便宜的USB蓝牙,结果插上机器没有驱动起不来。我的PC是个3年前的老机器,实在是不想升级系统,于是捣鼓半天捣鼓好了,…...

Stable Diffusion Prompt用法
Stable Diffusion可以根据你输入的提示词(prompt)来绘制出想象中的画面。 1、正向提示词(Prompt): 提高图像质量的prompt: prompt用途HDR, UHD, 64K(HDR、UHD、4K、8K和64K)这样的质量词可以带来巨大的差异提升照片…...

jenkins问题
目录 python 不是内部或外部命令,也不是可运行的程序 ‘cmd’ 不是内部或外部命令,也不是可运行的程序或批处理文件。 git 不是内部或外部命令,也不是可运行的程序或批处理文件。 pywintypes.com_error: (-2147024891, ‘拒绝访问。’, None,…...

阅读笔记DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks
zi,t∈Rz_{i,t}\in \mathbb{R}zi,t∈R表示时间序列iii在ttt时刻的值。给一个连续时间段t∈[1,T]t\in [1, T]t∈[1,T],将其划分为context window[1,t0)[1,t_0)[1,t0)和prediction window[t0,T][t_0,T][t0,T]。用context window的时间序列预测prediction window…...

01.Java的安装
1.JDK&JREJDK : Java SE Development Kit--Java开发工具JRE : Java Runtime Environment--Java运行环境Java编程,需要安装JDK;如果仅仅是运行一款Java程序则只需要运行JREJava的安装包分为两类:一类是JRE--是一个独立的Java运行环境; 一类…...
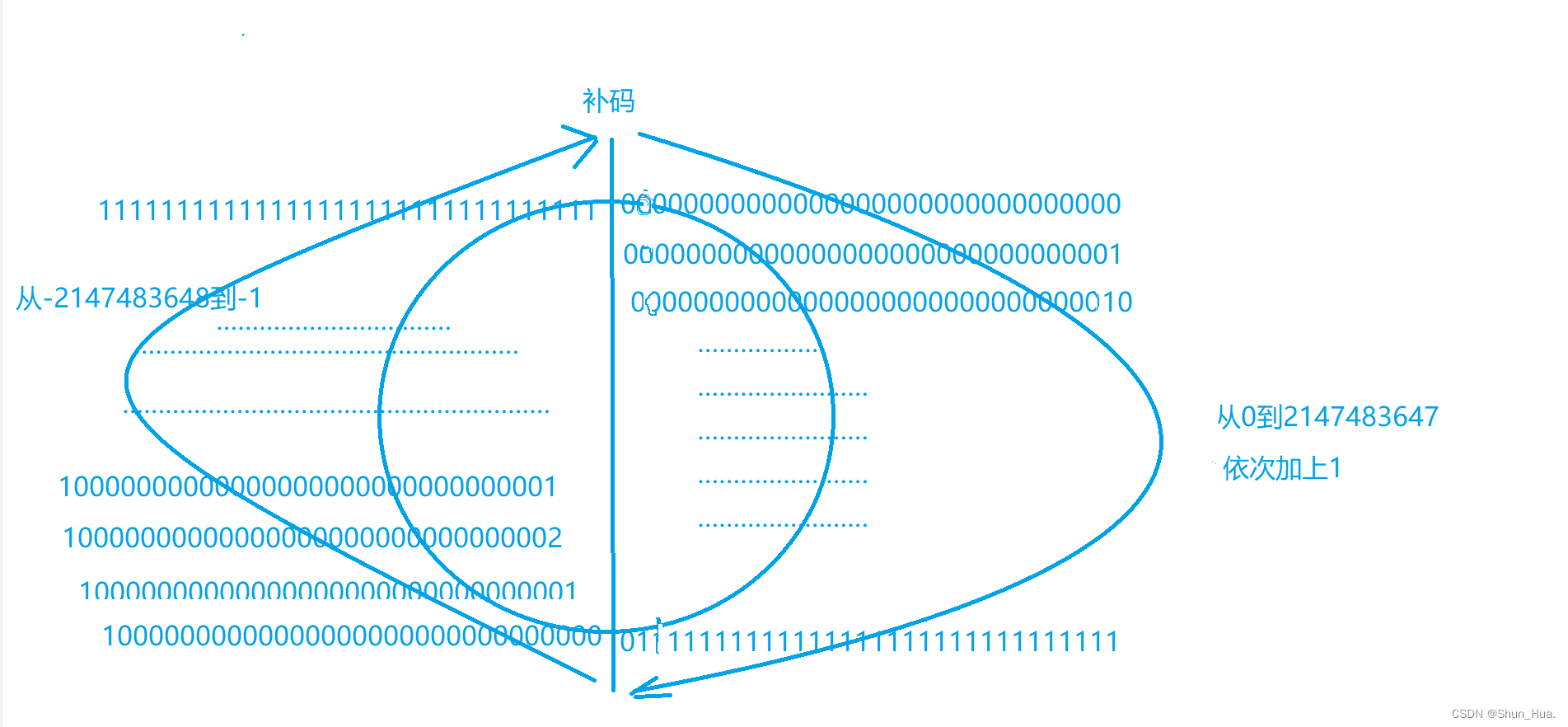
【C语言深度剖析】关键字(全)
文章目录一.存储类型关键字前言补充1:内存思考:补充2:变量与内存的关系补充3:变量的分类补充4:存储类补充5:删除数据是怎么删除的?1.auto2.register3.static4.extern基本用法:基本功能5.typedef…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
