《机器学习》基础概念之【P问题】与【NP问题】
《机器学习》基础概念之【P问题】与【NP问题】
这里写目录标题
- 《机器学习》基础概念之【P问题】与【NP问题】
- 一、多项式&时间复杂度
- 1.1. 多项式
- 1.2.时间复杂度
- 二、P问题 & NP问题
- 2.1. P问题
- 2.2.NP问题
- 2.3.举例理解NP问题-TSP旅行商推销问题
- 三、NP-hard问题&NP-C问题
- 3.1.NP-hard问题
- 3.2. NP-C问题
- 四、P&NP的联系
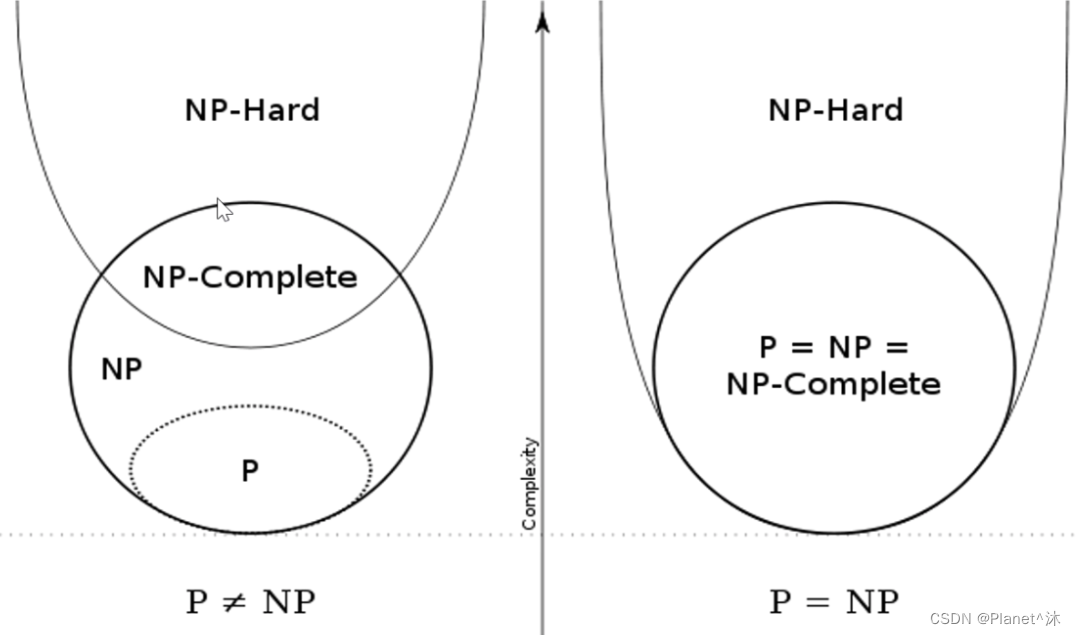
- 4.1. 理想:NP问题 = P问题
- 4.2.现实:我们仍然相信 P问题!=NP问题
一、多项式&时间复杂度
1.1. 多项式
axn+bxn−1+cax^{n} + b x^{n-1}+caxn+bxn−1+c 形如这种形式的就被称为 xxx 的最高位为 nnn 的多项式。
1.2.时间复杂度
定义为:随着问题规模的增大,算法执行时间增长的快慢。
它可以用来表示一个算法运行的 时间效率\red{时间效率}时间效率。
举个例子,冒泡排序的时间复杂度为 O(n2)O(n^2)O(n2) , 取其最高次,可以看出,这是一个时间复杂度为多项式的表示方式。
二、P问题 & NP问题
2.1. P问题
P(deterministic polynomial time question):
多项式时间问题,简称 P 问题,意思是能在多项式时间内解决的问题。
简单理解是算起来很快的问题。
2.2.NP问题
NP(No-deterministic polynomial time question):
非确定多项式时间问题,简称 NP 问题,就是能在多项式时间验证答案正确与否的问题。
简单的理解是NP问题算起来不一定快,但对于任何答案我们都可以快速的验证这个答案对不对。
2.3.举例理解NP问题-TSP旅行商推销问题
最著名的 NP 问题是TSP旅行商推销问题。
题目是在以下条件下,求出访问所有城市的最短路径
- 推销商有N个目的地城市
- 他需要访问所有城市一次,即不能重复
- 任意两座城市都是连接的,距离已知,即对应有权完全图
分析:
解决这个问题如果单纯的用枚举法来列举的话会有(n−1)!(n-1)!(n−1)! 种,已经不是多项式时间的算法了。将会是N的阶乘的复杂度O(n!)O(n!)O(n!)。
但是有快捷的方法,可以用猜的,假设人品爆炸猜几次就猜中了一条小于长度a的路径,TSP问题解决了,皆大欢喜。
可是,我不可能每次都猜的那么准,也许我要猜完所有种方案呢?
所以我们说,这是一个NP类问题。也就是这个问题能在多项式的时间内验证并得出问题的正确解,可是我们却不知道该问题是否存在一个多项式时间的算法,每次都能解决他(注意,这里是不知道,不是不存在,即能解决,但是无法找到一个多项式时间的算法的通解)。
- 其他NP问题:
Edge Cover 边覆盖
Set Cover 集合覆盖
Steiner Tree(Forest) 斯坦纳树
Max cut 最大割
SAT 可满足性
三、NP-hard问题&NP-C问题
3.1.NP-hard问题
- NP-hardness问题:
任意 NP 问题都可以在多项式时间内归约为一类问题,这类问题就称为 NP-hard 问题,这是比所有的NP问题都难的问题。
归约的意思是为了解决问题A,先将问题A归约为另一个问题B,解决问题B同时也间接解决了问题A。
3.2. NP-C问题
- NP-Complete问题:
但若所有的NP问题都能多项式归约到一类问题X,则称X为NP-hard问题,进一步如果X是NP的,称X是NP complete的。
换句话说,只要解决了这个问题,那么所有的NP问题都解决了。其定义要满足2个条件:一是NP-hard的问题,二是NP问题。
四、P&NP的联系
4.1. 理想:NP问题 = P问题
NP=PNP=PNP=P 意思是,如果对于一个问题能在多项式时间内验证其答案的正确性,那么是否能在多项式时间内解决它。
因为如果将所有的NP问题都 多项式规约 到某一个NP Complete问题,且只要一个NP Complete问题能在多项式时间内得到解决的话,那么所有的NP问题都可以在多项式时间内得到解决了。这个问题的解决将会带来世界性的进步。
4.2.现实:我们仍然相信 P问题!=NP问题
P≠NPP {\not=} NPP=NP
至今并没有人能证明某个NP Complete问题是P的。而且目前主流的观点是P不等于NP,当然这也没有确切的证明。如左图所示。
相关文章:

《机器学习》基础概念之【P问题】与【NP问题】
《机器学习》基础概念之【P问题】与【NP问题】 这里写目录标题《机器学习》基础概念之【P问题】与【NP问题】一、多项式&时间复杂度1.1. 多项式1.2.时间复杂度二、P问题 & NP问题2.1. P问题2.2.NP问题2.3.举例理解NP问题-TSP旅行商推销问题三、NP-hard问题&NP-C问题…...

WinRAR安装教程
文章目录WinRAR安装教程无广告1. 下载2. 安装3. 注册4. 去广告WinRAR安装教程无广告 1. 下载 国内官网:https://www.winrar.com.cn/ 2. 安装 双击,使用默认路径: 点击“安装”。 点击“确定”。 点击“完成”。 3. 注册 链接ÿ…...
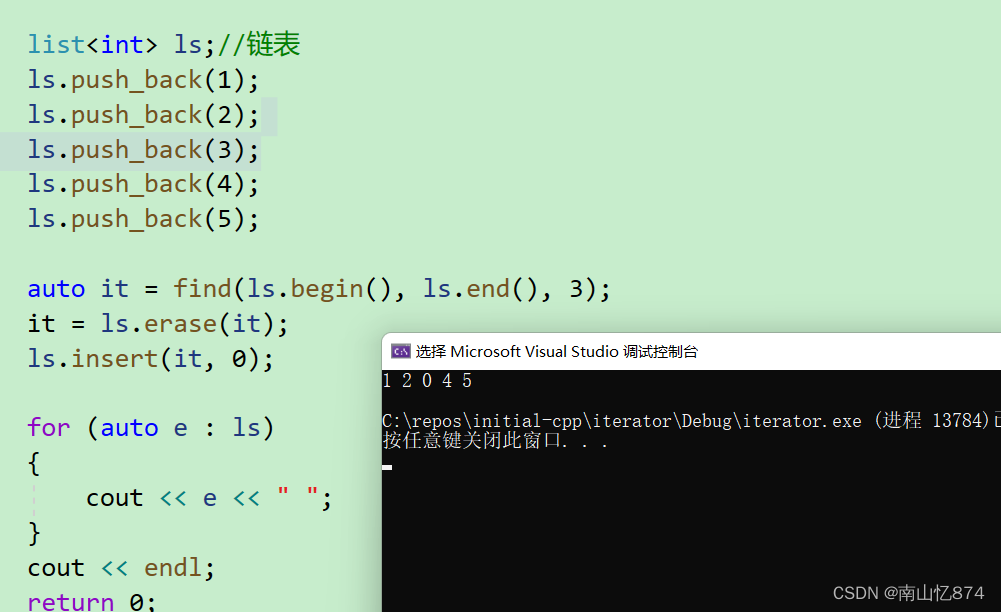
C++:vector和list的迭代器区别和常见迭代器失效问题
迭代器常见问题的汇总vector迭代器和list迭代器的使用vector迭代器list迭代器vector迭代器失效问题list迭代器失效问题vector和list的区别vector迭代器和list迭代器的使用 学习C,使用迭代器和了解迭代器失效的原因是每个初学者都需要掌握的,接下来我们就…...

SpringSecurity如何实现前后端分离
前后端分离模式是指由前端控制页面路由,后端接口也不再返回html数据,而是直接返回业务数据,数据一般是JSON格式。Spring Security默认的表单登录方式,在未登录或登录成功时会发起页面重定向,在提交登录数据时ÿ…...

为ubuntu 18.04添加蓝牙驱动
目录背景方法背景 从网上买的能直接插ubuntu 1804的usb蓝牙太少了,而且还贵。我就直接从JD下单的一个便宜的USB蓝牙,结果插上机器没有驱动起不来。我的PC是个3年前的老机器,实在是不想升级系统,于是捣鼓半天捣鼓好了,…...

Stable Diffusion Prompt用法
Stable Diffusion可以根据你输入的提示词(prompt)来绘制出想象中的画面。 1、正向提示词(Prompt): 提高图像质量的prompt: prompt用途HDR, UHD, 64K(HDR、UHD、4K、8K和64K)这样的质量词可以带来巨大的差异提升照片…...

jenkins问题
目录 python 不是内部或外部命令,也不是可运行的程序 ‘cmd’ 不是内部或外部命令,也不是可运行的程序或批处理文件。 git 不是内部或外部命令,也不是可运行的程序或批处理文件。 pywintypes.com_error: (-2147024891, ‘拒绝访问。’, None,…...

阅读笔记DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks
zi,t∈Rz_{i,t}\in \mathbb{R}zi,t∈R表示时间序列iii在ttt时刻的值。给一个连续时间段t∈[1,T]t\in [1, T]t∈[1,T],将其划分为context window[1,t0)[1,t_0)[1,t0)和prediction window[t0,T][t_0,T][t0,T]。用context window的时间序列预测prediction window…...

01.Java的安装
1.JDK&JREJDK : Java SE Development Kit--Java开发工具JRE : Java Runtime Environment--Java运行环境Java编程,需要安装JDK;如果仅仅是运行一款Java程序则只需要运行JREJava的安装包分为两类:一类是JRE--是一个独立的Java运行环境; 一类…...
【C语言深度剖析】关键字(全)
文章目录一.存储类型关键字前言补充1:内存思考:补充2:变量与内存的关系补充3:变量的分类补充4:存储类补充5:删除数据是怎么删除的?1.auto2.register3.static4.extern基本用法:基本功能5.typedef…...

English Learning - L2 语音作业打卡 双元音 [aʊ] [əʊ] Day15 2023.3.7 周二
English Learning - L2 语音作业打卡 双元音 [aʊ] [əʊ] Day15 2023.3.7 周二💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 /eɪ…...

记第一次面试的过程(C++)
说实话三月份上旬过得很充实,而且感觉蛮值,但还有不足的地方,今晚特地看完资料分析来复盘复盘。 时间还要回到3.2中午13.35(别问我为什么那么准确,刚刚掏手机看的),我正在吃着饭看着王者荣耀的直…...
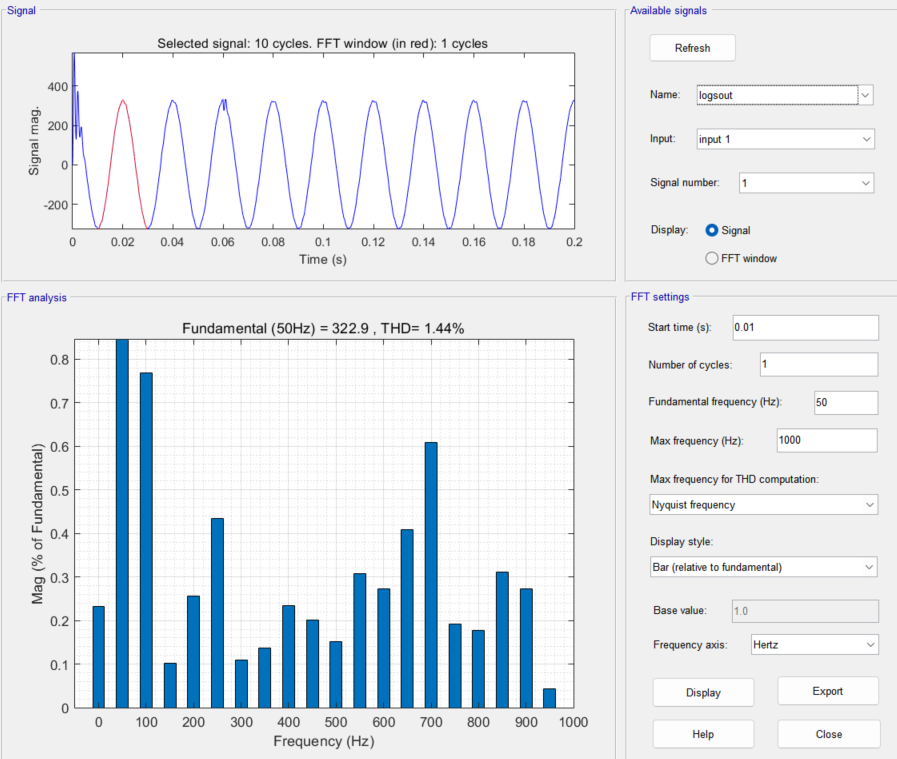
06 电力电子仿真 MATLAB/Simulink
文章目录01 单相半波整流电路02 单相全波整流电路(子系统封装模块)03 三相桥式整流电路(三相模块与示波器使用)04 相控与斩控交交调压(THD计算)05 Buck电路(PWM实现与闭环反馈)06 单…...

搞懂面向对象这五大概念,才算真正跨过初学者到开发者的“分水岭“
文章目录前言一、对象二、类三、面向对象程序设计的特点1. 封装2. 继承3. 多态前言 面向对象程序设计是在面向过程程序设计的基础上发展而来的,它比面向过程编程具有更强的灵活性和扩展性。面向对象程序设计也是一个程序员发展的 “分水岭”,很多的初学者…...

基于DelayQueue实现的延时队列
基于java中延时队列的实现该文章,我们这次主要是来实现基于DelayQueue实现的延时队列。 使用DelayQueue实现的延时队列的步骤: 定义一个继承了Delayed的类,定义其中的属性,并重写compareTo和getDelay两个方法创建一个Delayqueue…...

MATLAB实现层次分析法AHP及案例分析
层次分析法(Analytic Hierarchy Process, AHP) 1 模型背景 美国运筹学家匹兹堡大学教授Saaty在20世纪70年代初提出的一种层次权重决策分析方法。 层次分析法(Analytic Hierarchy Process, AHP)是一种定性和定量分析相结合的决策分析方法。 特点:用较少的定量信息使决策的…...

Vue 3.0 TypeScript支持
Vue CLI 提供内置的 TypeScript 工具支持。 #NPM 包中的官方声明 随着应用的增长,静态类型系统可以帮助防止许多潜在的运行时错误,这就是为什么 Vue 3 是用 TypeScript 编写的。这意味着在 Vue 中使用 TypeScript 不需要任何其他工具——它具有一流的公…...
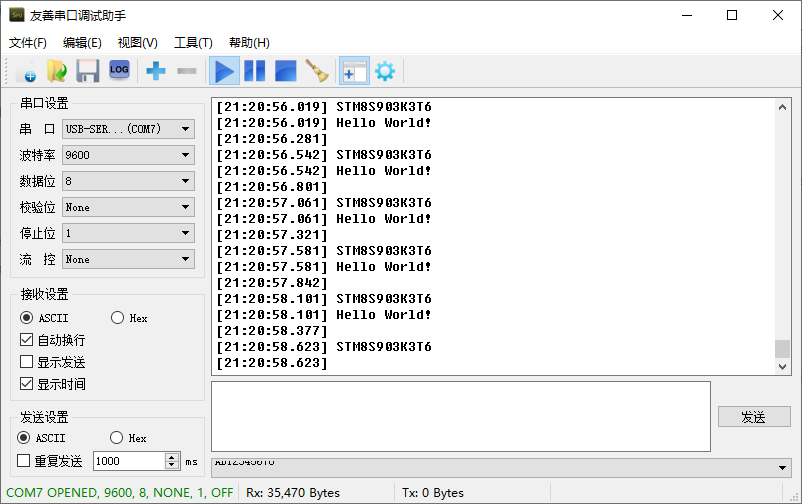
STM8S系列基于IAR标准外设printf输出demo
STM8S系列基于IAR标准外设printf输出demo📌STM8S/A标准外设库(库版本V2.3.1)📍官网标准外设库:https://www.st.com/zh/embedded-software/stsw-stm8069.html ⛳注意事项 🚩在内存空间比较有限的情况下&am…...
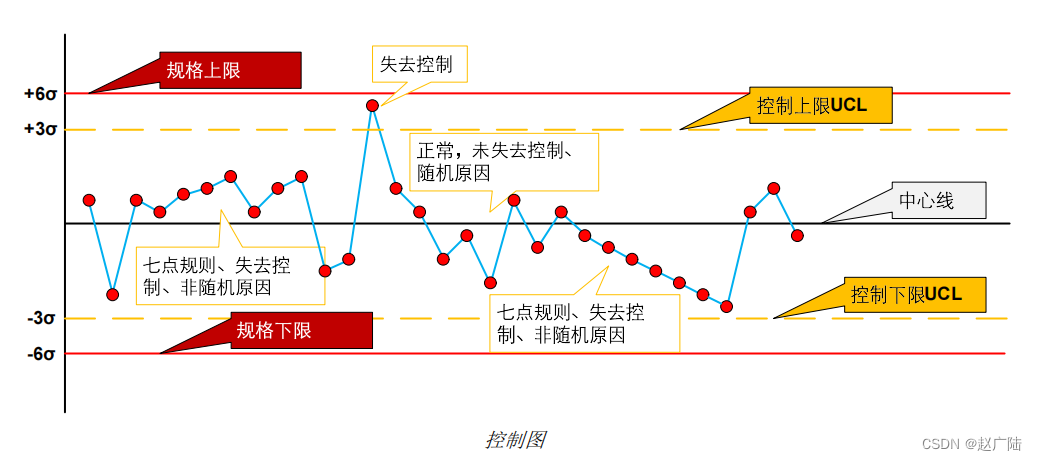
PMP项目管理项目质量管理
目录1 项目质量管理概述2 规划质量管理3 管理质量4 控制质量1 项目质量管理概述 项目质量管理包括把组织的质量政策应用于规则、管理、控制项目和产品质量要求,以满足相关方目标的各个过程。项目质量管理还将以组织的名义支持过程的持续改进活动。 核心概念 质量是…...

前缀和总结
前缀和是一个常用的算法技巧,通常用于求解数组或序列的区间和。 具体来说,假设有一个长度为n的数组a,我们可以预处理出一个长度为n+1的前缀和数组s,其中s[i]表示原数组a前i个元素的和,即: s[i] = a[0] + a[1] + ... + a[i-1] 这样一来,对于任意的区间[l, r],我们可以…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...
