当前位置： 首页 > news >正文

Linux(Ubuntu)下源码开发整个流程完成版本(下载-＞编译-＞模拟器运行)

news 2026/2/8 23:04:50

写这篇文章没别的意思, 年纪大了记性不好, 这次工作中下载,编译遇到了一些之前没遇到的问题,所以就所幸记录一下, 以便日后能快速查阅

好了, 正题开始

首先我们下载AOSP源代码开始

AOSP源代码下载

首先找到官网https://source.android.google.cn/  进入后最上面点击获取源代码

1:如果有梯子, 对着文档一顿操作就行

2:如果没梯子是下不了的, 那么也不是没有办法, 清华镜像站 AOSP | 镜像站使用帮助 | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 

照着一顿操作就可以了, 这两个其实本质上是一样的, 就是repo时候地址换了一下而已

关于源代码下载我有几点需要说明一下:

1:根据上面的操作, 下载的源码仅包含AOSP的部分, 并不包含kernel的和vendor的源码(不知道什么是vendor以及vendor包含什么的自行科普).

2:下载kernel有什么用? 比如我需要看binder的源码, 就少不了可能会涉及到binder驱动, binder.c这个代码是在kernel/common/drivers/android/ 这个位置的(只是举个例子)

3:下载android 源码时在repo init -u url -b android_version  其中的android_version这个位置不是我们通常

相关文章：

Linux(Ubuntu)下源码开发整个流程完成版本(下载-＞编译-＞模拟器运行)

写这篇文章没别的意思, 年纪大了记性不好, 这次工作中下载,编译遇到了一些之前没遇到的问题,所以就所幸记录一下, 以便日后能快速查阅 好了, 正题开始 首先我们下载AOSP源代码开始 AOSP源代码下载 首先找到官网https://source.android.google.cn/ 进入后最上面点击获取源代…...

编程日记 2024/6/29 6:47:05

el-form表单实现校验

前端表单实现&#xff0c; rules 属性传入约定的验证规则&#xff0c;并将 form-Item 的 prop 属性设置为需要验证的特殊键值即可。 <el-form ref"ruleFormRef" :model"interviewForm" label-position"left" require-asterisk-position"…...

编程日记 2024/6/29 6:45:02

一台TrinityCore服务器客户端连接网速慢（未解决）

在FreeBSD开bhyve安装Ubuntu&#xff0c;然后安装了TrinityCore服务器&#xff0c;在只是经过一层NAT&#xff0c;两边都是局域网的情况下&#xff0c;连接速度竟然很慢&#xff0c;慢到600ms。 服务器安装见&#xff1a;尝试在FreeBSD 的jail、bhyve里安装TrinityCore-CSDN博…...

编程日记 2024/6/29 6:44:01

[系统运维|Xshell]宿主机无法连接上NAT网络下的虚拟机进行维护？主机ping不通NAT网络下的虚拟机，虚拟机ping的通主机！解决办法

遇到的问题&#xff1a;主机ping不通NAT网络下的虚拟机&#xff0c;虚拟机ping的通主机 服务器&#xff1a;Linux&#xff08;虚拟机&#xff09; 主机PC&#xff1a;Windows 虚拟机&#xff1a;vb&#xff0c;vm测试过没问题&#xff0c;vnc没测试不清楚 虚拟机网络&#xff1…...

编程日记 2024/6/29 6:41:59

C 语言实例 - 查找数组中最大的元素值

查找数组中最大的元素值。 实例 1 #include <stdio.h>int main() {int array[10] {1, 2, 3, 4, 5, 6, 7, 8, 9, 0};int loop, largest;largest array[0];for(loop 1; loop < 10; loop) {if( largest < array[loop] ) largest array[loop];}printf("最大…...

编程日记 2024/6/29 6:40:57

MySQL之可扩展性(七)

可扩展性 通过集群扩展 理想的扩展方案时单一逻辑数据库能够存储尽可能多的数据&#xff0c;处理尽可能多的查询&#xff0c;并如期望的那样增长。许多人的第一想法就是建立一个"集群"或者"网格"来无缝处理这些事情&#xff0c;这样应用就无须去做太多工…...

编程日记 2024/6/29 6:39:56

微服务框架中Nacos的个人学习心得

微服务框架需要学习的东西很多&#xff0c;基本上我把它分为了五个模块&#xff1a; 第一&#xff1a;微服务技术模块 分为三个常用小模块&#xff1a; 1.微服务治理&#xff1a; 注册发现 远程调用 配置管理 网关路由 2.微服务保护&#xff1a; 流量控制 系统保护 熔断降级 服…...

编程日记 2024/6/29 6:38:53

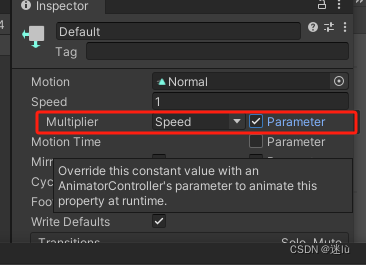
Unity Animator 运行时修改某个动画状态的播放速度

1.添加动画参数&#xff0c;选择需要动态修改速度的动画状态 2.在属性面板种设置速度倍速参数...

编程日记 2024/6/29 6:37:52

阿里云常用的操作

阿里云常见的产品和服务 容器服务 可以查看容器日志、监控容器cpu和内存&#xff0c; 日志服务 SLS 可以查看所有服务的日志&#xff0c; Web应用防火墙 WAF 可以查看 QPS. 阿里云查看集群&#xff1a; 点击 “产品和服务” 中的 容器服务&#xff0c;可以查看 集群列表&…...

编程日记 2024/6/29 6:36:51

【MATLAB源码-第231期】基于matlab的polar码编码译码仿真，对比SC,SCL,BP,SCAN,SSC等译码算法误码率。

操作环境&#xff1a; MATLAB 2022a 1、算法描述 极化码&#xff08;Polar Code&#xff09; 极化码&#xff08;Polar Code&#xff09;是一种新型的信道编码技术&#xff0c;由土耳其裔教授Erdal Arıkan在2008年提出。极化码在理论上被证明能够在信道容量上达到香农极限…...

编程日记 2024/6/29 6:35:50

创新实训(十三) 项目开发——实现用户终止对话功能

思路分析&#xff1a; 如何实现用户终止AI正在进行的回答&#xff1f; 分析实现思路如下&#xff1a; 首先是在用户点击发送后&#xff0c;切换终止对话&#xff0c;点击后大模型终止对话&#xff0c;停止sse&#xff0c;不再接收后端的消息。同时因为对话记录存入数据库是后…...

编程日记 2024/6/29 6:34:49

基于Java+MySQL停车场车位管理系统详细设计和实现(源码+LW+调试文档+讲解等)

&#x1f497;博主介绍&#xff1a;✌全网粉丝10W,CSDN作者、博客专家、全栈领域优质创作者&#xff0c;博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌&#x1f497; &#x1f31f;文末获取源码数据库&#x1f31f; 感兴趣的可以先收藏起来&#xff0c;…...

编程日记 2024/6/29 6:33:48

LeetCode 53.最大子数组和（dp）

给你一个整数数组 nums &#xff0c;请你找出一个具有最大和的连续子数组&#xff08;子数组最少包含一个元素&#xff09;&#xff0c;返回其最大和。 子数组 是数组中的一个连续部分。 示例 1&#xff1a; 输入&#xff1a;nums [-2,1,-3,4,-1,2,1,-5,4] 输出&#xff1a;…...

编程日记 2024/6/29 6:30:44

IOS17闪退问题Assertion failure in void _UIGraphicsBeginImageContextWithOptions

最近项目更新到最新版本IOS17&#xff0c;发现一个以前的页面突然闪退了。原来是IOS17下&#xff0c;这个方法 UIGraphicsBeginImageContext(CGSize size) 已经被移除&#xff0c;原参数如果size为0的话&#xff0c;会出现闪退现象。 根据说明&#xff0c;上述方法已经被替换…...

编程日记 2024/6/29 6:29:42

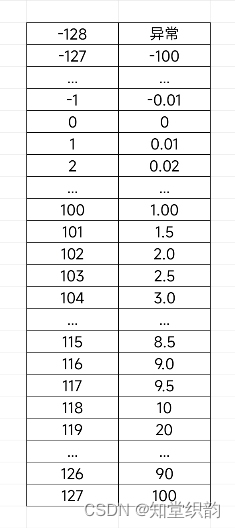
float8格式

产生背景 在人工智能神经元网络中&#xff0c;一个参数用1字节表示即可&#xff0c;或者说&#xff0c;这是个猜想&#xff1a;因为图像的颜色用8比特表示就够了&#xff0c;所以说&#xff0c;猜想神经元的区分度应该小于256。 数字的分配 8比特有256个码位&#xff0c;分为…...

编程日记 2024/6/29 6:27:40

云效BizDevOps上手亲测

云效BizDevOps上手亲测 什么是云效项目协作Projex配置2023业务空间原始诉求字段原始诉求工作流创建原始诉求配置2023产品空间创建主题业务原始诉求关联主题配置2023研发空间新建需求需求关联主题 与传统区别云效开发流程传统开发流程云效BizDevOps 操作体验 什么是云效 在说到…...

编程日记 2024/6/29 6:26:39

亚太杯赛题思路发布（中文版）

导读&#xff1a; 本文将继续修炼回归模型算法&#xff0c;并总结了一些常用的除线性回归模型之外的模型&#xff0c;其中包括一些单模型及集成学习器。 保序回归、多项式回归、多输出回归、多输出K近邻回归、决策树回归、多输出决策树回归、AdaBoost回归、梯度提升决策树回归…...

编程日记 2024/6/29 6:25:38

【Linux】部署 GitLab 服务

1、配置实验环境 安装git apt install git 安装docker apt install docker 安装tree apt install tree 2、安装 Gitlab 下载官方库与安装包 下载官方库的安装脚本 curl https://packages.gitlab.com/install/repositories/gitlab/gitlab-ee/script.deb.sh | sudo bas…...

编程日记 2024/6/29 6:24:37

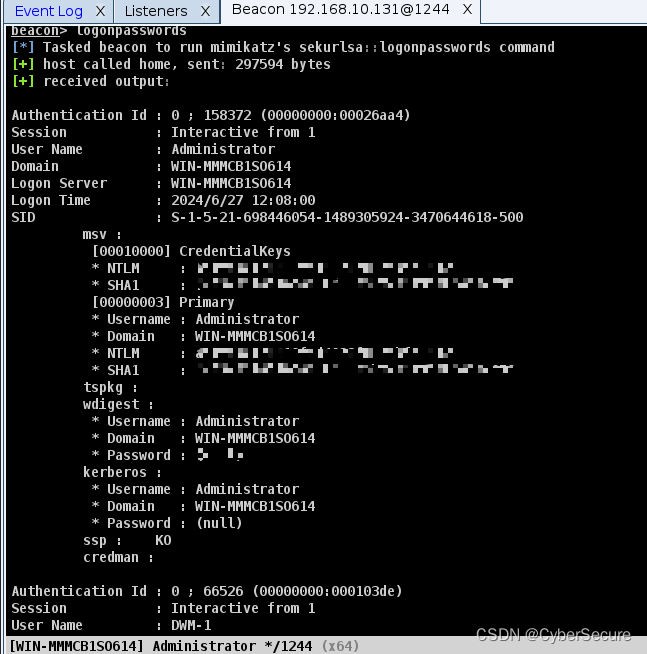
cs与msf权限传递以及mimikatz抓取win2012明文密码

启动服务端 进入客户端 建立监听 制作脚本 客户端运行程序 主机上线 打开msf 调用handler模块 创建监听 11.cs->msf 传递会话 12.传参完成 msf->cs会话传递 抓取密码&#xff08;null&#xff09; 修改注册表 shell reg add "HKEY_LOC…...

编程日记 2024/6/29 6:23:36

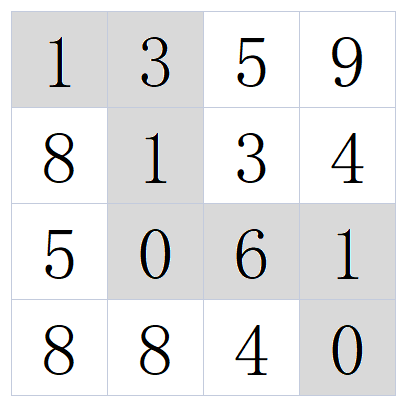
C++ 矩阵的最小路径和解法

描述 给定一个 n * m 的矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。 数据范围: 1≤𝑛,𝑚≤5001≤n,m≤500，矩阵中任意值都满足 0≤𝑎𝑖,𝑗≤1000≤ai,j​≤100 要求…...

编程日记 2024/6/29 6:21:33

UE5 学习系列（二）用户操作界面及介绍

这篇博客是 UE5 学习系列博客的第二篇&#xff0c;在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下&#xff1a; 【Note】&#xff1a;如果你已经完成安装等操作&#xff0c;可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作&#xff0c;重…...

编程新知 2026/2/8 4:37:41

国防科技大学计算机基础课程笔记02信息编码

1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制&#xff0c;因此这个了16进制的数据既可以翻译成为这个机器码&#xff0c;也可以翻译成为这个国标码&#xff0c;所以这个时候很容易会出现这个歧义的情况&#xff1b; 因此&#xff0c;我们的这个国…...

编程新知 2026/2/8 4:37:15

Java 语言特性(面试系列2)

一、SQL 基础 1. 复杂查询 &#xff08;1&#xff09;连接查询&#xff08;JOIN&#xff09; 内连接&#xff08;INNER JOIN&#xff09;&#xff1a;返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

编程新知 2025/10/24 14:20:29

docker详细操作--未完待续

docker介绍 docker官网: Docker&#xff1a;加速容器应用程序开发 harbor官网&#xff1a;Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台&#xff0c;用于将应用程序及其依赖项&#xff08;如库、运行时环…...

编程新知 2026/2/5 4:33:24

Prompt Tuning、P-Tuning、Prefix Tuning的区别

一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning（提示调优） 核心思想：固定预训练模型参数，仅学习额外的连续提示向量（通常是嵌入层的一部分）。实现方式：在输入文本前添加可训练的连续向量（软提示），模型只更新这些提示参数。优势：参数量少（仅提…...

编程新知 2026/2/8 1:14:13

Leetcode 3576. Transform Array to All Equal Elements

Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接&#xff1a;3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到&#xf…...

编程新知 2025/9/17 7:25:07

连锁超市冷库节能解决方案：如何实现超市降本增效

在连锁超市冷库运营中&#xff0c;高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术&#xff0c;实现年省电费15%-60%&#xff0c;且不改动原有装备、安装快捷、…...

编程新知 2025/11/30 16:55:29

【机器视觉】单目测距——运动结构恢复

ps&#xff1a;图是随便找的&#xff0c;为了凑个封面 前言 在前面对光流法进行进一步改进&#xff0c;希望将2D光流推广至3D场景流时&#xff0c;发现2D转3D过程中存在尺度歧义问题&#xff0c;需要补全摄像头拍摄图像中缺失的深度信息&#xff0c;否则解空间不收敛&#xf…...

编程新知 2026/2/8 3:03:01

第25节 Node.js 断言测试

Node.js的assert模块主要用于编写程序的单元测试时使用&#xff0c;通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试&#xff0c;通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

编程新知 2025/10/11 0:24:31

如何为服务器生成TLS证书

TLS&#xff08;Transport Layer Security&#xff09;证书是确保网络通信安全的重要手段&#xff0c;它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书&#xff0c;可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

编程新知 2025/12/17 5:54:30