计算fibonacci数列每一项时所需的递归调用次数
斐波那契数列是一个经典的数列,其中每一项是前两项的和,定义为:
[ F(n) = F(n-1) + F(n-2) ]
其中,( F(0) = 0 ) 和 ( F(1) = 1 )。
对于计算斐波那契数列的第 ( n ) 项,如果使用简单的递归方法,其时间复杂度是指数级的,因为每次递归调用都会产生两个新的调用,直到达到基本情况 ( F(0) ) 或 ( F(1) )。这意味着对于第 ( n ) 项,递归调用的次数大约是 ( 2^n )。
然而,这种简单的递归方法非常低效,因为它会重复计算很多项。一个更高效的方法是使用动态规划(DP)或者记忆化搜索(Memoization),这样可以将时间复杂度降低到 ( O(n) ),并且递归调用的次数也会相应减少。
如果我们考虑一个更高效的算法,例如使用动态规划,那么递归调用的次数将不再是指数级的,而是线性的,即最多 ( n ) 次。这是因为每个状态(即每个斐波那契数)只计算一次,并且存储结果以供后续使用。
相关文章:

计算fibonacci数列每一项时所需的递归调用次数
斐波那契数列是一个经典的数列,其中每一项是前两项的和,定义为: [ F(n) F(n-1) F(n-2) ] 其中,( F(0) 0 ) 和 ( F(1) 1 )。 对于计算斐波那契数列的第 ( n ) 项,如果使用简单的递归方法,其时间复杂度是…...

【教学类65-05】20240627秘密花园涂色书(中四班练习)
【教学类65-03】20240622秘密花园涂色书03(通义万相)(A4横版1张,一大 68张纸136份)-CSDN博客 背景需求: 打印以下几款秘密花园样式(每款10份)给中四班孩子玩一下,看看效果 【教学类…...
)
Python 学习之基础语法(一)
Python的语法基础主要包括以下几个方面,下面将逐一进行分点表示和归纳: 一、基本语法 1. 注释 a. 单行注释:使用#开头,例如# 这是一个单行注释。 b. 多行注释:使用三引号(可以是三个单引号或三个双引号&…...
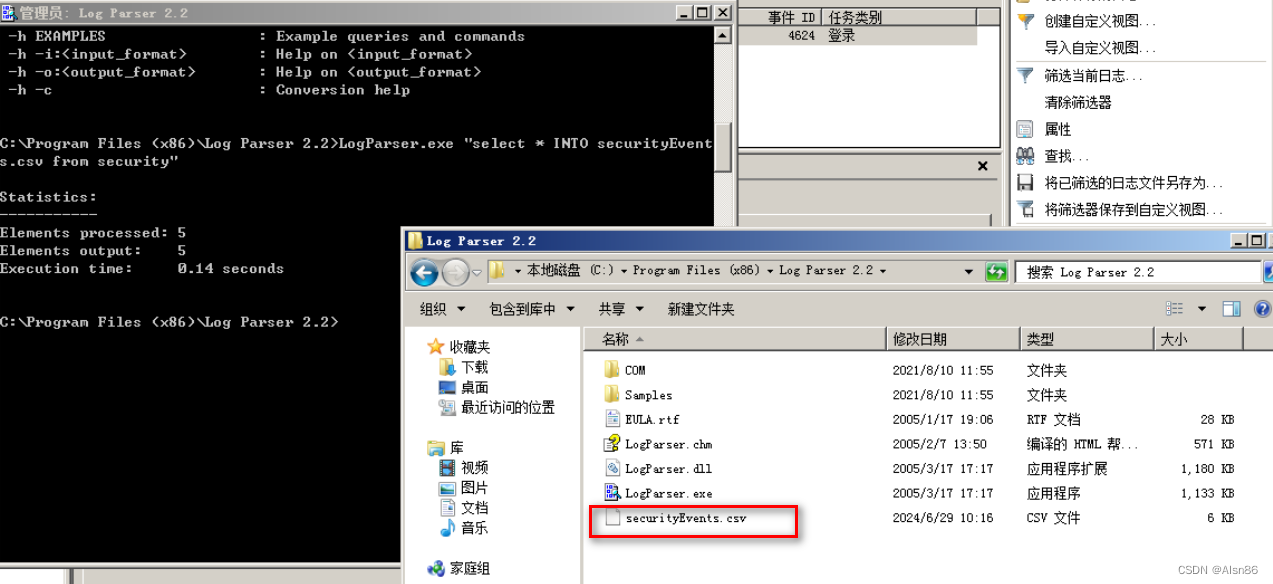
日志分析-windows系统日志分析
日志分析-windows系统日志分析 使用事件查看器分析Windows系统日志 cmd命令 eventvwr 筛选 清除日志、注销并重新登陆,查看日志情况 Windows7和Windowserver2008R2的主机日志保存在C:\Windows\System32\winevt\Logs文件夹下,Security.evtx即为W…...

【ARM】MDK工程切换高版本的编译器后出现error A1137E报错
【更多软件使用问题请点击亿道电子官方网站】 1、 文档目标 解决工程从Compiler 5切换到Compiler 6进行编译时出现一些非语法问题上的报错。 2、 问题场景 对于一些使用Compiler 5进行编译的工程,要切换到Compiler 6进行编译的时候,原本无任何报错警告…...

深入 SSH:解锁本地转发、远程转发和动态转发的潜力
文章目录 前言一、解锁内部服务:SSH 本地转发1.1 什么是 SSH 本地转发1.2 本地转发应用场景 二、打开外部访问大门:SSH 远程转发2.1 什么是 SSH 远程转发2.2 远程转发应用场景 三、动态转发:SSH 让你拥有自己的 VPN3.1 什么是 SSH 动态转发3.…...

python如何把一个函数的返回值,当成这个函数的参数值
python如何把一个函数的返回值,当成这个函数的参数值 1. 递归调用 递归是一种函数自己调用自己的方法。在递归调用中,你可以将前一次调用的返回值作为下一次调用的参数。 def recursive_function(x):# 函数逻辑if 条件满足:return 结果else:return rec…...

【融合ChatGPT等AI模型】Python-GEE遥感云大数据分析、管理与可视化及多领域案例应用
随着航空、航天、近地空间遥感平台的持续发展,遥感技术近年来取得显著进步。遥感数据的空间、时间、光谱分辨率及数据量均大幅提升,呈现出大数据特征。这为相关研究带来了新机遇,但同时也带来巨大挑战。传统的工作站和服务器已无法满足大区域…...
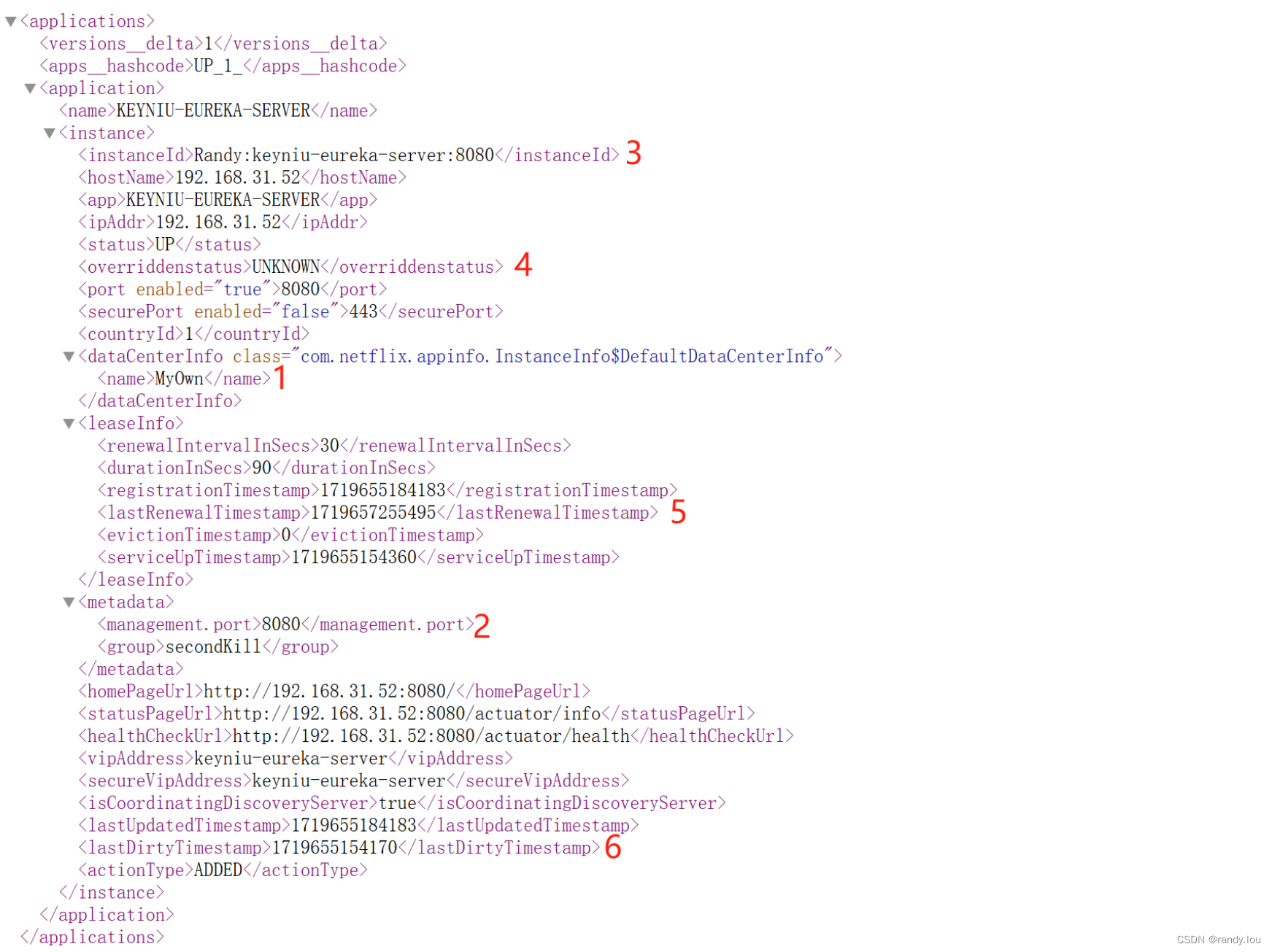
SpringBoot: Eureka入门
1. IP列表 公司发展到一定的规模之后,应用拆分是无可避免的。假设我们有2个服务(服务A、服务B),如果服务A要调用服务B,我们能怎么做呢?最简单的方法是让服务A配置服务B的所有节点的IP,在服务A内部做负载均衡调用服务B…...

Typescript 【实用教程】(2024最新版)含类型声明,类型断言,函数,接口,泛型等
简介 TypeScript 是 JavaScript 的超集,是 JavaScript(弱类型语言) 的强类型版本。 拥有类型机制文件后缀 .tsTypescript type ES6TypeScript 和 JavaScript 的关系类似 less 和 css 的关系TypeScript对 JavaScript 添加了一些扩展&#x…...
智慧校园-实训管理系统总体概述
智慧校园实训管理系统,专为满足高等教育与职业教育的特定需求而设计,它代表了实训课程管理领域的一次数字化飞跃。此系统旨在通过革新实训的组织结构、执行流程及评估标准,来增强学生的实践操作技能和教师的授课效率,为社会输送具…...

如何用GPT开发一个基于 GPT 的应用?
原文发自博客:GPT应用开发小记 如何开发一个基于 GPT 的应用?答案就在问题里,那就是用 GPT 来开发基于 GPT 的应用。本文以笔者的一个开源项目 myGPTReader 为例,分享我是如何基于 GPT 去开发这个系统的,这个系统的功能…...
)
大数据生态体系中各组件的区别面试题(更新)
一、MapReduce与Spark有什么区别? 1、处理方式: MapReduce基于磁盘处理数据,将中间结果保存到磁盘中,减少了内存占用,计算速度慢。 基于内存处理数据,将计算的中间结果保存到内存中,计算速度快。2、资源申请方式&…...

数字信号处理实验一(离散信号及离散系统的MATLAB编程实现)
实验要求: 离散信号及离散系统的MATLAB编程实现(2学时) 要求: 编写一程序,输出一定长度(点数),具有一定幅度、(角)频率和初始相位的实(或复&…...

数字图像处理专栏——introduction
Introduction: 数字图像处理技术是我在深入学习研究的方向之一。本科期间跟随导师做基于AndroidOpenCV的病虫识别app,因此入门,我也对该部分知识有进一步探索的欲望,但更多的是因该脚踏实地一步步记录,一步步成长。 本篇从数字图…...

Django 模版继承
1,设计母版页 Test/templates/6/base.html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><!-- 修正了模板标签的全角字符问题 -->{% block title %}<title>这个是母版页</title>{…...
)
Apipost接口测试工具的原理及应用详解(一)
本系列文章简介: 随着软件行业的快速发展,API(应用程序编程接口)作为不同软件组件之间通信的桥梁,其重要性日益凸显。API的质量直接关系到软件系统的稳定性、性能和用户体验。因此,对API进行严格的测试成为…...
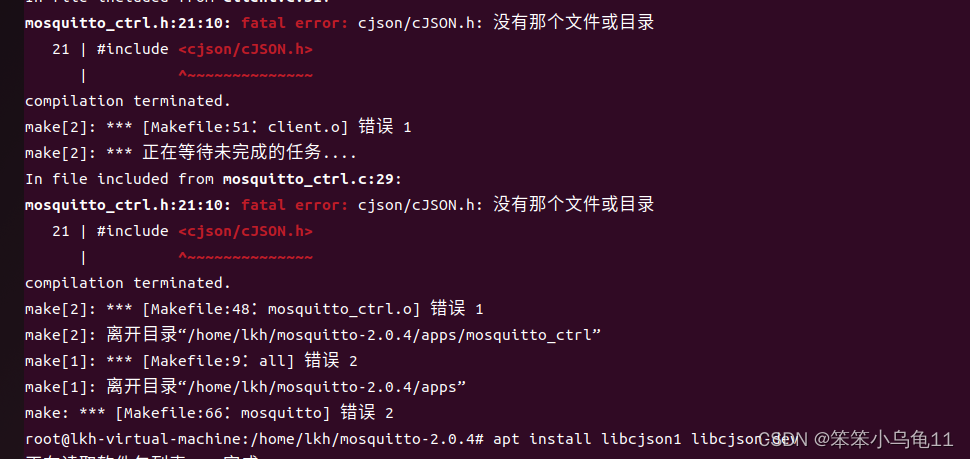
一款轻量级的通信协议---MQTT (内含Linux环境搭建)
目录 MQTT MQTT的关键特点: 应用场景 Linux环境搭建: 1. 安装mosquitto 2. Linux下客户端进行通信 3. PC端和Linux下进行通信 安装MQTT. fx 4. MQTT.fx的使用 1. 点击连接 编辑 2. 连接成功 3. 订阅主题或者给别的主题发送消息 遇到的问…...

记netty本地客户端断线无法自动重连 or 远程客户端自动重连本地服务端
记netty客户端断线无法自动完成重连 or 服务端无法让客户端断线重连 引场景案例bootstrap 引 netty既能开发socket服务端,也可开发客户端,实现连接的全双工通信。在客户端断线重启后,可自动重连服务端。 场景 本地代码既有socket客户端也有…...

UNIAPP_在js文件中使用i18n国际化
导入 import { initVueI18n } from dcloudio/uni-i18n import messages from /locale/index const { t } initVueI18n(messages) 使用 t(config.request.i001)....
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...
