弱监督实例分割 Box-supervised Instance Segmentation with Level Set Evolution 论文笔记
弱监督实例分割 Box-supervised Instance Segmentation with Level Set Evolution 论文笔记
- 一、Abstract
- 二、引言
- 三、相关工作
- 3.1 基于 Box 的实例分割
- 3.2 基于层级的分割
- 四、提出的方法
- 4.1 图像分割中的层级模型
- 4.2 基于 Box 的实例分割
- 在 Bounding Box 内的层级进化
- 输入的数据格式
- 层级初始化
- 4.3 训练和推理
- 损失函数
- 推理
- 五、实验
- 5.1 数据集
- 5.2 实施细节
- 5.3 主要结果
- 5.4 消融实验
- 层级能量
- 高层特征的通道数量
- 训练计划
- 深度结构特征的有效性
- 六、结论
写在前面
这是一篇基于 Box 的弱监督实例分割文章,之前也分享过几篇(主页有,欢迎关注一下呗~),采用旧纸堆里面翻出来的能量函数来做弱监督。
- 论文地址:Box-supervised Instance Segmentation with Level Set Evolution
- 代码地址:https://github.com/LiWentomng/boxlevelset
- 收录于:ECCV 2022
- 补一下博客篇数,2023年每周一篇,还剩下6篇未补。欢迎关注,长年稳定更新~
一、Abstract
本文提出一种 single-shot 的基于 box 监督的实例分割方法,致力于整合传统的能量函数模型以及深度神经网络。具体来说,以一种端到端的方式,通过一个连续的 Chan-Vese 能量函数来迭代地学习一系列层级(mask?):采用 SLOLv2 来自适应地预测实例感知的 mask 作为每一个实例层级。所有的输入图像及提取的特征都用来进化层级曲线,其中一个 box 投影函数用来获得初始的边界。通过最小化可微分的能量函数,每个实例的层级在其对应的 box 标注框内被迭代地优化,实验结果很牛皮。
二、引言
第一段实例分割的目的,应用,之前方法对于标注的依赖。
第二段介绍现有的基于 Box 的方法,基于伪标签的以及颜色相似度的,即 BBTP 和 Boxinst。本文指出这两种方法过于简化了一个假设:像素或者颜色对被强制共享相同的颜色,于是来自相似形状目标和背景的噪声上下文无可避免地会影响训练,使得性能不太好。
本文提出一种 single-shot 的基于 box 监督的实例分割方法来解决这些问题,致力于整合传统的能量集合模型以及深度神经网络。以一种端到端的方式在标注的 Bounding box 内,从隐藏的曲线卷积中来迭代地学习一系列层级(mask?)。
具体来说,引入一种传统 Chan-Vese 能量函数,并采用 SOLOv2来预测实例感知的mask 图来作为每个实例的层级。除输入的特征图外,还采用了一种长范围依赖的深度结构特征来稳定地进化层级曲线,得以向目标边界逼近。通过最小化可微分的能量函数,每个实例的层级在其对应的 box 标注框内被迭代地优化,实验结果很牛皮。
贡献如下:
- 第一个提出一种基于层级进化的方法用在基于 box 的弱监督实例分割上;
- 将深度结构特征并入低层级的图像,在 bounding box 区域内实现稳定的层级进化,其中一个 box 的投影函数用于层级初始化。
- 在 COCO、PASCAL VOC、遥感数据集 iSAID 和医疗数据集 LiTS上效果很好。
三、相关工作
3.1 基于 Box 的实例分割
讲一下最近的方法,指出 BBTP 和 Boxinst,这两种方法过于简化了一个假设:像素或者颜色对被强制共享相同的颜色,因此来自相似形状目标和背景的噪声上下文无可避免地会影响训练,使得性能不太好。除了这两个外,最近的 BBAM 和 DIscoBox 关注于代理 mask 标签的生成,需要多个阶段的训练或者多个网络结构。而本文提出的基于层级方法以一种端到端的隐含方式通过优化 box 区域内的能量函数来迭代地对齐实例边界。
3.2 基于层级的分割
主要划分为两类:基于区域和边缘的方法。核心理念是在一个高维度通过一个能量函数来展现隐藏的曲线,而这能够用梯度下降来优化。接下来是一些举例,指出他们的不足:全监督方式训练网络去预测不同的子区域并得到目标的边界,而本文提出的是 box 级别的监督。
四、提出的方法
一些符号:输入的图像 IimgI_{img}Iimg,高层深度特征 IfeatI_{feat}Ifeat,初始层级 ϕ0\phi_0ϕ0

4.1 图像分割中的层级模型
对层级方法的回顾:将图像分割视为一种连续的能量最小化问题。
Mumford-Shah 层级模型:给定一图像 III,找到一组参数化的轮廓 CCC,将图像层级 Ω∈R2\Omega\in\mathbb{R}^2Ω∈R2 划分为 NNN 个不联通的区域 Ω1,⋯,ΩN\Omega_1, \cdots, \Omega_NΩ1,⋯,ΩN。Mumford-Shah 能量函数 FMS\mathcal F^{MS}FMS 定义如下:
FMS(u1,⋯,uN,Ω1,⋯,ΩN)=∑i=1N(∫Ωi(I−ui)2dxdy+μ∫Ωi∣∇ui∣2dxdy+γ∣Ci∣),\mathcal F^{MS}(u_1,\cdots,u_N,\Omega_1,\cdots,\Omega_N)=\sum\limits_{i=1}^{N}(\int\limits_{\Omega_i}(I-u_i)^2dxdy+\mu\int\limits_{\Omega_i}|\nabla u_i|^2dxdy+\gamma|C_i|), FMS(u1,⋯,uN,Ω1,⋯,ΩN)=i=1∑N(Ωi∫(I−ui)2dxdy+μΩi∫∣∇ui∣2dxdy+γ∣Ci∣),其中 uiu_iui 为接近于输入 III 的光滑分段函数,目的是确保每个区域 Ωi\Omega_iΩi 内的光滑。μ\muμ,γ\gammaγ 为加权系数。
之后 Chan 和 Vese 简化了这一能量函数:
FCV(ϕ,x,c2)=∫Q∣I(x,y)−c1∣2H(ϕ(x,y))dxdy+∫Q∣I(x,y)−c2∣2(1−H(ϕ(x,y)))dxdy+γ∫Q∣∇H(ϕ(x,y))∣dxdy\begin{aligned}\mathcal{F}^{\text{CV}}(\phi,x,c_2)&=\int\limits_{Q}\left|I(x,y)-c_1\right|^2H(\phi(x,y))dxdy\\ &+\int\limits_{Q}\left|I(x,y)-c_2\right|^2(1-H(\phi(x,y)))dxdy+\gamma\int\limits_{Q}\left|\nabla H(\phi(x,y))\right|dxdy\end{aligned} FCV(ϕ,x,c2)=Q∫∣I(x,y)−c1∣2H(ϕ(x,y))dxdy+Q∫∣I(x,y)−c2∣2(1−H(ϕ(x,y)))dxdy+γQ∫∣∇H(ϕ(x,y))∣dxdy其中 HHH 为 Heaviside 海塞函数,ϕ(x,y)\phi(x,y)ϕ(x,y) 为层级函数,如果为 0 则表示轮廓 C={(x,y):ϕ(x,y)=0}C=\{(x,y):\phi(x,y)=0\}C={(x,y):ϕ(x,y)=0} 将图像空间 Ω\OmegaΩ 划为两个不连通区域,内部轮廓为 C:Ω1={(x,y):ϕ(x,y)>0}C\colon\Omega_1=\{(x,y):\phi(x,y)>0\}C:Ω1={(x,y):ϕ(x,y)>0},外部轮廓为 C:Ω2={(x,y):ϕ(x,y)<0}C\colon\Omega_2=\{(x,y):\phi(x,y)<0\}C:Ω2={(x,y):ϕ(x,y)<0}。上式右边一二项倾向于拟合数据,第三项用一个非负系数 γ\gammaγ 归一化 000 层级轮廓。c1c_1c1,c2c_2c2 分别为 CCC 内部和 CCC 外部的输入 I(x,y)I(x,y)I(x,y) 的均值。
于是通过 c1c_1c1 和 c2c_2c2 找到一个层级函数 ϕ(x,y)=0\phi(x,y)=0ϕ(x,y)=0 来优化能量函数 FCV\mathcal{F}^{\text{CV}}FCV,从而得到图像的分割结果。
4.2 基于 Box 的实例分割
在 Bounding Box 内的层级进化
给定输入图像 I(x,y)I(x,y)I(x,y),旨在标注的 bounding box B\mathcal{B}B 区域内隐式地进化出一组层级来预测目标边界曲线。由 SOLOv2 预测出的尺寸为 H×WH\times WH×W 的 mask M∈RH×W×S2M\in\mathbb{R}^{H\times W\times S^2}M∈RH×W×S2 包含 S×SS\times SS×S 个可能的实例图。每一个可能的实例图仅包含一个实例,他们的中心位于 (i,j)(i,j)(i,j)。位置 (i,j)(i,j)(i,j) 处预测出 mask 类别概率 pi,j∗>0p^{*}_{i,j}>0pi,j∗>0 时被视为正样本。然后将 box B\mathcal{B}B 内的每个正样本图作为层级 ϕ(x,y)\phi(x,y)ϕ(x,y),其输入图像 I(x,y)I(x,y)I(x,y) 相应的像素空间被视为 Ω\OmegaΩ,即 Ω∈B\Omega\in\mathcal{B}Ω∈B。当 C={(x,y):ϕ(x,y)=0}C=\{(x,y):\phi(x,y)=0\}C={(x,y):ϕ(x,y)=0} 时,对应的 CCC 为分割出的边界,此时 box 区域被划分为不相连的前景和背景区域。
通过优化下面的能量函数来学习一系列的层级 ϕ(x,y)\phi(x,y)ϕ(x,y):
F(ϕ,I,c1,c2,B)=∫Ω∈B∣I∗(x,y)−c1∣2σ(ϕ(x,y))dxdy+∫Ω∈B∣I∗(x,y)−c2∣2(1−σ(ϕ(x,y)))dxdy+γ∫Ω∈B∣∇σ(ϕ(x,y))∣dxdy\begin{aligned} \mathcal{F}\left(\phi, I, c_{1}, c_{2}, \mathcal{B}\right) & =\int_{\Omega \in \mathcal{B}}\left|I^{*}(x, y)-c_{1}\right|^{2} \sigma(\phi(x, y)) d x d y \\ & +\int_{\Omega \in \mathcal{B}}\left|I^{*}(x, y)-c_{2}\right|^{2}(1-\sigma(\phi(x, y))) d x d y+\gamma \int_{\Omega \in \mathcal{B}}|\nabla \sigma(\phi(x, y))| d x d y \end{aligned} F(ϕ,I,c1,c2,B)=∫Ω∈B∣I∗(x,y)−c1∣2σ(ϕ(x,y))dxdy+∫Ω∈B∣I∗(x,y)−c2∣2(1−σ(ϕ(x,y)))dxdy+γ∫Ω∈B∣∇σ(ϕ(x,y))∣dxdy其中 I∗(x,y)I^{*}(x,y)I∗(x,y) 表示归一化后的图像 I(x,y)I(x,y)I(x,y),γ\gammaγ 为非负系数,σ\sigmaσ 为 sigmoidsigmoidsigmoid 函数,其被视为层级 ϕ(x,y)\phi(x, y)ϕ(x,y) 的特征函数。相比于传统的 Heaviside 海塞函数,sigmoidsigmoidsigmoid 更为光滑,能够更好地表示预测实例的特征以及提高层级进化在训练过程中的收敛。上式右边一二项旨在强制预测的 ϕ(x,y)\phi(x, y)ϕ(x,y) 统一内部区域 Ω\OmegaΩ 和外部区域 Ωˉ\bar\OmegaΩˉ。c1c_1c1,c2c_2c2 为 Ω\OmegaΩ 和 Ωˉ\bar\OmegaΩˉ 的均值,定义如下:
c1(ϕ)=∫Ω∈BI∗(x,y)σ(ϕ(x,y))dxdy∫Ω∈Bσ(ϕ(x,y))dxdy,c2(ϕ)=∫Ω∈BI∗(x,y)(1−σ(ϕ(x,y)))dxdy∫Ω∈B(1−σ(ϕ(x,y)))dxdyc_1(\phi)=\dfrac{\int\limits_{\Omega\in\mathbb{B}}I^*(x,y)\sigma(\phi(x,y))dxdy}{\int\limits_{\Omega\in\mathbb{B}}\sigma(\phi(x,y))dxdy},~~c_2(\phi)=\dfrac{\int\limits_{\Omega\in\mathcal{B}}I^*(x,y)(1-\sigma(\phi(x,y)))dxdy}{\int\limits_{\Omega\in\mathcal{B}}(1-\sigma(\phi(x,y)))dxdy} c1(ϕ)=Ω∈B∫σ(ϕ(x,y))dxdyΩ∈B∫I∗(x,y)σ(ϕ(x,y))dxdy, c2(ϕ)=Ω∈B∫(1−σ(ϕ(x,y)))dxdyΩ∈B∫I∗(x,y)(1−σ(ϕ(x,y)))dxdy能量函数 F\mathcal{F}F 可以在训练过程中利用梯度反向传播来优化。当时间步 t≥0t\ge0t≥0 时,能量函数 F\mathcal{F}F 对 ϕ\phiϕ 的微分可表示为:
∂ϕ∂t=−∂F∂ϕ=−∇σ(ϕ)[(I∗(x,y)−c1)2−(I∗(x,y)−c2)2+γdiv(∇ϕ∣∇ϕ∣)]\dfrac{\partial\phi}{\partial t}=-\dfrac{\partial F}{\partial\phi}=-\nabla\sigma(\phi)[(I^*(x,y)-c_1)^2-(I^*(x,y)-c_2)^2+\gamma div\left(\dfrac{\nabla\phi}{|\nabla\phi|}\right)] ∂t∂ϕ=−∂ϕ∂F=−∇σ(ϕ)[(I∗(x,y)−c1)2−(I∗(x,y)−c2)2+γdiv(∣∇ϕ∣∇ϕ)]其中 ∇\nabla∇ 和 divdivdiv 分别为空间求导以及散度算子。于是 ϕ\phiϕ 的更新为:
ϕi=ϕi−1+Δt∂ϕi−1∂t\phi_i=\phi_{i-1}+\Delta t\dfrac{\partial\phi_{i-1}}{\partial t} ϕi=ϕi−1+Δt∂t∂ϕi−1上式可以视为沿着能量函数下降方向的一个隐式的曲线进化,而最优的实例边界 CCC 可以借助迭代拟合 ϕi−1\phi_{i-1}ϕi−1,从而最小化能量函数 F\mathcal{F}F 获得:
infΩ∈B{F(ϕ)}≈0≈F(ϕi)\operatorname*{inf}_{\Omega\in\mathcal{B}}\{\mathcal{F}(\phi)\}\approx0\approx\mathcal{F}(\phi_i) Ω∈Binf{F(ϕ)}≈0≈F(ϕi)
输入的数据格式
除输入低水平的图像特征 IuI_uIu 外,还采用嵌入了图像语言信息的高层深度特征 IfI_fIf 来获得更加鲁棒的结果。将 SOLOv2 中所有 FPN 层的 mask 特征 FmaskF_{\text mask}Fmask 送入到一个卷积层来提取高层特征 IfI_fIf。此外,还通过树滤波器来增强 IfI_fIf,这利用了最小跨越树(minimal spanning tree?)来建模长距离依赖并保存目标结构。为层级进化构建的整体能量函数为:
F(ϕ)=λ1∗F(ϕ,Iu,cu1,cu2,B)+λ2∗F(ϕ,If,cf1,cf2,B),\mathcal F(\phi)=\lambda_1*\mathcal F(\phi,I_u,c_{u_1},c_{u_2},\mathcal B)+\lambda_2*\mathcal F(\phi,I_f,c_{f_1},c_{f_2},\mathcal B),\quad\text{} F(ϕ)=λ1∗F(ϕ,Iu,cu1,cu2,B)+λ2∗F(ϕ,If,cf1,cf2,B),其中 λ1\lambda_1λ1 和 λ2\lambda_2λ2 分别为平衡两种特征的权重,cu1c_{u_1}cu1、cu2c_{u_2}cu2、cf1c_{f_1}cf1、cf2c_{f_2}cf2 分别为输入 IuI_uIu 和 IfI_fIf 的均值。
层级初始化
利用 box 投影函数来促进模型自动地生成一个粗糙估计的初始层级 ϕ0\phi_0ϕ0。
通过赋值 GT box 上的每个位置来得到二值化的区域 mb∈{0,1}H×Wm^b\in\{0,1\}^{H\times W}mb∈{0,1}H×W。每一个实例预测的 mask 得分 mp∈{0,1}H×Wm^p\in\{0,1\}^{H\times W}mp∈{0,1}H×W 被视为前景概率。box 投影函数 F(ϕ0)box\mathcal{F}(\phi_0)_{box}F(ϕ0)box 定义如下:
F(ϕ0)box=Pdice(mxp,mxb)+Pdice(myp,myb)\mathcal{F}(\phi_0)_{box}=\mathcal{P}_{dice}(m_x^p,m_x^b)+\mathcal{P}_{dice}(m_y^p,m_y^b) F(ϕ0)box=Pdice(mxp,mxb)+Pdice(myp,myb)其中 mxpm_x^pmxp、mxbm_x^bmxb、mypm_y^pmyp、mybm_y^bmyb 分别为 xxx 和 yyy 坐标轴上mask 预测值 mpm^pmp 和二值化 GT 区域 mbm^bmb 的投影,Pdice\mathcal{P}_{dice}Pdice 表示这一投影操作具有 1-D dice 系数加权。
4.3 训练和推理
损失函数
损失函数 LLL 包含两部分,分类损失 LcateL_{cate}Lcate 和 box 监督下的实例分割损失 LinstL_{inst}Linst:L=Lcate+LinstL= L_{cate}+L_{inst}L=Lcate+Linst,其中 LcateL_{cate}Lcate 为 Focal 损失,LinstL_{inst}Linst 为可微分的层级能量函数:
Linst=1Npos∑k1{pi,j∗>0}{F(ϕ)+αF(ϕ0)box}L_{inst}=\dfrac{1}{N_{pos}}\sum_k\mathbb{1}_{\{p_{i,j}^{*}>0\}}\{\mathcal{F}(\phi)+\alpha\mathcal{F}(\phi_0)_{box}\} Linst=Npos1k∑1{pi,j∗>0}{F(ϕ)+αF(ϕ0)box}其中 NposN_{pos}Npos 表示正样本的索引,pi,j∗{p_{i,j}^{*}}pi,j∗ 为目标位置 (i,j)(i,j)(i,j) 上的类别概率。1\mathbb{1}1 为索引函数,这能确保仅有正的实例 mask 样本才能执行层级进化,如果 pi,j∗>0p_{i,j}^{*}>0pi,j∗>0,1\mathbb{1}1 为 1,反之为 0。α\alphaα 为权重系数,实验设置为 0.3.
推理
推理过程和 SOLOv2 一致:输入图像,利用 NMS 产生有效的 mask。仅有一点不同:采用了额外的一个卷积层来生成高层特征。
五、实验
5.1 数据集
Pascal VOC、COCO、iSAID、LiTS。
5.2 实施细节
AdamW 优化器,8 块 V100(还是够壕~),12 或 36 个 epochs。ResNet + ImageNet 预训练权重作为 Backbone。COCO 数据集:学习率 10−410^{-4}10−4,batch 16。Pascal VOC 数据集:初始学习率 5×10−55\times10^{-5}5×10−5,batch 8,在这两个数据集上,尺度随机缩放 640-800。iSAID 和 LiTS 有着相同的设置,COCO AP 作为评估指标,非负权重 γ\gammaγ 设为 10−410^{-4}10−4。
5.3 主要结果



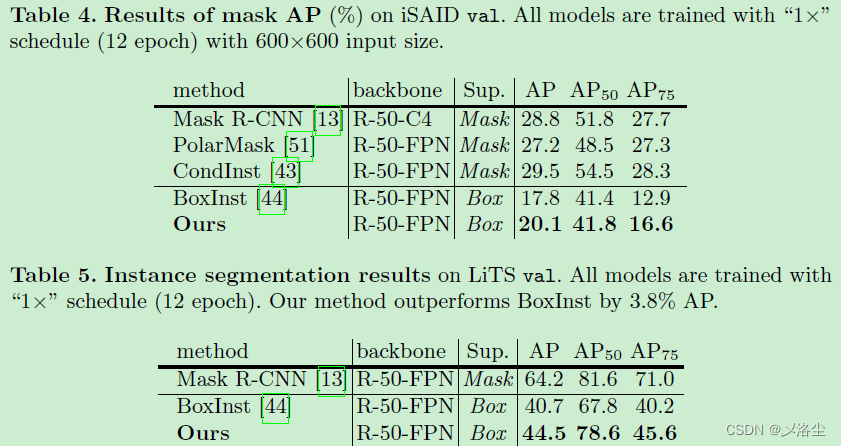



5.4 消融实验
消融实验在 Pascal VOC 数据集上进行:
层级能量

高层特征的通道数量
表 7。
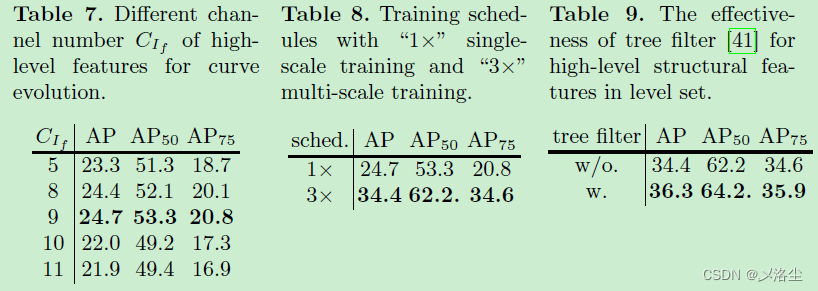
训练计划
表 8。
深度结构特征的有效性
表 9。
六、结论
本文提出了一种 single-shot 的基于 box 的弱监督实例分割方法,能够以端到端的方式迭代地学习一系列层级函数:一种实例感知 mask 图用于预测和作为层级,输入的图像和提取的深度特征用于进化层级曲线,其中一个投影损失函数用于获得初始的边界。通过最小化可微分的能量函数,每个实例的层级能够在相应的 bounding box 标注内迭代地优化,大量的实验表明方法很牛。
写在后面
本文结合若干年前的能量函数方法与现有的深度学习方法进行弱监督实例分割,属实是一锄头挖进往日的纸质期刊堆了,不排除有越来越多的方法~
相关文章:

弱监督实例分割 Box-supervised Instance Segmentation with Level Set Evolution 论文笔记
弱监督实例分割 Box-supervised Instance Segmentation with Level Set Evolution 论文笔记一、Abstract二、引言三、相关工作3.1 基于 Box 的实例分割3.2 基于层级的分割四、提出的方法4.1 图像分割中的层级模型4.2 基于 Box 的实例分割在 Bounding Box 内的层级进化输入的数据…...
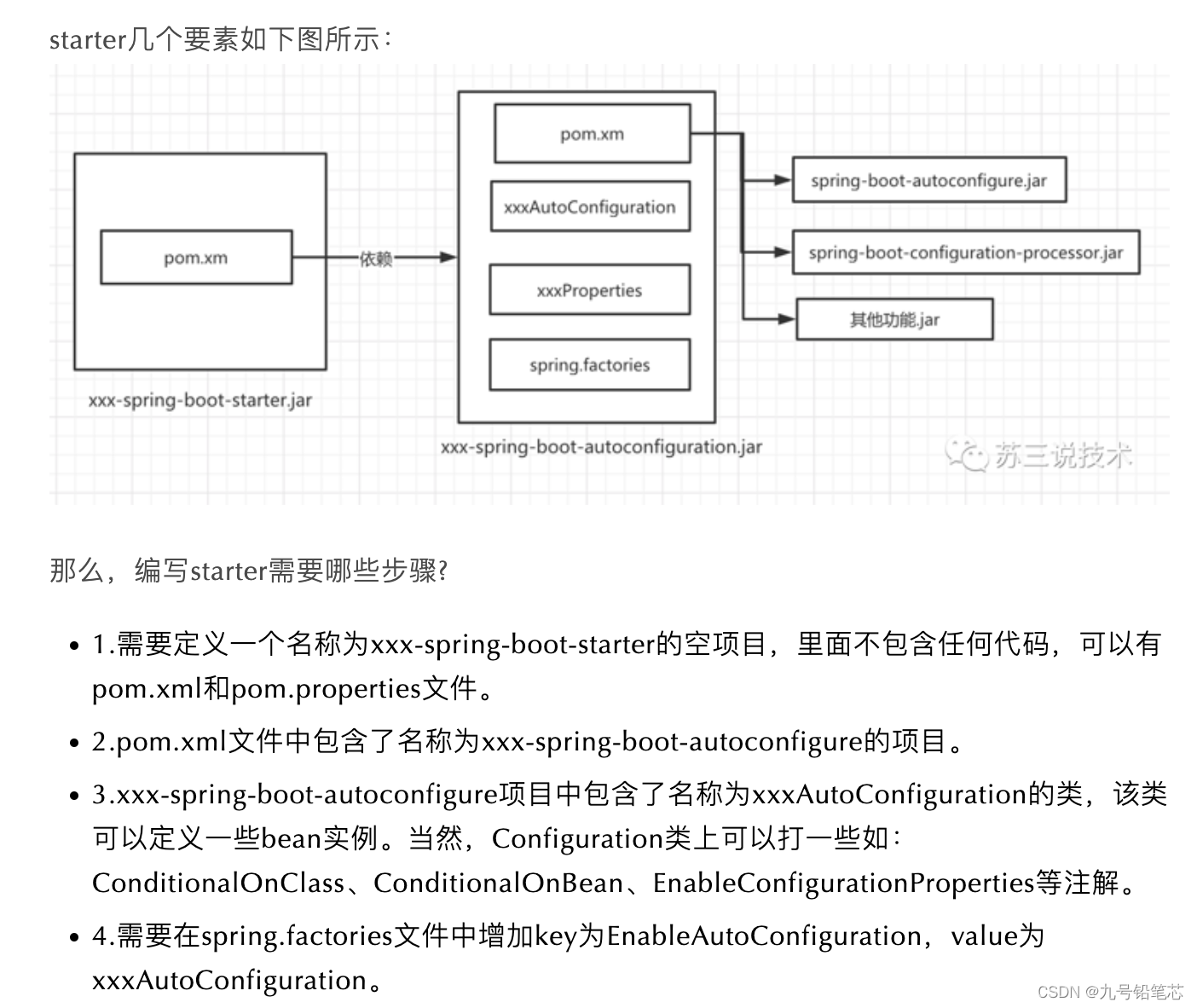
Springboot是什么
目录 为什么会要用springboot 1、之前 2、现在 springboot优点 springboot四大核心 自动装配介绍 1、自动装配作用是什么 2、自动装配原理 springboot starter是什么 1、starter作用 2、比如:我们想搭建java web框架 3、starter原理 SpringBootApplica…...
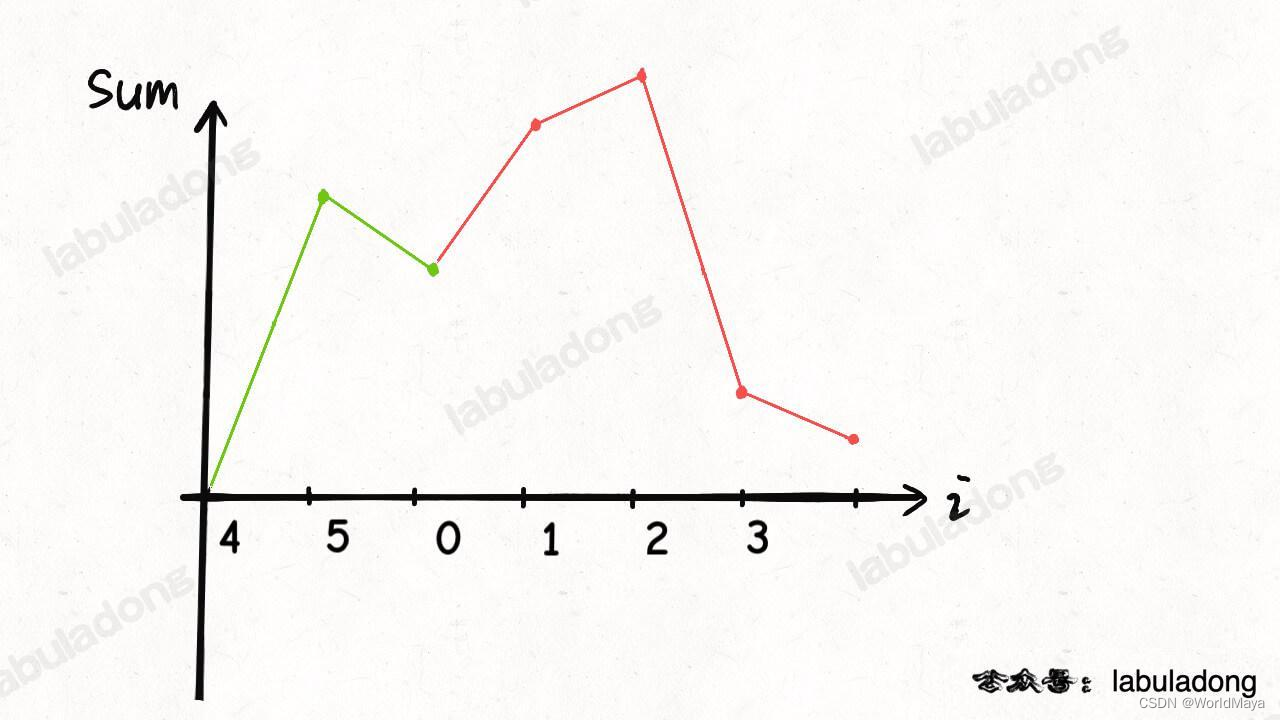
LeetCode 134. 加油站(函数图像法 / 贪心)
题目: 链接:LeetCode 134. 加油站 难度:中等 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[i] 升。你从其中…...

王道计算机组成原理课代表 - 考研计算机 第三章 存储系统 究极精华总结笔记
本篇博客是考研期间学习王道课程 传送门 的笔记,以及一整年里对 计算机组成 知识点的理解的总结。希望对新一届的计算机考研人提供帮助!!! 关于对 存储系统 章节知识点总结的十分全面,涵括了《计算机组成原理》课程里…...
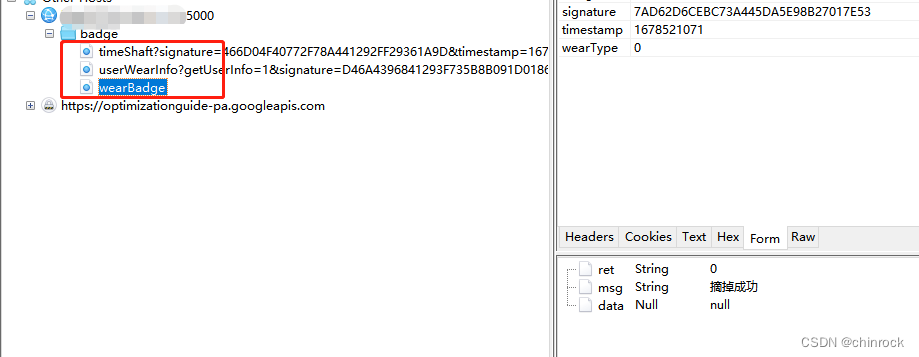
Flask-mock接口数据流程
背景:由于在开发过程中,会遇到以下的痛点 1.服务端接口提测延期,具体接口逻辑未完成实现,接口未能正常调通,导致客户端提测停滞; 2.因为前期已在技术评审上已与客户端开发定好接口字段,客户端比…...

springboot项目配置序列化,反序列化器
介绍本文介绍在项目中时间类型、枚举类型的序列化和反序列化自定义的处理类,也可以使用注解。建议枚举都实现一个统一的接口,方便处理。我这定义了一个Dict接口。枚举类型注解处理这种方式比较灵活,可以让枚举按照自己的方式序列化࿰…...
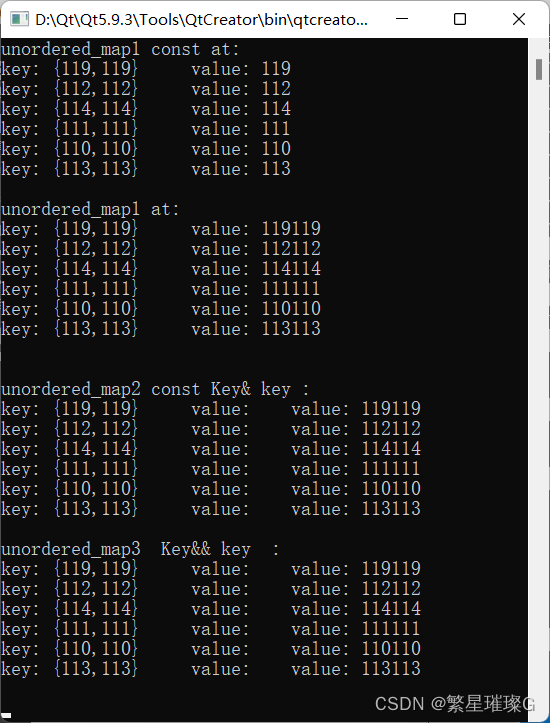
c++11 标准模板(STL)(std::unordered_map)(九)
定义于头文件 <unordered_map> template< class Key, class T, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator< std::pair<const Key, T> > > class unordered…...

Seay代码审计工具
一、简介Seay是基于C#语言开发的一款针对PHP代码安全性审计的系统,主要运行于Windows系统上。这款软件能够发现SQL注入、代码执行、命令执行、文件包含、文件上传、绕过转义防护、拒绝服务、XSS跨站、信息泄露、任意URL跳转等漏洞,基本上覆盖常见PHP漏洞…...
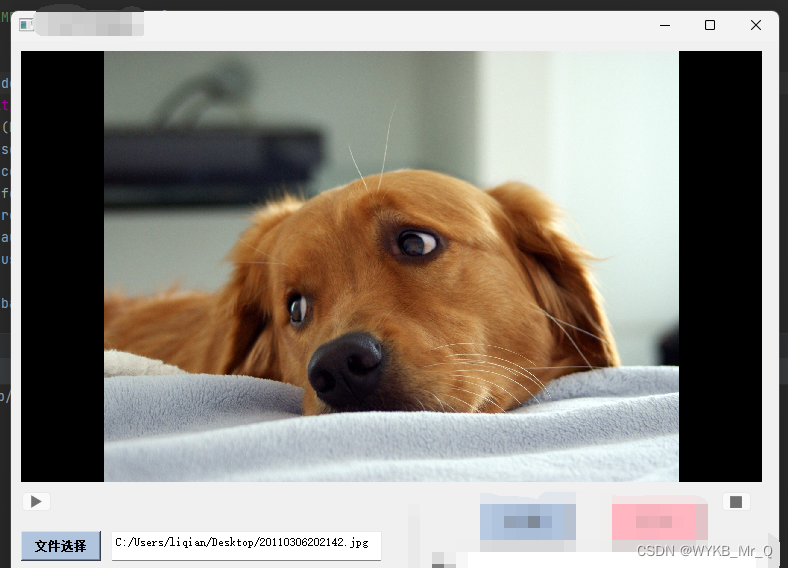
界面开发(4)--- PyQt5实现打开图像及视频播放功能
PyQt5创建打开图像及播放视频页面 上篇文章主要介绍了如何实现登录界面的账号密码注册及登录功能,还简单介绍了有关数据库的连接方法。这篇文章我们介绍一下如何在设计的页面中打开本地的图像,以及实现视频播放功能。 实现打开图像功能 为了便于记录实…...
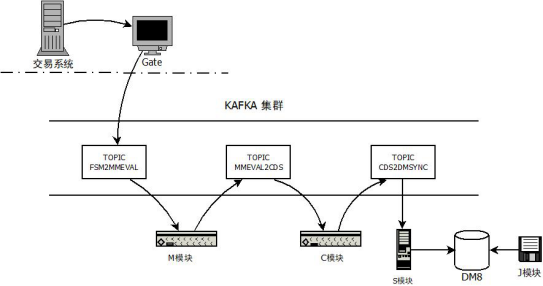
核心系统国产平台迁移验证
核心系统国产平台迁移验证 摘要:信息技术应用创新,旨在实现信息技术领域的自主可控,保障国家信息安全。金融领域又是关系国家经济命脉的行业,而对核心交易系统的信息技术应用创新是交易所未来将要面临的重大挑战。为了推进国产化进…...

【数据结构之二叉树】——二叉树的概念及结构,特殊的二叉树和二叉树性质
文章目录一、二叉树的概念及结构1.概念2.现实中的二叉树3. 特殊的二叉树:3.二叉树的性质二、二叉树练习题总结一、二叉树的概念及结构 1.概念 一棵二叉树是结点的一个有限集合,该集合: 或者为空由一个根节点加上两棵别称为左子树和右子树的二叉树组成…...

Android学习之帧动画和视图动画
帧动画 帧动画中的每一帧其实都是一张图片,将许多图片连起来播放,就形成了帧动画。 在drawable目录下新建frmae_animation文件,在这个文件中定义了帧动画的每一帧要显示的图片,播放时,按从上到下显示。 <?xml v…...

vue2和vue3的区别
这周呢主要就是整理整理学的东西,不然看的也记不住,把这些学的东西做成笔记,感觉会清楚许多,这次就把vue2和vue3的区别总结一下,明天要考四级,嗐,本来想着复习四级,结果只写了一两套…...
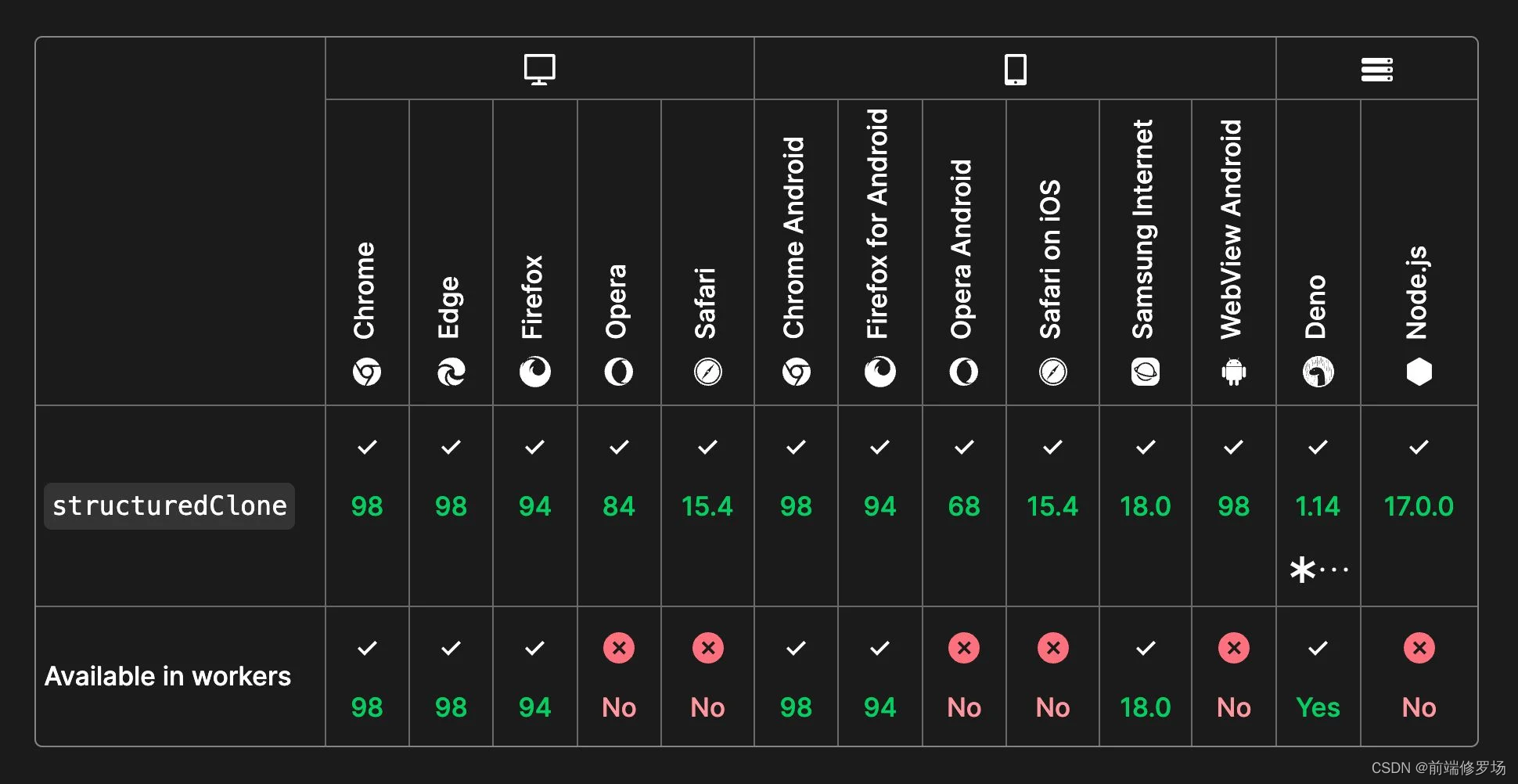
【你不知道的事】JavaScript 中用一种更先进的方式进行深拷贝:structuredClone
你是否知道,JavaScript中有一种原生的方法来做对象的深拷贝? 本文我们要介绍的是 structuredClone 函数,它是内置在 JavaScript 运行时中的: const calendarEvent {title: "Builder.io Conf",date: new Date(123),attendees: ["Steve…...
XE开发Linux应用(二)-Webservice
新建一个工程。选择如图。继续输入服务名然后就生成对应的单元。增加linux 平台。完善对应的单元代码{ Invokable implementation File for Txaliontest which implements Ixaliontest }unit xaliontestImpl;interfaceuses Soap.InvokeRegistry, System.Types, Soap.XSBuiltIns…...

kubernetes实战与源码学习
1.1 关于Kubernetes的介绍与核心对象概念 关于Kubernetes的介绍与核心对象概念-阿里云开发者社区 k8s架构 核心对象 使用kubeadm10分钟部署k8集群 使用 KuboardSpray 安装kubernetes_v1.23.1 | Kuboard k8s-上部署第一个应用程序 Deployment基本概念 给应用添加service&a…...

CNCF x Alibaba云原生技术公开课 第八章 应用配置管理
Pod配置管理分类 可变配置就用 ConfigMap;敏感信息是用 Secret;身份认证是用 ServiceAccount;资源配置是用 Resources;安全管控是用 SecurityContext;前置校验是用 InitContainers。 1、ConfigMap 概念:…...

YUV实践记录
文章目录YUV基础介绍:不同采样YUV格式的区别为什么要使用YUV格式呢?YUV的存储方式Android中的YUV_420_888附录:YUV基础介绍: YUV在做手机图像或者视频处理的时候会经常用到的一个格式,用此文来记录YUV相关介绍…...

【题解】百度2020校招Web前端工程师笔试卷(第一批):单选题、多选题
题目来源 若有错误请指正! 单选 1 分页存储管理将进程的逻辑地址空间分成若干个页,并为各页加以编号,从0开始,若某一计算机主存按字节编址,逻辑地址和物理地址都是32位,页表项大小为4字节,若…...
)
探索云原生技术之容器编排引擎-kubeadm安装kubernetes1.21.10(新版:针对高版本内核)
❤️作者简介:2022新星计划第三季云原生与云计算赛道Top5🏅、华为云享专家🏅、云原生领域潜力新星🏅 💛博客首页:C站个人主页🌞 💗作者目的:如有错误请指正,将…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...
