Leetcode - 133双周赛
目录
一,3190. 使所有元素都可以被 3 整除的最少操作数
二,3191. 使二进制数组全部等于 1 的最少操作次数 I
三,3192. 使二进制数组全部等于 1 的最少操作次数 II
四,3193. 统计逆序对的数目
一,3190. 使所有元素都可以被 3 整除的最少操作数

本题可以直接模拟,如果使用减法操作,那么需要操作 x % 3 次;如果使用加法操作,那么需要操作 3 - x % 3 次。问最少的操作次数,直接取两者的最小值就行。
代码如下:
class Solution {public int minimumOperations(int[] nums) {int ans = 0;for(int x : nums){ans += Math.min(Math.abs(3-x%3), x%3);}return ans;}
}二,3191. 使二进制数组全部等于 1 的最少操作次数 I

本题直接从左往右遍历,注 i < nums.length-2 :
- 遇到0,将nums[i],nums[i+1],nums[i+2] 反转(即 ^1),ans++
- 遇到1,什么都不做
- 循环结束判断后两个数是否全为1,如果是,返回ans;否则返回-1
代码如下:
class Solution {public int minOperations(int[] nums) {int ans = 0;int i = 0;for(; i<nums.length-2; i++){if(nums[i]==0){nums[i] ^= 1;nums[i+1] ^= 1;nums[i+2] ^= 1;ans++;}}return nums[i]==1 && nums[i+1]==1 ? ans : -1;}
}三,3192. 使二进制数组全部等于 1 的最少操作次数 II

本题也可以采用上述做法,代码如下:
class Solution {public int minOperations(int[] nums) {int n = nums.length;int ans = 0;for(int i=0; i<n; i++){if(nums[i] == 0){for(int j=i; j<n; j++)nums[j] ^= 1;ans++;}}return ans;}
}但是该做法是O(n^2)的时间复杂度,会超时,那么上述做法还有哪里可以优化?可以发现如果一个数执行 ^1操作偶数次,它就会变回原来的值,所以我们可以统计后续元素需要执行反转操作的次数cnt,在枚举到x时,如果cnt为奇数,x ^=1,再判断 x 是否为 0,如果为0,cnt++。依次类推,最终得到的cnt就是答案。
代码如下:
class Solution {public int minOperations(int[] nums) {int ans = 0;for(int i=0; i<nums.length; i++){if(ans%2==1)nums[i] ^= 1;if(nums[i] == 0){ans++;}}return ans;}
}四,3193. 统计逆序对的数目

本题可以从后先前考虑,假设有3个数,构造逆序对为2的排序:
- 如果最后一个数是2,那么该数与[0,i-1]能组成0个逆序对,就需要[0,i-1]有2个逆序对
- 如果最后一个数是1,那么该数与[0,i-1]能组成1个逆序对,就需要[0,i-1]有1个逆序对
- 如果最后一个数是0,那么该数与[0,i-1]能组成2个逆序对,就需要[0,i-1]有0个逆序对
依次类推,上述问题就化成了与原问题相同的子问题。可以定义dfs(i,j):前 i 个数有 j 个逆序对时的排序个数。
- 没有requirements束缚,假设 k 为 perm[i] 小于[0,i-1]元素的个数,即 perm[i] 能产生 k 个逆序对,那么问题就转换成了前 i-1个数有 j - k 个逆序对的排序个数。(注:k <= Math.min(i,j))
- 有requirements束缚,该问题就只能转换成前 i-1个数有 req[i-1] 个逆序对的排序个数。(注:req[i-1] <= j && req[i-1] >= j - i,这两个条件就表示req[i-1]的范围必须在[ j - i,j],可以这样理解,当前perm[i]能与前i-1个数组成[0,i]个逆序对,那么前i-1个数需要有[j - i,j]个逆序对)
代码如下:
class Solution {public int numberOfPermutations(int n, int[][] requirements) {int[] req = new int[n];Arrays.fill(req, -1);req[0] = 0;for(int[] x : requirements){req[x[0]] = x[1];}if(req[0]>0) return 0; for(int[] r : memo)Arrays.fill(r, -1);return dfs(n-1, req[n-1], req);}int[][] memo = new int[301][401];int dfs(int i, int j, int[] req){if(i == 0) return 1;if(memo[i][j] != -1) return memo[i][j];int res = 0;int cnt = req[i-1];if(cnt >= 0){if(cnt <= j && cnt >= j-i)res = dfs(i-1, cnt, req);}else{for(int k=0; k<=Math.min(i, j); k++){res = (res + dfs(i-1, j-k, req))%1_000_000_007;}}return memo[i][j] = res;}
}相关文章:

Leetcode - 133双周赛
目录 一,3190. 使所有元素都可以被 3 整除的最少操作数 二,3191. 使二进制数组全部等于 1 的最少操作次数 I 三,3192. 使二进制数组全部等于 1 的最少操作次数 II 四,3193. 统计逆序对的数目 一,3190. 使所有元素都…...
C++总结
...
汽车免拆诊断案例 | 2016 款吉利帝豪EV车无法加速
故障现象 一辆2016款吉利帝豪EV车,累计行驶里程约为28.4万km,车主反映车辆无法加速。 故障诊断 接车后路试,行驶约1 km,踩下加速踏板,无法加速,车速为20 km/h左右,同时组合仪表上的电机及控制…...

前端开发之webpack
安装与入门超详细!webpack入门教程(一)-腾讯云开发者社区-腾讯云...

将内容复制到剪贴板?分享 1 段优质 JS 代码片段!
大家好,我是大澈! 本文约 600 字,整篇阅读约需 1 分钟。 每日分享一段优质代码片段。 今天分享一段 JS 代码片段,使用 Clipboard API 实现将内容复制到剪贴板。 老规矩,先阅读代码片段并思考,再看代码解析…...
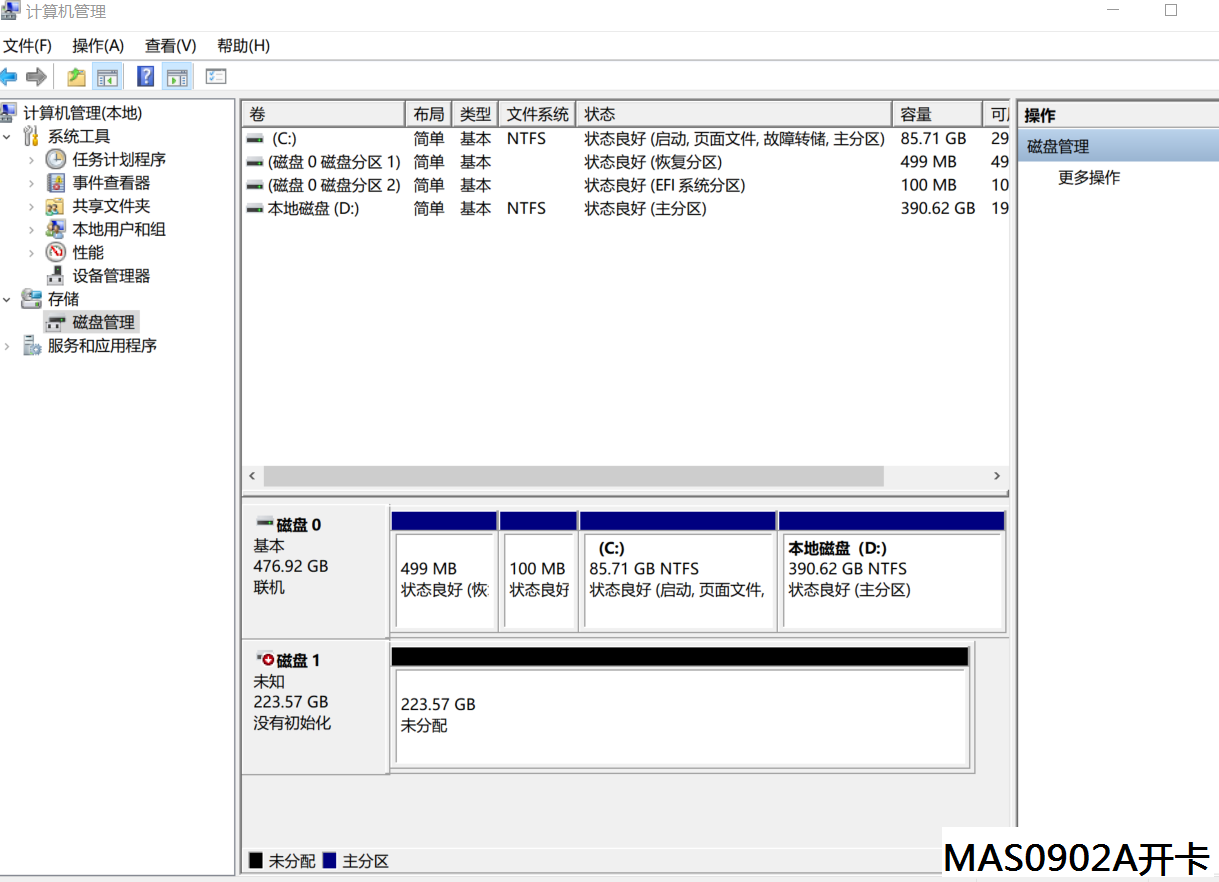
MAS0902量产工具分享,MAS0902A开卡教程,MAS0901量产工具下载
MAS0902和MAS1102都是基于SATA3.2技术开发的DRAM-less SSD控制芯片,简单来说就是SATA协议无缓存主控。下面是我摸索的麦光黑金300 240G SSD开卡修复简易教程,也就是MAS0902量产过程: 注意:开卡转接线必须要用ASM1153E或JMS578主控…...
从我邮毕业啦!!!
引言 时间过的好快,转眼间就要从北邮毕业了,距离上一次月度总结又过去了两个月,故作本次总结。 PS: https://github.com/WeiXiao-Hyy/blog整理了后端开发的知识网络,欢迎Star! 毕业🎓 6月1号完成了自己的…...
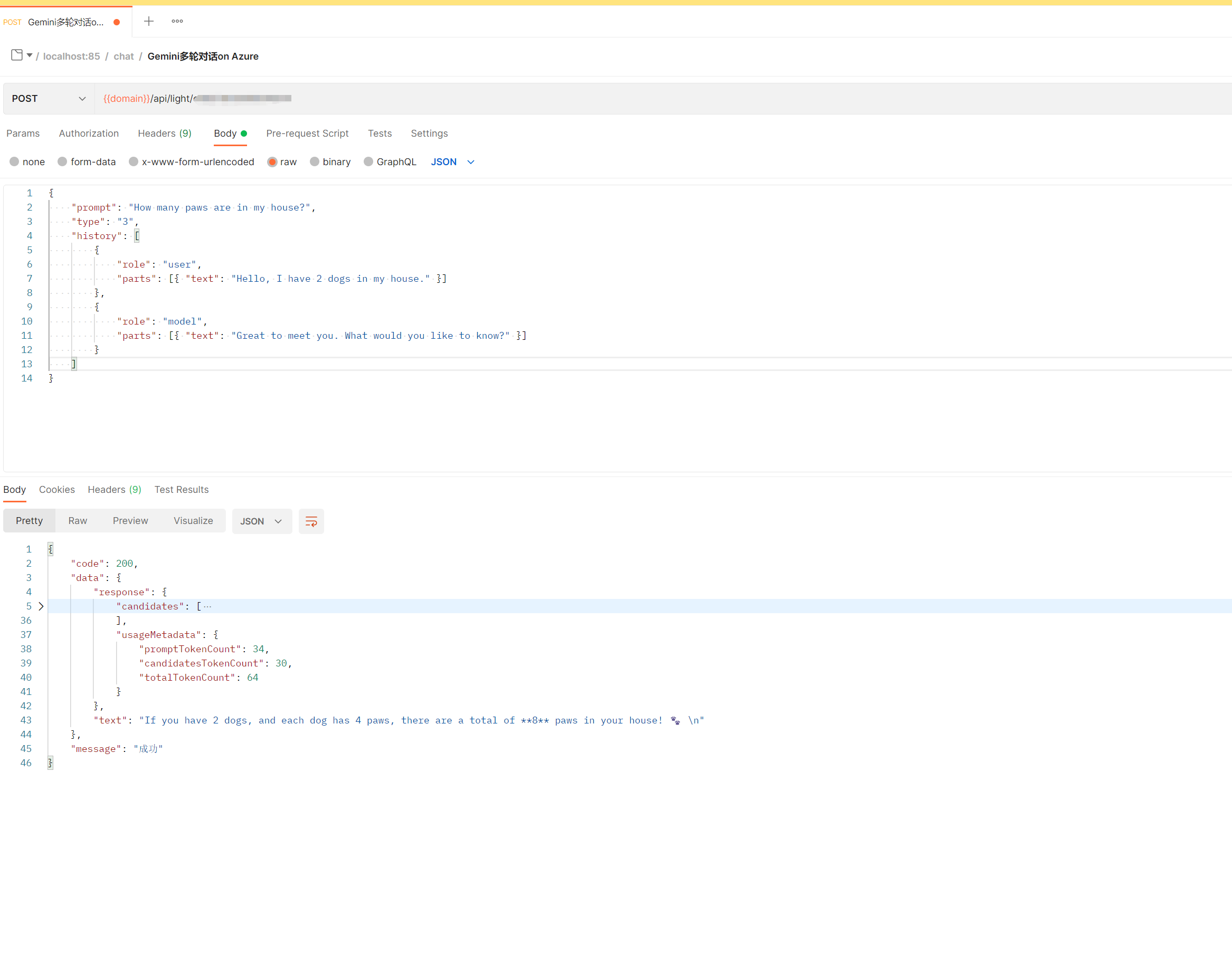
gemini 1.5 flash (node项目)
https://www.npmjs.com/package/google/generative-ai https://ai.google.dev/pricing?hlzh-cn https://aistudio.google.com/app/apikey https://ai.google.dev/gemini-api/docs/models/gemini?hlzh-cn#gemini-1.5-flash https://ai.google.dev/gemini-api/docs/get-started…...
在线字节大端序小端序转换器
具体请前往:在线字节大端序小端序转换器...

css_17_背景属性鼠标属性
一.背景属性 -属性值:background-color(设置背景颜色) 默认背景颜色是 transparent。 -属性值:background-image(设置背景图片) url(图片的地址) -属性值:background-re…...
)
Python hash编码(go hash编码)
id"中国人" 首先,go语言hash: import (mmh3 "murmurhash3") mmh3.Murmurhash3([]byte(id)) 对应到Python hash编码,可以直接使用mmh3 import mmh3 mmh3.hash(id,signedFalse) 其源码可以表示为 def sum32WithSeed(datas, seed…...
)
004 插入排序(lua)
文章目录 123 1 -- Lua中没有类和方法的概念,所以我们将所有功能都写在一个脚本中 -- 交换数组中两个元素的功能 local function swap(arr, i, j) local temp arr[i] arr[i] arr[j] arr[j] temp end -- 插入排序算法的实现 local function insertionS…...

计算机网络 —— 基本概念
基本概念 1. 通信协议2. 面向连接 v.s. 面向无连接3. 电路交换 v.s. 分组交换4. 单工通信 v.s. 双工通信 1. 通信协议 通信协议就是计算机与计算机之间通过网络实现通信时事先达成的一种“约定”。这种“约定”使那些由不同厂商的设备、不同的CPU 以及不同的操作系统组成的计算…...
高精度除法的实现
高精度除法与高精度加法的定义、前置过程都是大致相同的,如果想了解具体内容,可以移步至我的这篇博客:高精度加法计算的实现 在这里就不再详细讲解,只讲解主体过程qwq 主体过程 高精度除法的原理和小学学习的竖式除法是一样的。 …...

STM32CUBEMX配置USB虚拟串口
STM32CUBEMX配置USB虚拟串口 cubemx上默认配置即可。 外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传 配置完后生成工程,主要就是要知道串口的收发接口就行了。 发送:CDC_Transmit_FS(),同时记得包含头文件#include “…...

安卓开发中margin和padding的区别
在 Android 开发中,margin 和 padding 都是用来定义视图(View)的空间属性,但它们的作用和应用场景有所不同: Margin(外边距): Margin 是视图与其他视图之间的空间。它定义了视图之间…...

Symfony事件调度系统:掌控应用程序生命周期的钥匙
Symfony事件调度系统:掌控应用程序生命周期的钥匙 引言 Symfony是一个高度灵活的PHP框架,用于构建各种规模的Web应用程序。它的核心特性之一是事件调度系统,该系统允许开发者在应用程序的生命周期中触发和监听事件。这种机制为开发者提供了…...
maven安装jar和pom到本地仓库
举例子我们要将 elastic-job-spring-boot-starter安装到本地的maven仓库,如下: <dependency><groupId>com.github.yinjihuan</groupId><artifactId>elastic-job-spring-boot-starter</artifactId><version>1.0.5&l…...

[leetcode]assign-cookies. 分发饼干
. - 力扣(LeetCode) class Solution { public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(), g.end());sort(s.begin(), s.end());int m g.size(), n s.size();int count 0;for (int i 0, j 0; i…...

如何轻松解决复杂文档格式转换问题
上周,我遇到了一个棘手的问题:需要将一大堆PDF文件转换成可编辑的Word文档,时间紧迫,手动转换根本来不及。朋友推荐我使用了一个网站——xuelin.cc,这个网站不仅提供强大的AI对话功能,还能轻松完成各种文档…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
