Python hash编码(go hash编码)
id="中国人"
首先,go语言hash:
import (mmh3 "murmurhash3")
mmh3.Murmurhash3([]byte(id))对应到Python hash编码,可以直接使用mmh3
import mmh3
mmh3.hash(id,signed=False)其源码可以表示为
def sum32WithSeed(datas, seed=0):c1_32 = 0xcc9e2d51c2_32 = 0x1b873593h1 = seeddatas_bytes = datas.encode('utf-8')datas_bytes_len = len(datas_bytes)if datas_bytes_len == 0:return 0nblocks = datas_bytes_len // 4for id in range(datas_bytes_len):if id % 4 != 0 or id + 4 > datas_bytes_len:continuek1 = int.from_bytes(datas_bytes[id:id + 4], byteorder='little', signed=False)k1 *= c1_32k1 &= 0xffffffffk1 = (k1 << 15) | (k1 >> 17)k1 *= c2_32k1 &= 0xffffffffh1 ^= k1h1 = (h1 << 13) | (h1 >> 19)h1 = h1 * 4 + h1 + 0xe6546b64h1 &= 0xfffffffftail = datas_bytes[nblocks * 4:]tail_len = len(tail)k1 = 0for id in [3, 2, 1]:if tail_len >= id and id == 3:k1 ^= int.from_bytes(tail[2:3], byteorder='little', signed=False) << 16if tail_len >= id and id == 2:k1 ^= int.from_bytes(tail[1:2], byteorder='little', signed=False) << 8if tail_len >= id and id == 1:k1 ^= int.from_bytes(tail[0:1], byteorder='little', signed=False)k1 *= c1_32k1 &= 0xffffffffk1 = (k1 << 15) | (k1 >> 17)k1 *= c2_32k1 &= 0xffffffffh1 ^= k1h1 &= 0xffffffffh1 ^= datas_bytes_lenh1 ^= h1 >> 16h1 *= 0x85ebca6bh1 &= 0xffffffffh1 ^= h1 >> 13h1 *= 0xc2b2ae35h1 &= 0xffffffffh1 ^= h1 >> 16return h1def sum32(datas):return sum32WithSeed(datas, 0)print(sum32(id))
相关文章:
)
Python hash编码(go hash编码)
id"中国人" 首先,go语言hash: import (mmh3 "murmurhash3") mmh3.Murmurhash3([]byte(id)) 对应到Python hash编码,可以直接使用mmh3 import mmh3 mmh3.hash(id,signedFalse) 其源码可以表示为 def sum32WithSeed(datas, seed…...
)
004 插入排序(lua)
文章目录 123 1 -- Lua中没有类和方法的概念,所以我们将所有功能都写在一个脚本中 -- 交换数组中两个元素的功能 local function swap(arr, i, j) local temp arr[i] arr[i] arr[j] arr[j] temp end -- 插入排序算法的实现 local function insertionS…...

计算机网络 —— 基本概念
基本概念 1. 通信协议2. 面向连接 v.s. 面向无连接3. 电路交换 v.s. 分组交换4. 单工通信 v.s. 双工通信 1. 通信协议 通信协议就是计算机与计算机之间通过网络实现通信时事先达成的一种“约定”。这种“约定”使那些由不同厂商的设备、不同的CPU 以及不同的操作系统组成的计算…...
高精度除法的实现
高精度除法与高精度加法的定义、前置过程都是大致相同的,如果想了解具体内容,可以移步至我的这篇博客:高精度加法计算的实现 在这里就不再详细讲解,只讲解主体过程qwq 主体过程 高精度除法的原理和小学学习的竖式除法是一样的。 …...

STM32CUBEMX配置USB虚拟串口
STM32CUBEMX配置USB虚拟串口 cubemx上默认配置即可。 外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传 配置完后生成工程,主要就是要知道串口的收发接口就行了。 发送:CDC_Transmit_FS(),同时记得包含头文件#include “…...

安卓开发中margin和padding的区别
在 Android 开发中,margin 和 padding 都是用来定义视图(View)的空间属性,但它们的作用和应用场景有所不同: Margin(外边距): Margin 是视图与其他视图之间的空间。它定义了视图之间…...

Symfony事件调度系统:掌控应用程序生命周期的钥匙
Symfony事件调度系统:掌控应用程序生命周期的钥匙 引言 Symfony是一个高度灵活的PHP框架,用于构建各种规模的Web应用程序。它的核心特性之一是事件调度系统,该系统允许开发者在应用程序的生命周期中触发和监听事件。这种机制为开发者提供了…...
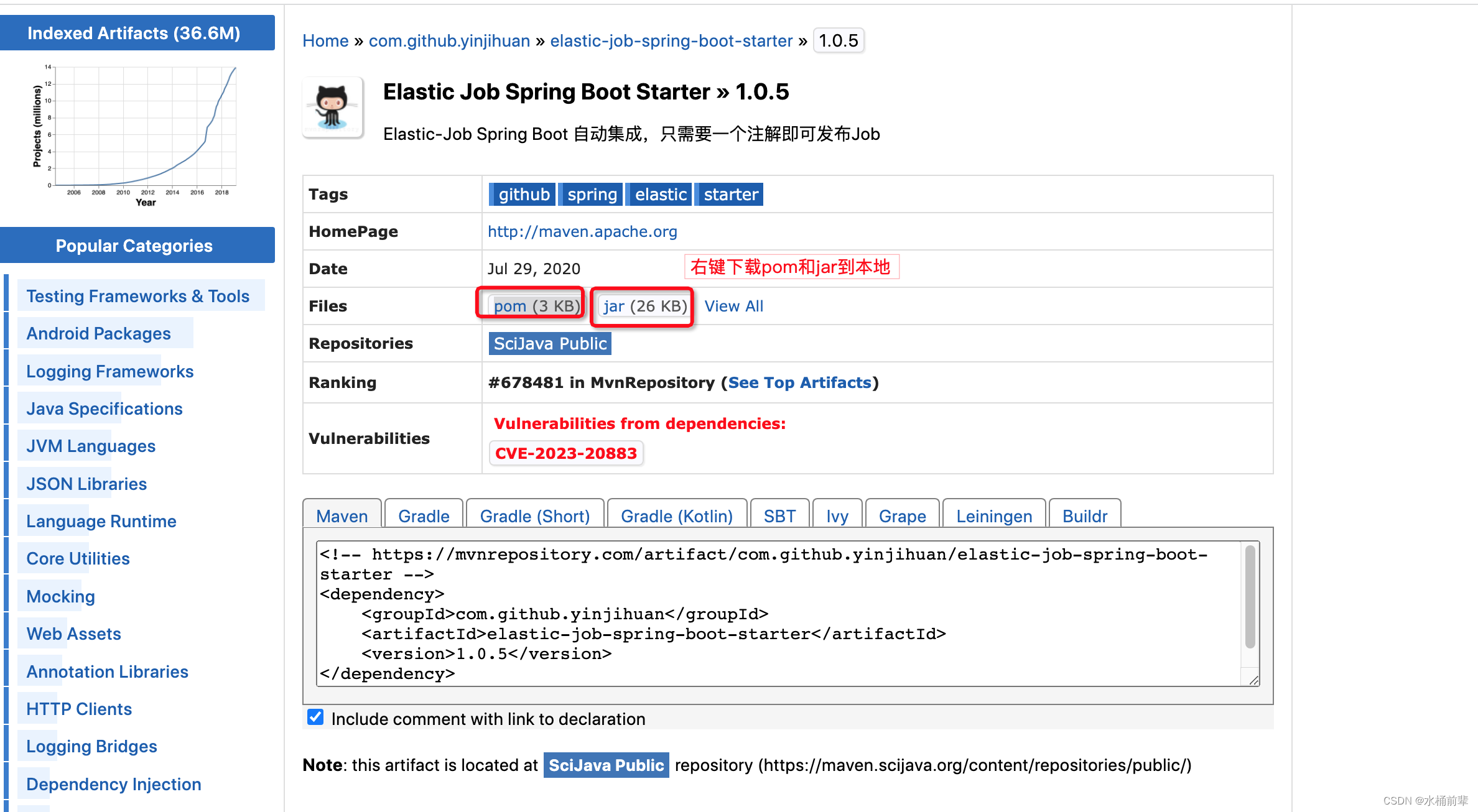
maven安装jar和pom到本地仓库
举例子我们要将 elastic-job-spring-boot-starter安装到本地的maven仓库,如下: <dependency><groupId>com.github.yinjihuan</groupId><artifactId>elastic-job-spring-boot-starter</artifactId><version>1.0.5&l…...

[leetcode]assign-cookies. 分发饼干
. - 力扣(LeetCode) class Solution { public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(), g.end());sort(s.begin(), s.end());int m g.size(), n s.size();int count 0;for (int i 0, j 0; i…...

如何轻松解决复杂文档格式转换问题
上周,我遇到了一个棘手的问题:需要将一大堆PDF文件转换成可编辑的Word文档,时间紧迫,手动转换根本来不及。朋友推荐我使用了一个网站——xuelin.cc,这个网站不仅提供强大的AI对话功能,还能轻松完成各种文档…...

日期类(java)
文章目录 第一代日期类 Date常用构造方法SimpleDateFormat 日期格式化类日期转字符串(String -> Date)字符串转日期 (String->Date) 第二代日期类 Calendar常用字段与如何得到实例对象相关 API 第三代日期类(LocalDate\TIme)日期,时间&…...

【深度学习】C++ Tensorrt Yolov8 目标检测推理
C Tensorrt Yolov8 目标检测推理 模型导出代码yolov8.hyolov8.cppcommon.hppCMakeListmain.cpp C tensorrt对yolov8目标检测模型进行推理。 Windows版本下只需要修改common.hpp对文件的判断S_ISREG 和对文件夹的判断S_ISDIR即可,非核心代码,不调用删掉都…...

【项目日记(二)】搜索引擎-索引制作
❣博主主页: 33的博客❣ ▶️文章专栏分类:项目日记◀️ 🚚我的代码仓库: 33的代码仓库🚚 🫵🫵🫵关注我带你了解更多项目内容 目录 1.前言2.索引结构2.1创捷索引2.2根据索引查询2.3新增文档2.4内存索引保存到磁盘2.5把…...

K 近邻、K-NN 算法图文详解
1. 为什么学习KNN算法 KNN是监督学习分类算法,主要解决现实生活中分类问题。根据目标的不同将监督学习任务分为了分类学习及回归预测问题。 KNN(K-Nearest Neihbor,KNN)K近邻是机器学习算法中理论最简单,最好理解的算法…...

Eclipse + GDB + J-Link 的单片机程序调试实践
Eclipse GDB J-Link 的调试实践 本文介绍如何创建Eclipse的调试配置,如何控制调试过程,如何查看修改各种变量。 对 Eclipse 的要求 所用 Eclipse 应当安装了 Eclipse Embedded CDT 插件。从 https://www.eclipse.org/downloads/packages/ 下载 Ecli…...

前端代码生成辅助工具
1,Axure Axure设计的界面如何生成HTML文件 https://blog.csdn.net/qq_43279782/article/details/112387511 Axure 生成HTML 文件,并用Chrome打开 https://blog.csdn.net/qq_30718137/article/details/80621025 2,OpenUI [开源] OpenUI …...

静态库与动态库总结
一、库文件和头文件 所谓库文件,可以将其理解为压缩包文件,该文件内部通常包含不止一个目标文件(也就是二进制文件)。 值得一提的是,库文件中每个目标文件存储的代码,并非完整的程序,而是一个…...

深入解析tcpdump:网络数据包捕获与分析的利器
引言 在网络技术日新月异的今天,网络数据包的捕获与分析成为了网络管理员、安全专家以及开发人员不可或缺的技能。其中,tcpdump作为一款强大的网络数据包捕获分析工具,广泛应用于Linux系统中。本文将从技术人的角度,详细分析tcpdu…...

【漏洞复现】科立讯通信有限公司指挥调度管理平台uploadgps.php存在SQL注入
0x01 产品简介 科立讯通信指挥调度管理平台是一个专门针对通信行业的管理平台。该产品旨在提供高效的指挥调度和管理解决方案,以帮助通信运营商或相关机构实现更好的运营效率和服务质量。该平台提供强大的指挥调度功能,可以实时监控和管理通信网络设备、…...
什么是自然语言处理(NLP)?详细解读文本分类、情感分析和机器翻译的核心技术
什么是自然语言处理? 自然语言处理(Natural Language Processing,简称NLP)是人工智能的一个重要分支,旨在让计算机理解、解释和生成人类的自然语言。打个比方,你和Siri对话,或使用谷歌翻译翻译一…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
