当前位置： 首页 > news >正文

Windows 中的 Hosts 文件是什么？如何找到并修改它？

news 2026/2/6 22:23:12

什么是 Hosts 文件

Hosts 文件是一个纯文本文件，存在于几乎所有的操作系统中，用于将主机名映射到 IP 地址。在域名系统（DNS）尚未普及之前，Hosts 文件是计算机网络中唯一用于主机名解析的方式。随着网络规模的扩大和 DNS 的引入，Hosts 文件逐渐退居次要位置，但它仍然是一个重要的工具，特别是在网络配置和故障排除中。

那 Windows Hosts 文件在哪？一般这个文件存放在“C:\Windows\System32\drivers\etc\hosts”中。

Hosts 文件用途

在了解了 Hosts 文件是什么之后我们再来看一看 Hosts 文件的用处都有哪些。

Hosts 文件的主要作用是进行主机名解析，即将可读的主机名转换为计算机可识别的 IP 地址。当在浏览器中输入一个网址时，系统会首先检查 Hosts 文件，看是否有相应的主机名映射，如果有就直接使用该映射，而无需查询 DNS 服务器。

它还可以屏蔽某些网站，可以将某些网站的主机名映射到一个无效的 IP 地址，在局域网中还可以使用该文件为本地设备设置静态 IP 地址映射，加快访问速度。

Hosts 文件还可以用于将流量重定向到特定的服务器。这在开发和测试环境中非常有用，允许开发人员在不影响生产环境的情况下进行测试。

如何编辑

因为 Hosts 文件是系统文件，所以我们需要使用管理员权限才能去修改它，下面是具体的操作步骤：

首先我们可以找到记事本工具，然后使用管理员身份运行。

然后在点击记事本中的文件，按照上面的文件地址（C:\Windows\System32\drivers\etc）找到 Hosts 文件，打开之后如果看见文件夹是空的记得修改下方选择框中的文件类型。

打开 Hosts 文件之后就可以自行在文件中添加一些映射，然后保存之后退出记事本就可以实现 Hosts 文件的修改操作。

当然你也可以在修改之前将 Hosts 文件进行备份，如果修改出现问题也可以直接使用备份的文件替换错误文件。

除了使用记事本之外，还可以使用命令提示符来修改 Hosts 文件，我们同样的需要使用管理员身份来运行命令提示符。

然后输入命令“echo 127.0.0.2 google.com >> %SystemRoot%\System32\drivers\etc\hosts”

接下来输入“type %SystemRoot%\System32\drivers\etc\hosts”我们就可以看见修改之后的 Hosts 文件。

原文链接：Windows 中的 Hosts 文件是什么？如何找到并修改它？ 

相关文章：

Windows 中的 Hosts 文件是什么？如何找到并修改它？

什么是 Hosts 文件 Hosts 文件是一个纯文本文件，存在于几乎所有的操作系统中，用于将主机名映射到 IP 地址。在域名系统（DNS）尚未普及之前，Hosts 文件是计算机网络中唯一用于主机名解析的方式。随着网络规模的扩大和 D…...

编程日记 2024/6/30 4:38:34

详细分析Oracle中的tnsnames.ora基本知识 以及 PLSQL如何连接（附Demo）

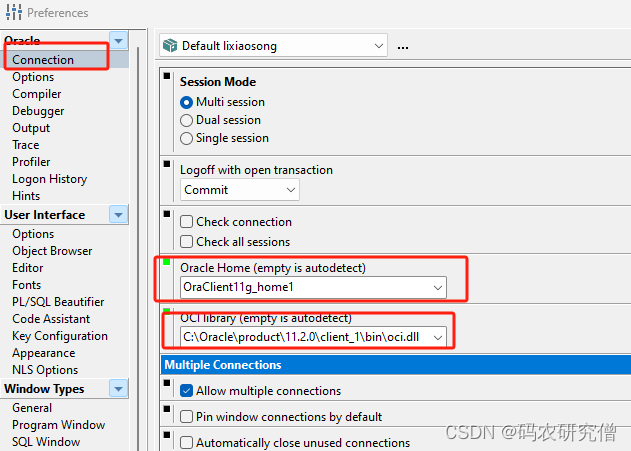
目录 1. tnsnames.ora2. Demo3. 实战 1. tnsnames.ora Oracle 数据库网络配置文件，用于配置客户端与数据库服务器之间的连接 定义网络服务名称，客户端可以使用这些名称连接到数据库实例 基本的路径如下： Windows: ORACLE_HOME\network\ad…...

编程日记 2024/6/30 4:37:33

[深度学习] 图神经网络GNN

图神经网络（Graph Neural Network, GNN）是一类用于处理图结构数据的深度学习模型。图是一种重要的数据结构，广泛应用于社交网络、分子化学、推荐系统、交通网络等领域。GNN的出现使得能够有效地在图结构数据上进行学习和推理。以下是GNN的详细…...

编程日记 2024/6/30 4:35:30

MATLAB中添加 Git 子模块

目录 更新子模块 对子模块使用提取和合并 使用推送将更改发送到子模块存储库 要重用其他存储库中的代码，可以指定 Git™ 子模块。 要将外部 Git 存储库克隆为子模块，请执行以下操作： 在 MATLAB 当前文件夹浏览器中点击右键，然…...

编程日记 2024/6/30 4:31:27

24级中国科学技术大学843信号与系统考研分数线，中科大843初复试科目，参考书，大纲，真题，苏医工生医电子信息与通信工程。

(上岸难度：★★★★☆，考试大纲、真题、经验帖等考研资讯和资源加群960507167/博睿泽电子信息通信考研咨询：34342183) 一、专业目录及考情分析 说明: ①复试成绩:满分100分。上机满分50分，面试满分150分，复试成绩(上机…...

编程日记 2024/6/30 4:29:24

深入剖析C语言中volatile与register关键字的实战应用与底层原理

引言 C语言以其贴近硬件的特性，赋予了开发者强大的底层控制能力。在众多关键字中，"volatile" 和 "register" 是两个具有特殊意义的关键字，它们直接影响着编译器对程序语句的处理逻辑，从而影响程序的正确性和…...

编程日记 2024/6/30 4:27:22

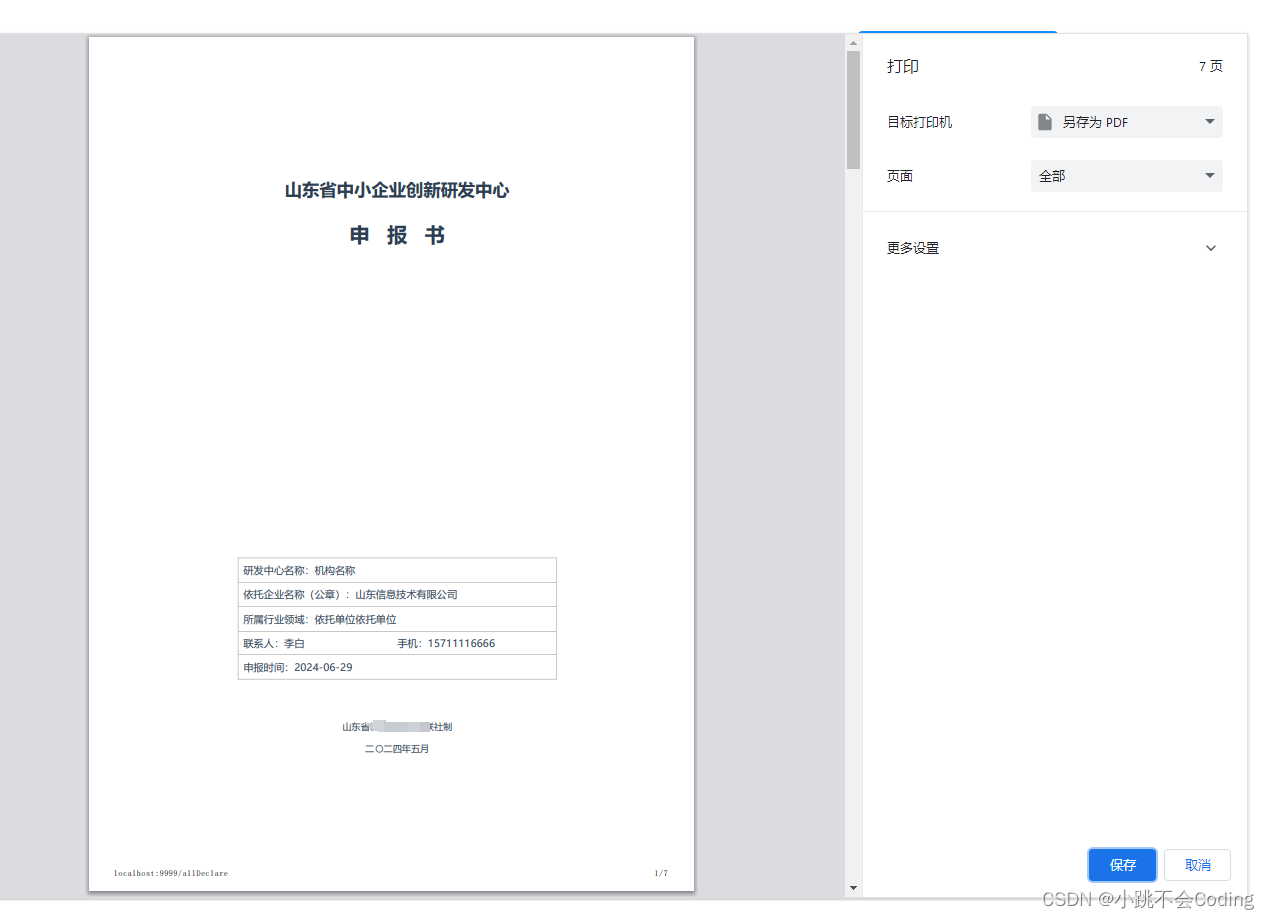
vue开发网站--关于window.print()调取打印

1.vue点击按钮调取打印 点击按钮&#xff1a; 调取打印该页面&#xff1a; <div click"clickDown()">下载</div>methods: {//下载-调取打印clickDown() {window.print()}, }<style>/* 点击打印的样式 */media print {.clickDown {display: no…...

编程日记 2024/6/30 4:25:21

OJ-选座位

题目描述 要考试了&#xff0c;小明需要去图书馆挑选一个座位来复习。小明需要找到一个位置&#xff0c;这个位置应距离任何已经落座的人尽可能的远&#xff08;即与最近的人的距离尽可能的大&#xff09;。 图书馆的座位为一个N*M的矩阵&#xff0c;N表示总的排数&#xff0…...

编程日记 2024/6/30 4:23:19

【子串】3. 无重复的最长子串

3. 无重复的最长子串 难度&#xff1a;中等难度 力扣地址&#xff1a;https://leetcode.cn/problems/longest-substring-without-repeating-characters/description/ 题目看起来简单&#xff0c;刷起来有好几个坑&#xff0c;特此记录一下&#xff0c;解法比官网的更加简单&…...

编程日记 2024/6/30 4:22:18

Scrapy中爬虫优化技巧分享

scrapy是一个非常有用的python爬虫框架&#xff0c;它可以帮助我们轻松地从不同的网站上获取数据。同时&#xff0c;scrapy也有越来越多的用户在使用它来爬取数据&#xff0c;因此&#xff0c;在使用scrapy的过程中&#xff0c;我们需要考虑如何优化我们的爬虫&#xff0c;以便…...

编程日记 2024/6/30 4:21:17

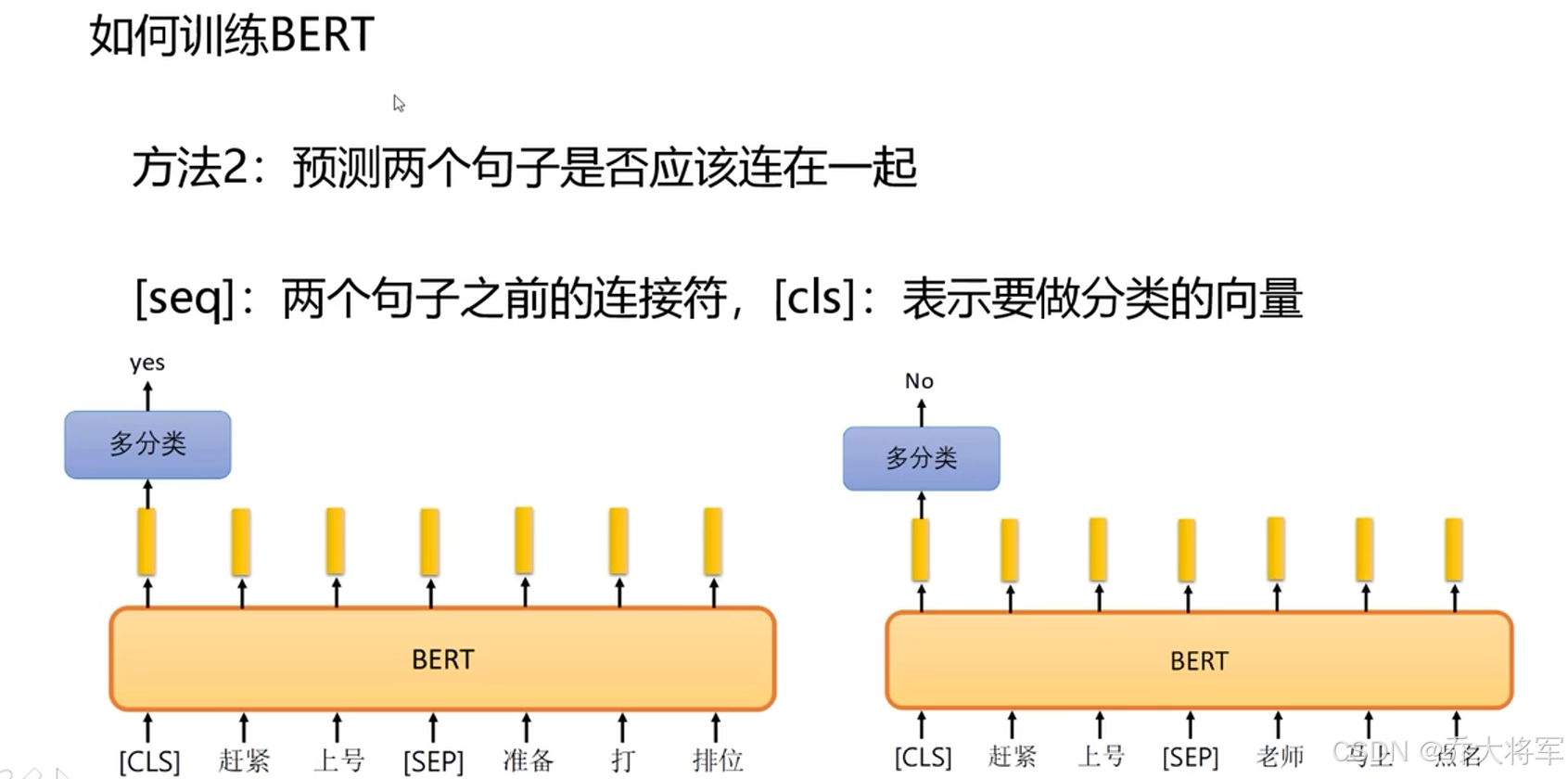
自然语言处理-BERT处理框架-transformer

目录 1.介绍 2.Transformer 2.1 引言 2.2 传统RNN网络的问题 2.3 整体架构 2.4 Attention 2.5 Self-Attention如何计算 3.multi-headed机制 4. BERT训练方法 1.介绍 BERT&#xff1a;当前主流的解决框架&#xff0c;一站式搞定NLP任务。&#xff08;解决一个NLP任务时的考虑…...

编程日记 2024/6/30 4:20:16

Kafka~消息系列问题解决：消费顺序问题解决、消息丢失问题优化（不能保证100%）

消息消费顺序问题 使用消息队列的过程中经常有业务场景需要严格保证消息的消费顺序&#xff0c;比如我们同时发了 2 个消息&#xff0c;这 2 个消息对应的操作分别对应的数据库操作是&#xff1a; 用户等级升级。根据用户等级下的订单价格 假如这两条消息的消费顺序不一样造…...

编程日记 2024/6/30 4:19:15

如何确保日常安全运维中的数据加密符合等保2.0标准？

等保2.0标准下的数据加密要求 等保2.0标准是中国信息安全等级保护制度的升级版&#xff0c;它对信息系统的安全保护提出了更为严格的要求。在日常安全运维中&#xff0c;确保数据加密符合等保2.0标准&#xff0c;主要涉及以下几个方面&#xff1a; 数据加密技术的选择&#xff…...

编程日记 2024/6/30 4:17:13

下一代的JDK - GraalVM

GraalVM是最近几年Java相关的新技术领域不多的亮点之一&#xff0c; 被称之为革命性的下一代JDK&#xff0c;那么它究竟有什么神奇之处&#xff0c;又为当前的Java开发带来了一些什么样的改变呢&#xff0c;让我们来详细了解下 下一代的JDK 官网对GraalVM的介绍是 “GraalVM 是…...

编程日记 2024/6/30 4:16:12

Java三方库-单元测试

文章目录 Junit注解常用类无参数单测带参数的单测 Junit 主要版本有4和5版本&#xff0c;注解不太一样&#xff0c; 4迁移5参考官方文档 主要记录下常用的一些操作 其他复杂操作见官网 https://junit.org/junit5/docs/current/user-guide/#overview-java-versions 引入5.9…...

编程日记 2024/6/30 4:15:11

p2p、分布式，区块链笔记: libp2p基础

通信密钥 noise::{Keypair, X25519Spec} X25519/Ed25519类似RSA 算法。Noise 用于设计和实现安全通信协议。它允许通信双方在没有预先共享密钥的情况下进行安全的密钥交换&#xff0c;并通过加密和身份验证保护通信内容。libp2p 提供了对 Noise 协议的原生支持&#xff0c;它允…...

编程日记 2024/6/30 4:13:10

企业本地大模型用Ollama+Open WebUI+Stable Diffusion可视化问答及画图

最近在尝试搭建公司内部用户的大模型，可视化回答，并让它能画图出来， 主要包括四块： Ollama 管理和下载各个模型的工具Open WebUI 友好的对话界面Stable Diffusion 绘图工具Docker 部署在容器里，提高效率以上运行环境Win10, Ollama,SD直接装在windows10下， 然后安装Docker…...

编程日记 2024/6/30 4:11:06

Unity学习笔记---调试

使用Log进行调试 使用Debug.Log方法可以将一些运行时信息打印到Console窗口中。 打印时间戳 //获取时间 Debug.Log(DateTime.Now.ToString());//打印毫秒级的时间 Debug.Log(((DateTime.Now.ToUniversalTime().Ticks - 621355968000000000) / 10000) * 0.001); 打印自定义文…...

编程日记 2024/6/30 4:10:05

Py之dashscope：dashscope的简介、安装和使用方法、案例应用之详细攻略

Py之dashscope&#xff1a;dashscope的简介、安装和使用方法、案例应用之详细攻略 目录 dashscope的简介 1、产品的主要特点和优势包括&#xff1a; dashscope的安装和使用方法 1、安装 2、使用方法 dashscope的案例应用 1、通义千问-Max&#xff1a;通义千问2.5系列 2…...

编程日记 2024/6/30 4:09:04

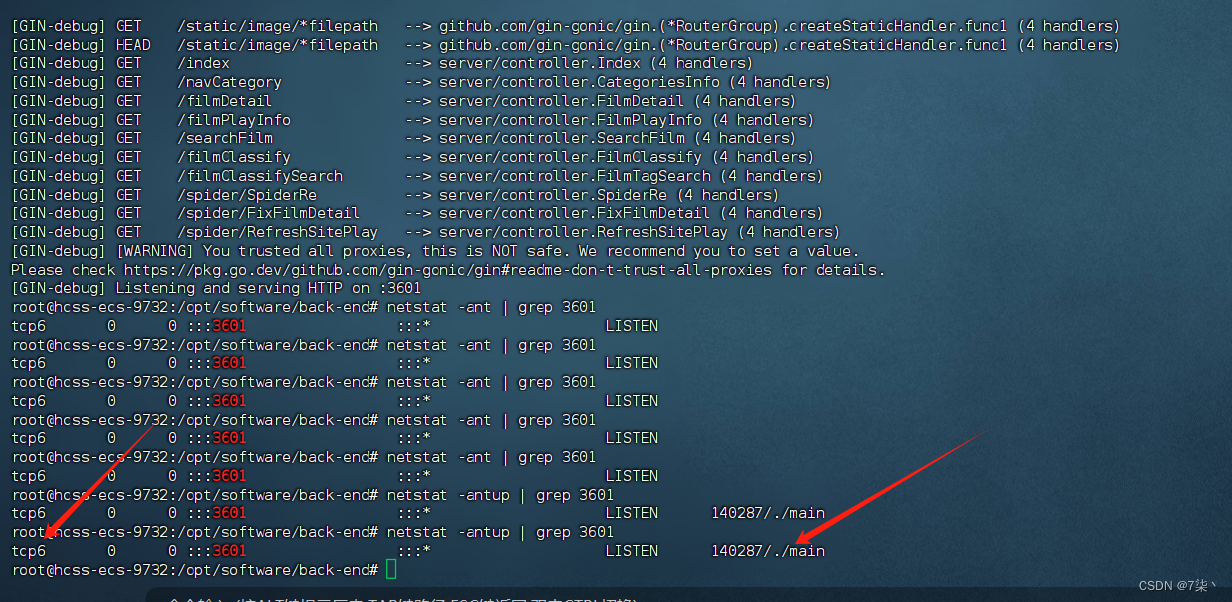
Go使用Gin框架开发的Web程序部署在Linux时，无法绑定监听Ipv4端口

最近有写一部分go语言开发的程序&#xff0c;在部署程序时发现&#xff0c;程序在启动后并没有绑定ipv4的端口&#xff0c;而是直接监听绑定ipv6的端口。 当我用netstat -antup | grep 3601查找我的gin服务启动的端口占用情况的时候发现&#xff0c;我的服务直接绑定了tcp6 &a…...

编程日记 2024/6/30 4:06:01

生成xcframework

打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式&#xff0c;可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

编程新知 2025/10/5 2:30:38

云原生核心技术 (7/12): K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？

大家好&#xff0c;欢迎来到《云原生核心技术》系列的第七篇&#xff01; 在上一篇&#xff0c;我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在&#xff0c;我们就像一个拥有了一块崭新数字土地的农场主&#xff0c;是时…...

编程新知 2025/12/14 22:32:59

大语言模型如何处理长文本？常用文本分割技术详解

为什么需要文本分割？ 引言：为什么需要文本分割？一、基础文本分割方法1. 按段落分割（Paragraph Splitting）2. 按句子分割（Sentence Splitting）二、高级文本分割策略3. 重叠分割（Sliding Window）4. 递归分割（Recursive Splitting）三、生产级工具推荐5. 使用LangChain的…...

编程新知 2025/11/18 0:32:13

【算法训练营Day07】字符串part1

文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接&#xff1a;344. 反转字符串 双指针法&#xff0c;两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

编程新知 2025/8/27 14:38:58

Java 加密常用的各种算法及其选择

在数字化时代&#xff0c;数据安全至关重要&#xff0c;Java 作为广泛应用的编程语言&#xff0c;提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景&#xff0c;有助于开发者在不同的业务需求中做出正确的选择。​ 一、对称加密算法…...

编程新知 2025/11/22 20:41:02

用docker来安装部署freeswitch记录

今天刚才测试一个callcenter的项目&#xff0c;所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

编程新知 2026/2/1 3:20:44

基于Java+VUE+MariaDB实现（Web）仿小米商城

仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意&#xff1a;运行前…...

编程新知 2026/1/31 4:37:40

关于uniapp展示PDF的解决方案

在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项&#xff1a; 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库&#xff1a; npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

编程新知 2025/9/18 20:16:52

沙箱虚拟化技术虚拟机容器之间的关系详解

问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西&#xff0c;但是如果把三者放在一起&#xff0c;它们之间到底什么关系&#xff1f;又有什么联系呢&#xff1f;我不是很明白&#xff01;&#xff01;&#xff01; 就比如说&#xff1a; 沙箱&#…...

编程新知 2026/2/6 6:05:52

Python学习(8) ----- Python的类与对象

Python 中的类&#xff08;Class&#xff09;与对象&#xff08;Object&#xff09;是面向对象编程&#xff08;OOP&#xff09;的核心。我们可以通过“类是模板&#xff0c;对象是实例”来理解它们的关系。 &#x1f9f1; 一句话理解&#xff1a; 类就像“图纸”&#xff0c;对…...

编程新知 2025/10/23 12:11:37