LeetCode:494. 目标和
题目
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
思路
方法一:使用递归
方法二:使用动态规划,记数组的元素和为 sum,添加 - 号的元素之和为 a,则其余添加 + 的元素之和为 sum−a,得到的表达式的结果为(sum-a)-a = sum - 2a = target , res != -1检查memo数组是否已缓存了该子问题的解。如果有直接返回,c < nums[i]表示当前元素值大于负载值,无法选择当前元素。直接递归处理下一元素,如果negatives无法选择当前元素,考虑两种选择: 1,不选择当前元素,递归处理下一元素dfs(dfs, i-1, c) 。 2,选择当前元素,负载减去该元素值,递归dfs(dfs, i-1, c-nums[i]),则两种选择的方案数相加就是包含和不包含当前元素的总方案数。
代码
方法一
class Solution {
public:int count = 0;int findTargetSumWays(vector<int>& nums, int target) {backtrack(nums, target, 0, 0);return count;}void backtrack(vector<int>& nums, int target, int index, int sum) {if (index == nums.size()) {if (sum == target) {count++;}} else {backtrack(nums, target, index + 1, sum + nums[index]);backtrack(nums, target, index + 1, sum - nums[index]);}}
};方法二
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int s = reduce(nums.begin(), nums.end(), 0) - abs(target);if (s < 0 || s % 2)return 0;int m = s / 2;int n = nums.size();vector<vector<int>> memo(n, vector<int>(m + 1, -1));auto dfs = [&](auto&& dfs, int i, int c) -> int {if (i < 0)return c == 0;int& res = memo[i][c];if (res != -1)return res;if (c < nums[i]) {return res = dfs(dfs, i - 1, c);}return res = dfs(dfs, i - 1, c) + dfs(dfs, i - 1, c - nums[i]);};return dfs(dfs, n - 1, m);}
};
总结
- 使用回溯可以遍历不同的方案,
- 问题转化成在数组 nums 中选取若干元素,使得这些元素之和等于 ’ - ’ 次数,计算选取元素的方案数,就可以使用动态规划了
相关文章:

LeetCode:494. 目标和
题目 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 ‘’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ‘’ ,在 1 之前添…...

HarmonyOS Next开发学习手册——选项卡 (Tabs)
当页面信息较多时,为了让用户能够聚焦于当前显示的内容,需要对页面内容进行分类,提高页面空间利用率。 Tabs 组件可以在一个页面内快速实现视图内容的切换,一方面提升查找信息的效率,另一方面精简用户单次获取到的信息…...

LeetCode2710.移除字符串中的尾随零
cpp class Solution { public:string removeTrailingZeros(string num) {int flag 0;string s num;int size num.length();for (int i num.length() - 1; i > 0; i--) {if (num[i] ! 0)break;if (num[i] 0) {size--;}}s.resize(size);return s;} };...
PPT录屏怎么录?PPT录屏,3种方法简单操作
在数字化时代,PPT已经成为我们日常工作、学习和生活中不可或缺的一部分。无论是商务报告、教学课件还是产品展示,PPT都能帮助我们更加生动、直观地传递信息。然而,有时候我们会面临PPT录屏怎么录的问题。这时,一个好的PPT录屏功能…...

HarmonyOS开发:应用完整性校验
简介 为了确保应用的完整性和来源可靠,OpenHarmony需要对应用进行签名和验签。 应用开发阶段: 开发者完成开发并生成安装包后,需要开发者对安装包进行签名,以证明安装包发布到设备的过程中没有被篡改。OpenHarmony的应用完整性校…...

【MySQL基础篇】SQL指令:DQL及DCL
1、DQL DQL - 介绍 DQL英文全称是Data Query Language(数据查询语言),数据查询语言,用来查询数据表中的记录。(在MySQL中应用是最为广泛的) 查询关键字:SELECT DQL - 语法 SELECT 字段列表 FROM 表名列表 WHER…...
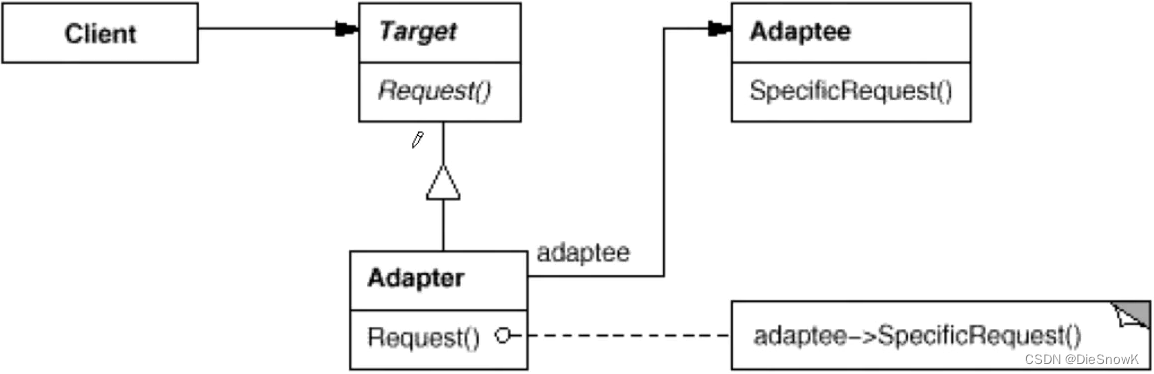
[C++][设计模式][适配器模式]详细讲解
目录 1.动机2.模式定义3.要点总结4.代码感受 1.动机 在软件系统中,由于应用环境的变化,常常需要将”一些现存的对象“放在新的环境中应用,但是新环境要求的接口是这些现存对象所不满足如何应对这些”迁移的变化“?如何既能利用现…...

8080时序驱动TFT显示屏 驱动IC GC9307
8080时序总共有控制线 CS片选线 DC(命令数据控制线) RD读控制线 WR写控制线 和N条数据线。 控制底层代码如下; 写读代码,读的代码反过来就行 inline void TFT8080WriteDat(unsigned char dat) {CS_L;//开始片选DC_H;//写数据 // RD_H;//禁止读WR_H;//禁止写WR_L;//写入…...

K8S 集群节点缩容
环境说明: 主机名IP地址CPU/内存角色K8S版本Docker版本k8s231192.168.99.2312C4Gmaster1.23.1720.10.24k8s232192.168.99.2322C4Gwoker1.23.1720.10.24k8s233(需下线)192.168.99.2332C4Gwoker1.23.1720.10.24 1. K8S 集群节点缩容 当集群中有…...

Web-HTML-事件
1 需求 2 语法 3 示例 4 参考资料 HTML 事件 | 菜鸟教程...
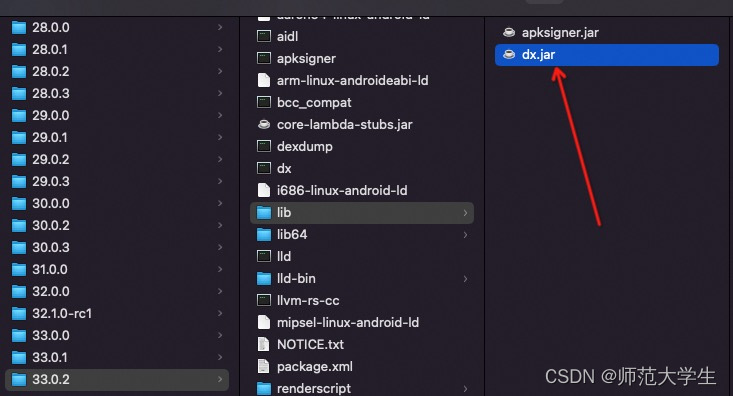
Installed Build Tools revision xxx is corrupted. Remove and install again 解决
1.在buildTools文件下找到对应的sdk版本,首先将版本对应目录下的d8.bat改名为dx.bat。 2.在lib文件下将d8.jar改名为dx.jar。 3.重新编译工程即可...

AI 与 Python 实战干货:基于深度学习的图像识别
《AI 与 Python 实战干货:基于深度学习的图像识别》 今天咱不啰嗦,直接上干货! 在 AI 领域,特别是图像识别方面,Python 简直是一把利器。咱就以手写数字识别为例,来看看怎么用 Python 实现一个深度学习模…...

万字长文详解数据结构:树 | 第6章 | Java版大话数据结构 | 二叉树 | 哈夫曼树 | 二叉树遍历 | 构造二叉树 | LeetCode练习
📌本篇分享的大话数据结构中🎄树🎄这一章的知识点,在此基础上,增加了练习题帮助大家理解一些重要的概念✅;同时,由于原文使用的C语言代码,不利于学习Java语言的同学实践,…...
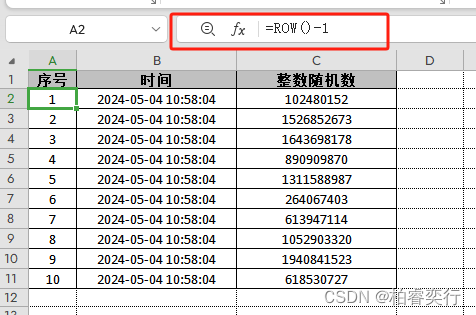
NPOI入门指南:轻松操作Excel文件的.NET库
目录 引言 一、NPOI概述 二、NPOI的主要用途 三、安装NPOI库 四、NPOI基本使用 六、性能优化和内存管理 七、常见问题与解决方案 八、结论 附录 引言 Excel文件作为数据处理的重要工具,广泛应用于各种场景。然而,在没有安装Microsoft Office的…...
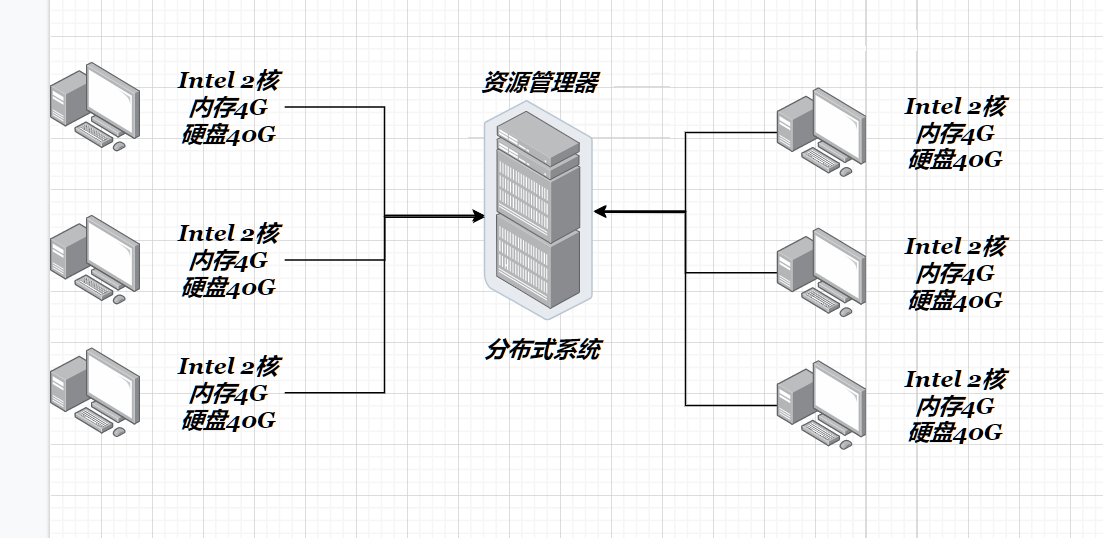
【高性能服务器】服务器概述
🔥博客主页: 我要成为C领域大神🎥系列专栏:【C核心编程】 【计算机网络】 【Linux编程】 【操作系统】 ❤️感谢大家点赞👍收藏⭐评论✍️ 本博客致力于知识分享,与更多的人进行学习交流 服务器概述 服…...

003 SSM框架整合
文章目录 整合web.xmlapplicationContext-dao.xmlapplicationContext-service.xmlspringmvc.xmldb.propertieslog4j.propertiespom.xml 测试sqlItemController.javaItemMapper.javaItem.javaItemExample.javaItemService.javaItemServiceImpl.javaItemMapper.xml 整合 将工程的…...
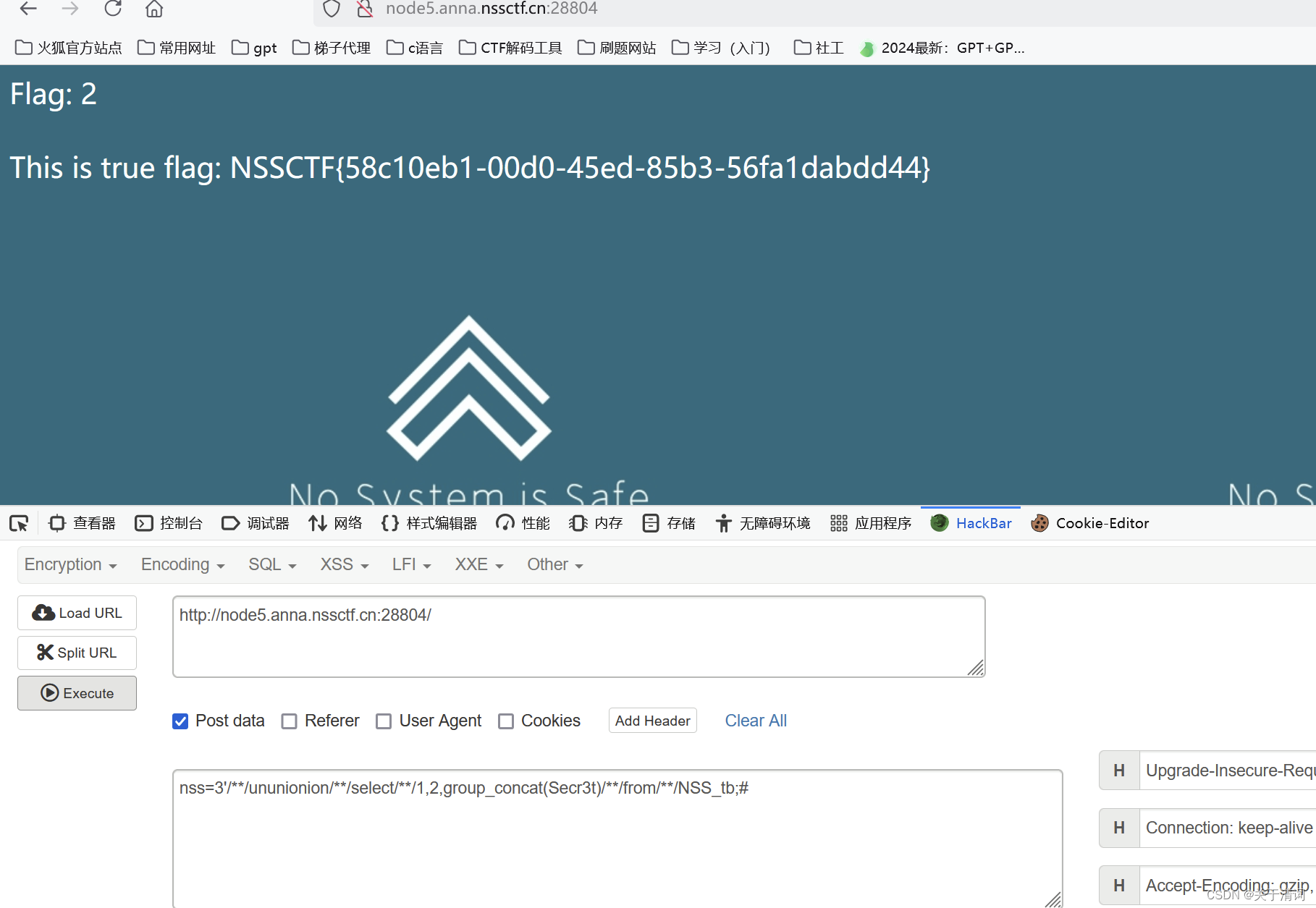
web刷题记录(7)
[HDCTF 2023]SearchMaster 打开环境,首先的提示信息就是告诉我们,可以用post传参的方式来传入参数data 首先考虑的还是rce,但是这里发现,不管输入那种命令,它都会直接显示在中间的那一小行里面,而实际的命令…...
【单片机毕业设计选题24037】-基于STM32的电力系统电力参数无线监控系统
系统功能: 系统上电后,OLED显示“欢迎使用电力监控系统请稍后”,两秒后显示“Waiting..”等待ESP8266初始化完成, ESP8266初始化成功后进入正常页面显示, 第一行显示电压值(单位V) 第二行显示电流值&am…...

Python使用彩虹表来尝试对MD5哈希进行破解
MD5是一种散列算法,它是不可逆的,无法直接解密。它的主要作用是将输入数据进行散列,生成一个固定长度的唯一哈希值。 然而,可以使用预先计算好的MD5哈希值的彩虹表(Rainbow Table)来尝试对MD5进行破解。彩…...
数据恢复篇: 如何在数据丢失后恢复照片
数据丢失的情况并不少见。如果您曾经遇到过图像丢失的情况,您可能想过照片恢复工具是如何工作的?可能会丢失多少数据图像?即使是断电也可能导致照片和媒体文件丢失。 话虽如此,如果你认为删除的照片无法恢复,那你就错…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
