【代码随想录训练营】【Day39】第九章|动态规划|62.不同路径|63. 不同路径 II
不同路径
题目详细:LeetCode.62
有点简单呀,做类似这种题型时,最好就是先画图:
- 可以像题目一样,画一个二维表格,表格内的值代表到达这个格子的不同路径总数
- 那么已知,如果图的大小为
m == 1 || n == 1时,即只有一列或一行时,那么其不同路径总数都只有一条 - 当出现其他情况时,我们并不难发现格子内的数值刚好等于其上边和左边格子的和,即其不同路径总数为经过上边和左边格子的不同路径之和
- 那么我们以此规律就可以依次计算出除第一列和第一行外,到达其他各个格子的不同路径数目
- 最后我们即可得到右下角终点的值,即为到达终点的不同路径总数
详细的解题思路我都写在注释里了,也可查阅:《代码随想录》— 不同路径
Java解法(动态规划):
class Solution {public int uniquePaths(int m, int n) {// 只有一列或一行时,那么其不同路径总数都只有一条if(m == 1 || n == 1){return 1;}// 主要初始化第一行和第一列的不同路径数都为1int[][] map = new int[m][n];for(int i = 0; i < m; i++){Arrays.fill(map[i], 1);}// 动态规划:从左往右,从上往下,计算到达每一个格子的不同路径总数for(int i = 1, j = 1; i < m;){// 递推公式map[i][j] = map[i - 1][j] + map[i][j - 1];// 先从左往右j++;if(j == n){// 到达右边界后,初始化列的下标j = 1;// 从上往下i++;}}return map[m - 1][n - 1];}
}
不同路径 II
题目详细:LeetCode.63
与上一题的区别在于这道题增加了障碍物,不过思路也不难,只要注意以下几点:
- 如果起点或终点出现了障碍物,则最终的不同路径总数都为0
- 对于第一列和第一行的初始化,按照从左往右,从上往下的顺序依次初始化为1,如果路径中出现了障碍物,则说明此路不通,后续的格子都初始化为0
- 将有障碍物的格子的不同路径总数记作0,只有遇到无障碍物的格子才累计其不同路径数目
那么只要根据以上三点,进行相对应的逻辑处理即可,累计格子的不同路径数目的思路与上一题的思路无异,详细的解题思路我都写在注释里了,也可查阅:《代码随想录》— 不同路径 II
Java解法(动态规划):
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length, n = obstacleGrid[0].length;// 特判,当障碍物出现在终点或起点时,不同路径总数都为0if(obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1){return 0;}// 定义一个辅助二维数组dp,防止直接操作原数组时,出现obstacleGrid[i][j] == 1的情况,将障碍物的表示数值累加进路径总数中int[][] dp = new int[m][n];// 对第一列和第一行进行赋值,路径总数为1,但是当路线上出现障碍物时,其后续的格子的路径总数都为0for(int i = 0; i < m && obstacleGrid[i][0] == 0; i++){dp[i][0] = 1;}for(int j = 0; j < n && obstacleGrid[0][j] == 0; j++){dp[0][j] = 1;}// 从左往右,从上往下记录到达每个格子的不同路径数目// 这里利用二维数组dp来记录到达各个格子的路径总数// 而obstacleGrid相当于地图,仅用于判断是否出现障碍物for(int i = 1, j = 1; i < m;){if(i >= m || j >= n) break;// 格子没障碍物才进行累计,有障碍物的格子其路径总数默认为0if(obstacleGrid[i][j] == 0)dp[i][j] = dp[i - 1][j] + dp[i][j - 1];if(n == ++j){j = 1;i++;}}return dp[m - 1][n - 1];}
}
相关文章:

【代码随想录训练营】【Day39】第九章|动态规划|62.不同路径|63. 不同路径 II
不同路径 题目详细:LeetCode.62 有点简单呀,做类似这种题型时,最好就是先画图: 可以像题目一样,画一个二维表格,表格内的值代表到达这个格子的不同路径总数那么已知,如果图的大小为m 1 || n…...

【Linux】linux | 修改系统编码 | 增加字体处理 | 图片处理字体变成方块
一、说明1、CentOS7二、修改系统编码编辑文件vi /etc/locale.conf修改编码并保存LANGzh_CN.UTF-8配置生效source /etc/locale.conf1)修改系统编码,只是让系统支持中文编码2)不解决文字不显示的问题;往后看三、解决字体不显示问题非…...

R语言介绍及安装教程
R语言是一种免费的开源编程语言和环境,主要用于数据分析、统计建模和可视化。它可以运行在不同的操作系统上,如Windows、MacOS和Linux。R语言具有以下特点:丰富的数据处理和统计分析函数库;易于学习和使用;可以生成高质…...

Linux 练习九 (IPC 消息队列)
文章目录消息队列有亲缘关系的进程使用消息队列通信无亲缘关系的进程使用消息队列通信使用环境:Ubuntu18.04 使用工具:VMWare workstations ,xshell作者在学习Linux的过程中对常用的命令进行记录,通过思维导图的方式梳理知识点&am…...
在Win 11下使用Visual Studio 2019和cygwin编译JBR(Java SDK 17)源码
很多文章介绍了JDK 8和JDK11源码在Linux编译,很少有人介绍了JDK 17在windows的编译过程,所以写了这篇文章,为什么选用JBR 17版本,因为JBR17 版本集成了HotSwapAgent功能,具体HotSwapAgent有什么用,请看我前…...

java基础学习 day51 (匿名内部类)
1. 什么是匿名内部类? 隐藏了名字的内部类,实际名字为:外部类名$序号可以写在成员位置,为没有名字的成员内部类也可以写在局部位置,为没有名字的局部内部类 2. 匿名内部类的格式? new 类名/接口名() { 重…...
Spring MVC程序开发(三大功能)
文章目录一、什么是Spring MVC?1.MVC定义2.MVC与Spring MVC的关系3.创建方式二、Spring MVC的核心功能1.连接功能浏览器获取前端接口和后端程序连接功能实现get和post的区别Spring Boot热部署2.获取参数(1)传递单个参数(2)传递对…...
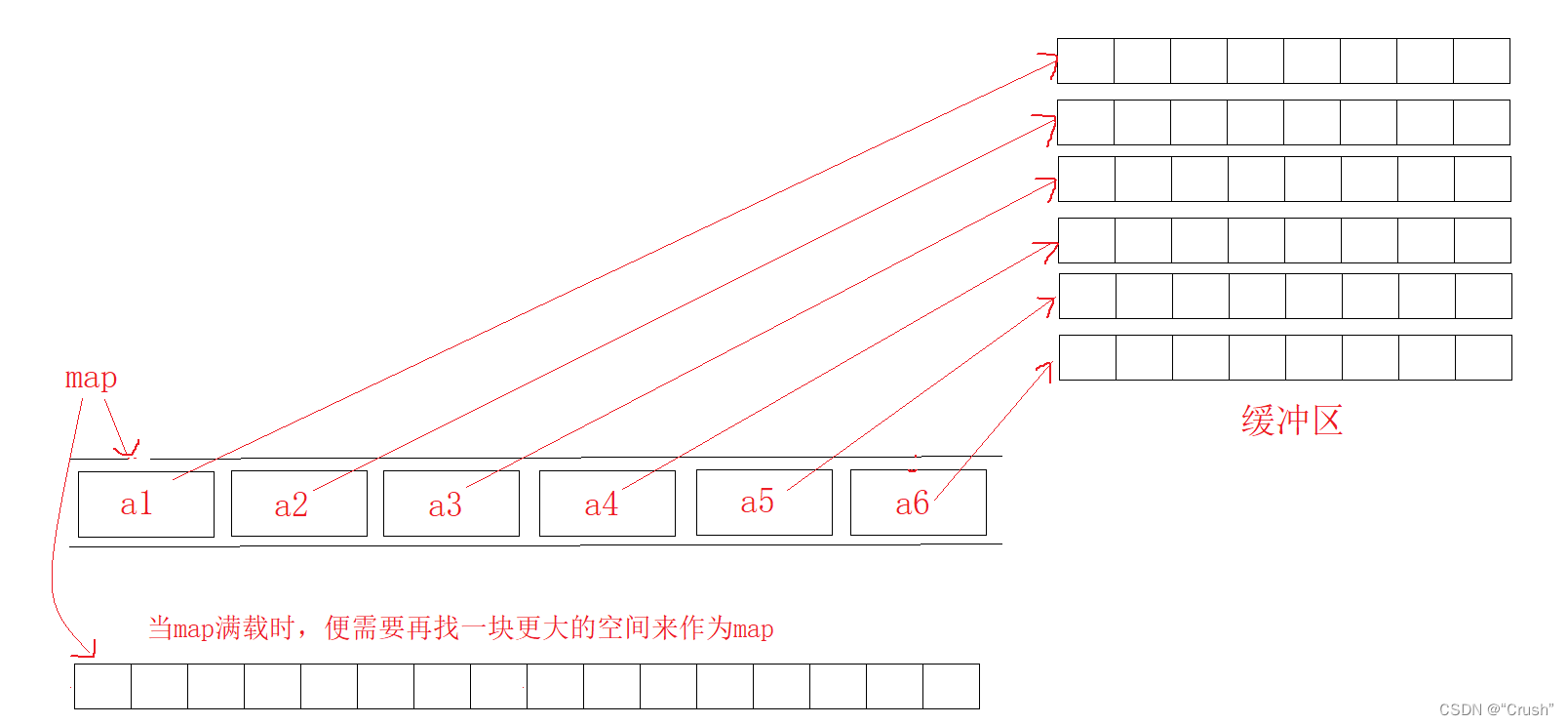
stack,queue
stack,queuestack的介绍和使用介绍使用模拟实现queue的介绍和使用介绍使用模拟实现priority_queue的介绍和使用介绍使用模拟实现容器适配器概念标准库中stack,queue的底层结构介绍deque原理缺陷deque作为stack,queue底层默认容器stack的介绍和使用 介绍 stack是适…...

shiro反序列化
shiro550反序列化 | 清风的博客这个看着更舒服点 环境搭建 JDK:1.7 Tomcat:8.5.83 shiro源码:下载地址:https://codeload.github.com/apache/shiro/zip/shiro-root-1.2.4 shiro war包:下载地址SHIRO-550/samples-…...
)
【GoF 23 概念理解】IoC/DI(控制反转/依赖注入)
搞清楚以下几个问题你就明白什么是 IoC/DI 了: 参与者都有谁?依赖:谁依赖于谁?为什么要依赖?注入:谁注入于谁?到底注入什么?控制反转:谁控制谁?控制什么&…...

stm32外设-GPIO
0. 写在最前 本栏目笔记都是基于stm32F10x 1. GPIO基本介绍 GPIO—general purpose intput output 是通用输入输出端口的简称,简单来说就是软件可控制的引脚, STM32芯片的GPIO引脚与外部设备连接起来,从而实现与外部通讯、控制以及数据采集的…...
AfxMessageBox 自定义封装
一般情况下AfxMessageBox是系统提供的一个对话框,若要做这种效果的,必须重写。 实例1: void test_SgxMemDialog_AutoSize() { //使用给定大小的对话框 CSgxMemDialog dlg(180, 60); dlg.SetWindowTitle(_T(" SegeX - CT&qu…...

登入vCenter显示503,证书过期解决办法
登入vCenter显示503 原因:当安全令牌服务 (STS) 证书已过期时,会出现这些问题。这会导致内部服务和解决方案用户无法获取有效令牌,从而导致无法按预期运行(证书两年后就会过期)。 解决办法&…...
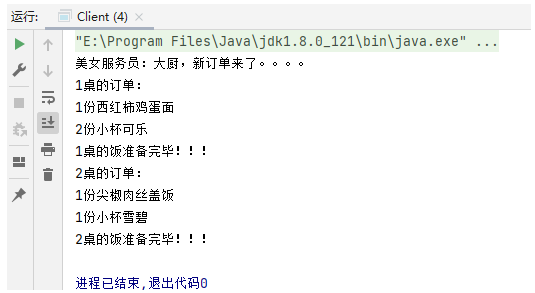
设计模式(十九)----行为型模式之命令模式
1、概述 日常生活中,我们出去吃饭都会遇到下面的场景。 定义: 将一个请求封装为一个对象,使发出请求的责任和执行请求的责任分割开。这样两者之间通过命令对象进行沟通,这样方便将命令对象进行存储、传递、调用、增加与管理。命…...
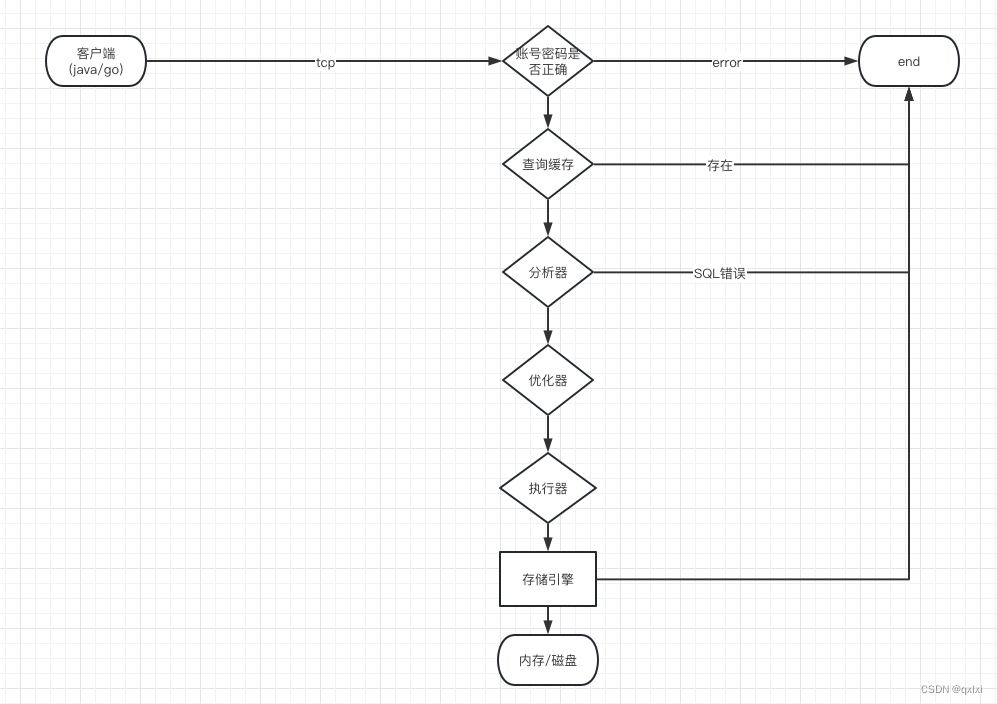
【数据库】数据库基础架构
数据库架构 数据库对于后端程序员来说是每天都需要打交道的系统,因此了解并掌握MySQL底层原理是必须的。 基础架构图 MySQL内部分为两层,一个是Server层,另一个是存储引擎层,而我们常用的就是MyISAM、InnoDB,主要负…...

English Learning - L2 语音作业打卡 双元音 [ɔɪ] [ɪə] Day16 2023.3.8 周三
English Learning - L2 语音作业打卡 双元音 [ɔɪ] [ɪə] Day16 2023.3.8 周三💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [ɔ…...

C++语法规则4(C++面向对象)
接口(抽象类) 接口描述了类的行为和功能,而不需要完成类的特定实现。C 接口是使用抽象类来实现的,抽象类与数据抽象互不混淆,数据抽象是一个把实现细节与相关的数据分离开的概念。 如果类中至少有一个函数被声明为纯虚…...

【Spring 深入学习】AOP的前世今生之后续
AOP的前世今生之后续 1. 概述 上篇文章【Spring 深入学习】AOP的前世今生之代理模式我们讲述了代理模式。而我们今天的主人公AOP就是基于代理模式实现的,所以我们今天会简单学习下AOP 2. 什么是AOP 是面向切面编程,一般可以帮助我们在不修改现有代码的情…...

软考高项——配置管理
配置管理配置管理配置管理6个主要活动配置项配置基线配置项的状态配置库配置库权限管理配置审计配置管理 配置管理的总线索包括: 1)配置管理6个主要活动 2)配置项 3)配置基线 4)配置项的状态 5)配置库 6&a…...

网站SEO优化,网站TDK三大标签SEO优化,LOGO SEO优化
SEO(Search Engine Optimization)汉译为搜索引擎优化,是一种利用搜索引擎的规则提高网站在有关搜索 引擎内自然排名的方式。 SEO 的目的是对网站进行深度的优化,从而帮助网站获取免费的流量,进而在搜索引擎上提升网站的…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...
