【抽代复习笔记】24-群(十八):循环群的两道例题
例1:证明:
(1)三次交错群A3是循环群,它与(Z3,+)同构,其中Z3 = {[0],[1],[2]};
(2)G = {1,i,-1,-i},G上的代数运算是数的乘法,则G是一个循环群,它同构于(Z4,+),其中Z4 = {[0],[1],[2],[3]}。
证:(1)A3 = {(1),(123),(132)},由于(123)^1 = (123),(123)^2 = (132),(123)^3 = (1),
所以A3中所有元素均可以由(123)生成,因此A3是一个循环群,且(123)是其生成元,即A3 = ((123)),
定义映射f:A3→Z3为f((123)^k) = [k],易证f是一个同构映射:
①对任意的(123)^k∈A3,存在[k]∈Z3与之对应,因此f是一个映射;
②对任意的[k]∈Z3,存在(123)^k∈A3与之对应,因此f是一个满射;
③由f((123)^k) = f((123)^h),可得出[k] = [h],从而(123)^k = (123)^h,因为假若(123)^k ≠ (123)^h,则(123)^(k-h) ≠ (123)^(h-h) = (1),这样[k]-[h] = [k-h]=f((123)^(k-h)) ≠ f((123)^(h-h)) = [h-h] = [0],即[k] - [h] ≠ [0],即[k] ≠ [h]+[0] = [h],这与前提条件矛盾,所以(123)^k = (123)^h,
因此f是一个单射;
④f((123)^k o (123)^h) = f((123)^(k+h)) = [k+h] = [k]+[h] = f((123)^k) + f((123)^h),因此f是一个同态映射。
综上所述,f是从A3→Z3的一个同构映射,从而(A3,o) ≅ (Z3,+)。
(2)因为i^1 = i,i^2 = -1,i^3 = -i,i^4 = 1,所以G中所有的元素都可以由其中的i生成,因此G是一个循环群,i是其生成元,即G = (i),
定义映射g:G→Z4为g(i^k) = [k],按照和(1)中同样的步骤,可以证明g是一个同构映射,
从而(G,×) ≅ (Z4,+)。
例2:求Z2,Z3,Z4,...,Z8中各元素的阶,并找出它们所有的生成元。
解:①Z2 = {[0],[1]},其中[0]是单位元,[0]^1 = [0],[1]^2 = [1]+[1] = [2] = [0],所以|[0]| = 1,|[1]| = 2,元素[0]和[1]均可以由[1]生成,所以[1]是生成元;
②Z3 = {[0],[1],[2]},其中[0]是单位元,[0]^1 = [0],[1]^3 = [1]+[1]+[1] = [3] = [0],[2]^3 = [6] = [0],所以|[0]| = 1,|[1]| = 2,|[2]| = 3,所有元素均可以由[1]或[2]生成,所以[1]、[2]是生成元;
③Z4 = {[0],[1],[2],[3]},|[0]| = 1,|[1]| = 4,|[2]| = 2,|[3]| = 4,[1],[2],[3]均是其生成元;
④Z5 = {[0],[1],[2],[3],[4]},|[0]| = 1,|[1]| = 5,|[2]| = 5,|[3]| = 5,|[4]| = 5,[1],[2],[3],[4]均是其生成元;
⑤Z6 = {[0],[1],[2],[3],[4],[5]},|[0]| = 1,|[1]| = 6,|[2]| = 3,|[3]| = 2,|[4]| = 3,|5| = 6,[1],[2],[3],[4],[5]均是其生成元;
⑥Z7 = {[0],[1],[2],[3],[4],[5],[6]},|[0]| = 1,|[1]| = 7,|[2]| = 7,|[3]| = 7,|[4]| = 7,|[5]| = 7,[1],[2],[3],[4],[5],[6]均是其生成元;
⑦Z8 = {[0],[1],[2],[3],[4],[5],[6],[7]},|[0]| = 1,|[1]| = 8,|[2]| = 4,|[3]| = 8,|[4]| = 2,|[5]| = 8,[1],[2],[3],[4],[5],[6],[7]均是其生成元;
(待续……)
相关文章:
:循环群的两道例题)
【抽代复习笔记】24-群(十八):循环群的两道例题
例1:证明: (1)三次交错群A3是循环群,它与(Z3,)同构,其中Z3 {[0],[1],[2]}; (2)G {1,i,-1,-i},G上的代数运算是数的乘法,则G是一个循环群&…...

Linux常见操作问题
1、登录刚创建的用户,无法操作。 注:etc/passwd文件是Linux操作系统中存储用户账户信息的文本文件,包含了系统中所有用户的基本信息,比如用户名、用户ID、用户组ID、用户家目录路径。 注:etc: 这个目录存放所有的系统…...

鲁工小装载机-前后桥传动轴油封更换记录
鲁工装载机 因前后桥大量漏齿轮油,故拆开查看、更换油封 一: 如图圈起来的地方是螺丝和钢板相别,用200的焊接电流用电焊机点开一个豁口后拆除螺丝。 转轴是拆除传动轴后的样子。 这就是拆下来的样子,这玩意插上边那图&…...

商城自动化测试实战 —— 登录+滑块验证
hello大家好,我是你们的小编! 本商城测试项目采取PO模型和数据分离式架构,采用pytestseleniumjenkins结合的方式进行脚本编写与运行,项目架构如下: 1、创建项目名称:code_shopping,创建所需项目…...

8.计算机视觉—增广和迁移
目录 1.数据增广数据增强数据增强的操作代码实现2.微调 迁移学习 Transfer learning(重要的技术)网络结构微调:当目标数据集比源数据集小得多时,微调有助于提高模型的泛化能力。训练固定一些层总结代码实现1.数据增广 CES上的真实故事 有一家做智能售货机的公司,发现他们…...

【Matlab】-- BP反向传播算法
文章目录 文章目录 00 写在前面01 BP算法介绍02 基于Matlab的BP算法03 代码解释 00 写在前面 BP算法可以结合鲸鱼算法、飞蛾扑火算法、粒子群算法、灰狼算法、蝙蝠算法等等各种优化算法一起,进行回归预测或者分类预测。 01 BP算法介绍 BP(Backpropag…...

【Python】 数据分析中的常见统计量:众数
那年夏天我和你躲在 这一大片宁静的海 直到后来我们都还在 对这个世界充满期待 今年冬天你已经不在 我的心空出了一块 很高兴遇见你 让我终究明白 回忆比真实精彩 🎵 王心凌《那年夏天宁静的海》 众数(Mode)是统计学中另…...

Karabiner-Elements 设置mac键盘
软件下载地址: Karabiner-Elements 修改键盘位置,但是重启后,就消失了。 {"description": "New Rule (change left_shiftcaps_lock to page_down, right_shiftcaps_lock to left_commandmission_control)","manip…...

Mybatis实现流程
一,UserDAO 接口定义 首先,定义 UserDAO接口,包含 getList()方法,定义类型为List<User>: package dao;import model.User; import java.util.List;public interface UserDAO {List<User> getList(); }二,…...
)
简单的springboot整合activiti5-serviceImpl部分(1)
简单的springboot整合activiti5.22.0-serviceImpl部分(1) 原来的流程serviceImpl部分代码过多,所以此处单独记录一下,此处记录的是serviceImpl第一部分代码 package cn.git.workflow.service.impl;import cn.git.cache.api.BaseCacheApi; import cn.gi…...

snat、dnat和firewalld
目录 概述 SNAT源地址转换 DANT目的地址转换 抓包 firewalld 端口管理 概述 snat :源地址转换 内网——外网 内网ip转换成可以访问外网的ip 也就是内网的多个主机可以只有一个有效的公网ip地址访问外部网络 DNAT:目的地址转发 外部用户&#…...

[数据集][目标检测]鸡蛋缺陷检测数据集VOC+YOLO格式2918张2类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):2918 标注数量(xml文件个数):2918 标注数量(txt文件个数):2918 标注…...

前后端防重复提交
数据重复提交是一个大忌,会带来无效数据,应该在前端和后端都建议检测防范。 前端一般是按钮按下触发数据提交,如果用户鼠标操作习惯不好,或者鼠标或系统设置问题会导致鼠标连击,如果前端不做相关处理,可能会…...
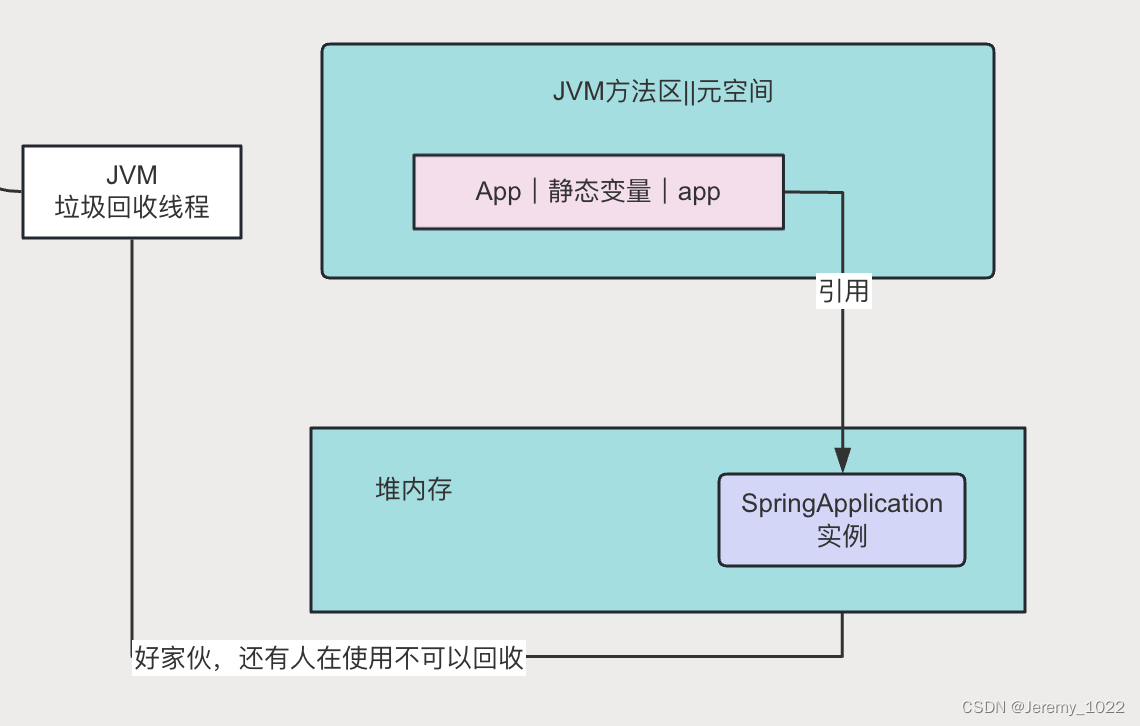
JVM专题八:JVM如何判断可回收对象
在JVM专题七:JVM垃圾回收机制中提到JVM的垃圾回收机制是一个自动化的后台进程,它通过周期性地检查和回收不可达的对象(垃圾),帮助管理内存资源,确保应用程序的高效运行。今天就让我们来看看JVM到底是怎么定…...

binary_cross_entropy_with_logits函数的参数设定
binary_cross_entropy_with_logits 该函数参数: logits (Tensor) - 输入预测值。其数据类型为float16或float32。 label (Tensor) - 输入目标值,shape与 logits 相同。数据类型为float16或float32。 weight (Tensor,可选) - 指定每个批次二…...

Python 面试【★★★★★】
欢迎莅临我的博客 💝💝💝,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...

C# StringBuilder
以下是一些基本的 StringBuilder 使用方法:创建 StringBuilder 实例:追加字符串:插入字符串:删除字符串:替换字符串:清空 StringBuilder:转换 StringBuilder 为字符串:使用容量&…...
4个文章生成器免费版分享,让文章创作更轻松便捷
在当今这个信息飞速传播的时代,文章创作的重要性愈发凸显。无论是从事内容创作的专业人士,还是偶尔需要撰写文章的普通大众,都希望能更高效地完成文章创作任务。而在实际操作中,我们常常会遇到思路卡顿、没有创作灵感的问题。今天…...

redis-cluster(集群模式搭建)
redis中间件版本: redis-5.0.5环境介绍 这里使用服务器数量3,分别为172.0.0.1,172.0.0.2,172.0.0.3,每台机器redis节点数量2个,共6个redis节点构成redis-cluster模式。编译安装包 在172.0.0.1的机器上进入安装目录 cd …...

使用vite官网和vue3官网分别都可以创建vue3项目
问: npm init vitelatest 和 npm create vuelatest创建的vue3项目有什么区别? 回答: npm init vitelatest 和 npm create vuelatest 分别是使用 Vite 和 Vue CLI 工具创建 Vue 项目的两种方式,它们之间有几个主要区别: 1. **构建工具:** …...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
