复分析——第9章——椭圆函数导论(E.M. Stein R. Shakarchi)
第 9 章 椭圆函数导论
(An Introduction to Elliptic Functions)
The form that Jacobi had given to the theory of elliptic
functions was far from perfection; its flaws are obvious.
At the base we find three fundamental functions sn,
cn and dn. These functions do not have the same
periods...
In Weierstrass’ system, instead of three fundamental
functions, there is only one, ℘(u), and it is the
simplest of all having the same periods. It has only
one double infinity; and finally its definition is so that
it does not change when one replaces one system of
periods by another equivalent system.
( Jacobi 给出的椭圆函数理论形式远非完美,其缺陷显而易见。在基础部分,我们发现三个基本函数 sn、cn 和 dn。这些函数的周期并不相同……
在 Weierstrass 的系统中,没有三个基本函数,只有一个,℘(u),它是所有具有相同周期的函数中最简单的一个。它只有一个双无穷大;最后,它的定义是,当用另一个等价系统替换一个周期系统时,它不会改变。)
-------------------------------------------------------------------------------------------------H. Poincaré,1899
椭圆函数理论最初源于对椭圆积分的研究,它在数学的多个领域都受到广泛关注。通常,那些积分可以被描述为形如 和形式。其中 R 是比率函数(rational function),P 是三次或四次多项式(注:P 为二次多项式的情况在本质上是“圆函数(circular functions)”,可以简化为三角函数
、
等)。 这些积分用于计算椭圆或双纽线(lemniscate)的弧长,以及各种其他问题。它们的早期研究集中在其特殊的变换性质和固有双周期性的发现上。我们在上一章第 4.5 节中讨论的半平面到矩形的映射函数中看到了后一种现象的一个例子。
正是 Jacobi 通过系统地研究双周期函数(称为椭圆函数)改变了这一主题。在这个理论中,他引入的 θ 函数(theta functions)起着决定性的作用。在他之后,Weierstrass发展了另一种方法,这种方法在初始阶段更简单、更优雅。它基于他的 ℘ 函数(译注:符号 ℘ 称为 weierstrass p ,其 Unicode为 “02118” , LaTex语法为“\wp”),在本章中,我们将概述该理论的发端。我们将通过考虑 Eisenstein 级数及其涉及除数函数的表达式,尽可能地瞥见与数论的可能联系。θ 函数与组合学(combinatorics)和数论有许多更直接的联系,我们将在下一章中讨论。我们将在那里看到的显著事实证明了这些函数在数学中具有极大的影响(interest)。因此,它们应该会弱化上面关于 Jacobi 理论不完善的严厉意见。
1. 椭圆函数(Elliptic functions)
我们感兴趣的是在 ℂ 上具有两个周期的亚纯函数 f ;即,存在两个非零复数 和
使得
和
(对于任意 z∈ℂ )。
我们称具有两个周期的函数为双周期函数(doubly periodic functions)。当 和
在 ℝ 上是线性相关(即
) 时的这种情况我们是不感兴趣的。事实上,练习 1 表明,在这种情况下,f 要么是具有简单周期的同期函数(若商
是比率的),要么 f 是一个常量(若商
是非比率的)。因此,我们做以下假设:
和
在 ℝ 上是线性无关的。
我们现在描述一种将在本章中广泛使用的规范化方法(normalization)。令 。由于 𝝉 和 1/𝝉 具有相反符号的虚部,且因为 𝝉 不是实数,故我们可以假设(在可能的交换
和
的角色之后)Im(𝝉) > 0 。现在注意到,对于函数 f ,当且仅当函数
具有周期 1 和 𝝉 时,其才具有周期
和
,此外,当且仅当 F 是亚纯函数时,f 是亚纯函数。再者,f 的属性直接推导于 F 。因此,我们可以不失一般性地假设,f 是在 ℂ 上具有周期 1 和 𝝉 的亚纯函数(其中,Im(𝝉) > 0 )。
连续应用周期性条件可得出
(1) f (z + n + m 𝝉) = f (z) (对于任意整数 n ,m 和任意 z∈ℂ ),
因此,很自然地考虑定义为
的 ℂ 中的晶格(lattice,或称格点)。
我们称 1 和 𝝉 生成(generate) Λ (见图 1 )。
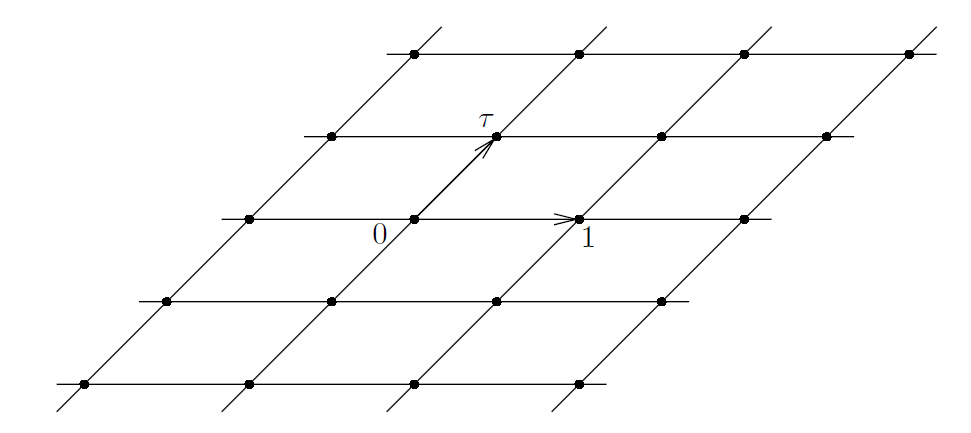
------------------------------------------图1: 由 1 和 𝝉 生成格式 Λ -----------------------------------------------------
等式(1)指的是,f 在按 Λ 的元素的平移下是常量。与晶格 Λ 相关的是定义为
。
的基础平行四边形(fundamental parallelogram)。
基本平行四边的重要性源于 f 完全确定于其在 上的行为这个事实。为了理解这一点,我们需要一个定义:对于两个复数 z 和 w ,若
(对于某些 n ,m ∈ℤ ),
则称这两个复数是模 Λ 同余的(congruent mudulo Λ),我们记为 z ~ w 。换句话说,z 和 w 在晶格中相差一个点,即 z - w ∈Λ 。根据(1)我们推断出,只要 z ~ w ,则 f (z) = f(w) 。若我们可以证明,z∈ℂ 中的任意点与 中的一个唯一点是同余的,则我们将完成证明 f 完全由其在基本科行四边形中的值确定。假设已知 z = x + iy ,并记为 z = a + bτ (其中,a ,b ∈ℝ ))。这是合理的,因为 1 和 𝝉 构成了二维向量空间 ℂ 的实数(reals)之上的一个基底(basis)。然后,分别选择 ≤ a 和 ≤ b 的最大整数 n 和 m 。若我们令 w = z - n – mτ ,则根据定义有 z ~ w ,此外,w = (a - n) + (b - m) 𝝉。根据构造,显然
。为了证明唯一性,假设
和
是
中的两个同余的点。若我们记为 w = a + bτ 和
,则
,因此
和
均为整数。但是由于
, 我们有
,则这意味着
。类似地,
,从而我们推导出
。
更一般地,一个周期平行四边形 P 是基础平行四边形的任意平移,即 (见图 2 ) 。
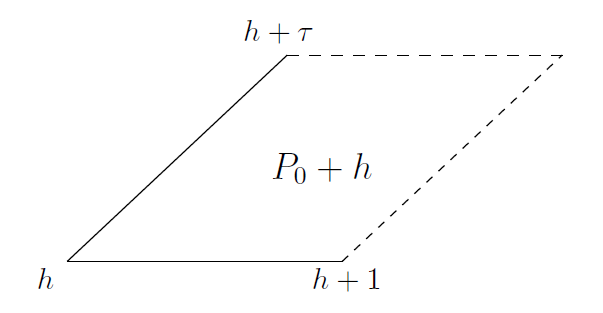
-----------------------------------------------------图 2: 一个周期平行四边形------------------------------------------
由于我们可以应用引理于 z - h ,我们推断出 ℂ 中的每一个点都与已知周期平行四边形中的唯一点同余。因此,f 由其在任何周期平行四边形上的行为唯一决定。
最后,注意到 和
导致(give rise to)复平面
的覆盖(covering)(或平铺(tiling)),此外,这个并集是不相交的。从我们刚刚收集的事实和 的定义可以立即得出这个结论。我们总结一下迄今为止所看到的内容。
命题 1.1 假设 f 是一个具有两个生成晶格 Λ 的周期 1 和 𝝉 的亚纯函数。则:
( i ) ℂ 中的每一个点都与基础平行四边行中的一个唯一点同余。
( ii ) ℂ 中的每一个点都与任意已知的周期平行四边行中的一个唯一点同余。
( iii ) 晶格 Λ 在(2)的意义上提供了复平面的一个不相交的覆盖。
( iv ) 函数 f 完全确定于其在任何周期平行四边形中的值。
1.1 Liouville定理(Liouville’s theorems)
现在我们可以明白为什么我们从一开始就假设 f 是亚纯的而不是全纯的。
定理 1.2 复可积的双周期函数是常量。
证明:
函数完全由其在 上的值确定,因为
的闭包是紧的,我们推断出函数在 ℂ 上有界。因此,根据第 2 章中给出的 Liouville 定理,函数是常量。非常量双周期亚纯函数被称为随圆函数(elliptic function)。由于亚纯函数在任何大圆盘上只能有有限多个零点和极点,因此我们看到椭圆函数在任何已知周期平行四边形中也只能有有限多个零点和极点,尤其是在基础平行四边形中。当然,不能排除 f 在
的边界上有一个极点或零点。
像往常一样,我们用重数(multiplicity)计算极点和零点。记住这一点,我们可以证明以下定理。
定理 1.3 一个椭圆函数在 中的极点总数总是 ≥ 2 。
换句话说,f 不会只有一个简单极点。它一定至少有两个极点,并且这不能排除重数 ≥ 2 的单极点的情况。
证明:
首先假设 f 在基础平行四边形在边界 上没有极点。根据留数定理,我们有
,
我们推断出积分是 0 。为了理解这一点,我们简单地应用 f 的周期性。注意到
,
且对边的积分相消。例如
。
对于其它成对的边也类似。因此, 且
。因此,f 在
中一定至少有两个极点。
若 f 在 上有一个极点,选择一个小的 h∈ℂ 使得
,则 f 在 ∂P 上没有极点。如前论证,我们求得 f 在 P 中一下至少有两个极点,且因为同样的结论对于
也成立。
椭圆函数的极点总数(按其重数计算)称为其阶(order)。下一个定理说,如果零点按其重数计算,则椭圆函数的零点数与极点数一样多。
定理 1.4 每一个 m 阶椭圆函数在 中都有 m 个零点。
证明:
首先假设 f 在 和边界上没有零点或极点,我们知道,通过第 3 章中的幅角原理(argument principle),有
,
(译注:符号 𝖟 是字母 z 的德文尖角体,符号 𝖕 是字母 p 的德文尖角体)
其中, 和
分别表示
中 f 的零点和极点数。根据周期性,我们可以按前面定理的证明那样论证,以求得
,因此,
。
在当 f 的零点或极点位于 上的时候的这种情况下,只需将幅角原理应用到 P 的平移上即可。
因此,若 f 是一个椭圆,则方程 f (z) = c 具有与 f 的阶相同数量的解(对于每一个 c∈ℂ),只因为 f – c 是椭圆,并且具有与 f 同样多的极点。
尽管上述定理相当简单,但仍存在证明椭圆函数存在的问题。现在我们来谈谈这个问题的建设性解决方案。
1.2 Weierstrass ℘ 函数(The Weierstrass ℘ function)
1.2.1 2阶椭圆函数(An elliptic function of order two)
本节专门介绍椭圆函数的基本例子。如上所示,任何椭圆函数都一定至少有两个极点;事实上,我们将构造一个椭圆函数,其唯一奇点将是周期生成的晶格上的双极点。
在研究双周期函数的情况之前,让我们首先简要考虑只有一个周期的函数。如果想要构造一个周期为 1 且极点位于所有整数处的函数,一个简单的选择是求和
。
注意,若我们用 (z + 1) 替换 z ,这个和保持不变,且极点位于整数处。然而,定义 F的这个级数不是绝对收敛的。为了补救(remedy)这个问题,我们按对称求和,即,我们定义
。
在最右侧,我们已经配对了(paired up)对应的 n 和 –n 项,这是一种技巧,使得方括号中的量 译注:表示右侧以
界),因此,最后的和是绝对收敛的。因而,F 是亚纯的且极点恰好位于整数处。事实上,我们在前面的第 5 章中已经证明
。
存在第二种处理级数 的方式, 将其记为
,
其中,求和是在所有非零整数上进行的。注意到, ,这使得这个级数绝对收敛。此外,由于
,
我们得到与使用前面的方法而得到和相同。
与此类似,我们的想法是模仿(mimic)上面的内容来产生我们的第一个椭圆函数的例子。我们想将其写成
,
但这个级数同样不是绝对收敛的。有几种方法可以尝试理解这个级数(参见问题 1 ),但最简单的方法是遵循我们处理余切级数的第二种方法。
为了克服这个级数的非绝对收敛性,我们令 表示晶格减去原点,即
,我们转而考虑以下级数:
,
其中,我们已经减去了因子 以使得和式收敛。现在,方括号中的项是
(当 |ω|⟶ ∞ 时),
一旦我们证明了以下引理,新的级数将定义一个具有所需极点的亚纯函数。
引理 1.5 两个级数
和
(若 r > 2)
收敛。
回顾一下,根据第 7 章末尾的评注,二重级数是否绝对收敛的问题与求和的顺序无关。在本例中,我们首先对 m 求和,然后对 n 求和。
对于第一个级数,可以应用通常的积分比较(注:当 k – 1 ≤ x ≤ k 时 ,我们简单地使用 ;此外,可参见第 I 册第 8 章中的第一个图)。对于每一个 n ≠ 0 ,有
。
因此,r > 2 意味着
。
为了证明第二个级数也是收敛的,只需证明存在一个常量 c 使得
|n| + |m| ≤ c| n + 𝒯m | (对于任意 n,m∈ℤ)
即可。若存在一个正常量 a 使得 x ≤ ay, 则我们记为 x ≲ y (译注:符号 的 Unicode 码是“02272”,LaTex语法是“\lesssim”,读作“小于相似”)。此外,若 x ≲ y 和 y ≲ x 均成立,我们记为 x ≈ y 。注意到,对于任意两个正常量 A 和 B ,我们有
。
在一方面, 且
,因此
。在另一方面,只需对两侧进行平方便可得到
。
现在,引理 1.5 中第二个级数收敛的证明是通过以下观察而得出的结果:
|n| + |m| ≈ | n + m𝒯 | ( 只要 𝒯∈ℍ) 。
事实上,若 𝒯 = s + it (s , t∈ℍ 且 t > 0),则根据前面的观察,我们有
。
从而,通过分别考虑|n| ≤ 2|ms|和 |n| ≥ 2|ms|这两种情况,我们得到 |n + ms| + |m| ≈ |n| + |m|。
评注:
上述证明表明,当 r > 2 时, 在每一个半平面 Im(𝒯)≥ δ > 0 中一致收敛。对比而方,当 r = 2 时,这个级数不收敛(练习 3 )。有了这个技术点,我们现在可以回到 Weierstrass ℘ 函数的定义, 其由级数
。(译注:符号“℘ ”是Weierstrass p 。)
我们断言,℘ 是一个在晶格上具有双极点的亚纯函数。为了理解这一点,假设 |z| < R ,并写成
。
第二项和中的项对于|z| < R 是一致地 的,因此,根据引理 1.5 这第二项和在域 |z| < R 内定义了一个全纯函数。最后,请注意第一项和在圆盘 |z| < R 中的格点(lattice points)上呈现双极点。
注意,由于插入了 这一项,是否 ℘ 是双周期已不太明显。然而,这是事实,且 ℘ 具有 2 阶椭圆函数所具有的所有属性。我们在下面定理中汇聚这些结论。
定理 1.6 函数 ℘ 是一个随圆函数且具有周期 1 和 𝒯 ,并且在格点上具有双极点。
证明:
现在只需证明 ℘ 是一个具有正确周期的周期函数即可。为此,注意到,对 ℘ 的级数逐项微分便给出了其导数,因此
。
这对我们来说完成了两件事情。第一,只要 z 不是格点,则微分级数一致收敛,属于引理 1.5 的 r = 3 这种情况。第二,微分也消除了减去项 ;因此,
这个级数显然是双周期函数,且以 1 和 𝒯 为周期,因为用 z + 1 和 z + 𝒯 替换 z 和,其值保持不变。
因此,存在两个常量 a 和 b 使得
℘( z + 1) = ℘(z) + a 和 ℘(z + 𝒯 ) = ℘(z) + b 。
然而,很明显的是,根据定义,℘ 是偶函数,即 ℘( z ) = ℘(-z) , 因为 ω∈Λ 上的和可以被 -ω∈Λ 上的和替代。因此,有 ℘( -1/2) = ℘(1/2)和 ℘( - 𝒯/2) = ℘( 𝒯/2) ,分别令 z = -1/2 和 z = - 𝒯/2 ,则在上述两个表达式中证明了 a = b = 0 。
可以不用微分而直接给出 ℘ 周期性的证明;见练习 4 。
1.2.2 ℘ 的属性(Properties of ℘ )
按顺序作几条评论。首先,我们已经注意到,℘ 是偶函数,因此, 是奇函数。由于
也是以 1 和 𝒯 为周期的周期函数,我们求得
。
事实上,我们有(例如)
。
由于 是椭圆函数且阶为 3 ,这三个点 1/2,𝒯/2 ,和(1 + 𝒯 )/2(被称为半周期(half periods))是
在基础平行四边形中的唯一根,他们的重数均为 1 。因此,若我们定义
,
, 和
,
我们推断出方程 在 1/2 处具有一个双根。由于 ℘ 的阶为 2,方程
在平行四边形中不存在其它的解。类似地,方程
和
分别在 𝒯/2 和 (1 + 𝒯 )/2 处具有唯一的双根。特别是,这三个数
,
和
是不同的,否则,℘ 在基础平行四边形中至少会有四个根,这与 ℘ 的阶为 2 相矛盾。从这些观察出发,我们可以证明下面的定理。
定理 1.7 函数 在 ℘ 中是三次多项式
。
证明:
在基础平行四边形中的唯一根具重数 2,位于点 1/2,𝒯/2 ,和(1 + 𝒯 )/2 处。此外,
在这些点处有双根。而且,F 在格点处具有 6 阶极点,因此,
也是如此(因为
在那些点处具有 3 阶极点)。继而,
是全纯的且仍具有双周期,因此,这个商是常量。为了求得这个常量的值,我们注意到 0 附近的 z ,我们有
和
,
其中,省略点(...) 表示更高阶项。因此,这个常量是 4 , 从而定理得证。
接下来,我们通过证明每一个椭圆函数都是 ℘ 和 的简单组合,从而证明 ℘ 函数的普遍性。
定理 1.8 每一个具有周期 1 和 𝒯 的椭圆函数都是 ℘ 和 的比率函数(rational function)。
该定理将是其以下版本的简单推论。
引理 1.9 每一个具有周期 1 和 𝒯 的偶椭圆函数 F 都是 ℘ 的比率函数。
证明:
若 F 在原点有零点或极点,则它一定是偶数阶,因为 F 是偶函数。因此,存在一个 整数 m ,使得 在格点具有零点或极点。故而我们可以假设 F 本身在 Λ 具有零点或极点。
我们的即刻目标就是要用 ℘ 来构造一个与 F 具有相同的零点和极点的双周期函数 G 。为了实现这一点,我们回顾一下,℘( z) - ℘( a) 具有一个 2 阶单零点(若 a 是一个半周期),否则,函数在 a 和 – a 有两个不同的零点。因此,我们必须存细地计数 F的零点和极点。
若 a 是 F 的一个零点,则 –a 也是,因为 F 是偶函数。 此外,当且仅当 F 的周期是半周期时,a 和 – a 同余,在这种情况下零点是偶数阶。因此,若按重数计算的点 描述了 F 的所有零点,则
的根恰好与 F 的根相同。同样,类似的论证(其中, (具有重数)(注:若
不是半周期,则
和
在这些点具有与 F 相同的重数。若
是半周期,则
和
是同余的,则每一个都具有 F 在那些点的重数的一半))则可以证明
是周期函数,且具有与 F 相同的零点和极点。因此 F/G 是全纯的且为双周期,故而是常量。这就推断出对引理的证明。
为了证明定理,我们首先回顾到,℘ 是偶函数而 是奇函数。然后,我们将 f 写成一个偶函数与一个奇函数之和,即
,
其中, 和
。则,由于
是偶函数,将引理应用于
和
, 很显然可以得到 f 是 ℘ 和
的比率函数。
2. 椭圆函数模特性和Eisenstein[áizəntʃain]级数(The modular character of elliptic functions and Eisenstein series)
现在我们研究椭圆函数的模数特性,即它们基于 𝒯 的依赖性。回想一下我们在本章开头所做的标准化。我们从两个在 ℝ 上线性无关的周期 和
开始,且我们定义
。然后,我们可以假设 Im( 𝒯 ) > 0 ,此外,并假设这两个周期是 1 和 𝒯 。接下来,我们考虑由 1 和 𝒯 所生成的晶格并构造函数 ℘ (具有周期 1 和 𝒯 的 2 阶椭圆函数)。由于对 ℘ 的构造取决于 𝒯 ,因此我们可以写成
以代替 ℘ 。这导致我们改变观点,并主要将
视为 𝒯 的函数。这种方法产生了很多有趣的新见解。我们考量由以下观察引导。首先,由于 1 和 𝒯 生成了
的周期,而 1 和 𝒯 + 1 生成了同样的周期,我们可以预期
和
之间存在一种紧密的联系。事实上,容易看出它们是恒等的。第二,由于
,根据第 1 节开头施加的标准化,我们发现
。这实质上对应
和
的一个交换,因此,我们也可以预期
和
之间存在一种密切的关系。事实上,容易验证
。
因此,我们被导向去考虑上半平面 Im( 𝒯 ) > 0 的变换群(通过两个变换 𝒯 ⟼ 𝒯 + 1 和 𝒯 ⟼ -1/𝒯 而生成)。我们称这样的群为模群(modular group)。根据我们的说法,可以预期所有本质上附加到 的量都反映了上述变换。当我们考虑 Eisenstein[áizəntʃain](译注: Ferdinand Eisenstein,德国数学家,1823年4月16日-1852年10月11日) 级数时,我们就可以清楚地看到这一点。
2.1 Eisenstein级数(Eisenstein series)
k 阶 Eisenstein 级数被定义为
(只要 k 是≥ 3 的整数和 𝒯 是复数且 Im( 𝒯 ) > 0)。
若 Λ 是由 1 和 𝒯 所生成的晶格,且若我们写成 ω = n + m𝒯 ,则 Eisenstein 级数的另一种表达式是 。
定理 2.1 Eisenstein 级数具有下列属性:
( i ) 若 k ≥ 3 则级数 收敛,且在上半平面是全纯的。
( ii ) 若 k 是奇数则级数 。
( iii ) 满足下列变换关系:
和
。
这最后一个属性有时候被称为 Eisenstein 级数的模特征(modular character)。在下一节中,我们将会回到讨论这些特征及其它模恒等式。
证明:
根据引理 1.5 及其后的评注,级数 在每一个复平面 Im( 𝒯 ) ≥ δ > 0 中绝对且一致收敛(只要 k ≥ 3 );因此,
在上半平面 Im( 𝒯 ) > 0 中是全纯的。
根据对称性,用 –n 和 –m 替换 n 和 m ,我们可以看到,只要 k 是奇数,Eisenstein 级数恒为 0 。最后, 是以 1 为周期的周期函数是很显而易见的,从事实 n + m(𝒯 + 1) = n + m + m𝒯 以及通过用 n 替代 n + m 的方式重排和式可推导出结论。此外,我们有
,
再一次地,我们可以重排和式,这次用(n,m) 替换 (-m,n)。而结论(iii)则如下所述。
评注:
由于第二个属性的缘故,有些作者将 k 阶 Eisenstein 级数定义为 ,可能在其前面带一个常量因子。
当我们研究 ℘ 在 0 附近的级数展开式的时候, 与 Weierstrass ℘ 函数之间的联系就出现了。
定理 2.2 对于 0 附近的 z ,我们有
。
证明:
从 ℘ 的定义出发,若我们注意到我们可以用 –ω 替换掉 ω 而无需改变和式,则我们有
,
其中,ω = n + m 𝒯 。恒等式
(对于 |ω| < 1 )
(上式可从微分等比级数推导出)
意味着对于任意小的 z ,
。
因此,
,
其中,我们利用了 (只要 𝓁 是奇数)这个事实。
基于这个定理,我们获得了如下三个 z 在 0 附近的展开式:
,
,
。
从这些展开式出发,我们可以看到,差分函数 是 0 附近是全纯的,事实上,在原点处等于 0 。由于这个差分函数也是双周期的,根据定理 1.2 我们推断出它是常量,因此其恒等于 0 。这就证明了下列的推论。
推论 2.3 若 且
, 则
。
注意,这个恒等式是定理 1.7 的另一个版本,它允许我们用爱 Eisenstein 级数来表达 的对称函数。
2.2 Eisenstein级数和除数函数(Eisenstein series and divisor functions)
现在我们将描述 Eisenstein 级数和一些数论量(number-theoretic quantities)之间的联系。如果我们考虑周期函数 的 Fourier 展开式中的 Fourier 系数,就会出现这种关系。
按等价方式,我们可以写成 (
) ,并将 ℇ 的 Laurent 展开式作为 z 的函数研究。
我们从下面的引理开始。
引理 2.4 若 k ≥ 2 且 Im( 𝒯 ) > 0 ,则
。
证明:
应用 Poisson 求和公式到 可推出这个恒等式;见第 4 章练习 7 。
此引理的另一种证明是指出首先足以建立 k = 2 的公式,因为其他情况是通过逐项微分获得的。为了证明这种特殊情况,我们对第 5 章中导出的余切公式进行微分,即
。
由此得到
。
现在对正弦函数使用 Euler 公式, 并结合事实
,
即可求得预期的结果。
根据这个引理,我们可以在 Eisenstein 级数、ζ 函数和除数函数之间建立联系。这里出现的除数函数(divisor function) 定义为 r 的除数的 𝓁 次幂之后,即
。
定理 2.5 若 k ≥ 4 是偶数且 Im( 𝒯 ) > 0 ,则
。
证明:
首先注意到, 。若 Im( 𝒯 ) = t ,则只要
我们便有
,且通过将定理中的级数与
对比,我们可以看出,定理中的级数在任意
的半平面中是绝对收敛的。为了建立这个公式,我们使用 Ek
![]() 和 ζ 的定义,和 k 是偶数的事实,以及前面的引理(用 m𝒯 替代 𝒯 )而先后可得到
和 ζ 的定义,和 k 是偶数的事实,以及前面的引理(用 m𝒯 替代 𝒯 )而先后可得到
。
这就证明了预期的公式。
最后,我们回到被“禁止”的 k = 2 这种情况。我们脑海中的级数 不再绝对收敛,但无论如何,我们寻求给它赋予某种意义。我们定义
,
以指定的次序求和,且(n,m) ≠ (0,0)。上述定理给出的论证证明了二重求和收敛,且事实上具有预期的表达式。
推论 2.6 定义 F 的按指定次序求和的双重求和表达式收敛。我们有
,
其中, 是 r 的除数之和。
可以看出, 不等于 F( 𝒯 ) ,这等同于称,对于 F 的双重级数,当我们先按 m 再按 n 求和时,会得出不同的值(
,
的逆)。事实证明,尽管如此,被禁止的Eisenstein 级数(forbidden Eisenstein series) F( 𝒯 ) 仍然可以在证明有关将整数表示为四个平方和的著名定理中以至关重要的方式使用。我们将在下一章讨论这些问题。
内容来源:
<< Complex Analysis >> ,作者:E.M. Stein & R. Shakarchi
术语参考资料:
<<英汉数学词汇>>,张鸿林,葛显良 编订,清华大学比版社,2018年
<<新英汉数学词汇>> ,科学出版社名词室,科学出版社, 2002年
<<物理学名词>>,第三版,科学出版社会,2019年
<<英汉综合物理学词汇>> 科学出版社,1999年
相关文章:
复分析——第9章——椭圆函数导论(E.M. Stein R. Shakarchi)
第 9 章 椭圆函数导论 (An Introduction to Elliptic Functions) The form that Jacobi had given to the theory of elliptic functions was far from perfection; its flaws are obvious. At the base we find three fundamental functions sn, cn and dn. These functio…...

使用kubeadm安装k8s并部署应用
安装k8s 1. 准备机器 准备三台机器 192.168.136.104 master节点 192.168.136.105 worker节点 192.168.136.106 worker节点2. 安装前配置 1.基础环境 ######################################################################### #关闭防火墙: 如果是云服务器&…...
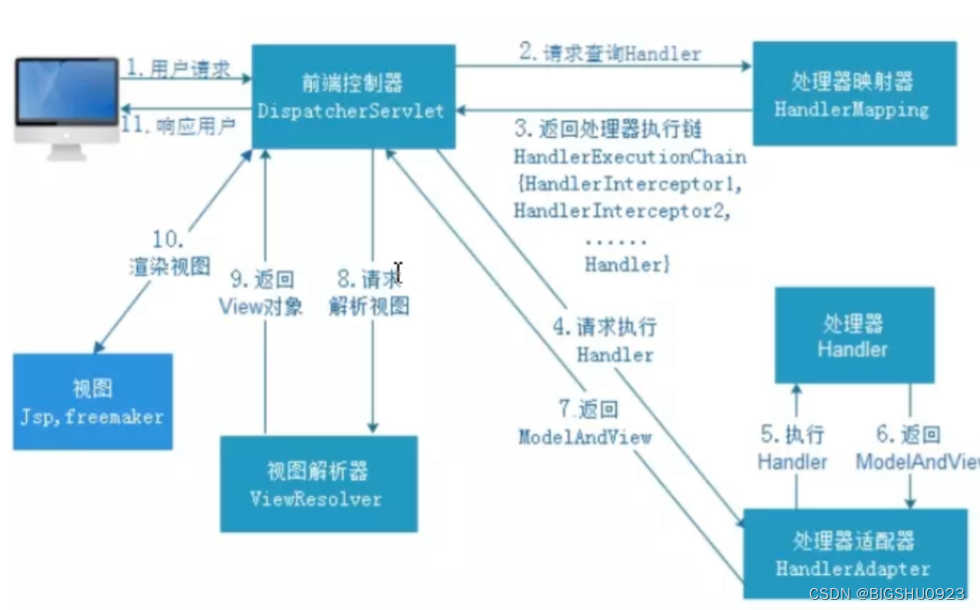
springMVC学习
概述 Spring MVC(Model-View-Controller,模型-视图-控制器)是Spring框架的一部分,用于构建基于Java的Web应用程序。它遵循MVC设计模式,分离了应用程序的不同方面(输入逻辑、业务逻辑和UI逻辑)&…...

深入探讨光刻技术:半导体制造的关键工艺
前言 光刻(Photolithography)是现代半导体制造过程中不可或缺的一环,它的精度和能力直接决定了芯片的性能和密度。本文将详细介绍光刻技术的基本原理、过程、关键技术及其在半导体制造中的重要性。 光刻技术的基本原理 光刻是一种利用光化…...
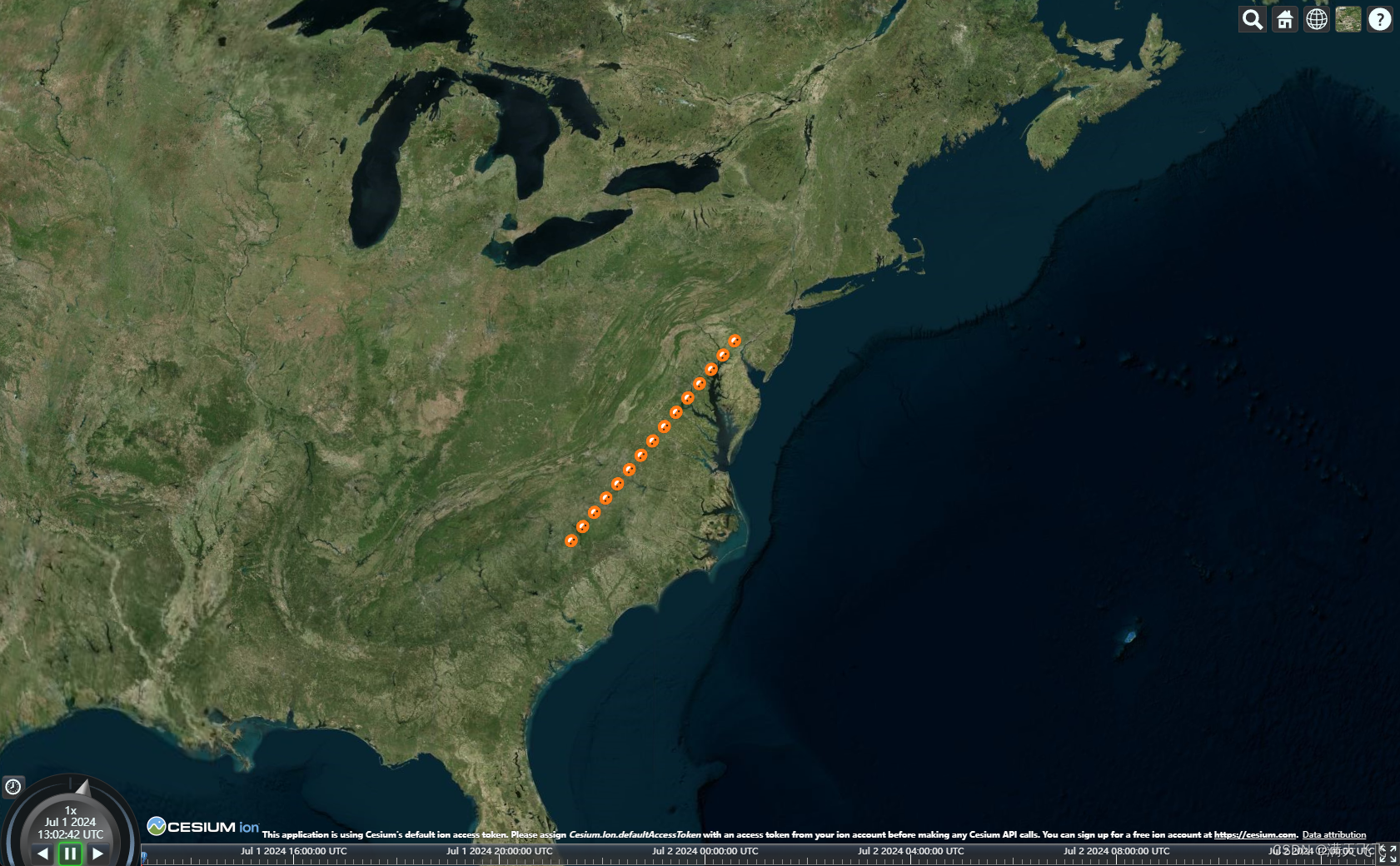
CesiumJS【Basic】- #042 绘制纹理线(Primitive方式)
文章目录 绘制纹理线(Primitive方式)1 目标2 代码2.1 main.ts3 资源文件绘制纹理线(Primitive方式) 1 目标 使用Primitive方式绘制纹理线 2 代码 2.1 main.ts var start = Cesium.Cartesian3.fromDegrees(-75.59777, 40.03883);var...

代码随想录第38天|动态规划
1049. 最后一块石头的重量 II 参考 备注: 当物体容量也等同于价值时, 01背包问题的含义则是利用好最大的背包容量sum/2, 使得结果尽可能的接近或者小于 sum/2 等价: 尽可能的平分成相同的两堆, 其差则为结果, 比如 (abc)-d, (ac)-(bd) , 最终的结果是一堆减去另外一堆的和, 问…...
java生成excel,uniapp微信小程序接收excel并打开
java引包,引的是apache.poi <dependency><groupId>org.apache.poi</groupId><artifactId>poi-ooxml</artifactId><version>5.2.3</version></dependency> 写一个测试类,把excel输出到指定路径 public s…...

sam_out 目标检测的应用
缺点参考地址训练验证模型解析 缺点 词表太大量化才可 参考地址 https://aistudio.baidu.com/projectdetail/8103098 训练验证 import os from glob import glob import cv2 import paddle import faiss from out_yolo_model import GPT as GPT13 import pandas as pd imp…...

VLAN原理与配置
AUTHOR :闫小雨 DATE:2024-04-28 目录 VLAN的三种端口类型 VLAN原理 什么是VLAN 为什么使用VLAN VLAN的基本原理 VLAN标签 VLAN标签各字段含义如下: VLAN的划分方式 VLAN的划分包括如下5种方法: VLAN的接口链路类型 创建V…...

使用Spring Boot实现RESTful API
使用Spring Boot实现RESTful API 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨如何利用Spring Boot框架实现RESTful API,这是现…...
:八所高校)
中英双语介绍美国常春藤联盟( Ivy League):八所高校
中文版 常春藤联盟简介 常春藤联盟(Ivy League)是美国东北部八所私立大学组成的高校联盟。虽然最初是因体育联盟而得名,但这些学校以其学术卓越、历史悠久、校友杰出而闻名于世。以下是对常春藤联盟的详细介绍,包括其由来、成员…...

【计算机网络】常见的网络通信协议
目录 1. TCP/IP协议 2. HTTP协议 3. FTP协议 4. SMTP协议 5. POP3协议 6. IMAP协议 7. DNS协议 8. DHCP协议 9. SSH协议 10. SSL/TLS协议 11. SNMP协议 12. NTP协议 13. VoIP协议 14. WebSocket协议 15. BGP协议 16. OSPF协议 17. RIP协议 18. ICMP协议 1…...

java实现http/https请求
在Java中,有多种方式可以实现HTTP或HTTPS请求。以下是使用第三方库Apache HttpClient来实现HTTP/HTTPS请求的工具类。 优势和特点 URIBuilder的优势在于它提供了一种简单而灵活的方式来构造URI,帮助开发人员避免手动拼接URI字符串,并处理参…...

NC204871 求和
链接 思路: 对于一个子树来说,子树的节点就包括在整颗树的dfs序中子树根节点出现的前后之间,所以我们先进行一次dfs,用b数组的0表示区间左端点,1表示区间右端点,同时用a数组来标记dfs序中的值。处理完dfs序…...

git克隆代码warning: could not find UI helper ‘git-credential-manager-ui‘
git克隆代码warning: could not find UI helper ‘git-credential-manager-ui’ 方案 git config --global --unset credential.helpergit-credential-manager configure...

Generator 是怎么样使用的以及各个阶段的变化如何
Generators 是 JavaScript 中一种特殊类型的函数,可以在执行过程中暂停,并且在需要时恢复执行。它们是通过 function* 关键字来定义的。Generator 函数返回的是一个迭代器对象,通过调用该迭代器对象的 next() 方法来控制函数的执行。在调用 n…...

一文了解Java中 Vector、ArrayList、LinkedList 之间的区别
目录 1. 数据结构 Vector 和 ArrayList LinkedList 2. 线程安全 Vector ArrayList 和 LinkedList 3. 性能 插入和删除操作 随机访问 4. 内存使用 ArrayList 和 Vector LinkedList 5. 迭代器行为 ArrayList 和 Vector LinkedList 6. 扩展策略 ArrayList Vecto…...

【论文复现|智能算法改进】基于自适应动态鲸鱼优化算法的路径规划研究
目录 1.算法原理2.改进点3.结果展示4.参考文献5.代码获取 1.算法原理 SCI二区|鲸鱼优化算法(WOA)原理及实现【附完整Matlab代码】 2.改进点 非线性收敛因子 WOA 主要通过控制系数向量 A 来决定鲸鱼是搜索猎物还是捕获猎物,即系数向量 A 可…...

【Win测试】窗口捕获的学习笔记
2 辨析笔记 2.1 mss:捕获屏幕可见区域,不适合捕获后台应用 Claude-3.5-Sonnet: MSS库可以用来捕获屏幕上可见的内容;然而,如果游戏窗口被其他窗口完全遮挡或最小化,MSS将无法捕获到被遮挡的游戏窗口内容,而…...

PostgreSQL的学习心得和知识总结(一百四十七)|深入理解PostgreSQL数据库之transaction chain的使用和实现
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《PostgreSQL数据库内核分析》 2、参考书籍:《数据库事务处理的艺术:事务管理与并发控制》 3、PostgreSQL数据库仓库…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...
