【FedMut】Generalized Federated Learning via Stochastic Mutation
基于随机变异的泛化联邦学习
来源:AAAI2024
Abstract
问题:
FedAvg 将相同的全局模型派发给客户端进行本地训练,容易陷入尖锐解,导致训练出性能低下的全局模型
提出 FedMut:
本文提出了一种名为 FedMut 的新型FL方法,它根据梯度变化变异全局模型,以生成下一轮训练的几个中间模型。每个中间模型将被派发到客户端进行本地训练。最终,全局模型会收敛到突变模型范围内的平坦区域内
Introduction
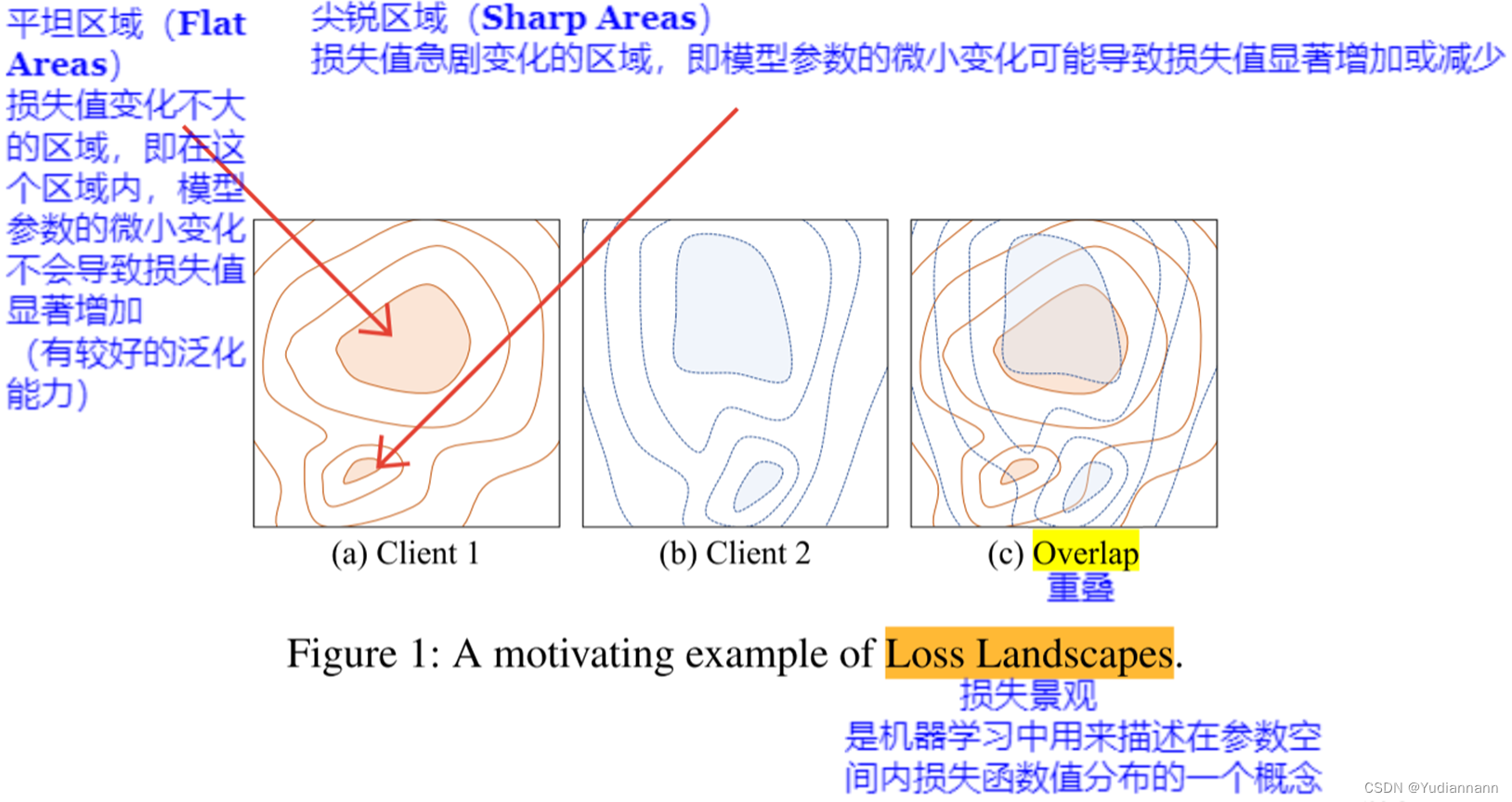
当模型收敛到两个客户端的平坦最优区域的重叠区域时,它在大多数客户端中都能实现高推理性能
Relate work
相关工作部分讨论了为了提高传统 FL 的推理性能,已经提出了许多 FL 优化方法。具体来说,这些方法可以分为三类,即
- 基于全局变量的 FL 方法
这类方法通常使用全局变量来指导本地训练朝相似方向进行
FedProx 使用本地模型与全局模型之间的平方距离作为近端项来正则化本地损失函数,从而稳定模型的收敛
SCAFFOLD 生成一个全局控制变量,并使用该变量在本地训练过程中纠正本地模型的优化方向
缺点:需要额外的通信开销来分发全局变量,或者在客户端上计算近端项的额外计算开销
- 基于设备分组的 FL 方法
这类方法尝试根据特定指标对设备进行分组,然后从不同分组中智能选择设备进行本地训练。大多数设备分组方法使用模型相似性作为分组指标,因为由于隐私保护的考虑,直接获取每个客户端的数据分布是困难的
CluSamp 使用样本大小或模型相似性作为客户端分组的指标
FedCluster 将客户端分组,并在每个 FL 轮次中循环地执行 FL
缺点:它们需要获取所有本地模型,这导致 FL 与安全聚合机制不兼容,从而可能引起潜在的隐私泄露风险
- 基于知识蒸馏的 FL 方法
这些方法采用著名的知识蒸馏技术来增强FL的推理性能。具体来说,它们使用一个表现良好的“教师模型”来指导“学生模型”的训练
FedAUX 使用辅助数据集进行数据依赖的蒸馏来初始化服务器模型
FedDF 使用集成模型作为“教师模型”,并使用未标记数据进行蒸馏,以加速FL训练
FedGen 使用内置生成器和代理数据集实现无数据蒸馏,解决了对额外数据集的需求问题
缺点:需要额外的计算开销来进行知识蒸馏和额外的数据集
Motivation
如果全局模型位于平坦区域,那么在其邻域内的模型仍然处于相同平坦区域的概率更高。相反,如果模型位于尖锐区域,那么在其邻域内的模型可能位于其他区域。基于这种直觉,我们变异全局模型以在其中生成多个模型,用于本地训练。当所有变异模型都位于相同区域时,我们可以获得一个泛化良好的全局模型,其邻域是平坦的

如图2(a)所示,云服务器通过模型变异过程生成四个变异模型。由于由变异模型组成的邻域小于初始全局模型所在的平坦区域,所有变异模型仍然位于这个平坦区域内。通过本地训练,所有变异模型都朝着平坦区域的中心优化,聚合后的全局模型相应地更新到平坦区域的中心
如图2(b)所示,由于由变异模型组成的邻域大于平坦区域,三个变异模型位于另一个区域而不是初始全局模型所在的尖锐区域。通过本地训练,三个变异模型朝着平坦区域优化,只有一个变异模型在尖锐区域进行优化。因此,聚合后的全局模型朝平坦区域移动
Settings
- 随机梯度下降(SGD)优化器
- learning rate = 0.01
- momentum = 0.9
- batch size = 50
- epoch = 5
数据集
- CIFAR-10
- CIFAR-100
- Shakespeare
模型
在 CIFAR-10 和 CIFAR-100 上
- CNN、ResNet-18
在 Shakespeare 上
- LSTM
动机验证
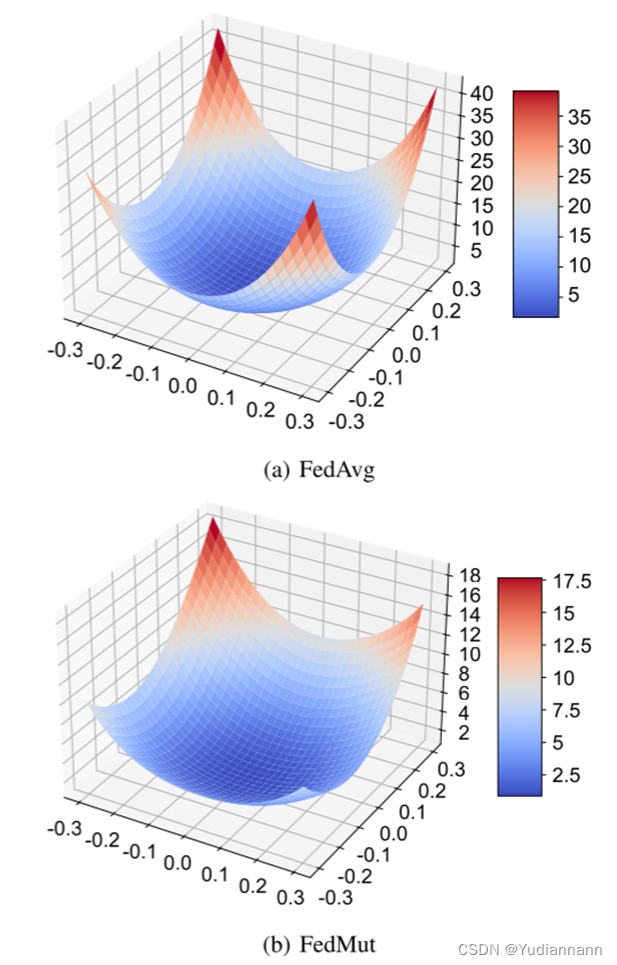
实验结果

消融研究
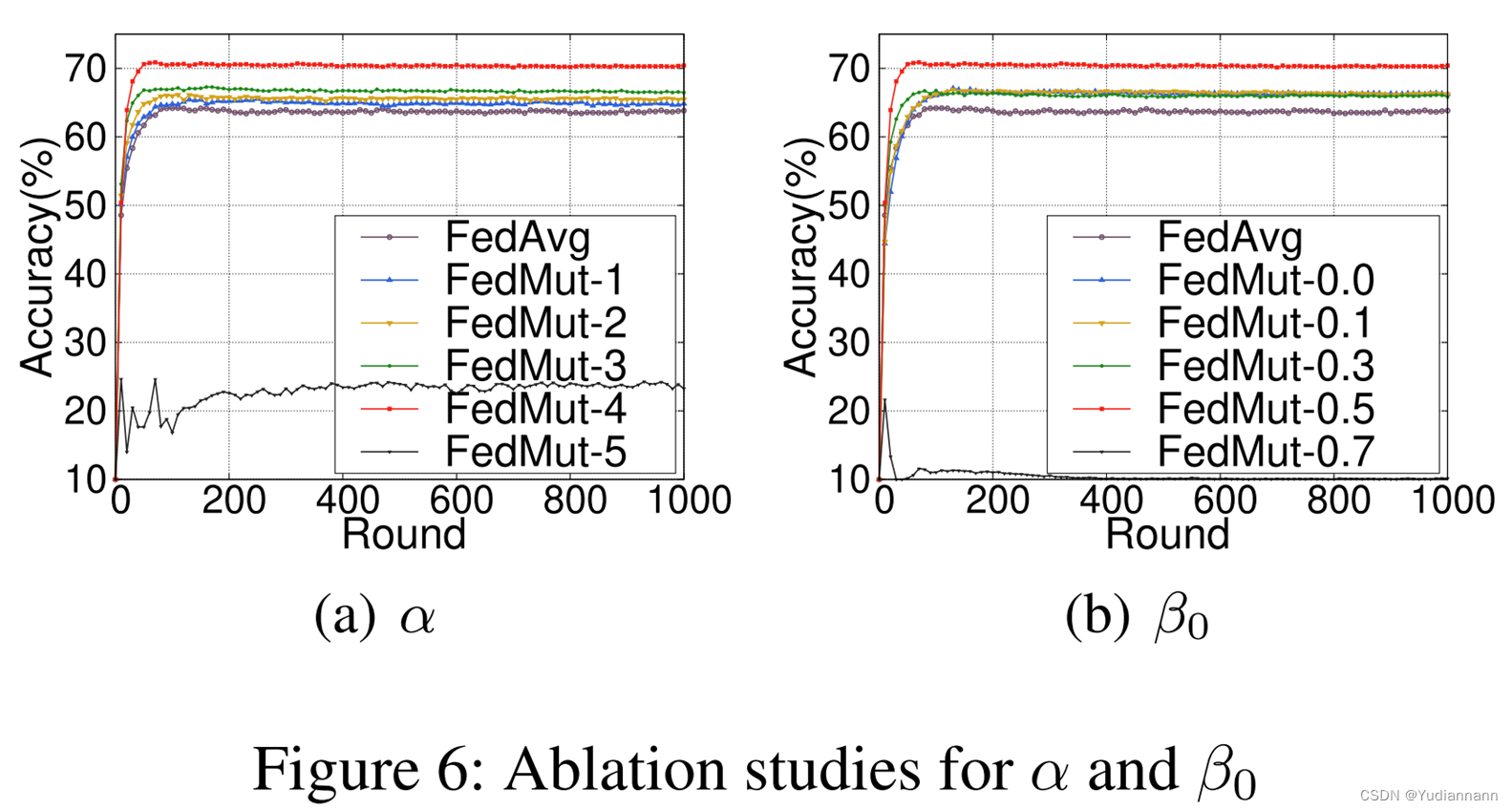
相关文章:

【FedMut】Generalized Federated Learning via Stochastic Mutation
基于随机变异的泛化联邦学习 来源:AAAI2024 Abstract 问题: FedAvg 将相同的全局模型派发给客户端进行本地训练,容易陷入尖锐解,导致训练出性能低下的全局模型 提出 FedMut: 本文提出了一种名为 FedMut 的新型FL方法…...

在线教育项目(一):如何防止一个账号多个地方登陆
使用jwt做验证,使用账号作为redis中的key,登录的时候生成token放到redis中,每次申请资源的时候去看token 有没有变,因为token每次登录都会去覆盖,只要第二次登录token就不一样了...
旋转变压器软件解码simulink仿真
1.介绍 旋转变压器是一种精密的位置、速度检测装置,尤其适用于高温、严寒、潮湿、高速、振动等环境恶劣、旋转编码器无法正常工作的场合。旋转变压器在使用时并不能直接提供角度或位置信息,需要特殊的激励信号和解调、计算措施,才能将旋转变压…...

LeetCode 1321, 209, 102
目录 1321. 餐馆营业额变化增长题目链接表要求知识点思路代码 209. 长度最小的子数组题目链接标签暴力法思路代码 滑动窗口思路代码 102. 二叉树的层序遍历题目链接标签思路代码 1321. 餐馆营业额变化增长 题目链接 1321. 餐馆营业额变化增长 表 表Customer的字段为custome…...

vant ( weapp ) - - - - - van-tabs组件选中下划线初始位置异常
这里写自定义目录标题 1. 当前效果展示2. 官方解释 & 方案 1. 当前效果展示 明显可以看到框内的光标位置偏移了,但当切换一次之后就会显示正常。 只有初次打开的时候,才会出现上述问题。 代码如下: <van-popup show"{{ makeSho…...
)
007 栈(lua)
文章目录 Lua本身支持动态数组,通过表(table)实现,它类似于Java中的ArrayList。Lua的表是灵活的数组和字典的混合体。对于栈的实现,我们可以简单地使用一个表来模拟。 这里是一个简单的Lua栈实现,它包含了p…...

SQL中Order by详解
在 MySQL 中,ORDER BY 语句用于对查询结果进行排序。 语法: SELECT column1, column2,... FROM table_name ORDER BY column_name [ASC | DESC];以下是对其主要部分的详细解释: column_name :指定要依据其进行排序的列名。 ASC…...

【git】存在git LFS文件时如何处理
目录 1. 安装 Git LFS2. 初始化 Git LFS3. 跟踪大文件4. 添加和提交文件5. 克隆和拉取包含 LFS 文件的仓库 1. 安装 Git LFS 首先,你需要在你的系统上安装 Git LFS。你可以使用以下命令来安装: 在 Linux 上 # 对于基于 Debian 的系统 (如 Ubuntu) sud…...
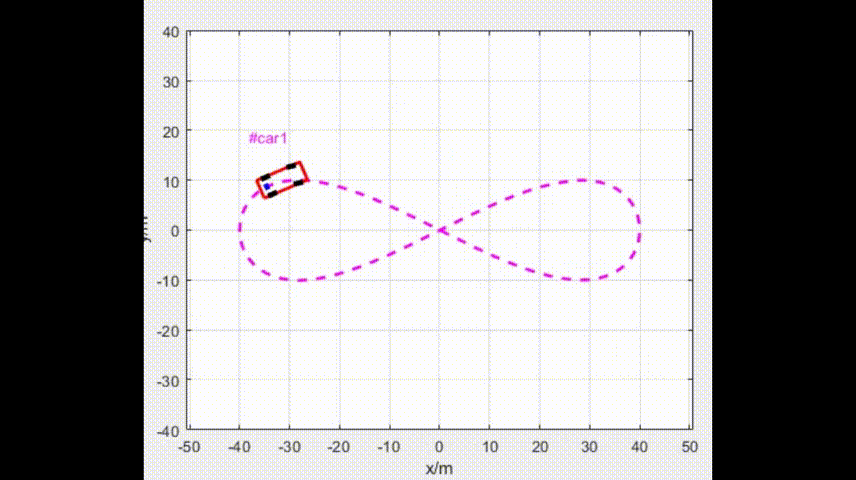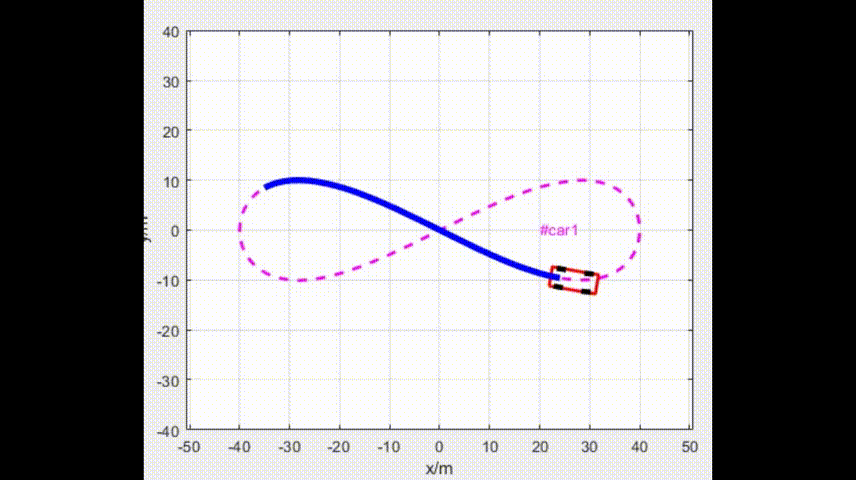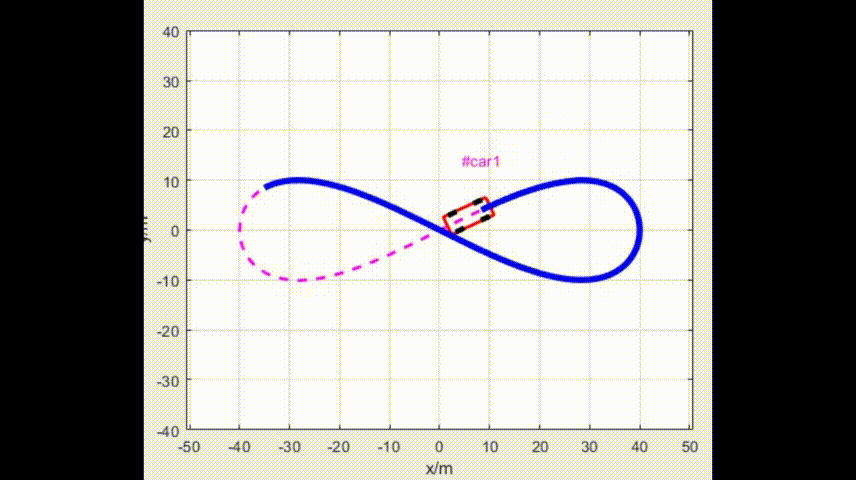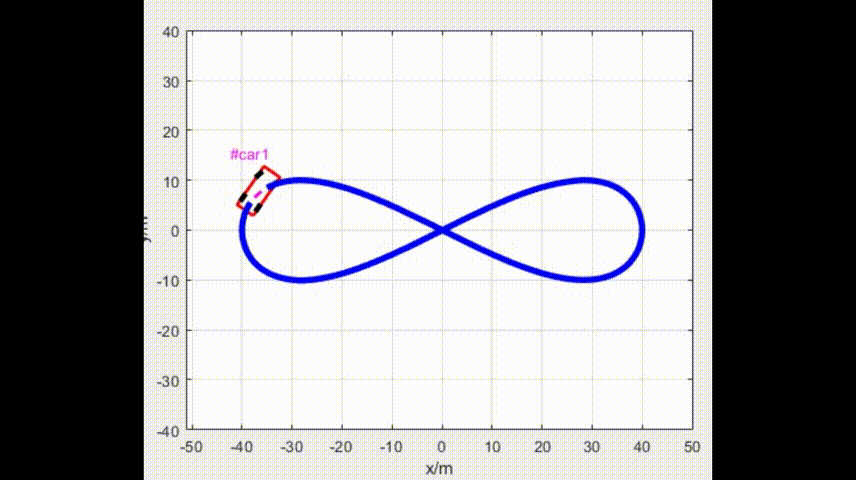
面向阿克曼移动机器人(自行车模型)的LQR(最优二次型调节器)路径跟踪方法
线性二次调节器(Linear Quadratic Regulator,LQR)是针对线性系统的最优控制方法。LQR 方法标准的求解体系是在考虑到损耗尽可能小的情况下, 以尽量小的代价平衡其他状态分量。一般情况下,线性系统在LQR 控制方法中用状态空间方程描…...

【运维】在 Docker 容器中指定 UTF-8 编码:方法与技巧
在 Docker 容器中指定 UTF-8 编码:方法与技巧 在日常开发中,我们常常需要确保应用程序能正确处理各种字符编码,尤其是 UTF-8 编码。在 Docker 容器中运行应用程序时,正确设置字符编码尤为重要,因为容器通常是跨平台、…...

primetime中cell和net的OCV
文章目录 前言一、Cell OCV1. POCV coefficient file2. POCV Slew-Load Table in Liberty Variation Format(LVF lib) 二、Net OCV三、如何check OCV是否已加上?总结 前言 在生产中,外界环境的各种变化,比如PVT&#…...
FlinkX学习
FlinkX学习 FlinkX安装 由于flinkx已经改名chunjun 官网已不存在 (https://gitee.com/lugela/flinkx#flinkx)这里可以看到flinkx的操作文档 1、上传并解压 unzip flinkx-1.10.zip -d /usr/local/soft/2、配置环境变量 FLINKX_HOME/usr/local/soft/flinkx-1.10 export PATH$F…...

新书速览|解密AI绘画与修图: Stable Diffusion+Photoshop
《解密AI绘画与修图: Stable DiffusionPhotoshop》 本书内容 《解密AI绘画与修图:Stable DiffusionPhotoshop》全面介绍了Photoshop和Stable Diffusion的交互方式,以及各自的AI功能和具体使用方法。除了讲解功能,还通过实际案例加…...

1111111111111
计算机视觉技术在医疗领域的应用正迅速成为推动医疗进步的关键力量。通过高级图像处理和分析,这项技术在医学影像分析(包括CT、MRI和X光图像)、实时手术辅助、患者监测和护理、以及疾病早期诊断等方面展现出巨大的潜力。然而,随着…...

云原生概念
云原生是一种新型的技术体系和方法论,旨在充分利用云计算环境的优势,使应用程序更具有弹性、可伸缩性、可靠性和效率。以下是云原生的详细解释: 定义: 云原生是一种基于分布部署和统一运管的分布式云,以容器、微服务、…...

NoSQL之Redis高可用与优化
一、Redis高可用 在web服务器中,高可用是指服务器可以正常访问的时间,衡量的标准是在多长时间内可以提供正常服务(99.9%、99.99%、99.999%等等)。 但是在Redis语境中,高可用的含义似乎要宽泛一些,除了保证…...

MySQL 常见存储引擎详解(一)
本篇主要介绍MySQL中常见的存储引擎。 目录 一、InnoDB引擎 简介 特性 最佳实践 创建InnoDB 存储文件 二、MyISAM存储引擎 简介 特性 创建MyISAM表 存储文件 存储格式 静态格式 动态格式 压缩格式 三、MEMORY存储引擎 简介 特点 创建MEMORY表 存储文件 内…...

Leetcode 股票买卖
买卖股票最佳时机 I II 不限制交易次数 prices [7,1,5,3,6,4] 启发思路:最后一天发生了什么? 从第0天到第5天结束时的利润 从第0天到第4天结束时的利润 第5天的利润 (第5天的利润:0/-4/4) 关键词:天…...
小白学习手册:轻松理解MQ消息队列
目录 # 开篇 RabbitMQ介绍 通讯概念 1. 初始MQ及类型 2. MQ的架构 2.1 RabbitMQ的结构和概念 2.2 RabbitMQ消息流示意图 3. MQ下载使用 3.1 Docker下载MQ参考 3.2 进入RabbitMQ # 开篇 MessagesQueue 是一个抽象概念,用于描述消息队列系统的一般特性和功能…...

electron线上更新
一、安装electron-updater npm install --save electron-updater二、在main.js中引入使用 import { autoUpdater } from electron; if (!isDev) {const serverUrl https://your-update-server.com; // 自定义更新服务器地址或GitHub Releases地址autoUpdater.setFeedURL(${…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
