16、matlab求导、求偏导、求定积分、不定积分、数值积分和数值二重积分
0)前言
在MATLAB中,对函数进行不同形式的求导、求积分操作是非常常见的需求,在工程、科学等领域中经常会用到。以下是关于求导、求积分以及数值积分的简介:
-
求导:在MATLAB中可以使用
diff函数对函数进行求导操作。diff函数有多种用法,可以求一阶、高阶导数,也可以求偏导数。例如,求函数f(x)的一阶导数可以使用diff(f, x),求函数f(x, y)对x的偏导数可以使用diff(f, x)。 -
求定积分和不定积分:在MATLAB中可以使用
int函数对函数进行定积分和不定积分的计算。int函数可以对输入的表达式进行积分计算。例如,求函数f(x)在区间[a, b]上的定积分可以使用int(f, a, b),求函数f(x)的不定积分可以使用int(f, x)。 -
数值积分:在MATLAB中,可以使用
integral函数进行数值积分计算。integral函数可以对给定的函数进行数值积分计算,常用于无法通过解析方法得到积分的情况。例如,对函数f(x)在区间[a, b]上进行数值积分可以使用integral(@(x) f(x), a, b)。 -
数值二重积分:在MATLAB中,可以使用
integral2函数进行数值二重积分计算。integral2函数可以对给定的二元函数进行数值积分计算,常用于求解二维区域上的积分。例如,对二元函数f(x, y)在区域D上进行数值二重积分可以使用integral2(@(x, y) f(x, y), x_min, x_max, y_min, y_max)。
以上是对MATLAB中求导、求积分操作的简介,通过灵活使用这些函数,可以方便地进行各种类型的导数和积分计算。值得注意的是,在进行数值积分时,可以根据具体情况选择适合的数值积分方法,以获得更精确和高效的计算结果。
1、matlab求导,diff()函数
1)一阶导数
语法:diff(f(x)):求一阶导数 //diff(f(x),n):求n阶导数(n为具体正整数)
以函数(cos(x)+sin(x)-x^2)的一阶导数为例
一阶导数代码:
yms x;%声明符号变量x
f(x)=cos(x)+sin(x)-x^2;%定义原式子
dy=diff(f(x))%求一阶导数dy =cos(x) - 2*x - sin(x)2)n阶倒数
以函数(cos(x)+sin(x)-x^2)二三阶倒数为例
二三阶导数代码:
syms x;%声明符号变量x
f(x)=cos(x)+sin(x)-x^2;%定义原式子
dy1=diff(f(x),2)
% pretty(dy1)
dy2=diff(f(x),3)dy1 =- cos(x) - sin(x) - 2dy2 =sin(x) - cos(x)2、matlab求偏导,diff()函数
语法:diff(f(x)):求一阶导数 //diff(f(x),n):求n阶导数(n为具体正整数)
以函数(f(x1,x2)=sin(x1)+exp(x2))求解x1和x2偏倒为例
1)一阶偏导
x1求偏导代码:
syms x1 x2;%声明符号变量x1\x2
f(x1,x2)=sin(x1)+exp(x2);%定义原函数
%求一阶偏导
dy1=diff(f(x1,x2),x1)dy1 =cos(x1)x2求偏导代码:
syms x1 x2;%声明符号变量x1\x2
f(x1,x2)=sin(x1)+exp(x2);%定义原函数
dy2=diff(f(x1,x2),x2)dy2 =exp(x2)2)n阶偏导
x1二阶偏导代码:
syms x1 x2;%声明符号变量x1\x2
f(x1,x2)=sin(x1)+exp(x2);%定义原函数
dy3=diff(f(x1,x2),x1,2)dy3 =-sin(x1)x2三阶偏导代码:
syms x1 x2;%声明符号变量x1\x2
f(x1,x2)=sin(x1)+exp(x2);%定义原函数
dy4=diff(f(x1,x2),x2,3)dy4 =exp(x2)3、matlab求积分,int()函数
1)不定积分求解
语法:牛顿——莱布尼兹公式求解积分
代码:
syms x;%声明变量x
y1=x^2;%定义原式
fy1=int(y1,x)%不定积分fy1 =x^3/32)定积分求解
代码:
syms x;%声明变量x
y1=x^2;%定义原式
% fy1=int(y1,x)%不定积分
fy2=int(y1,x,0,1)%定积分fy2 =1/3syms x;%声明变量x
y1=x^2;%定义原式
% fy1=int(y1,x)%不定积分
% fy2=int(y1,x,0,1)%定积分
fy3=int(y1,x,-inf,+inf)fy3 =Inf4、数值积分
1)梯形法计算积分 trapz()函数
语法:I=trapz(x,y) %适用于被积函数为离散数据
代码:
format long%显示格式设置
fy=@(x)sin(x)./x%@句柄的用法
x1=pi/6:pi/100:pi;
y1=fy(x1);
%绘图
bar(y1)
%定积分
s1=trapz(x1,y1)fy =包含以下值的 function_handle:@(x)sin(x)./xs1 =1.336217975152237视图效果:

2)基于变步长辛普森计算积分
语法:[I,n]=quad(‘fname’,a,b,Tol,trace)%I积分值/n积分函数调用次数
参数介绍fname:被积函数名 a,b积分界限 TOL精度 trace是否展现积分过程
基于变步长辛普森计算积分与梯形法计算积分对比代码:
fy=@(x)sin(x)./x%被积函数
s=quad(fy,pi/6,pi,0.00001,1)%变步长辛普森计算积分
x1=pi/6:pi/100:pi;
y1=fy(x1);
s1=trapz(x1,y1)%梯形法计算积分fy =包含以下值的 function_handle:@(x)sin(x)./x9 0.5235987756 7.10994777e-01 0.619018804711 1.2345935530 1.19600432e+00 0.626190692913 2.4305978762 7.10994777e-01 0.0910383671s =1.336247864730292s1 =1.3362179751522375、数值二重积分 dblquad()函数
语法:I=dblquad(f,a,b,c,d,tol,method),求f(x,y)在[a,b]、[c,d]区域上的二重积分
TOL精度 Method:计算一维积分(quad/quadl)
代码:
f=@(x,y)exp(x.^2).*sin(x.^2+y.^2)I1=dblquad(f,-2,2,-1,1)I2=dblquad(f,-2,2,-1,1,1e-9,'quadl')I3=dblquad(f,-2,2,-1,1,1e-9,'quad')%默认f =包含以下值的 function_handle:@(x,y)exp(x.^2).*sin(x.^2+y.^2)I1 =-9.400793312509709I2 =-9.400792842118586I3 =-9.4007928422963156、数值积分 integral()函数
语法:q = integral(fun,xmin,xmax,Name,Value)
代码:
fun = @(x) exp(-x.^2).*log(x).^2;
q = integral(fun,0,Inf)
q1 = integral(fun,0,Inf,'RelTol',1e-9)q =1.947522220295560q1 =1.9475221803142557、二重积分 integral2()函数
语法:q = integral2(fun,xmin,xmax,ymin,ymax,Name,Value)
代码:
fun = @(x,y) 1./( sqrt(x + y) .* (1 + x + y).^2 );
q1= integral2(fun,0,1,0,1)
q2= integral2(fun,0,1,0,1,'RelTol',1e-9)q1 =0.369530192486637q2 =0.3695301805005568、总结
在MATLAB中,求导、求偏导、求定积分、不定积分、数值积分和数值二重积分是信号处理、数学建模等领域中常用的操作。以下是对这些操作的总结:
-
求导:
- 一阶导数:使用
diff函数。 - 多阶导数:连续多次使用
diff函数。 - 求偏导数:指定对哪个变量求偏导数。
- 一阶导数:使用
-
求定积分和不定积分:
- 定积分:使用
int函数,指定积分上下限。 - 不定积分:使用
int函数,只指定被积分的变量。
- 定积分:使用
-
数值积分:
- 一维数值积分:使用
integral函数,指定被积函数和积分区间。 - 二维数值积分:使用
integral2函数,指定被积函数和积分区域。
- 一维数值积分:使用
-
注意事项:
- 在使用数值积分函数时,可以指定积分精度和其他参数,以获得更精确的结果。
- 对于复杂函数或区域,可以使用数值积分来近似求解积分值。
- 在处理数值积分结果时,要注意结果的有效性和精度,可以使用MATLAB的调试工具进行验证。
综上所述,MATLAB提供了丰富的函数和工具,可以方便地进行导数、积分和数值积分等操作。这些操作在数学建模、信号处理、科学计算等领域中具有重要的应用意义,能够帮助用户进行数据分析、模拟和预测等工作。在实际应用中,根据具体需求选择合适的函数和方法,以实现准确、高效的数据处理和计算。
相关文章:

16、matlab求导、求偏导、求定积分、不定积分、数值积分和数值二重积分
0)前言 在MATLAB中,对函数进行不同形式的求导、求积分操作是非常常见的需求,在工程、科学等领域中经常会用到。以下是关于求导、求积分以及数值积分的简介: 求导:在MATLAB中可以使用diff函数对函数进行求导操作。diff…...
MySQL 9.0创新版发布!功能又进化了!
作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验, Oracle、PostgreSQL ACE CSDN博客专家及B站知名UP主,全网粉丝10万 擅长主流Oracle、MySQL、PG、高斯及Greenplum备份恢复, 安装迁移,性能优化、故障…...

后端系统的安全性
后端系统的安全性 后端系统的安全性是任何Web应用或服务的核心组成部分,它涉及保护数据、用户隐私以及系统免受恶意攻击。以下是后端安全的一些关键点: 认证和授权:确保只有经过身份验证的用户才能访问特定资源。这通常包括使用用户名/密码…...

.net 百度翻译接口核心类
百度翻译api :http://developer.baidu.com/wiki/index.php?title帮助文档首页/百度翻译/翻译AP 核心翻译类 using System; using System.Collections.Generic; using System.Linq; using System.Text; using Newtonsoft.Json; using System.Net; using System.I…...

安卓应用开发学习:通过腾讯地图SDK实现定位功能
一、引言 这几天有些忙,耽误了写日志,但我的学习始终没有落下,有空我就会研究《 Android App 开发进阶与项目实战》一书中定位导航方面的内容。在我的手机上先后实现了“获取经纬度及地理位置描述信息”和“获取导航卫星信息”功能后&#x…...
iptable精讲
SNAT策略 SNAT策略的典型应用环境 局域网主机共享单个公网IP地址接入Internet SNAT策略的原理 源地址转换,Source Network Address Translantion 修改数据包的源地址 部署SNAT策略 1.准备二台最小化虚拟机修改主机名 主机名:gw 主机名࿱…...
2024 年如何构建 AI 软件
人工智能 (AI) 是当今 IT 行业最热门的话题,受到大型科技公司、大型企业和投资者的青睐。如果有人不参与 AI,他们就出局了。虽然“AI 泡沫”一词尚未公开使用,但街上的每个人都可能听说过 AI 将取代我们的工作(可能不会࿰…...

Python实战,桌面小游戏,剪刀石头布
注意:本文的下载教程,与以下文章的思路有相同点,也有不同点,最终目标只是让读者从多维度去熟练掌握本知识点。 下载教程: Python项目开发实战_桌面小游戏-剪刀石头布_编程案例解析实例详解课程教程.pdf 创建一个基于Python的桌面小游戏“剪刀石头布”是一个很好的编程实践…...

Hadoop权威指南-读书笔记-01-初识Hadoop
Hadoop权威指南-读书笔记 记录一下读这本书的时候觉得有意思或者重要的点~ 第一章—初识Hadoop Tips: 这个引例很有哲理嘻嘻😄,道出了分布式的灵魂。 1.1 数据!数据! 这一小节主要介绍了进入大数据时代,面…...
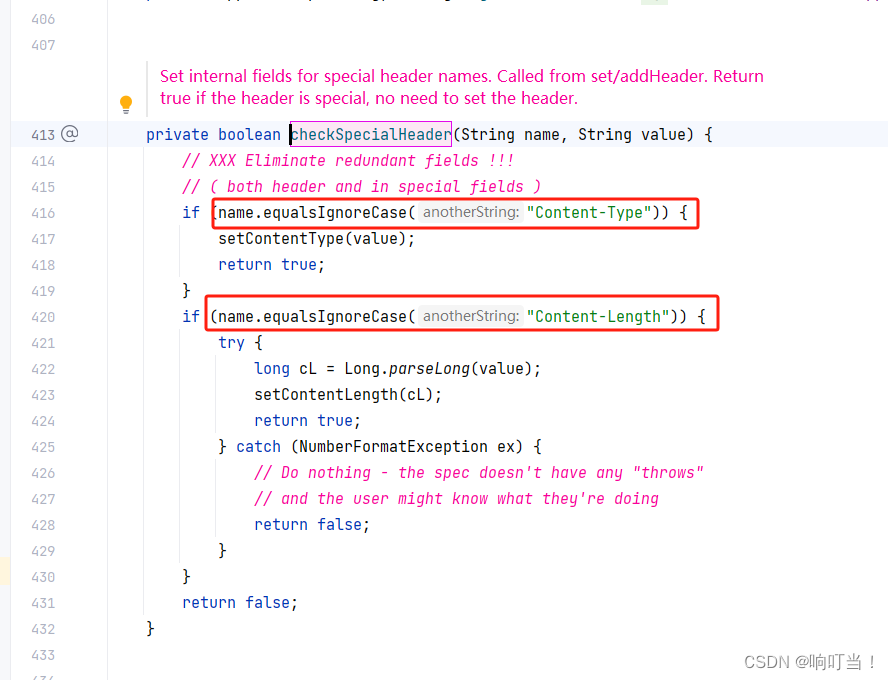
HttpServletResponse设置headers返回,发现headers中缺少“Content-Length“和“Content-Type“两个参数。
业务中需要将用httpUtils请求返回的headers全部返回,塞到HttpServletResponse中,代码如下: HttpServletResponse response;// 返回headers Arrays.stream(httpResponse.getHeaders()).forEach(header -> response.setHeader(header.getNa…...

GraphPad Prism生物医学数据分析软件下载安装 GraphPad Prism轻松绘制各种图表
Prism软件作为一款功能强大的生物医学数据分析与可视化工具,其绘图功能尤为突出。该软件不仅支持绘制基础的图表类型,如直观明了的柱状图、展示数据分布的散点图,以及描绘变化趋势的曲线图,更能应对复杂的数据呈现需求,…...

7/1 uart
uart4.c #include "uart4.h"//UART4_RX > PB2 //UART4_TX > PG11char rebuf[51] {0}; //rcc/gpio/uart4初始化 void hal_uart4_init() {/********RCC章节初始化*******///1.使能GPIOB组控制器 MP_AHB4ENSETR[1] 1RCC->MP_AHB4ENSETR | (0x1 << 1)…...
zdppy_api+vue3+antd开发前后端分离的预加载卡片实战案例
后端代码 import api import upload import timesave_dir "uploads"async def rand_content(request):key api.req.get_query(request, "key")time.sleep(0.3)return api.resp.success(f"{key} " * 100)app api.Api(routes[api.resp.get(&qu…...
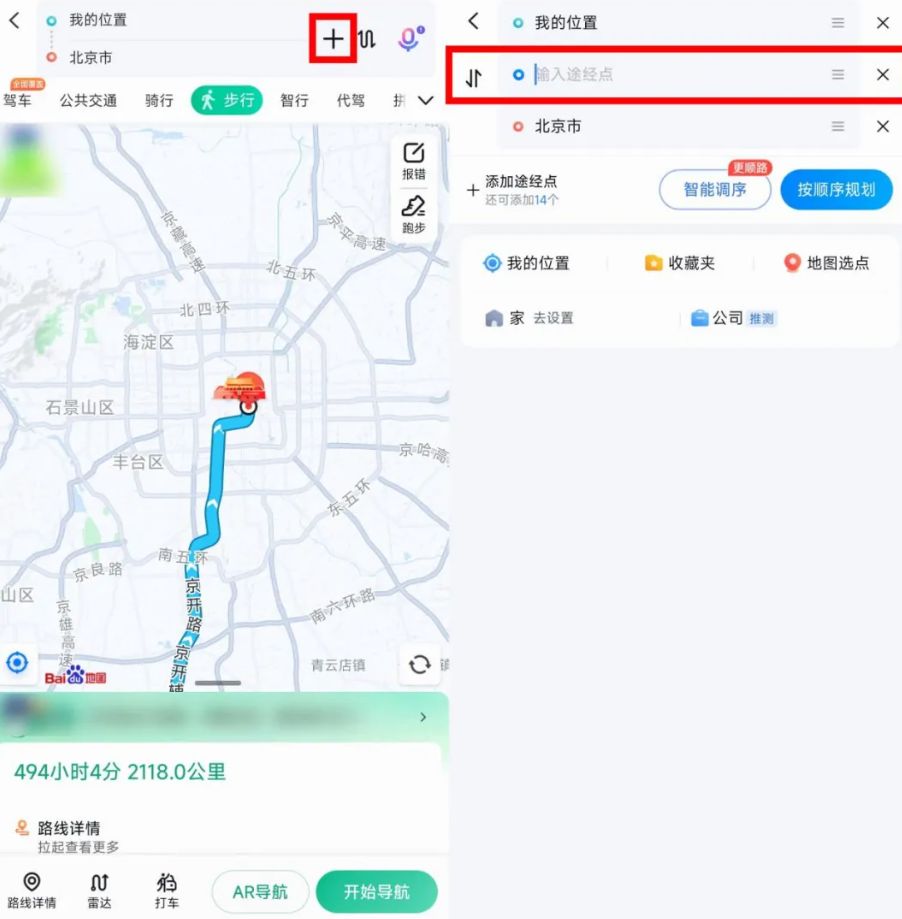
别小看手机导航,这些隐藏功能大部分人可能都不知道
在科技日新月异的今天,手机导航已经成为我们日常生活中不可或缺的一部分。它不仅仅是指引我们前往目的地的工具,更隐藏着许多黑科技功能,极大地丰富了我们的出行体验。 今天,让我们一起探索手机导航中那些鲜为人知却大有用处的隐…...
)
Lua实现链表(面向对象应用)
Lua实现面向对象 面向对象核心三要素Lua面向对象大致原理面向对象示例继承与多态示例 面向对象核心三要素 1.封装:对一个事物的抽象为一些属性和行为动作的集合,封装将属性和行为动作(操作数据的方法)绑定在一起,并隐藏…...

每隔一个小时gc一次的问题
原文地址https://www.cnblogs.com/jiangxinlingdu/p/7581064.html 设置一下这个 -XX:ExplicitGCInvokesConcurrent 或 -XXExplicitGCInvokesConcurrentAndUnloadsClasses 并且检查一下,并下面的值设置变大 java.rmi.dgc.leaseValue sun.rmi.dgc.client.gcInterv…...
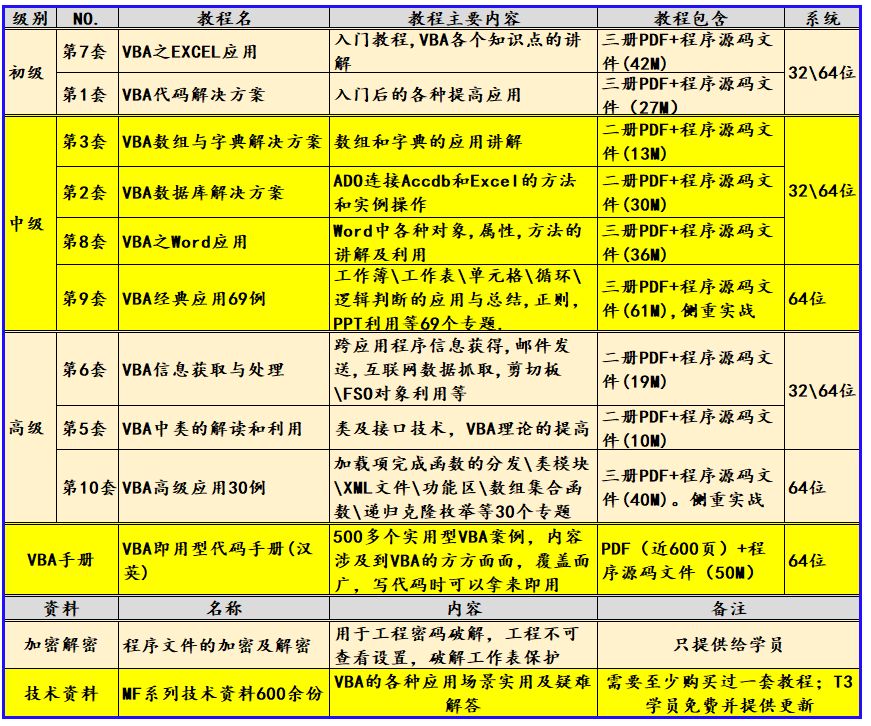
VBA数据库解决方案第十二讲:如何判断数据库中数据表是否存在
《VBA数据库解决方案》教程(版权10090845)是我推出的第二套教程,目前已经是第二版修订了。这套教程定位于中级,是学完字典后的另一个专题讲解。数据库是数据处理的利器,教程中详细介绍了利用ADO连接ACCDB和EXCEL的方法…...
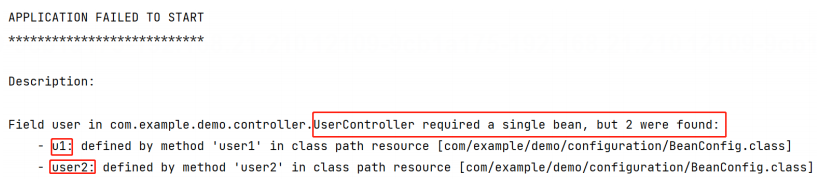
五、Spring IoCDI ★ ✔
5. Spring IoC&DI 1. IoC & DI ⼊⻔1.1 Spring 是什么?★ (Spring 是包含了众多⼯具⽅法的 IoC 容器)1.1.1 什么是容器?1.1.2 什么是 IoC?★ (IoC: Inversion of Control (控制反转))总…...

计算机网络八股文
计算机网络体系架构? OSI结构:理论上的 7应用层:定义了应用进程间通信和交互的规则,常见协议有HTTP、SFTP、DNS、WebSocket6表示层:数据的表示、安全、压缩。确保一个系统的应用层所发消息能被另一个系统的应用层读取…...
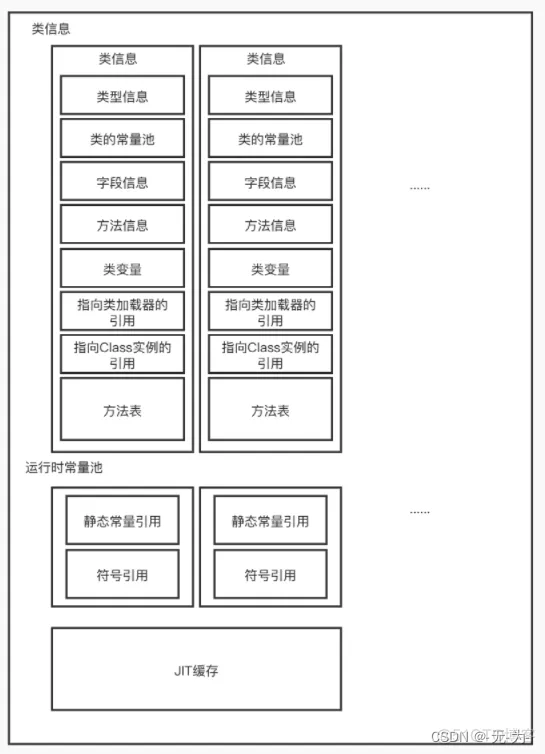
科普文:一文搞懂jvm原理(四)运行时数据区
概叙 科普文:一文搞懂jvm(一)jvm概叙-CSDN博客 科普文:一文搞懂jvm原理(二)类加载器-CSDN博客 科普文:一文搞懂jvm原理(三)执行引擎-CSDN博客 前面我们介绍了jvm,jvm主要包括两个子系统和两个组件: Class loader(类…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
