Scrapy实现关键词搜索的数据爬取
爬虫技术对于从互联网上获取数据和信息非常重要,而scrapy作为一款高效、灵活和可扩展的网络爬虫框架,能够简化数据爬取的过程,对于从互联网上爬取数据的工作非常实用。本文将介绍如何使用scrapy实现关键词搜索的数据爬取。
- Scrapy的介绍
Scrapy是一款基于Python语言的网络爬虫框架,它具有高效、灵活和可扩展等特点,可用于数据抓取、信息管理和自动化测试等多种任务。 Scrapy中包含了各种各样的组件,例如爬虫解析器、网络抓取器、数据处理器等,通过这些组件可以实现高效的网络爬取和数据处理。
- 实现关键词搜索
在使用Scrapy实现关键词搜索的数据爬取之前,需要对Scrapy框架的架构以及requests、BeautifulSoup等基础库有所了解。具体实现步骤如下:
(1)创建项目
在命令行中输入如下命令,创建一个Scrapy项目:
scrapy startproject search
该命令会在当前目录下创建一个名为search的目录,该目录包含了一个settings.py文件和一个名为spiders的子目录。
(2)爬虫编写
在spiders子目录下新建一个名为searchspider.py的文件,在该文件中编写爬虫的代码。
首先定义了要搜索的关键词:
search_word = 'Scrapy'
然后定义了数据爬取的URL:
start_urls = [
| 1 |
|
]
该代码会从百度搜索结果的前10页中爬取数据。
接着,我们需要构建爬虫的解析器,在该解析器中使用了BeautifulSoup库对网页进行解析,然后从中抽取出标题和URL等信息:
def parse(self, response):
| 1 2 3 4 5 6 7 |
|
在进行网页解析时使用了BeautifulSoup库,该库可以充分利用Python语言的优势进行快速的网页解析,提取出需要的数据。
最后,我们需要将抓取到的数据存储到本地文件中,在pipeline.py文件中定义数据处理器:
class SearchPipeline(object):
| 1 2 3 |
|
')
该代码针对每个爬取到的数据进行处理,将标题和URL分别写入到result.txt文件中。
(3)运行爬虫
在命令行中进入到爬虫项目所在的目录,并输入如下命令来运行爬虫:
scrapy crawl search
通过该命令即可启动爬虫程序,程序将自动从百度搜索结果中爬取与关键词Scrapy相关的数据,并将结果输出到指定的文件中。
- 结论
通过使用Scrapy框架和BeautifulSoup等基础库,我们可以非常方便地实现关键词搜索的数据爬取。Scrapy框架具有高效、灵活和可扩展等特点,前往体验电商数据体验API接口地址,使得数据爬取过程更为智能化和高效化,非常适合从互联网上获取大量数据的应用场景。在实际应用中,我们可以通过优化解析器、改进数据处理器等方式进一步提高数据爬取的效率和质量。
相关文章:

Scrapy实现关键词搜索的数据爬取
爬虫技术对于从互联网上获取数据和信息非常重要,而scrapy作为一款高效、灵活和可扩展的网络爬虫框架,能够简化数据爬取的过程,对于从互联网上爬取数据的工作非常实用。本文将介绍如何使用scrapy实现关键词搜索的数据爬取。 Scrapy的介绍 Sc…...

【Linux】ip命令详解
Linux中的ip命令是一个功能强大的网络配置工具,用于显示或操作路由、网络设备、策略路由和隧道。以下是关于ip命令的详细解释: 一、ip命令介绍 简介:ip命令是一个用于显示或操作路由、网络设备、策略路由和隧道的Linux命令行工具。它取代了早期的ifconfig命令,并提供了更多…...
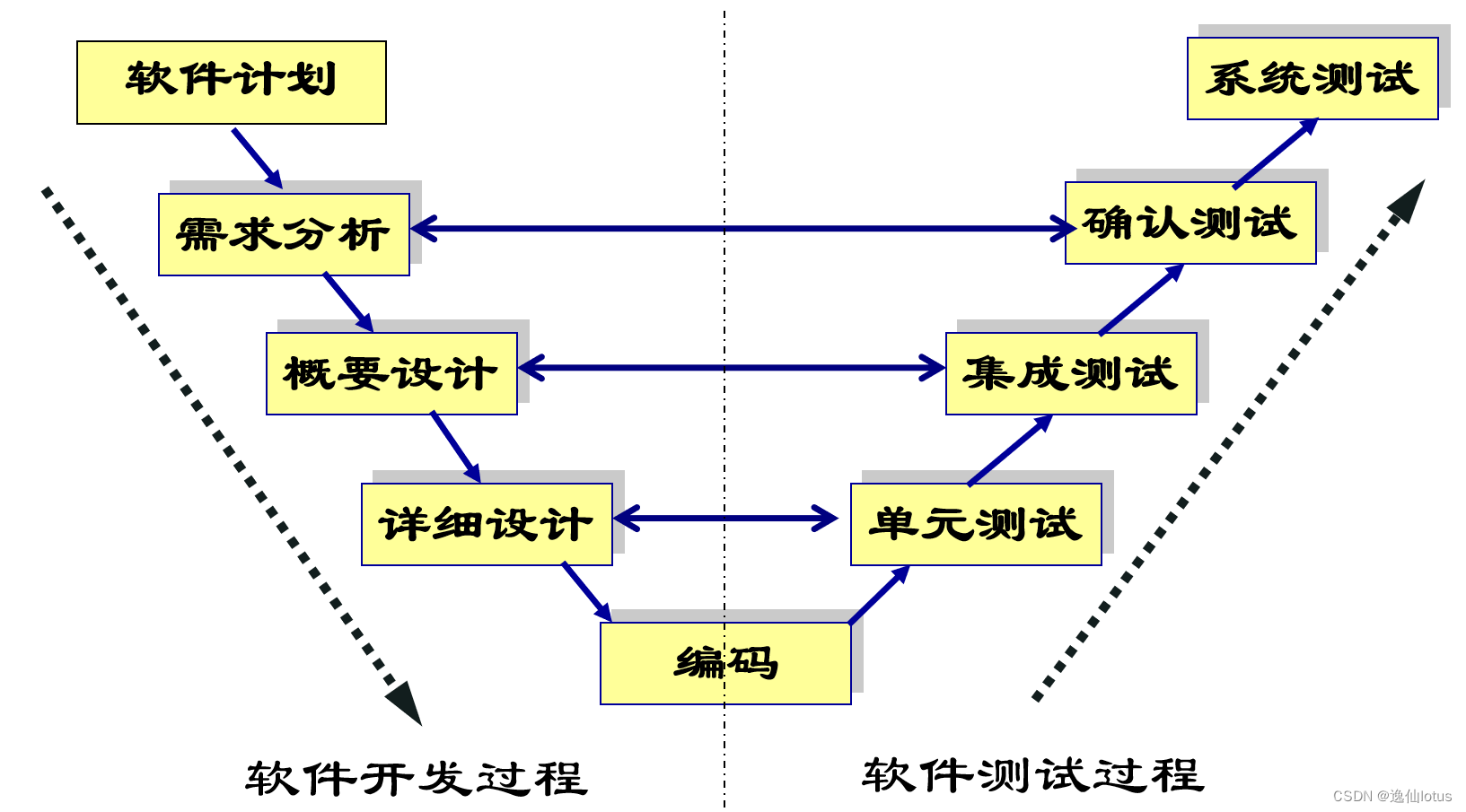
软降工程学系统实现
一、程序编码 程序编码是设计的继续,将软件设计的结果翻译成用某种程序设计语言描述的源代码。 程序编码涉及到方法、工具和过程。 程序设计风格和程序设计语言的特性会深刻地影响软件的质量和可维护性。 要求源程序具有良好的结构性和设计风格。 程序设计风格…...

001 SpringMVC介绍
文章目录 基础概念介绍BS和CS开发架构应用系统三层架构MVC设计模式 SpringMVC介绍SpringMVC是什么SpringMVC与Spring的联系为什么要学习SpringMVC 六大组件介绍六大组件(MVC组件其他三大组件)说明 基础概念介绍 BS和CS开发架构 一种是C/S架构,也就是客户端/服务器…...

深入解析scikit-learn中的交叉验证方法
交叉验证是机器学习中用于评估模型性能的重要技术,它可以帮助我们理解模型在未知数据上的泛化能力。scikit-learn(简称sklearn)是一个广泛使用的Python机器学习库,提供了多种交叉验证方法。本文将详细介绍scikit-learn中提供的交叉…...
分布式kettle调度管理平台简介
介绍 Kettle(也称为Pentaho Data Integration)是一款开源的ETL(Extract, Transform, Load)工具,由Pentaho(现为Hitachi Vantara)开发和维护。它提供了一套强大的数据集成和转换功能,…...
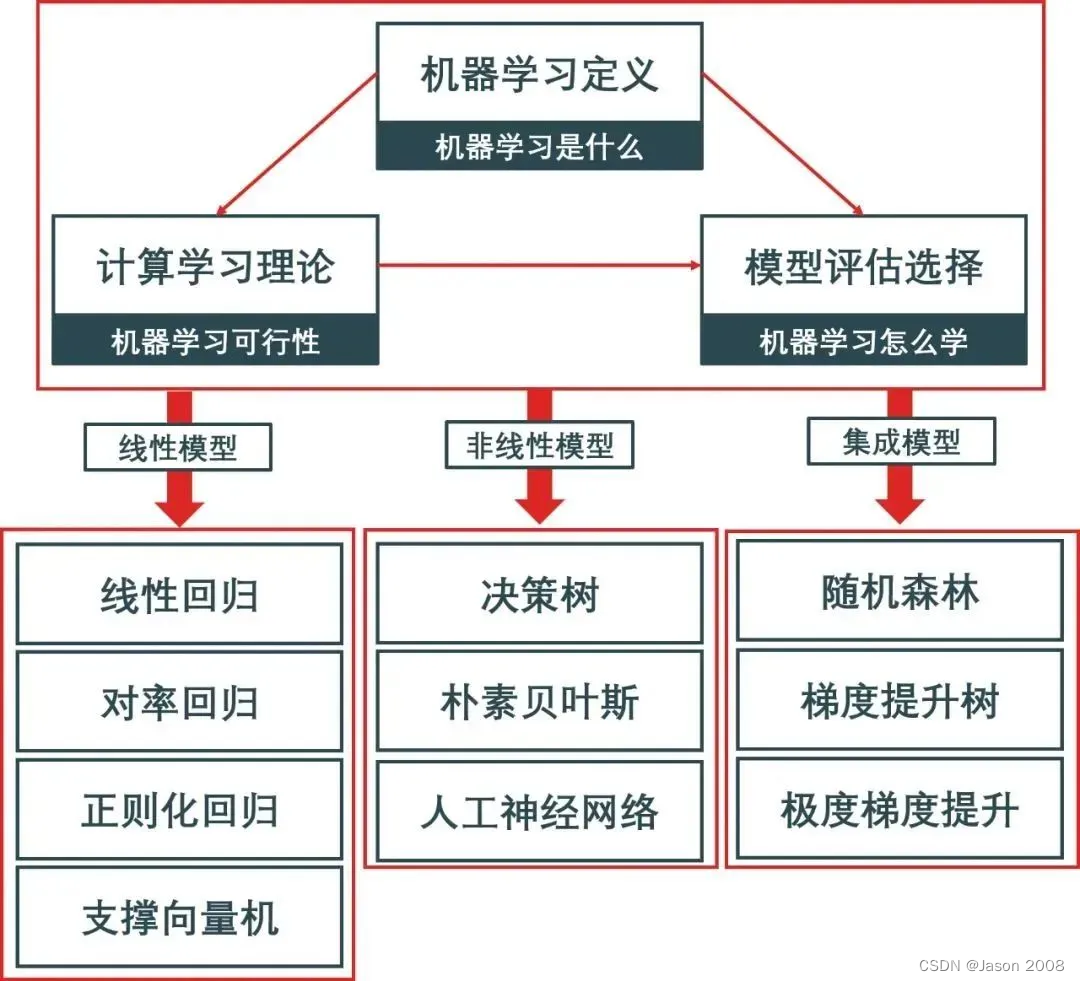
002-基于Sklearn的机器学习入门:基本概念
本节将继续介绍与机器学习有关的一些基本概念,包括机器学习的分类,性能指标等。同样,如果你对本节内容很熟悉,可直接跳过。 2.1 机器学习概述 2.1.1 什么是机器学习 常见的监督学习方法 2.1.2 机器学习的分类 机器学习一般包括监…...

ubuntu 默认的PATH配置
ubuntu 默认的PATH配置 在Ubuntu系统中,PATH环境变量是非常关键的,因为它定义了操作系统在接收到用户输入命令时,搜索可执行文件的目录顺序。这个变量的配置决定了哪些命令可以被系统全局识别和执行。 默认的PATH配置 Ubuntu的默认PATH环境…...
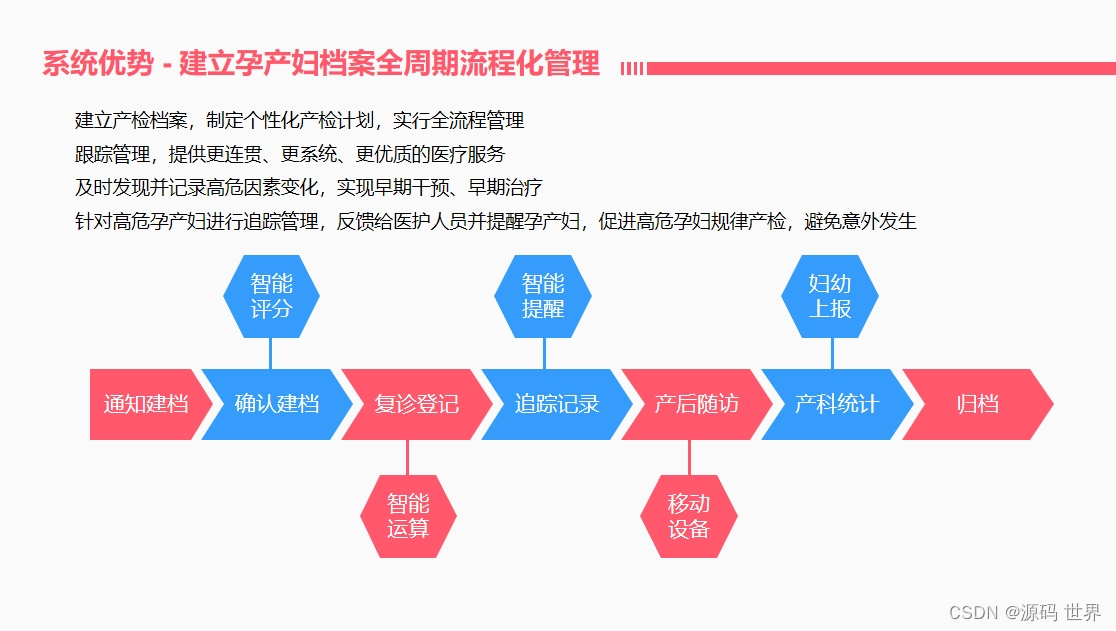
JAVA妇产科专科电子病历系统源码,前端框架:Vue,ElementUI
JAVA妇产科专科电子病历系统源码,前端框架:Vue,ElementUI孕产妇健康管理信息管理系统是一种将孕产妇健康管理信息进行集中管理和存储的系统。通过建立该系统,有助于提高孕产妇健康管理的效率和质量,减少医疗事故发生的…...

代码随想录算法训练营Day56|所有可达路径、797.所有可能的路径
所有可达路径 98. 所有可达路径 (kamacoder.com) 深度优先搜索,和之前的回溯题类似。 #include <iostream> #include <vector> using namespace std;// 定义一个二维向量来存储所有可能的路径 vector<vector<int>> paths; // 定义一个向…...
DNF手游鬼剑士攻略:全面解析流光星陨刀的获取与升级!云手机强力辅助!
《地下城与勇士》(DNF)手游是一款广受欢迎的多人在线角色扮演游戏,其中鬼剑士作为一个经典职业,因其强大的输出能力和炫酷的技能特效,吸引了众多玩家的青睐。在这篇攻略中,我们将详细介绍鬼剑士的一把重要武…...
npm创建一个空的vue3项目的方法或者pnpm创建vue3项目
1、前提我们已经安装了npm,或者pnpm 2、我们用npm来创建vue3项目 快速上手 | Vue.js 官网地址 这里我安装是的 node v18.20.3 以下是安装过程 : npm create vuelatest 根据自己的需要进行创建即可。 3、我们用pnpm来创建vite vue3项目 pnpm create …...
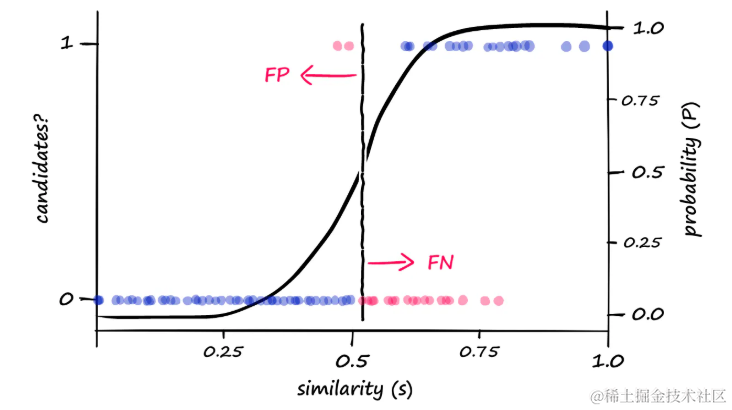
LSH算法:高效相似性搜索的原理与Python实现I
局部敏感哈希(LSH)技术是快速近似最近邻(ANN)搜索中的一个关键方法,广泛应用于实现高效且准确的相似性搜索。这项技术对于许多全球知名的大型科技公司来说是不可或缺的,包括谷歌、Netflix、亚马逊、Spotify…...

cesium 添加 Echarts图层(人口迁徒图)
cesium 添加 Echarts 人口迁徒图(下面附有源码) 1、实现思路 1、在scene上面新增一个canvas画布 2、通坐标转换,将经纬度坐标转为屏幕坐标来实现 3、将ecarts 中每个series数组中元素都加 coordinateSystem: ‘cesiumEcharts’ 2、示例代码 <!DOCTYPE html> <ht…...

Windows下快速安装Open3D-0.18.0(python版本)详细教程
目录 一、Open3D简介 1.1主要用途 1.2应用领域 二、安装Open3D 2.1 激活环境 2.2 安装open3d 2.3测试安装是否成功 三、测试代码 3.1 代码 3.2 显示效果 一、Open3D简介 Open3D 是一个强大的开源库,专门用于处理和可视化3D数据,如点云、网格和…...
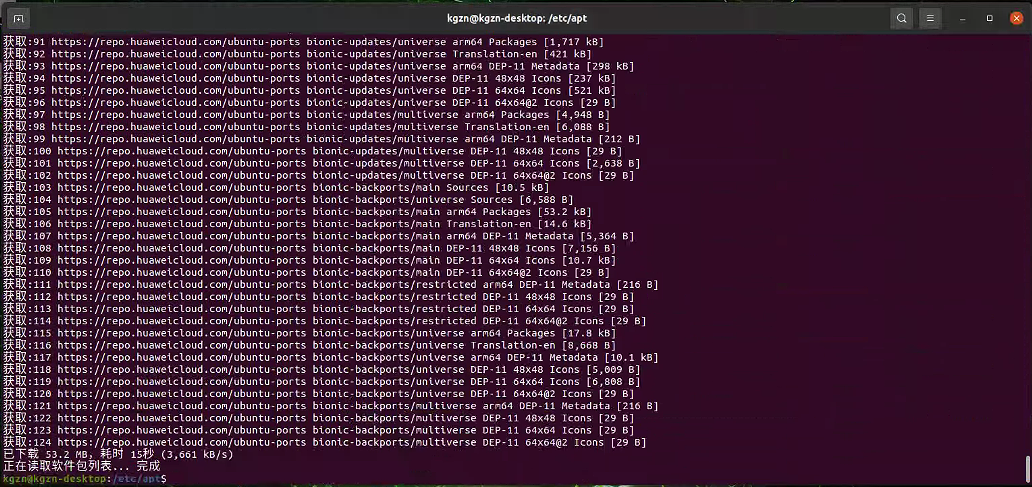
无法下载 https://mirrors./ubuntu/dists/bionic/main/binary-arm64/Packages
ubuntu系统执行sudo apt update命令的时候,遇到如下问题: 忽略:82 https://mirrors.tuna.tsinghua.edu.cn/ubuntu bionic-backports/universe arm64 Packages 错误:81 https://mirrors.tuna.tsinghua.edu.cn/ubuntu bionic-backports/main arm64 Packa…...
最新CRMEB商城多商户java版源码v1.6版本+前端uniapp
CRMEB 开源商城系统Java版,基于JavaVueUni-app开发,在微信公众号、小程序、H5移动端都能使用,代码全开源无加密,独立部署,二开很方便,还支持免费商用,能满足企业新零售、分销推广、拼团、砍价、…...
【开发环境】MacBook M2安装git并拉取gitlab项目,解决gitlab出现Access Token使用无效的方法
文章目录 安装Homebrew安装git打开IDEA配置git打开IDEA拉取项目 安装Homebrew /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)"在iTerm等命令行工具打开后,输入上面的命令 之后根据中文提示完成Homebrew的下载…...

Flask-Session使用Redis
Flask-Session使用Redis 一、介绍 在Flask中,session数据默认是以加密的cookie形式存储在用户的浏览器中的。但是,真正的session数据应该存储在服务器端。Django框架会将session数据存储在数据库的djangosession表中,而Flask则可以通过第三…...
Redis缓存管理机制
在当今快节奏的数字世界中,性能优化对于提供无缝的用户体验至关重要。缓存在提高应用程序性能方面发挥着至关重要的作用,它通过将经常使用或处理的数据存储在临时高速存储中来减少数据库负载并缩短响应时间,从而减少系统的延迟。Redis 是一种…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
