当前位置： 首页 > news >正文

PCL 点云聚类（基于体素连通性）

news 2025/11/2 19:52:04

文章目录

  • 一、简介
  • 二、实现代码
  • 三、实现效果
  • 参考资料

一、简介

这里的思路很简单，我们通过将点云转换为体素，基于体素的连通性实现对点云的聚类（有点类似于欧式聚类），不过这种方式进行的聚类有些粗糙，但聚类速度相对会快很多，具体的实现效果可以详细阅读代码。

二、实现代码

PointCloudVoxelCluster.h

#pragma once#include <iostream>
#include <vector>
#

相关文章：

PCL 点云聚类（基于体素连通性）

文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 这里的思路很简单，我们通过将点云转换为体素，基于体素的连通性实现对点云的聚类（有点类似于欧式聚类），不过这种方式进行的聚类有些粗糙，但聚类速度相对会快很多，具体的实现效果可以详细阅读代码。 二、实现代…...

编程日记 2024/7/3 6:18:51

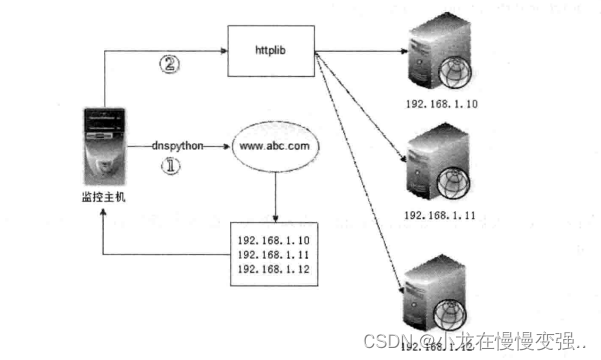
python自动化运维--DNS处理模块dnspython

1.dnspython介绍 dnspython是Pyhton实现的一个DNS工具包&#xff0c;他几乎支持所有的记录类型&#xff0c;可以用于查询、传输并动态更新ZONE信息&#xff0c;同事支持TSIG&#xff08;事物签名&#xff09;验证消息和EDNS0&#xff08;扩展DNS&#xff09;。在系统管理方面&a…...

编程日记 2024/7/3 6:17:50

成人职场商务英语学习柯桥外语学校|邮件中的“备注”用英语怎么说？

在英语中&#xff0c;"备注"通常可以翻译为"Notes" 或 "Remarks"。 这两个词在邮件中都很常用。例如: 1. Notes Notes: 是最通用和最常见的表达&#xff0c;可以用在各种情况下&#xff0c;例如&#xff1a; 提供有关电子邮件内容的附加信息 列…...

编程日记 2024/7/3 6:16:48

AndroidStudio报错macMissing essential plugin

电脑重启后打开studio&#xff1a; Missing essential plugin: org.jetbrains.android Please reinstall Android Studio from scratch. 无法使用 对应Mac下disabled_plugins.txt位于如下目录&#xff1a; /Users/ACB/Library/Application Support/Google/AndroidStudio4.2 …...

编程日记 2024/7/3 6:12:44

doris集群物理部署保姆级教程

doris物理安装 1、安装要求 Linux 操作系统版本需求​ 查看CentOs版本(>7.1) cat /etc/redhat-release 1&#xff09;设置系统最大打开文件句柄数​ vi /etc/security/limits.conf soft nofile 65536hard nofile 65536 echo ‘’’ soft nofile 655360hard nofile 655…...

编程日记 2024/7/3 6:09:42

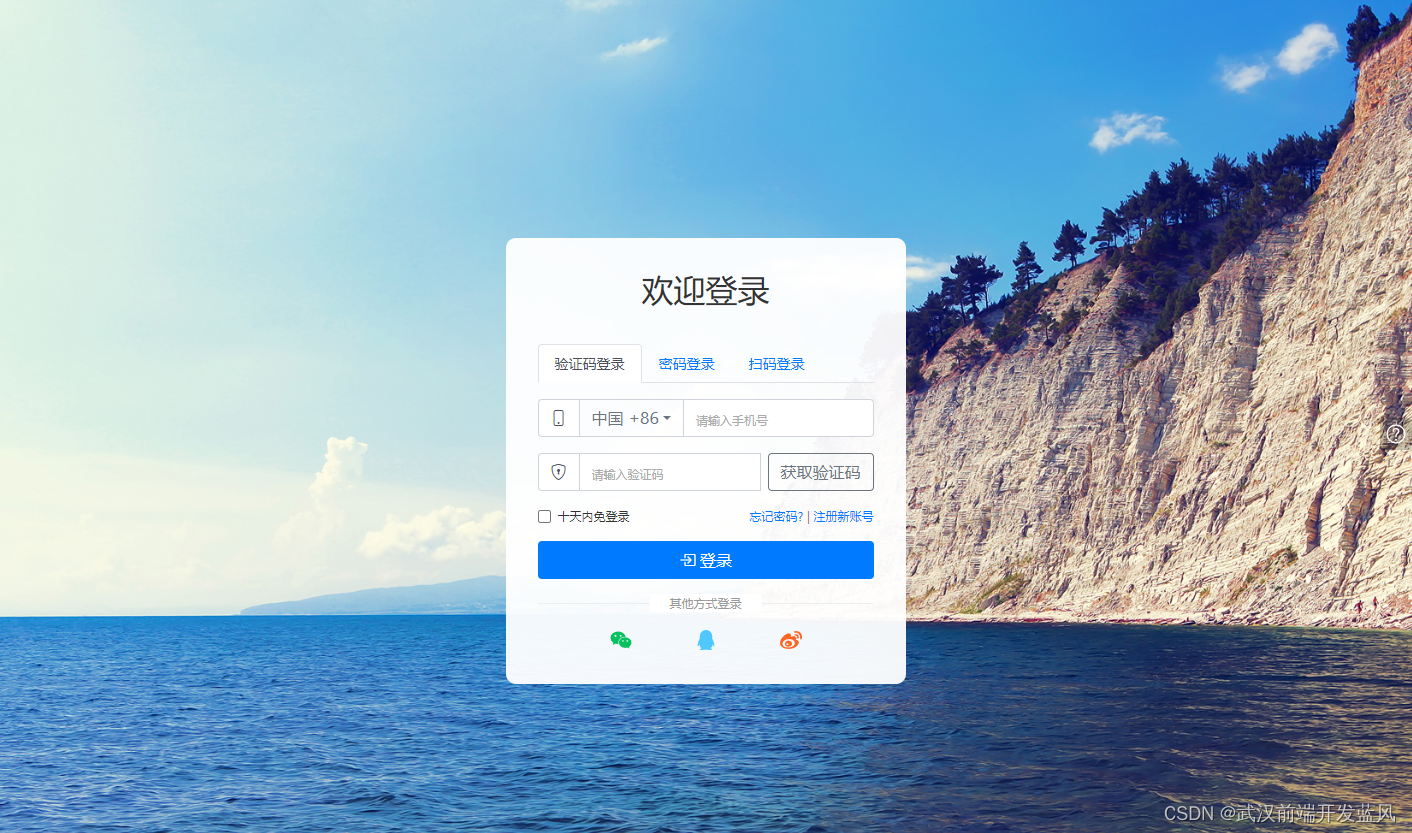
探囊取物之多形式登录页面(基于BootStrap4)

基于BootStrap4的登录页面&#xff0c;支持手机验证码登录、账号密码登录、二维码登录、其它统一登录 低配置云服务器&#xff0c;首次加载速度较慢&#xff0c;请耐心等候&#xff1b;演练页面可点击查看源码 预览页面&#xff1a;http://www.daelui.com/#/tigerlair/saas/pr…...

编程日记 2024/7/3 6:07:40

【ONLYOFFICE】| 桌面编辑器从0-1使用初体验

目录 一. &#x1f981; 写在前面二. &#x1f981; 在线使用感受2.1 创建 ONLYOFFICE 账号2.2 编辑pdf文档2.3 pdf直接创建表格 三. &#x1f981; 写在最后 一. &#x1f981; 写在前面 所谓桌面编辑器就是一种用于编辑文本、图像、视频等多种自媒体的软件工具&#xff0c;具…...

编程日记 2024/7/3 6:05:38

20、PHP字符串的排列（含源码）

题目&#xff1a; PHP字符串的排列&#xff1f; 描述&#xff1a; 输入一个字符串,按字典序打印出该字符串中字符的所有排列。 例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。 输入描述&#xff1a; 输入一个字符串,长度不超过9(可…...

编程日记 2024/7/3 6:03:35

Linux 标准IO的fopen和fclose

getchar(),putchar() ‐‐‐‐ 一个字符 gets(buf),puts(buf) ‐‐‐‐ 一串字符 scanf(),printf() ‐‐‐‐ 一个字符&#xff0c;一串字符都可以 fopen函数的形式 FILE * fopen(constchar *path , cost char *mode) /* * description : 打开一个文件 * param ‐ path…...

编程日记 2024/7/3 6:02:34

一个计算密集小程序在不同CPU下的表现

本文比较了几款CPU对同一测试程序的比较结果&#xff0c;用的是Oracle公有云OCI上的计算实例&#xff0c;均分配的1 OCPU&#xff0c;内存用的默认值&#xff0c;不过内存对此测试程序运行结果不重要。 本文只列结果&#xff0c;不做任何评价。下表中&#xff0c;最后一列为测…...

编程日记 2024/7/3 6:01:33

圈子系统搭建教程，以及圈子系统的功能特点，圈子系统，允许二开，免费源码，APP小程序H5

圈子是一款社区与群组的交友工具。你可以在软件内创造一个兴趣的群组从而达到按圈子来交友的效果用户可以根据自己的兴趣爱好。 1. 创建圈子 轻松创建专属圈子&#xff0c;支持付费型社群。 2. 加入圈子 加入不同圈子&#xff0c;设置不同名片&#xff0c;保护隐私。 3. 定…...

编程日记 2024/7/3 6:00:32

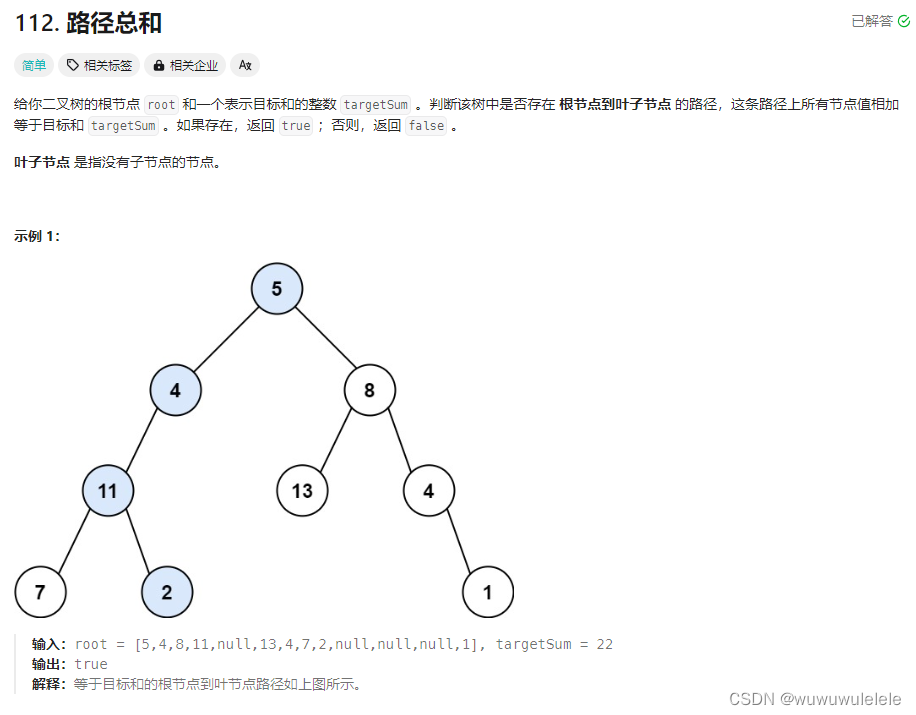
递归算法练习

112. 路径总和 package Tree;import java.util.HashMap; import java.util.Map;class TreeNode {int val;TreeNode left;TreeNode right;public TreeNode(int val) {this.val val;} }/*** 求 树的路径和* <p>* 递归 递减* <p>* 询问是否存在从*当前节点 root 到叶…...

编程日记 2024/7/3 5:59:31

WebDriver 类的常用属性和方法

目录 &#x1f38d;简介 &#x1f38a;WebDriver 核心概念 &#x1f389;WebDriver 常用属性 &#x1f381;WebDriver 常用方法 &#x1f437;示例代码 &#x1f3aa;注意事项 &#x1f390;结语 &#x1f9e3;参考资料 &#x1f38d;简介 Selenium WebDriver 是一个用…...

编程日记 2024/7/3 5:58:30

基于x86+FPGA+AI轴承缺陷视觉检测系统，摇枕弹簧智能检测系统

一、承缺陷视觉检测系统 应用场景 轴类零件自动检测设备&#xff0c;集光、机、软件、硬件&#xff0c;智能图像处理等先进技术于一体&#xff0c;利用轮廓特征匹配&#xff0c;目标与定位&#xff0c;区域选取&#xff0c;边缘提取&#xff0c;模糊运算等算法实现人工智能高…...

编程日记 2024/7/3 5:57:28

短剧小程序系统ｃｐｓ分销开发搭建

短剧小程序系统CPS分销开发搭建是一个相对复杂但具有广阔商业前景的过程。以下是关于短剧小程序系统CPS分销开发搭建的详细步骤和要点&#xff1a; 需求分析与市场调研&#xff1a; 深入了解市场需求、用户画像和竞品分析&#xff0c;明确产品定位和功能需求。研究目标用户的消…...

编程日记 2024/7/3 5:55:27

代理IP的10大误区：区分事实与虚构

在当今的数字时代&#xff0c;代理已成为在线环境不可或缺的一部分。它们的用途广泛&#xff0c;从增强在线隐私到绕过地理限制。然而&#xff0c;尽管代理无处不在&#xff0c;但仍存在许多围绕代理的误解。在本博客中&#xff0c;我们将探讨和消除一些最常见的代理误解&#…...

编程日记 2024/7/3 5:53:25

数组-长度最小的子数组

M长度最小的子数组&#xff08;leetcode209&#xff09; /*** param {number} target* param {number[]} nums* return {number}*/ var minSubArrayLen function(target, nums) {const n nums.length;let ans n 1;let sum 0; // 子数组元素和let left 0; // 子数组…...

编程日记 2024/7/3 5:51:23

深度学习之交叉验证

交叉验证&#xff08;Cross-Validation&#xff09;是一种用于评估和验证机器学习模型性能的技术&#xff0c;尤其是在数据量有限的情况下。它通过将数据集分成多个子集&#xff0c;反复训练和测试模型&#xff0c;以更稳定和可靠地估计模型的泛化能力。常见的交叉验证方法有以…...

编程日记 2024/7/3 5:50:22

使用 Python 五年后，我发现学 python 必看这三本书！少走一半弯路

第一本 《Python编程-从入门到实践》 适合零基础的读者 豆瓣评分&#xff1a;9.1 推荐指数&#xff1a;5颗星 推荐理由&#xff1a; 本书是针对所有层次的 Python 读者而作的 Python 入门书。全书分为两部分&#xff1a; 第一部分介绍使用Python 编程所必须了解的…...

编程日记 2024/7/3 5:49:21

React@16.x（45）路由v5.x（10）源码（2）- history

目录 1&#xff0c;作用1.1&#xff0c;createBrowserHistory1.2&#xff0c;createHashHistory1.3&#xff0c;createMemoryHistory 2&#xff0c;history 对象的属性2.1&#xff0c;action2.2&#xff0c;push / replace / go / goBack / goForward2.3&#xff0c;location2.…...

编程日记 2024/7/3 5:48:20

AI-调查研究-01-正念冥想有用吗？对健康的影响及科学指南

点一下关注吧&#xff01;&#xff01;&#xff01;非常感谢&#xff01;&#xff01;持续更新&#xff01;&#xff01;&#xff01; &#x1f680; AI篇持续更新中&#xff01;&#xff08;长期更新&#xff09; 目前2025年06月05日更新到&#xff1a; AI炼丹日志-28 - Aud…...

编程新知 2025/10/30 10:46:53

shell脚本--常见案例

1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件&#xff1a; 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

编程新知 2025/10/31 18:32:29

【网络安全产品大调研系列】2. 体验漏洞扫描

前言 2023 年漏洞扫描服务市场规模预计为 3.06&#xff08;十亿美元&#xff09;。漏洞扫描服务市场行业预计将从 2024 年的 3.48&#xff08;十亿美元&#xff09;增长到 2032 年的 9.54&#xff08;十亿美元&#xff09;。预测期内漏洞扫描服务市场 CAGR&#xff08;增长率&…...

编程新知 2025/10/31 15:37:22

YSYX学习记录（八）

C语言&#xff0c;练习0&#xff1a; 先创建一个文件夹&#xff0c;我用的是物理机&#xff1a; 安装build-essential 练习1&#xff1a; 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件&#xff0c;随机修改或删除一部分&#xff0c;之后…...

编程新知 2025/10/31 22:25:57

【2025年】解决Burpsuite抓不到https包的问题

环境&#xff1a;windows11 burpsuite:2025.5 在抓取https网站时&#xff0c;burpsuite抓取不到https数据包&#xff0c;只显示&#xff1a; 解决该问题只需如下三个步骤&#xff1a; 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

编程新知 2025/10/27 11:02:59

TRS收益互换：跨境资本流动的金融创新工具与系统化解决方案

一、TRS收益互换的本质与业务逻辑 &#xff08;一&#xff09;概念解析 TRS&#xff08;Total Return Swap&#xff09;收益互换是一种金融衍生工具&#xff0c;指交易双方约定在未来一定期限内&#xff0c;基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

编程新知 2025/11/2 0:31:23

C++中string流知识详解和示例

一、概览与类体系 C 提供三种基于内存字符串的流&#xff0c;定义在 <sstream> 中&#xff1a; std::istringstream&#xff1a;输入流&#xff0c;从已有字符串中读取并解析。std::ostringstream&#xff1a;输出流&#xff0c;向内部缓冲区写入内容&#xff0c;最终取…...

编程新知 2025/10/18 0:50:34

Linux离线（zip方式）安装docker

目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1&#xff1a;修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本&#xff1a;CentOS 7 64位 内核版本&#xff1a;3.10.0 相关命令&#xff1a; uname -rcat /etc/os-rele…...

编程新知 2025/6/16 16:58:04

JVM虚拟机：内存结构、垃圾回收、性能优化

1、JVM虚拟机的简介 Java 虚拟机（Java Virtual Machine 简称：JVM）是运行所有 Java 程序的抽象计算机，是 Java 语言的运行环境，实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息，使得 Java 程序只需生成在 JVM 上运行的目标代码（字节码），就可以…...

编程新知 2025/10/25 18:03:18

MFC 抛体运动模拟：常见问题解决与界面美化

在 MFC 中开发抛体运动模拟程序时，我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点，详细解析原因并提供解决方案，同时兼顾界面美化，让模拟效果更专业、更高效。 问题一：历史轨迹与小球残影残留 现象 小球运动后，历史位置的 “残影”…...

编程新知 2025/10/29 3:16:46