一篇文章入门主成分分析PCA
文章目录
- 基本概念
- 事件
- 随机变量
- 独立同分布
- 离散型随机变量
- 伯努利分布(两点分布)
- 二项分布
- 几何分布
- 泊松分布
- 连续型随机变量
- 正态分布
- 期望
- 方差
- 标准化
- 协方差
- 相关系数
- 线性组合
- 特征值和特征向量
- 特征值分解
- 对称矩阵的特征值分解
- 齐次线性方程组
- 单位向量
- 基向量
- 矩阵的秩
- 最高阶非零子式
- 正定矩阵
- 正交矩阵
- 正交基
- 逆矩阵
- 伴随矩阵
- 奇异值分解
- 主成分分析
基本概念
事件
事件:某种情况的“陈述” ⇒ \Rightarrow ⇒ 事件A:掷出的骰子为偶数点 ⇒ \Rightarrow ⇒ 事件A包含多种结果,每种结果都是一个基本事件 ⇒ \Rightarrow ⇒ 事件的本质是集合
事件之间的基本关系:
- 蕴含与相等:如果当A发生时B必发生 ,记数学公式: A ⊂ B A \subset B A⊂B数学公式: ⇒ \Rightarrow ⇒当数学公式: A , B A,B A,B相互蕴含时,两式相等,记数学公式: A = B A=B A=B
- 互斥与对立:在一次试验中不可能同时发生,但可以都不发生,有A就没有B,有B没有A,但是可以同时没有A和B数学公式: ⇒ \Rightarrow ⇒A为一事件,则事件 B={A不发生} ,则A和B互为对立事件
- 事件和(或称并集):A和B中至少发生一个(并集),记数学公式: C = A + B C=A+B C=A+B
- 事件积(或称交集):A发生且B发生(交集),记数学公式: C = A B C=AB C=AB
- 事件差:A发生且B不发生,记数学公式: C = A − B C=A-B C=A−B
全概率公式:一个事件的概率,该事件可以表示为若干互斥事件的联合

随机变量
随机变量是实验结果的函数 ⇒ \Rightarrow ⇒抛一枚硬币,定义1=正面朝上 ,0=反面朝上,所以随机变量 X X X就代表抛硬币这个试验的结果,要么0要么1
独立同分布
独立性:一个随机变量的取值不会影响另一个随机变量的取值
同分布:所有随机变量服从相同的概率分布
离散型随机变量
伯努利分布(两点分布)
伯努利分布:两种可能结果的实验(如成功和失败),成功的概率为 p p p,失败的概率为 1 − p 1-p 1−p
概率密度函数: P ( X = x ) = { p if x = 1 1 − p if x = 0 P(X=x)=\begin{cases}p&\text{if}\ \ x=1\\1-p&\text{if}\ \ x=0\end{cases} P(X=x)={p1−pif x=1if x=0
期望值: E ( X ) = p E(X)=p E(X)=p
方差: V a r ( X ) = p ( 1 − p ) Var(X)=p(1-p) Var(X)=p(1−p)
二项分布
二项分布:n次独立同分布的伯努利试验的成功次数的分布,每次试验成功的概率为 p p p 概率密度函数: P ( X = k ) = ( n k ) p k ( 1 − p ) n − k P(X=k)=\binom{n}kp^k(1-p)^{n-k} P(X=k)=(kn)pk(1−p)n−k
期望值: E ( X ) = n p E(X)=np E(X)=np
方差: V a r ( X ) = n p ( 1 − p ) Var(X)=np(1-p) Var(X)=np(1−p)
几何分布
几何分布:在第一次成功之前的失败次数(包括第一次成功),每次试验成功的概率为 p p p
概率密度函数: P ( X = k ) = ( 1 − p ) k p for k = 0 , 1 , 2 , … P(X=k)=(1-p)^kp\quad\text{for}\ \ k=0,1,2,\ldots P(X=k)=(1−p)kpfor k=0,1,2,…
期望值: E ( X ) = 1 − p p E(X)=\frac{1-p}p E(X)=p1−p
方差: Var ( X ) = 1 − p p 2 \operatorname{Var}(X)=\frac{1-p}{p^2} Var(X)=p21−p
泊松分布
泊松分布:单位时间或空间内某事件的发生次数,在一个间隔中平均发生事件的次数由 λ \lambda λ决定, λ \lambda λ是事件发生比率
概率密度函数: P ( X = k ) = λ k e − λ k ! P(X=k)=\frac{\lambda^ke^{-\lambda}}{k!} P(X=k)=k!λke−λ
期望值: E ( X ) = λ E(X)=\lambda E(X)=λ
方差: Var ( X ) = λ \operatorname{Var}(X)=\lambda Var(X)=λ
“事件”可理解为一天中网站的访客数、一天中所接到的电话数
例如:每周平均有15个人给我的博客点赞,我想预测下一周的点赞数
如果使用二项分布来解决,令 x x x表示在 n n n次重复实验中发生点赞的次数, p p p表示每次实验的点赞概率(Probability)。我们现在已知的是每周平均的点赞比率(rate)为15个赞/周,并不知道点赞概率 p p p和博客访客数 n n n的任何信息
假设过去的1年(=52周)的数据中,一共有 10000 10000 10000人看了我的博客,其中有 800 800 800个人点赞了,这样平均每周访客数 = 10000 / 52 = 192 =10000 / 52 = 192 =10000/52=192,平均每周点赞数 = 800 / 52 = 15 =800 / 52 = 15 =800/52=15,可得到概率 p = 800 / 10000 = 0.08 = 8 % p = 800 / 10000 = 0.08 = 8 \% p=800/10000=0.08=8%
使用二项分布的概率密度函数,预测下一周有20个人点赞的概率为: B i n ( m = 20 ∣ N = 192 , p = 0.08 ) = N ! ( N − m ) ! m ! p m ( 1 − p ) N − m = 0.04657 \mathrm{Bin(m=20\mid N=192,p=0.08)=\frac{N!}{(N-m)!m!}p^m(1-p)^{N-m}=0.04657} Bin(m=20∣N=192,p=0.08)=(N−m)!m!N!pm(1−p)N−m=0.04657
在上述过程中,可以将x=该周有15次点赞,也可以是x=该天有 15 / 7 = 2.1 15/7=2.1 15/7=2.1个赞,也可以是x=该小时有 15 / 7 ∗ 24 = 0.1 15/7*24=0.1 15/7∗24=0.1个赞,这意味着大多数小时没有赞,而有的小时有一个点赞。仔细想想,似乎一定时间内出现超过1个点赞的情况也是合理的(比如文章早上刚发布的时候)。由此,二项分布的问题是它无法在一个时间单元中包含超过1次的事件(在这里,时间单元是1小时)
那么,我们将1小时切分成60分钟,时间单元是1分钟,使得1小时能够包含多个事件。问题得到解决了吗?还没有,比如何同学的5G视频,一晚上点赞就过百万,1分钟内不止一个赞。那我们再将时间单元切分成秒,这样1分钟又能包含多个事件。这样思考下去,我们会将已有的事件单元不断地切分,直到满足一个时间单元只包含一个事件,而大的时间单元能够包含1个以上的事件
形式化来看,这意味着 n → ∞ n\to \infty n→∞,当我们假定比率(rate)固定,则必须让 p → 0 p\to 0 p→0,否则点赞数 n × p → ∞ n \times p \to \infty n×p→∞
基于以上的约束,时间单元变得无穷小。我们不用担心同一个时间单元包含一个以上的事件了
在用二项分布时,无法直接用比率(rate)来计算点赞概率 p p p,而是需要 n n n和 p p p才能使用二项分布的概率密度函数,而泊松分布不需要知道 n n n和 p p p,它假定 n n n是一个无穷大的数,而 p p p是无穷小的数,泊松分布唯一参数是比率 λ \lambda λ。现实中,得知 n n n和 p p p得进行很多次实验,而短时间内,比率(rate)很容易得到(例如,在下午2点-4点,收到了4个点赞)


泊松分布的假设:每个时间单元的事件平均发生比率是常数
例如:博客的每小时平均点赞数不太可能服从泊松分布,而博客每个月的平均点赞数可近似看作是固定的。假如你的博客写的很好,被公众号转发推广了,那可能会有大批的读者来阅读,这种情况下的点赞数就不满足泊松分布了
泊松分布的适用条件:
- 事件独立性:事件的发生是相互独立的,例如,每个读者对文章的点赞行为不受其他读者行为的影响
- 事件发生概率相等:每个事件在单位时间或空间内发生的概率是相同的
- 单位时间或空间内事件的发生率固定:单位时间或空间内事件的平均发生次数( λ \lambda λ)是固定的
当博客被公众号转发推广后,会出现以下变化:
- 读者行为不再独立:由于公众号转发,读者可能会集中在某个时间段内大量访问博客,导致点赞行为之间不再独立。例如,一个读者点赞后,可能会引起更多读者来点赞,这种情况下点赞行为具有相关性
- 事件发生概率不再相等:在被转发推广的时段,点赞的概率可能会显著提高,导致某些时间段内的点赞率远高于平时
- 事件发生率不固定:被推广后,单位时间内的访问量和点赞量会显著增加,不再符合泊松分布所要求的固定事件发生率

连续型随机变量
正态分布
概率密度函数: f ( x ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 f(x)=\frac1{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ21e−2σ2(x−μ)2
期望值: E ( x ) = μ E(x)=\mu E(x)=μ
方差: Var ( X ) = σ 2 \operatorname{Var}(X)=\sigma^2 Var(X)=σ2
期望
期望是随机变量取值的平均,以概率为权重对随机变量进行加权求和
平均数是对一组已经观察到的样本进行统计的量
由于概率是频率随样本趋于无穷的极限,所以期望其实就是平均数随样本趋于无穷的极限,两者是通过大数定理联系起来的
- 离散型随机变量的期望值 E ( X ) \mathrm{E}(X) E(X): E ( X ) = ∑ i x i P ( X = x i ) \mathrm{E}(X)=\sum_ix_iP(X=x_i) E(X)=∑ixiP(X=xi)
- 连续型随机变量的期望值 E ( X ) \mathrm{E}(X) E(X): E ( X ) = ∫ − ∞ ∞ x f X ( x ) d x E(X)=\int_{-\infty}^\infty xf_X(x) dx E(X)=∫−∞∞xfX(x)dx
期望的性质:
- E ( X 1 + X 2 + ⋯ + X n ) = E ( X 1 ) + E ( X 2 ) + ⋯ + E ( X n ) \mathrm{E}\left(\mathrm{X}_1 +\mathrm{X}_2 + \cdots +\mathrm{X}_\mathrm{n}\right)=\mathrm{E}\left(\mathrm{X}_1 \right)+\mathrm{E}\left(\mathrm{X}_2 \right)+ \cdots+\mathrm{E}\left(\mathrm{X}_\mathrm{n} \right) E(X1+X2+⋯+Xn)=E(X1)+E(X2)+⋯+E(Xn)(无条件成立)
- E ( X 1 X 2 ⋯ X n ) = E ( X 1 ) E ( X 2 ) ⋯ E ( X n ) \mathrm{E}(X_1 X_2 \cdots X_n) = \mathrm{E}(X_1 ) \mathrm{E} (X_2 ) \cdots \mathrm{E} (X_n ) E(X1X2⋯Xn)=E(X1)E(X2)⋯E(Xn)(独立情况下成立)
方差
方差是用来衡量随机变量和其数学期望之间的偏离程度的量,方差越大,那么这一组数据的波动幅度也就越大
因为 X X X是随机的,所以偏离的量 X − E X X-EX X−EX本身也是随机的,为了避免正负相互抵消,对其取平方作为偏离量,很自然方差就是该偏离量的期望,定义为: V a r ( X ) = E ( X − E X ) 2 = E ( X 2 ) − ( E X ) 2 \mathrm{Var(X)=E(X-EX)^2=E\left(X^2\right)-(EX)^2} Var(X)=E(X−EX)2=E(X2)−(EX)2
假如给定一个含有 n n n个样本的集合,则方差计算为: σ 2 = ∑ i = 1 n ( X i − X ˉ ) 2 n − 1 \mathrm{\sigma^2=\frac{\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}{n-1}} σ2=n−1∑i=1n(Xi−Xˉ)2
之所以除以n-1而不是除以n,是因为我们是用样本去估计总体,除n-1才是统计学上的“无偏估计”,这样能使我们以较小的样本集更好的逼近总体的标准差
方差的性质:
- 常数的方差为 0 0 0
- 若 C C C为常数,则 V a r ( X + C ) = V a r ( X ) \mathrm{Var(X+C)=Var(X)} Var(X+C)=Var(X)
- 若 C C C为常数,则 V a r ( C X ) = C 2 V a r ( X ) \mathrm{Var(CX)=C^2Var(X)} Var(CX)=C2Var(X)
- 独立情况下, V a r ( X 1 + ⋯ + X n ) = V a r ( X 1 ) + ⋯ + V a r ( X n ) \mathrm{Var\left(X_1\right.+\cdots+X_n})=\mathrm{Var\left(X_1)\right.}+\cdots+\mathrm{Var\left(X_n\right)} Var(X1+⋯+Xn)=Var(X1)+⋯+Var(Xn)
标准化
标准化可以使每个样本的均值为0、标准差为1: x ′ = x − x ˉ σ \mathrm x'=\frac{\mathrm x-\bar{\mathrm x}}\sigma x′=σx−xˉ
协方差
协方差衡量两个随机变量之间的线性关系
对于两个随机变量 X X X和 Y Y Y,协方差的定义为 Cov ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] = E ( X Y ) − E ( X ) E ( Y ) \operatorname{Cov}(X,Y)=E\left[(X-E(X))(Y-E(Y))\right]=E(XY)-E(X)E(Y) Cov(X,Y)=E[(X−E(X))(Y−E(Y))]=E(XY)−E(X)E(Y)
- 正协方差:如果 Cov ( X , Y ) > 0 \operatorname{Cov}(X,Y)>0 Cov(X,Y)>0,则表明 X X X和 Y Y Y之间存在正的线性关系
- 负协方差:如果 Cov ( X , Y ) < 0 \operatorname{Cov}(X,Y)<0 Cov(X,Y)<0,则表明 X X X和 Y Y Y之间存在负的线性关系
- 零协方差:如果 Cov ( X , Y ) = 0 \operatorname{Cov}(X,Y)=0 Cov(X,Y)=0,则表明 X X X和 Y Y Y之间没有线性关系 ⇒ \Rightarrow ⇒零协方差并不意味着 X X X和 Y Y Y完全不相关,它们可能存在非线性的关系
假设数据矩阵 X X X的大小为 n × p n\times p n×p,其中 n n n是样本数, p p p是特征数, X X X的每一行代表一个样本,每一列代表一个特征
给定数据矩阵 X X X,协方差矩阵的计算公式为: Σ = 1 n − 1 X T X \Sigma=\frac{1}{n-1}X^TX Σ=n−11XTX
X T X X^TX XTX是一个 p × p p\times p p×p的矩阵,表示各特征之间的内积和

相关系数
协方差虽然能反映两个随机变量的相关程度,为了标准化这种相关性,我们通常使用相关系数(Correlation Coefficient),其定义为: ρ X , Y = Cov ( X , Y ) σ X σ Y E [ ( X − E X ) ( Y − E Y ) ] σ X σ Y = E ( X Y ) − E ( X ) E ( Y ) E ( X 2 ) − E 2 ( X ) E ( Y 2 ) − E 2 ( Y ) \rho_{X,Y}=\frac{\operatorname{Cov}(X,Y)}{\sigma_X\sigma_Y}\begin{aligned}\frac{\mathrm{E}\left[\left(\mathrm{X}-\mathrm{E}\mathrm{X}\right)\left(\mathrm{Y}-\mathrm{E}\mathrm{Y} \right)\right]}{\sigma_\mathrm{X} \sigma_\mathrm{Y}}&=\frac{\mathrm{E}\left(\mathrm{X}\mathrm{Y}\right)-\mathrm{E}\left(\mathrm{X}\right)\mathrm{E}\left(\mathrm{Y}\right)}{\sqrt{\mathrm{E}\left(\mathrm{X}^2\right)-\mathrm{E}^2\left(\mathrm{X}\right)}\sqrt{\mathrm{E}\left(\mathrm{Y}^2\right)-\mathrm{E}^2\left(\mathrm{Y}\right)}}\end{aligned} ρX,Y=σXσYCov(X,Y)σXσYE[(X−EX)(Y−EY)]=E(X2)−E2(X)E(Y2)−E2(Y)E(XY)−E(X)E(Y),其中 σ X \sigma_X σX和 σ Y \sigma_Y σY分别是 X X X和 Y Y Y的标准差,相关系数 ρ X , Y \rho_{X,Y} ρX,Y的值域为 [ − 1 , 1 ] [-1,1] [−1,1],值越接近 1 或 -1,表明 X X X和 Y Y Y之间的线性关系越强
线性组合
线性组合:设 β , α 1 , α 2 , . . . , α n \mathrm{\beta} , \alpha_{1} , \alpha_{2} , ..., \alpha_{\mathrm{n}} β,α1,α2,...,αn是一组 m m m维向量,若存在数 k 1 , k 2 , . . . , k n \mathrm{k_{1} , k_{2} , ...,k_{n}} k1,k2,...,kn,使得 β = k 1 α 1 + k 2 α 2 + . . . + k n α n \mathrm{\beta=k_1\alpha_1~+k_2\alpha_2~+~...~+k_n\alpha_n} β=k1α1 +k2α2 + ... +knαn,则称 β \beta β是向量组 α 1 , α 2 , . . . , α n \alpha_{1} , \alpha_{2} , ..., \alpha_{\mathrm{n}} α1,α2,...,αn的线性组合, k 1 , k 2 , . . . , k n \mathrm{k_{1} , k_{2} , ...,k_{n}} k1,k2,...,kn为一组组合系数
性质:
- 零向量可由任意向量组来线性表示: 0 = 0 α 1 + 0 α 2 + . . . + 0 α n \mathbf{0}=0\alpha_1+0\alpha_2+...+0\alpha_\mathrm{n} 0=0α1+0α2+...+0αn
- 向量组中任意一个向量可由向量组来线性表示: α 3 = 0 α 1 + 0 α 2 + 1 α 3 + 0 α 4 \alpha_3=0\alpha_1+0\alpha_2+1\alpha_3+0\alpha_4 α3=0α1+0α2+1α3+0α4
- 任意一个向量都可由基向量 ε 1 = ( 1 , 0 , . . . , 0 ) , ε 2 = ( 0 , 1 , . . . , 0 ) , . . . , ε n = ( 0 , 0 , . . . , 1 ) \begin{aligned}\varepsilon_1& =(1,0,...,0),\varepsilon_2 =(0,1,...,0),...,\varepsilon_\text{n} =(0,0,...,1)\end{aligned} ε1=(1,0,...,0),ε2=(0,1,...,0),...,εn=(0,0,...,1)来线性表示: ( 1 , 2 , 3 ) = 1 × ( 1 , 0 , 0 ) + 2 × ( 0 , 1 , 0 ) + 3 × ( 0 , 0 , 1 ) (1,2,3)=1\times(1,0,0)+2\times(0,1,0)+3\times(0,0,1) (1,2,3)=1×(1,0,0)+2×(0,1,0)+3×(0,0,1)
设 β = ( − 3 , 2 , − 4 ) , α 1 = ( 1 , 0 , 1 ) , α 2 = ( 2 , 1 , 0 ) , α 3 = ( − 1 , 1 , − 2 ) \beta = (-3,2,-4), \alpha_{1} = (1,0,1), \alpha_{2} = (2,1,0), \alpha_{3} =(-1,1,-2) β=(−3,2,−4),α1=(1,0,1),α2=(2,1,0),α3=(−1,1,−2),判断 β \beta β是否可由 α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α1,α2,α3线性表示?

特征值和特征向量
特征向量表示变换的方向,特征值表示在每个方向上的伸缩程度

特征值分解
相似矩阵:设 A , B A,B A,B都是 n n n阶矩阵,若有可逆矩阵 P P P,使 P − 1 A P = B \mathrm{P}^{-1}\mathrm{AP}=\mathrm{B} P−1AP=B,则称 A A A与 B B B相似,这个过程称为相似变换, P P P为相似变换矩阵
如果 A A A与对角矩阵 Λ = ( λ 1 λ 2 ⋱ λ n ) \left.\boldsymbol{\Lambda}=\left(\begin{array}{rrrrr}\lambda_{1}&&&&\\&\lambda_{2}&&&\\&&\ddots&&\\&&&\lambda_{\mathrm{n}}&\end{array}\right.\right) Λ= λ1λ2⋱λn 相似,即 P − 1 A P = Λ \mathrm{P}^{-1}\mathrm{AP}=\Lambda P−1AP=Λ,那么 λ 1 , λ 2 , ⋯ , λ n \lambda_{1},\lambda_{2} ,\cdots ,\lambda_{\mathrm{n}} λ1,λ2,⋯,λn是 A A A的 n n n个特征值,而 P P P的列向量 p i p_i pi就是 A A A对应于特征值 λ i \lambda_i λi的特征向量
把 P P P乘到右边,得到: A = P Λ P − 1 \mathrm A=\mathrm P\Lambda\mathrm P^{-1} A=PΛP−1这个式子就是实际中经常用到的特征值分解,一个矩阵 A A A可以通过特征值分解得到它的特征值和特征向量
对称矩阵的特征值分解
对称矩阵: A T = A \mathrm{A^{T}}=\mathrm{A} AT=A ⇒ \Rightarrow ⇒对称矩阵有 N N N个线性无关的特征向量,且不同特征值对应的特征向量相互正交
对称矩阵一定可以相似对角化,故实对称矩阵 A A A可以被分解成: A = P Λ P − 1 = P Λ P T \mathrm{A}=\mathrm{P} \Lambda\mathrm{P}^{-1}=\mathrm{P} \mathrm{\Lambda}\mathrm{P}^{\mathrm{T}} A=PΛP−1=PΛPT,其中 P P P为正交矩阵( P P T = E \mathrm{PP}^{\mathrm{T}}=\mathrm{E} PPT=E)
齐次线性方程组
齐次线性方程组是指所有常数项(即方程的右端)都等于零的线性方程组: A x = 0 A\mathbf{x}=\mathbf{0} Ax=0,其中 A A A是一个 m × n m\times n m×n的矩阵, x \mathbf{x} x是一个 n n n维列向量, 0 \mathbf{0} 0是一个 m m m维列向量

单位向量
单位向量是指长度为1的向量,在欧几里得空间中,如果向量 u \mathbf{u} u满足 ∥ u ∥ = 1 \|\mathbf{u}\|=1 ∥u∥=1,其中 ∥ u ∥ \|\mathbf{u}\| ∥u∥表示向量 u \mathbf{u} u的长度,则 u \mathbf{u} u是一个单位向量

基向量
基向量是向量空间的一组向量,通过线性组合这些向量可以表示空间中的任何向量,向量空间中的基向量通常是线性无关的
矩阵的秩
矩阵的秩(Rank)是其行向量的最大线性无关组的数量
从几何角度来看,矩阵的秩表示由矩阵的行向量生成的向量空间的维数,对于一个 3 × 3 3\times3 3×3的矩阵:
- 如果其秩为 3,表示其行向量是三维空间的基,可以生成整个三维空间
- 如果秩为 2,表示行向量位于同一平面,且可以生成一个二维平面
- 如果秩为 1,表示所有行向量都在同一条直线上

对于方阵,如果其行列式不为零,则该矩阵是满秩矩阵,即秩等于矩阵的阶数。反之,如果行列式为零,则矩阵的秩小于其阶数
最高阶非零子式
一个 k × k k\times k k×k子式是从矩阵中选取 k k k行和 k k k列形成的一个 k × k k\times k k×k方阵的行列式
最高阶非零子式是指在所有非零子式中,阶数最高的那个子式
假设有一个 3 × 3 3\times 3 3×3矩阵: A = ( 1 2 3 4 5 6 7 8 9 ) A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix} A= 147258369

正定矩阵
正定矩阵是一种特殊的实对称矩阵
实对称矩阵:矩阵的转置等于其自身的矩阵,对于任意 i i i和 j j j,其第 i i i行第 j j j列的元素等于第 j j j行第 i i i列的元素
一个实对称矩阵 A A A 被称为正定的,如果对于任意非零向量 x x x,都有 x T A x > 0 x^TAx>0 xTAx>0
一个实对称矩阵 A A A被称为半正定的,如果对于任意非零向量 x x x,都有 x T A x ≥ 0 x^TAx\geq0 xTAx≥0
正交矩阵
正交矩阵的逆矩阵和转置矩阵是相同的
一个正交矩阵 Q Q Q满足下列条件:
- 它是一个方阵(即行数等于列数)
- 它的每一列都是单位向量,并且相互正交
正交基
一个向量组 { u 1 , u 2 , … , u n } \{\mathbf{u}_1,\mathbf{u}_2,\ldots,\mathbf{u}_n\} {u1,u2,…,un}是正交基,如果组内的任意两个向量都是正交的,即 u i ⋅ u j = 0 \mathbf{u}_{i}\cdot\mathbf{u}_{j}=0 ui⋅uj=0(对于所有 i ≠ j i\neq j i=j),如果这些向量还都是单位向量,则称它们是正交规范基
在三维空间中,标准基向量 { e 1 , e 2 , e 3 } \{\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3\} {e1,e2,e3}是一个正交规范基: e 1 = ( 1 , 0 , 0 ) , e 2 = ( 0 , 1 , 0 ) , e 3 = ( 0 , 0 , 1 ) \mathbf{e}_1=(1,0,0),\quad\mathbf{e}_2=(0,1,0),\quad\mathbf{e}_3=(0,0,1) e1=(1,0,0),e2=(0,1,0),e3=(0,0,1)
逆矩阵
假如说,矩阵 A A A是逆时针旋转90°的变换,则 A − 1 A^{-1} A−1是顺时针旋转90°的变换
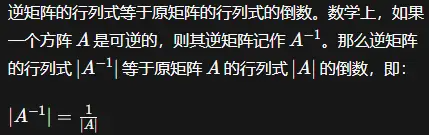
如果矩阵 A A A可逆,则 A − 1 = A ∗ ∣ ∣ A ∣ ∣ A^{-1}=\frac{A^{*}}{||A||} A−1=∣∣A∣∣A∗( ∣ ∣ A ∣ ∣ = det ( A ) ||A||=\det(A) ∣∣A∣∣=det(A),即矩阵的行列式)
伴随矩阵
伴随矩阵 A ∗ A^{*} A∗
余子式: A A A关于第 i i i行第 j j j列的余子式(记作 M i j M_{ij} Mij)是去掉 A A A的第 i i i行第 j j j列之后得到的 ( n − 1 ) × ( n − 1 ) (n-1)\times (n-1) (n−1)×(n−1)矩阵的行列式
代数余子式: A A A关于第 i i i行第 j j j列的代数余子式(记作 C i j C_{ij} Cij)为 ( − 1 ) i + j M i j (-1)^{i+j}M_{ij} (−1)i+jMij
余子矩阵: A A A的余子矩阵是一个 n × n n\times n n×n的矩阵 C C C,使得第 i i i行第 j j j列的元素是 A A A关于第 i i i行第 j j j列的代数余子式
伴随矩阵:矩阵 A A A的伴随矩阵是 A A A的余子矩阵的转置矩阵
奇异值分解
特征分解只适用于方阵,奇异值分解SVD适用于任意矩阵分解
从相似对角化的的定义可以看到,我们可以把一个复杂的矩阵 A A A变成一个很简单的对角矩阵,而这个对角矩阵也同样保留了原来矩阵的特征,且变换的矩阵 P P P就是 A A A的特征向量组成的矩阵
但是注意,不是每一个矩阵都能与对角矩阵相似,首先注意到 P P P必须是可逆的,而 P P P又是特征向量组成 ⇒ \Rightarrow ⇒当且仅当 A A A有 n n n个线性无关的特征向量时, A A A才能相似对角化
奇异值分解就像是把一个复杂的玩具分解成几个更简单的小玩具,然后用这些小玩具重新拼装成原来的玩具
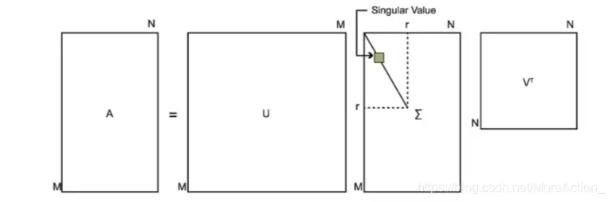
假设我们有一个 m × n m\times n m×n的矩阵 A A A,,奇异值分解把它分解成三个矩阵: A = U Σ V T A=U\Sigma V^{T} A=UΣVT
- 矩阵 U U U: m × m m\times m m×m的正交矩阵,其中的列向量 u 1 ⃗ , u 2 ⃗ , … , u m ⃗ \vec{\mathrm{u}_1},\vec{\mathrm{u}_2},\ldots,\vec{\mathrm{u}_m} u1,u2,…,um是 A A T AA^T AAT的特征向量,称为矩阵 A A A的左奇异向量
- 矩阵数学 Σ \Sigma Σ: m × n m\times n m×n的矩阵,除了主对角线上的元素以外全为0,主对角线上的元素 σ i \sigma_i σi称为奇异值, σ i = λ i \sigma_{\mathrm{i}}=\sqrt{\lambda_{\mathrm{i}}} σi=λi, λ i \lambda_i λi是 A A T AA^T AAT的特征值
- 矩阵 V T V^T VT: n × n n\times n n×n的正交矩阵,其中的列向量 v ⃗ 1 , v ⃗ 2 , … , v ⃗ m \vec{\mathrm{v}}_{1} , \vec{\mathrm{v}}_{2} ,\ldots, \vec{\mathrm{v}}_{\mathrm{m}} v1,v2,…,vm是 A T A A^TA ATA的特征向量,称为矩阵 A A A的右奇异向量
奇异值在矩阵中是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说,我们可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说: A m × n = U m × m Σ m × n V n × n T ≈ U m × k Σ k × k V k × n T \mathrm A_{\mathrm m\times\mathrm n}=\mathrm U_{\mathrm m\times\mathrm m}\Sigma_{\mathrm m\times\mathrm n}\mathrm V_{\mathrm n\times\mathrm n}^{\mathrm T}\approx\mathrm U_{\mathrm m\times\mathrm k}\Sigma_{\mathrm k\times\mathrm k}\mathrm V_{\mathrm k\times\mathrm n}^{\mathrm T} Am×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nT,其中,k是一个远小于m、n的数。SVD具有的这种特性可以用于PCA降维、数据压缩和去噪等
A A T AA^T AAT是对称矩阵

主成分分析
假设我们有一组二维数据 ( x , y ) (x,y) (x,y),它的分布如下:
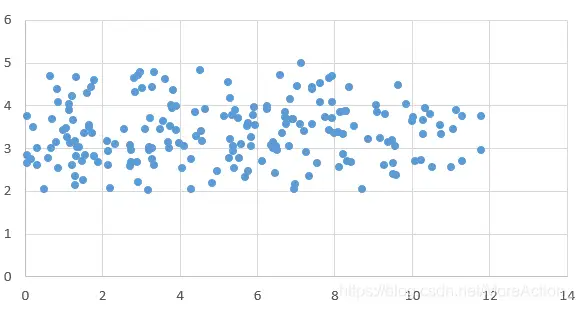
可以看到,数据在x轴上的变化大,而在y轴变化小,变化小意味着数据在这个特征上没有太大的差异,因此它包含的信息就比较少,那么我们就可以认为它是不重要的或者是噪音,从而可以直接将这个维度上的数据舍去,只用x轴上的数据来代替
那么假如数据是这样分布的呢?
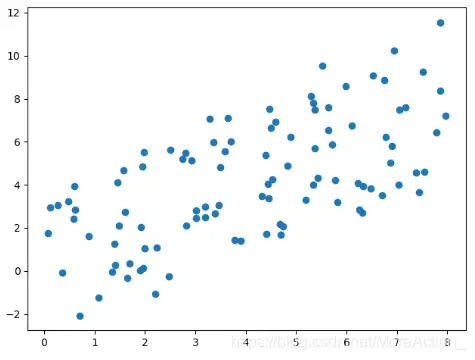
这个图我们就不太好看出到底是谁比较重要了,因为x和y变化都比较大,那么就不能降维了吗?非也,假如我们旋转一下坐标系
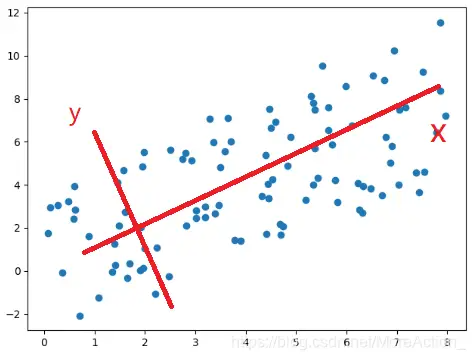
从这个例子也可以看到,数据本身的具体数值其实是不重要的,重要的是数据之间的关系,数据的整体分布。原来的数据是在 E E E坐标系下,然后我们换了一个坐标系来表示,本质上相当于对数据进行了一次正交变换(从数学公式看),在新的坐标系下,我们能更清楚的看到数据的特点
PCA的目标是将原始数据转换到一个新的坐标系中,这个新坐标系的轴(主成分)是数据方差最大的方向
主成分是在数据集中找到方差最大的方向(即主成分),然后将数据投影到这些方向上
方差最大化:每个主成分方向上数据的方差最大,这意味着这个方向上数据分布最广,包含最多的信息
正交性:不同主成分之间是相互正交的,即它们彼此垂直且不相关
PCA的步骤:
- 数据标准化:将每个特征的均值变为零,方差变为一,确保每个特征对主成分的贡献是均衡的 ⇒ \Rightarrow ⇒ 标准化数据 = X − μ σ \text{标准化数据}=\frac{X-\mu}\sigma 标准化数据=σX−μ
- 计算协方差矩阵:协方差矩阵描述了不同特征之间的线性关系 ⇒ \Rightarrow ⇒ Σ = 1 n − 1 X T X \Sigma=\frac{1}{n-1}X^TX Σ=n−11XTX,其中, Σ \Sigma Σ是协方差矩阵, X X X是标准化后的数据矩阵, n n n是样本数量
- 特征值分解:对协方差矩阵进行特征值分解,得到特征值和特征向量 ⇒ \Rightarrow ⇒ Σ = V Λ V T \Sigma=V\Lambda V^{T} Σ=VΛVT,其中, V V V是特征向量矩阵, Λ \Lambda Λ是对角矩阵,对角线上的元素是特征值
- 选择前 k k k个主成分:选择特征值最大的 k k k个特征向量,作为新的特征子空间的基,这些特征向量就是主成分;特征值代表了每个特征向量方向上的方差大小,特征值越大,表示这个方向上的方差越大,包含的信息越多
- 变换数据:用选择的 k k k个主成分对原始数据进行变换,得到降维后的数据 Y = X P Y=XP Y=XP,其中, Y Y Y是降维后的数据矩阵, P P P是由选择的 k k k个特征向量构成的矩阵

参考文献
1、ChatGPT3.5、ChatGPT4.0、ChatGPT4o
2、概率分布介绍—泊松分布:https://blog.csdn.net/weixin_44633882/article/details/120313676
3、相关系数——皮尔逊相关系数:https://blog.csdn.net/MoreAction_/article/details/106195689
4、《线性代数》教学视频 宋浩老师:https://www.bilibili.com/video/BV1aW411Q7x1?p=1&vd_source=8469f059ce75462e1674032ec0bfc23a
5、一文读懂特征值分解EVD与奇异值分解SVD:https://blog.csdn.net/MoreAction_/article/details/107318158
6、一文让你彻底搞懂主成成分分析PCA的原理及代码实现:https://blog.csdn.net/MoreAction_/article/details/107463336
相关文章:

一篇文章入门主成分分析PCA
文章目录 基本概念事件随机变量独立同分布离散型随机变量伯努利分布(两点分布)二项分布几何分布泊松分布 连续型随机变量正态分布 期望方差标准化协方差相关系数线性组合特征值和特征向量特征值分解对称矩阵的特征值分解 齐次线性方程组单位向量基向量矩…...

Android系统为什么lmkd杀到adj 100就代表有低内存?
在Android系统中,lmkd(Low Memory Killer Daemon,低内存终止守护进程)负责监控系统的内存状态,并在内存压力较高时通过终止不必要的进程来释放内存,以维持系统的稳定运行。关于lmkd为何在杀到adj࿰…...
)
d嘤嘤不想求异或喵(牛客周赛49)
题意: 嘤嘤有两个整数 l,r,她想知道区间 [l,r] 所有整数的异或和是多少. 分析: 样例1只有一个数输出1 样例2 1^201^10113 样例3 1^2^301^10^1111^11000 #include<bits/stdc.h> using namespace std; typedef long long ll; ll f(l…...

java反射-动态调用方法
通过字符串动态创建对象,通过字符串动态使用对象方法 package com.hmdp.service.动态调用方法;import java.lang.reflect.Method;public class Main {public static void main(String[] args) throws Exception {String name "javax.swing.JFrame";Clas…...

ThreadLocal作用
ThreadLocal作用(线程本地存储) ThreadLocal,很多地方叫做线程本地变量,也有些地方叫做线程本地存储,ThreadLocal的作用是提供线程内的局部变量,这种变量在线程的生命周期内起作用,减少同一个线程内多个函数或者组件之…...

Python基础入门知识
目录 引言 简要介绍Python语言 为什么要学习Python Python的应用领域 Python安装和环境配置 Python的下载和安装(Windows, macOS, Linux) 配置Python环境变量 安装和使用IDE(如PyCharm, VS Code) Python基本语法 注释 变量和数据类型(数字,字符串,列表,元组,字典,…...
uniapp——据用户角色显示或隐藏部分功能权限。
v-if"user.state.agent_level!business || (user.state.agent_levelbusiness && item.value ! 3 && item.value ! 4)"...
JCR一区级 | Matlab实现BO-Transformer-LSTM多变量回归预测
JCR一区级 | Matlab实现BO-Transformer-LSTM多变量回归预测 目录 JCR一区级 | Matlab实现BO-Transformer-LSTM多变量回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现BO-Transformer-LSTM多变量回归预测,贝叶斯优化Transformer结合LSTM长…...
)
软件开发环境-系统架构师(二十一)
1、对计算机评价的主要性能指标有时钟频率、()、运算精度和内存容量等。 对数据库管理系统评价的主要性能指标有()、数据库所允许索引数量和最大并发事务处理能力。 问题1 A丢包率 B端口吞吐量 C可移植性 D数据处理速率 问题…...

AI与大模型工程师证书研修班报名啦!
人工智能大模型是指拥有超大规模参数(通常在十亿个以上)、超强计算资源的机器学习模型,能够处理海量数据,完成各种复杂任务,如自然语言处理、图像识别等。计算机硬件性能不断提升,深度学习算法快速优化&…...
ctfshow-web入门-命令执行(web56、web57、web58)
目录 1、web56 2、web57 3、web58 1、web56 命令执行,需要严格的过滤 新增过滤数字,只能采用上一题临时文件上传的方法: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><…...
controller不同的后端路径对应vue前端传递数据发送请求的方式,vue请求参数 param 与data 如何对应后端参数
目录 案例一: 为什么使用post发送请求,参数依旧会被拼接带url上呢?这应该就是param 与data传参的区别。即param传参数参数会被拼接到url后,data会以请求体传递 补充:后端controller 参数上如果没写任何注解,…...

【FFmpeg】avcodec_send_frame函数
目录 1.avcodec_send_frame1.1 将输入的frame存入内部buffer(encode_send_frame_internal)1.1.1 frame的引用函数(av_frame_ref )1.1.1.1 帧属性的拷贝(frame_copy_props)1.1.1.2 buffer的引用函数…...

python获取字符编码
在Python中,您可以使用内置的ord()函数获取单个字符的Unicode编码,使用encode()方法获取字符串的字节编码。 获取单个字符的Unicode编码: char a unicode_code ord(char) print(unicode_code) # 输出字符的Unicode编码 获取字符串的字节编码: tex…...

通过MATLAB控制TI毫米波雷达的工作状态之实时数据采集
前言 前一章博主介绍了如何基于MATLAB的各种前面板组件结合MATLAB代码来发送CFG指令控制毫米波雷达的工作状态,这一章节博主将介绍如何基于这些组件结合MATLAB代码来实现TI毫米波雷达数据的实时采集。目前大部分TI毫米波雷达的数据采集均是仅可以采集一段数据又或者利用DAC10…...

华为HCIP Datacom H12-821 卷21
1.单选题 以下关于PIM-SM中SPT切换的描述,错误的是哪一项? A、若所有组播流量都经过RP路由器,则RP路由器可能成为数据转发的瓶颈 B、SPT路径最短,转发性能更优 C、SPT 切换完成后,组播流量依然经过 ReT 树 D、RPT 树可能不是组播流量转发的最优路径 正确答案: C 解析…...
MySQL之应用层优化(二)
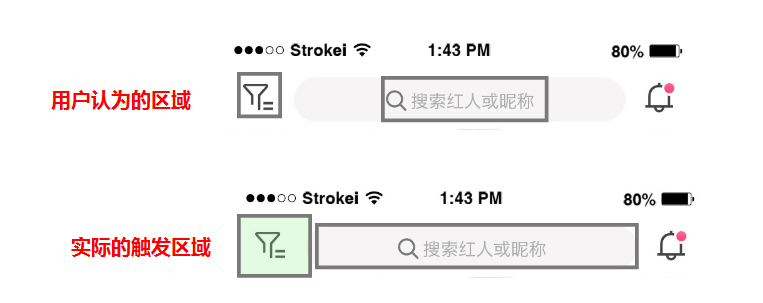
应用层优化 Web服务器问题 寻找最优并发度 每个Web服务器都有一个最佳并发度——就是说,让进程处理请求尽可能快,并且不超过系统负载的最优的并发连接数。这就是前面说的最大系统容量。进行一个简单的测量和建模,或者只是反复试验…...

Java源码解读之常量52429
文章目录 为什么有52429的常量呢?对于为什么选择52429?那么为什么不再选几位呢? 在JDK8源码中 java.lang.Integer有52429作为常量出现, 为什么有52429的常量呢? static void getChars(int i, int index, char[] buf) {int q, r;…...

“Photoshop AI插件:StartAI的全面使用攻略
随着人工智能技术的飞速发展,Photoshop作为设计师们不可或缺的工具,也在不断地融入AI技术,以提升设计效率和效果。在2024年,PSAI插件StartAI因其强大的功能和易用性,成为了Photoshop用户的得力帮手。下面来给大家详细介…...
入门Axure:快速掌握原型设计技能
2002 年,维克托和马丁在旧金山湾区的一家初创公司工作,发现自己一再被软件开发生命周期的限制所困扰,而且产品团队在编写规范之前很难评估他们的解决方案,开发人员经常不理解(或不阅读)给出的规范ÿ…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
