线性代数基础概念:向量空间
目录
线性代数基础概念:向量空间
1. 向量空间的定义
2. 向量空间的性质
3. 基底和维数
4. 子空间
5. 向量空间的例子
总结
线性代数基础概念:向量空间
向量空间是线性代数中最基本的概念之一,它为我们提供了一个抽象的框架,用于研究向量和矩阵之间的关系。理解向量空间的概念,是学习线性代数的关键。
1. 向量空间的定义
向量空间是一个集合,其中包含了满足以下条件的向量:
- 加法运算: 任意两个向量相加,结果仍然是该集合中的向量。
- 数乘运算: 任意一个向量乘以一个数,结果仍然是该集合中的向量。
更准确地说,向量空间是一个集合 V,以及定义在 V 上的两种运算:
- 加法运算: V 中任意两个向量 u 和 v 的和 u + v 仍然是 V 中的向量。
- 数乘运算: V 中任意一个向量 u 和任何实数 a 的乘积 au 仍然是 V 中的向量。
例如:
- 二维平面上的所有向量: 我们用 (x, y) 表示二维平面上的一个向量,其中 x 和 y 是实数。两个二维向量相加,或者一个二维向量乘以一个数,结果仍然是二维向量。例如,(1, 2) + (3, 4) = (4, 6), 2 * (1, 2) = (2, 4)。
- 所有实数的集合: 两个实数相加,或者一个实数乘以一个数,结果仍然是实数。例如,2 + 3 = 5, 2 * 3 = 6。
- 所有 n 维向量的集合: n 维向量可以表示为 (x1, x2, ..., xn),其中 x1, x2, ..., xn 是实数。两个 n 维向量相加,或者一个 n 维向量乘以一个数,结果仍然是 n 维向量。例如,(1, 2, 3) + (4, 5, 6) = (5, 7, 9), 2 * (1, 2, 3) = (2, 4, 6)。

2. 向量空间的性质
向量空间具有以下重要性质:
- 加法交换律: u + v = v + u
- 加法结合律: (u + v) + w = u + (v + w)
- 零向量: 存在一个向量 0,使得对于任意向量 u,有 u + 0 = u。
- 负向量: 对于任意向量 u,存在一个向量 -u,使得 u + (-u) = 0。
- 数乘分配律: a(u + v) = au + av
- 数乘结合律: (ab)u = a(bu)
- 单位元: 1u = u
这些性质保证了向量空间中的运算具有良好的性质,使得我们可以进行各种线性代数运算。
3. 基底和维数
基底是向量空间中的一组线性无关的向量,它们可以线性表示向量空间中的所有向量。
线性无关指的是向量空间中的一组向量,其中任何一个向量都不能被其他向量线性表示。
线性组合指的是向量空间中的一组向量,通过数乘和加法运算得到的新的向量。
例如:
- 二维平面上的向量空间: 基底可以是 {(1, 0), (0, 1)},这两个向量线性无关,并且可以线性表示二维平面上的所有向量。例如,向量 (3, 2) 可以表示为 3 * (1, 0) + 2 * (0, 1)。
- 三维空间上的向量空间: 基底可以是 {(1, 0, 0), (0, 1, 0), (0, 0, 1)},这三个向量线性无关,并且可以线性表示三维空间上的所有向量。
维数是向量空间的基底中向量的个数。
例如:
- 二维平面上的向量空间的维数为 2。
- 三维空间上的向量空间的维数为 3。
基底和维数是向量空间的重要特征,它们可以帮助我们理解向量空间的结构。
4. 子空间
子空间是向量空间的一个子集,它本身也是一个向量空间。
例如:
- 二维平面上的所有向量构成一个向量空间,而所有经过原点的直线也构成一个子空间。 这是因为,经过原点的直线上的向量相加,或者乘以一个实数,结果仍然在同一个直线上。
- 三维空间上的所有向量构成一个向量空间,而所有经过原点的平面也构成一个子空间。 这是因为,经过原点的平面上的向量相加,或者乘以一个实数,结果仍然在同一个平面上。
- 所有实数系数的多项式构成的集合是一个向量空间,所有次数不超过 n 的多项式构成的集合是这个向量空间的一个子空间。 这是因为,次数不超过 n 的多项式相加,或者乘以一个实数,结果仍然是次数不超过 n 的多项式。
子空间是向量空间的子集,它继承了向量空间的加法和数乘运算,因此它本身也是一个向量空间。
5. 向量空间的例子
- 实数空间 Rn: 所有 n 维实数向量的集合,构成一个向量空间。
- 复数空间 Cn: 所有 n 维复数向量的集合,构成一个向量空间。
- 多项式空间 Pn: 所有次数不超过 n 的多项式的集合,构成一个向量空间。
- 函数空间: 所有定义在某个区间上的函数的集合,构成一个向量空间。
总结
向量空间是线性代数的基础概念,它为我们提供了研究向量和矩阵的抽象框架。理解向量空间的定义、性质、基底、维数、线性无关、线性组合和子空间等概念,是学习线性代数的关键。

相关文章:

线性代数基础概念:向量空间
目录 线性代数基础概念:向量空间 1. 向量空间的定义 2. 向量空间的性质 3. 基底和维数 4. 子空间 5. 向量空间的例子 总结 线性代数基础概念:向量空间 向量空间是线性代数中最基本的概念之一,它为我们提供了一个抽象的框架,…...

php 抓取淘宝商品评论数据 json
要抓取淘宝商品评论数据,你可以使用PHP的cURL库来发送HTTP请求并获取JSON格式的数据。 API接入流程:需要开放平台或者是封装接口注册账号,并申请相应的API使用权限,以获取必要的密钥和接口文档。获取接口使用权限:接入…...

Java 7新特性深度解析:提升效率与功能
文章目录 Java 7新特性深度解析:提升效率与功能一、Switch中添加对String类型的支持二、数字字面量的改进三、异常处理(捕获多个异常)四、增强泛型推断五、NIO2.0(AIO)新IO的支持六、SR292与InvokeDynamic七、Path接口…...

RHEL9找不到/var/log/dmesg日志文件问题
问题描述 在Rocky Linux 9 服务器上查看启动日志,发现没有/var/log/dmesg文件。 dmesg是什么? dmesg(diagnostic messages)用于打印kernel ring buffer的所有消息。 kernel会将开机信息存储在ring buffer中,如果开机时来不及查看启动信息&…...

是什么让以太坊从众多公链中脱颖而出
以太坊从众多公链中脱颖而出,成为区块链和加密货币领域的一个重要玩家,主要是由于以下几个关键因素: 智能合约: 以太坊是第一个广泛实施智能合约的区块链平台,智能合约允许在区块链上自动执行合同条款,无需…...
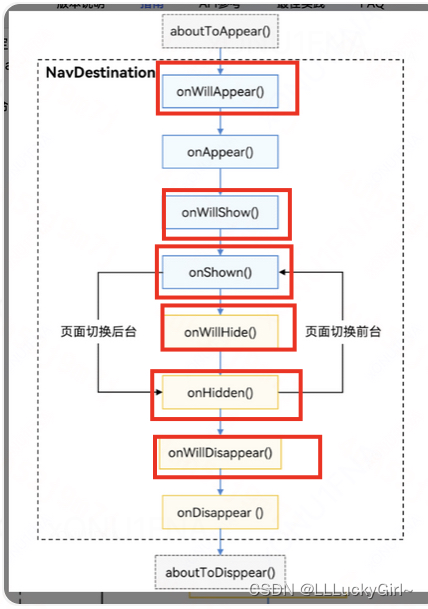
HarmonyOS--路由管理--组件导航 (Navigation)
文档中心 什么是组件导航 (Navigation) ? 1、Navigation是路由容器组件,一般作为首页的根容器,包括单栏(Stack)、分栏(Split)和自适应(Auto)三种显示模式 2、Navigation组件适用于模块内和跨模块的路由切换,一次开发࿰…...

【Linux 命令】文件比较 diff
diff 命令是 Unix 和类 Unix 系统(如 Linux 和 macOS)中用于比较文件内容差异的一个非常有用的命令行工具。它可以逐行比较两个文件的内容,并输出它们之间的差异。这些差异通常以行为单位显示,并且会标记出哪些行是唯一的、添加的…...

猫头虎分享[可灵AI」官方推荐的驯服指南-V1.0
猫头虎分享[可灵AI」官方推荐的驯服指南-V1.0 猫头虎是谁? 大家好,我是 猫头虎,别名猫头虎博主,擅长的技术领域包括云原生、前端、后端、运维和AI。我的博客主要分享技术教程、bug解决思路、开发工具教程、前沿科技资讯、产品评…...

你的硬盘知道的太多:你以为你的秘密真的被删除了吗?
某一天你收到了朋友发给你的一个秘密文件,在看完之后,为了不被别人发现,你决定将文件毁尸灭迹! 你选中文件名称 / 右键 / 删除,好了,文件已经消失了。但你是懂电脑的,知道文件此时还在回收站里面…...
虚拟机的网络配置
📑打牌 : da pai ge的个人主页 🌤️个人专栏 : da pai ge的博客专栏 ☁️ 每一步都向着梦想靠近,坚持就是胜利的序曲 一 …...
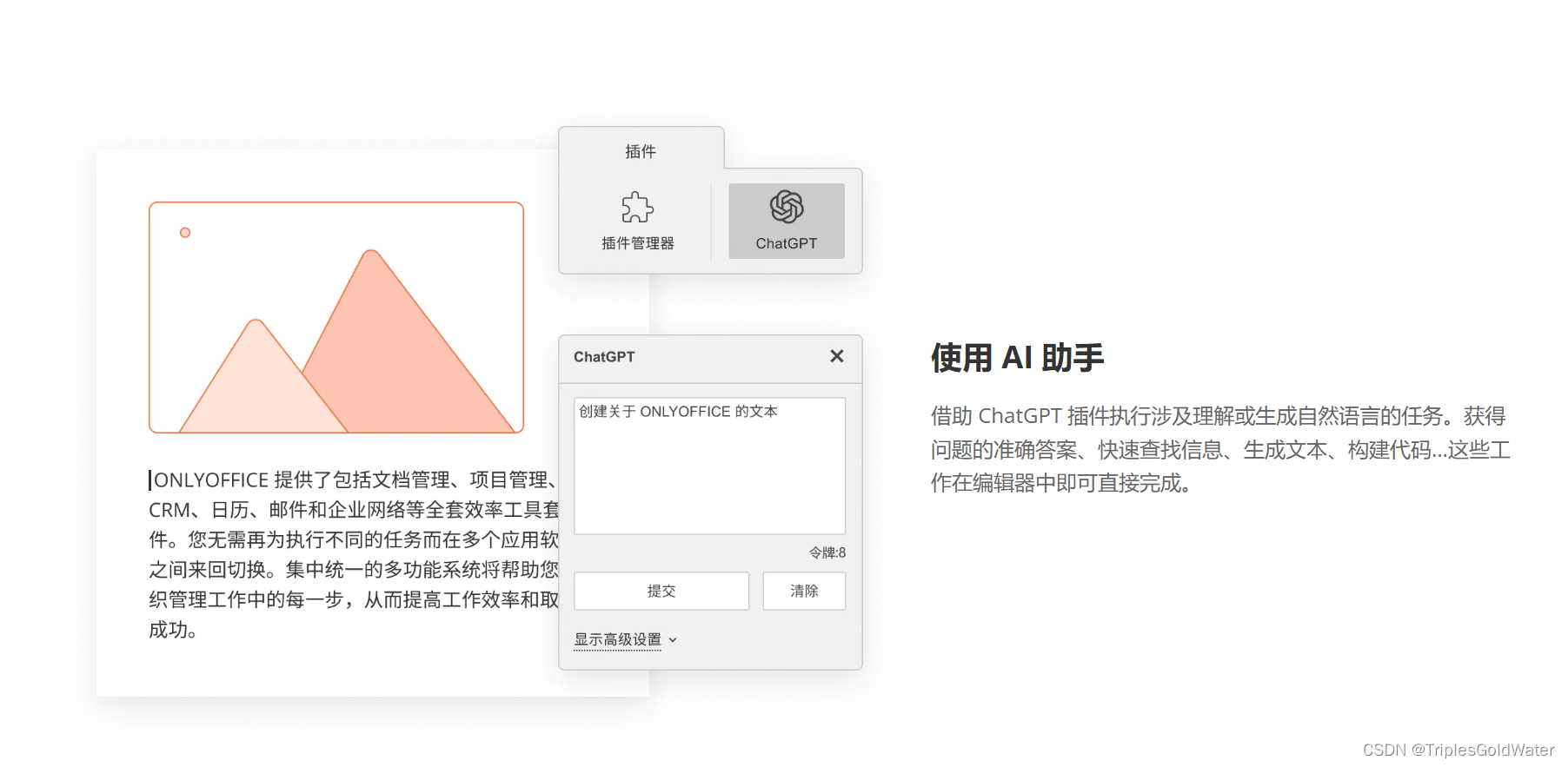
ONLYOFFICE8.1版本桌面编辑器简单测评
ONLYOFFICE官网链接:在线PDF查看器和转换器 | ONLYOFFICE ONLYOFFICE介绍:https://www.onlyoffice.com/zh/office-suite.aspx OnlyOffice 是一款免费且开源的 Office 协作办公套件,支持桌面端和移动端等多平台,由一家领先的 IT 公…...
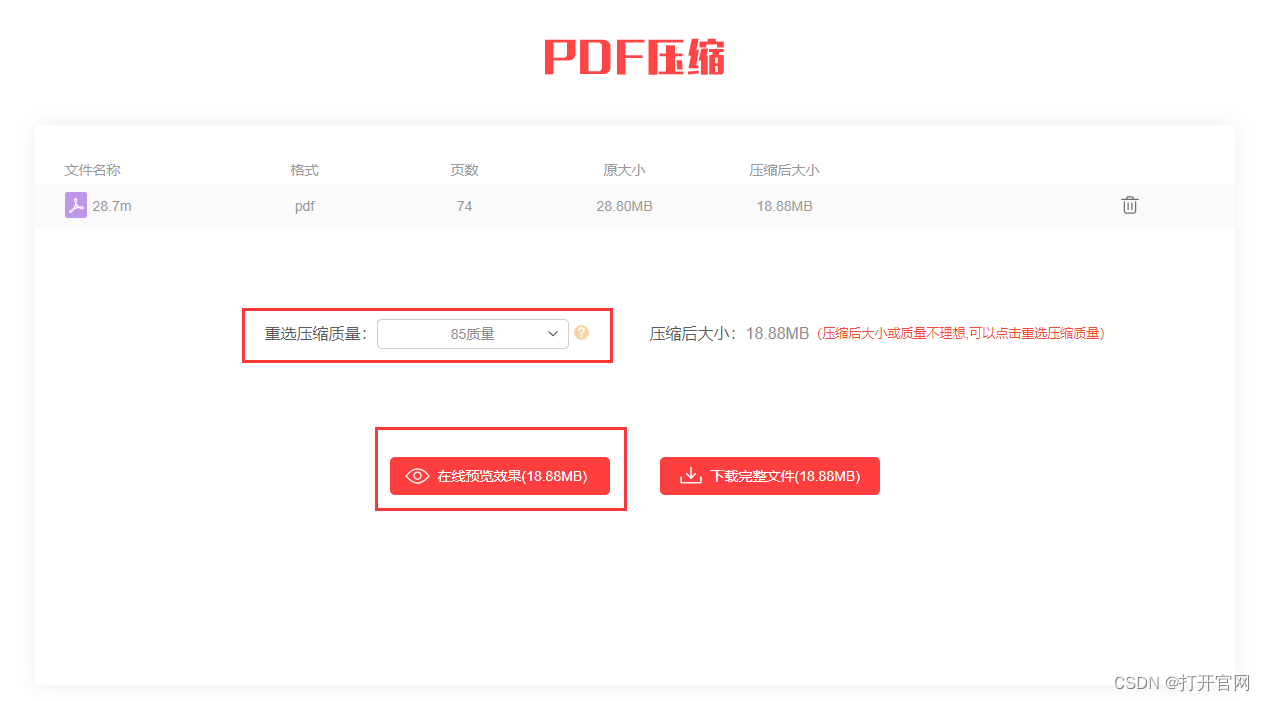
PDF内存如何变小,PDF内存压缩,PDF内存变小怎么调整
在数字化时代,pdf已成为工作、学习和生活中不可或缺的文件格式。它以其跨平台兼容性和安全性受到广大用户的喜爱。然而,随着pdf文件中嵌入的图片、图形和文本内容的增多,文件大小往往会变得相当可观,给文件的传输和存储带来一定的…...

深⼊理解MySQL Innodb存储引擎的缓冲池、事务、索引底层工作原理,掌握 MySQL 主从同步,读写分离技术以及集群的搭建,具备分库分表,SQL调优经验
深入理解MySQL的InnoDB存储引擎是数据库管理员和开发人员的重要技能。以下是对InnoDB存储引擎的缓冲池、事务、索引以及主从同步、读写分离技术和集群搭建的详细原理介绍: ### InnoDB存储引擎 1. **缓冲池(Buffer Pool)**: - 缓冲池是InnoDB存储引擎…...
《HelloGitHub》第 99 期
兴趣是最好的老师,HelloGitHub 让你对编程感兴趣! 简介 HelloGitHub 分享 GitHub 上有趣、入门级的开源项目。 github.com/521xueweihan/HelloGitHub 这里有实战项目、入门教程、黑科技、开源书籍、大厂开源项目等,涵盖多种编程语言 Python、…...

mysql 将一个列按逗号分割为多列
在MySQL中,将一个列按逗号分割为多列通常需要使用字符串函数,如SUBSTRING_INDEX(),配合UNION ALL或CROSS JOIN等操作来实现。 假设有一个表my_table,它有一个列tags,其中存储了逗号分隔的标签值,如下所示&…...

Vue 3中 <script setup> 与生命周期钩子函数的详细解析
Vue 3中 <script setup> 与生命周期钩子函数的详细解析 Vue 3 引入了 <script setup> 语法糖,这是一种简化和集成组件逻辑的新方式。尽管 <script setup> 简化了组件的编写,但仍然可以利用 Vue 提供的生命周期钩子函数来管理组件的生…...

一篇文章入门主成分分析PCA
文章目录 基本概念事件随机变量独立同分布离散型随机变量伯努利分布(两点分布)二项分布几何分布泊松分布 连续型随机变量正态分布 期望方差标准化协方差相关系数线性组合特征值和特征向量特征值分解对称矩阵的特征值分解 齐次线性方程组单位向量基向量矩…...

Android系统为什么lmkd杀到adj 100就代表有低内存?
在Android系统中,lmkd(Low Memory Killer Daemon,低内存终止守护进程)负责监控系统的内存状态,并在内存压力较高时通过终止不必要的进程来释放内存,以维持系统的稳定运行。关于lmkd为何在杀到adj࿰…...
)
d嘤嘤不想求异或喵(牛客周赛49)
题意: 嘤嘤有两个整数 l,r,她想知道区间 [l,r] 所有整数的异或和是多少. 分析: 样例1只有一个数输出1 样例2 1^201^10113 样例3 1^2^301^10^1111^11000 #include<bits/stdc.h> using namespace std; typedef long long ll; ll f(l…...

java反射-动态调用方法
通过字符串动态创建对象,通过字符串动态使用对象方法 package com.hmdp.service.动态调用方法;import java.lang.reflect.Method;public class Main {public static void main(String[] args) throws Exception {String name "javax.swing.JFrame";Clas…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
