Matlab绘制隐函数总结-二维和三维
1.二维隐函数
二维隐函数满足f(x,y)=0f(x,y)=0f(x,y)=0,这里无法得到y=f(x)y=f(x)y=f(x)的形式。不能通过普通函数绘制。
我们要关注的是使用fplot函数和fimplicit函数。
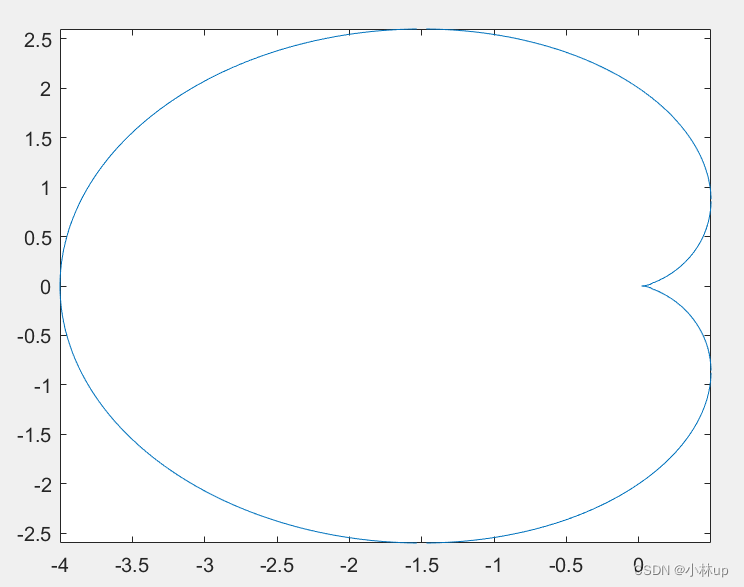
第1种情况:基本隐函数
基本的隐函数形式形如:
x2+y2+2x=2(x2+y2)12x^{2}+y^{2}+2 x=2\left(x^{2}\right.\left.+y^{2}\right)^{\frac{1}{2}}x2+y2+2x=2(x2+y2)21
原来有个ezplot函数的,但是现在Matlab不推荐使用了,可能要慢慢淘汰掉了。老版的写法是
ezplot('x^2+y^2+2*x=2*sqrt(x^2+y^2)')或者
syms x y ezplot(x^2+y^2+2*x-2*sqrt(x^2+y^2))(后面我们也不再谈ezplot函数)
下面是官方推荐的写法:
使用fplot函数
fplot('x^2+y^2+2*x=2*sqrt(x^2+y^2)')
使用fimplicit函数
注意和fplot函数不同,Matlab官方提示:为了获得最佳性能和避免产生警告消息,请使用按元素运算符。例如,使用 x.*y 而不是 x*y。
fimplicit( x.^2+y.^2+2.*x-2.*sqrt(x.^2+y.^2))
或者
fimplicit(@(x,y) x.^2+y.^2+2.*x-2.*sqrt(x.^2+y.^2))
总结:一般的隐函数可以使用fplot函数或者fimplicit函数绘制。
第2种情况:隐函数带变量
形如:
x2+y2+ax=a(x2+y2)12x^{2}+y^{2}+a x=a\left(x^{2}+y^{2}\right)^{\frac{1}{2}}x2+y2+ax=a(x2+y2)21
根据实际需要可将aaa事先具体赋值, 但使用中应注意,绘图语句不能简单采用前面基本格式的 形式 ,不能写作,会报错
a = 2;
fplot('x^2+y^2+a*x-a*sqrt(x^2+y^2)');
因为函数包括单引号时,相当于是符号表达式,变量a的值作为一个参数,不能传进函数,导致fplot()不能正常绘图。
使用fimplicit函数
fplot函数测试了不行,使用fimplicit函数下面的代码是可以的。
a=2;
syms x y
fimplicit(x.^2+y.^2+ a.*x-a.*sqrt(x.^2+y.^2))
总结:带有未知参数的隐函数使用fimplicit函数绘制
第3种情况:带有多个变量的隐函数组的绘图
形如:
f(x,y)=x+y2=a,g(x,y)=x2−y=bf(x, y)=x+y^2=a,\quad g(x, y)=x^2-y=bf(x,y)=x+y2=a,g(x,y)=x2−y=b
不妨令:
a=3,b=−3a=3,b=-3a=3,b=−3
使用fimplicit函数
因为还是带有未知参数的隐函数,我们还是用使用fimplicit函数绘制。
a=3;b=-3;
syms x y
f=x+y^2-a;
g=x^2-y-b;
fimplicit(f);
hold on;
fimplicit(g)
title('x+y^2-a=0 x^2-y-b=0 a=3 b=-3')
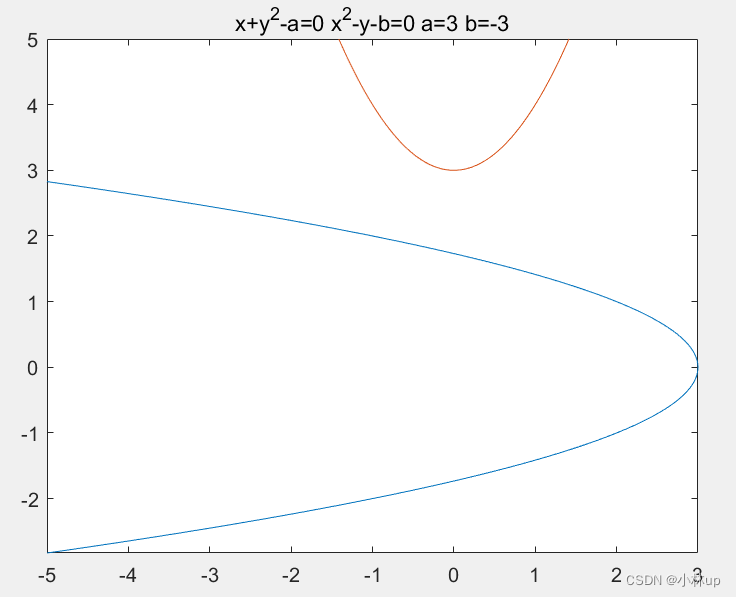
总结:带有多个变量的隐函数组使用fimplicit函数绘制,加上
hold on命令
2.三维隐函数
三维隐函数满足f(x,y,z)=0f(x,y,z)=0f(x,y,z)=0,这里无法得到z=f(x,y)z=f(x,y)z=f(x,y)的形式。不能通过普通函数绘制。
我们要关注的是使用等面值计算函数isosurface和面元渲染函数patch分布实现三维隐函数曲面的绘制方法。
我们使用isosurface的调用方式是
[f,v] = isosurface(X,Y,Z,V,isovalue)
官方的解释是该语句返回由isovalue指定的某个等值面的表面(Faces)和顶点(Vertices)数据,并存放在单独的数组f、v中。我们绘制的是v=f(x,y,z)=0v=f(x,y,z)=0v=f(x,y,z)=0的三维图形,则isovalue=0。
patch函数是面元渲染函数,对曲面进行修饰,相关的调用方式是:patch(X,Y,Z,C)
patch(X,Y,Z,C)
它以三维坐标(X,Y,Z)为顶点,构造三维曲面,c是R G B颜色向量。另一个相关的调用方式是:
patch('Faces',F,'Vertices',V)
它通过包含Faces、Vertices两个的数组F、V来构造三维曲面,F和V可以由等值面函数isosurface计算而得。
对于三元显函数v=f(x,y,z)v=f(x,y,z)v=f(x,y,z) 来说,当v=0v=0v=0时的等值面就是z=g(x,y)z=g(x,y)z=g(x,y)的三维曲面。isosurface函数可以计算v=0v=0v=0的等值面,返回结果包括表面和顶点数据,并存放于数组fff、vvv中,再输入给patch函数,能构造三维曲面,还可以根据需要设置颜色、亮度、三维视角等。画图的步骤可以归纳为:
(1)用meshgrid函数产生网格点,同时可确定坐标范围。
(2)引用隐函数表达式计算格点函数值val。
(3)调用[f,v]=isosurface(x,y,z,val,0)计算隐函数等值面并返回到f、v。
(4)调用patch(‘Faces’,f,‘Vertices’,v,‘facecolor’,‘interp’,‘EdgeColor’,‘k’)对曲面修饰。
[x,y,z]=meshgrid(-1.5:0.1:1.5,-1.5:0.1:1.5,-1.5:0.1:1.5);
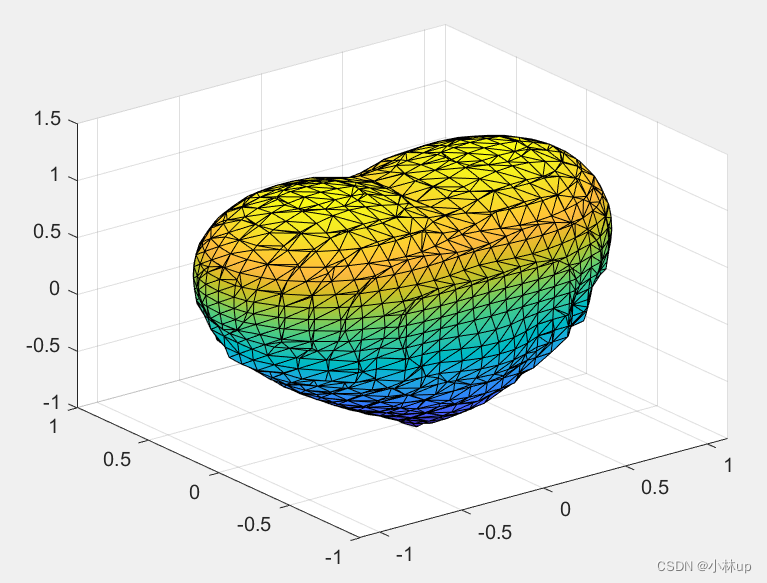
v=(x.^2+(9/4)*y.^2+z.^2-1).^3-x.^2.*z.^3-(9/80)*y.^2.*z.^3;
[f,v]=isosurface(x,y,z,v,0);
p=patch('Faces',f,'Vertices',v,'CData',v(:,3),'facecolor','interp',...'EdgeColor','k');
view(3); grid on;
来看下效果!
相关文章:

Matlab绘制隐函数总结-二维和三维
1.二维隐函数 二维隐函数满足f(x,y)0f(x,y)0f(x,y)0,这里无法得到yf(x)yf(x)yf(x)的形式。不能通过普通函数绘制。 我们要关注的是使用fplot函数和fimplicit函数。 第1种情况:基本隐函数 基本的隐函数形式形如: x2y22x2(x2y2)12x^{2}y^{…...

如何直观地理解傅立叶变换?频域和时域的理解
如何直观地理解傅立叶变换 傅里叶变换连续形式的傅立叶变换如何直观地理解傅立叶变换?一、傅里叶级数1.1傅里叶级数的三角形式1.2 傅里叶级数的复指数形式二、傅里叶变换2.1一维连续傅里叶变换三、频谱和功率谱3.1频谱的获得3.2频谱图的特征3.3频谱图的组成频域(frequency do…...
STC15读取内部ID示例程序
STC15读取内部ID示例程序🎉本案例基于STC15F2K60S2为验证对象。 📑STC15 ID序列介绍 STC15系列STC最新一代STC15系列单片机出厂时都具有全球唯一身份证号码(ID号)。最新STC15系列单片机的程序存储器的最后7个字节单元的值是全球唯一ID号,用…...
Xml格式化与高亮显示
具体请参考:Xml格式化与高亮显示...

【GlobalMapper精品教程】045:空间分析工具(2)——相交
GlobalMapper提供的空间分析(操作)的方法有:交集、并集、单并集、差异、对称差集、相交、重叠、接触、包含、等于、内部、分离等,本文主要讲述相交工具的使用。 文章目录 一、实验数据二、符号化设置三、相交运算四、结果展示五、心灵感悟一、实验数据 加载配套实验数据(…...
4年外包终上岸,我只能说这类公司能不去就不去..
我大学学的是计算机专业,毕业的时候,对于找工作比较迷茫,也不知道当时怎么想的,一头就扎进了一家外包公司,一干就是4年。现在终于跳槽到了互联网公司了,我想说的是,但凡有点机会,千万…...
sklearn降维算法1 - 降维思想与PCA实现
目录1、概述1.1 维度概念2、PCA与SVD2.1 降维实现2.2 重要参数n_components2.2.1 案例:高维数据的可视化2.2.2 最大似然估计自选超参数2.2.3 按信息量占比选超参数1、概述 1.1 维度概念 shape返回的结果,几维几个方括号嵌套 特征矩阵特指二维的 一般来…...

「期末复习」线性代数
第一章 行列式 行列式是一个数,是一个结果三阶行列式的计算:主对角线的乘积全排列与对换逆序数为奇就为奇排列,逆序数为偶就为偶排列对换:定理一:一个排列的任意两个元素对换,排列改变奇偶性(和…...
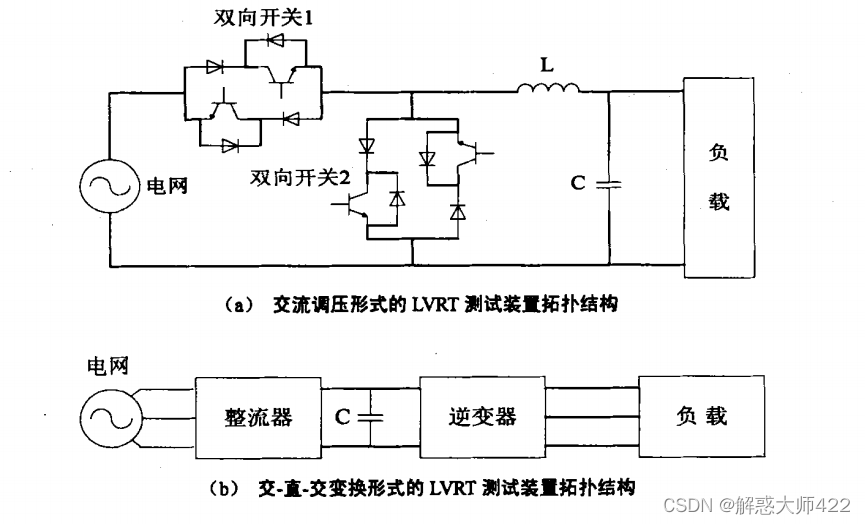
伏并网低电压穿越技术
国内光伏并网低电压穿越要求 略: 低电压穿越方法 当前,光伏电站实现低电压穿越可通过两种方式,即增加硬件设备或者改变控制策略。本节对基于储能设备、基于无功补偿设备、基于无功电流电压支撑控制策略三种实现LVRT的典型方法进行介绍。 …...
opencv的环境搭建
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

C++智能指针
c11的三个智能指针 unique_ptr独占指针,用的最多 shared_ptr记数指针,其次 weak_ptr,shared_ptr的补充,很少用 引用他们要加上头文件#include unique_ptr独占指针: 1.只能有一个智能指针管理内存 2.当指针超出作用域…...
MongoDB--》MongoDB数据库以及可视化工具的安装与使用—保姆级教程
目录 数据库简介 MongoDB数据库的安装 MongoDB数据库的启动 MongoDB数据库环境变量的配置 MongoDB图形化管理工具 数据库简介 在使用MongoDB数据库之前,我们应该要知道我们使用它的原因: 在数据库当中,有常见的三高需求: Hi…...

JAVA 基础题
1. 面向对象有哪些特征?答:继承、封装、多态2. JDK与JRE的区别是什么?答:JDK是java开发时所需环境,它包含了Java开发时需要用到的API,JRE是Java的运行时环境,JDK包含了JRE,他们是包含…...

Flutter desktop端多屏幕展示问题处理
目前越来越多的人用Flutter来做桌面程序的开发,很多应用场景在Flutter开发端还不是很成熟,有些场景目前还没有很好的插件来支持,所以落地Flutter桌面版还是要慎重。 下面来说一下近期我遇到的一个问题,之前遇到一个需要双屏展示的…...

每天10个前端小知识 【Day 9】
👩 个人主页:不爱吃糖的程序媛 🙋♂️ 作者简介:前端领域新星创作者、CSDN内容合伙人,专注于前端各领域技术,成长的路上共同学习共同进步,一起加油呀! ✨系列专栏:前端…...

Elasticsearch的读写搜索过程
问题 Elasticsearch在读写数据的过程是什么样的?你该如何理解这个问题! Elasticsearch的写数据过程 客户端选择一个节点发送请求,这个时候我们所说的这个节点就是协调节点(coordinating node)协调节点对document进行了路由&am…...

线上服务质量的问题该如何去处理?你有什么思路?
线上服务质量的问题该如何去处理?你有什么思路? 目录:导读 发现线上故障 处理线上故障 修复线上故障 运营线上质量 就是前几天有个同学问了我一个问题:目前业内高可用部署主要采用方案? 看到这个问题,…...

IOC 配置,依赖注入的三种方式
xml 配置 顾名思义,就是将bean的信息配置.xml文件里,通过Spring加载文件为我们创建bean。这种方式出现很多早前的SSM项目中,将第三方类库或者一些配置工具类都以这种方式进行配置,主要原因是由于第三方类不支持Spring注解。 优点…...
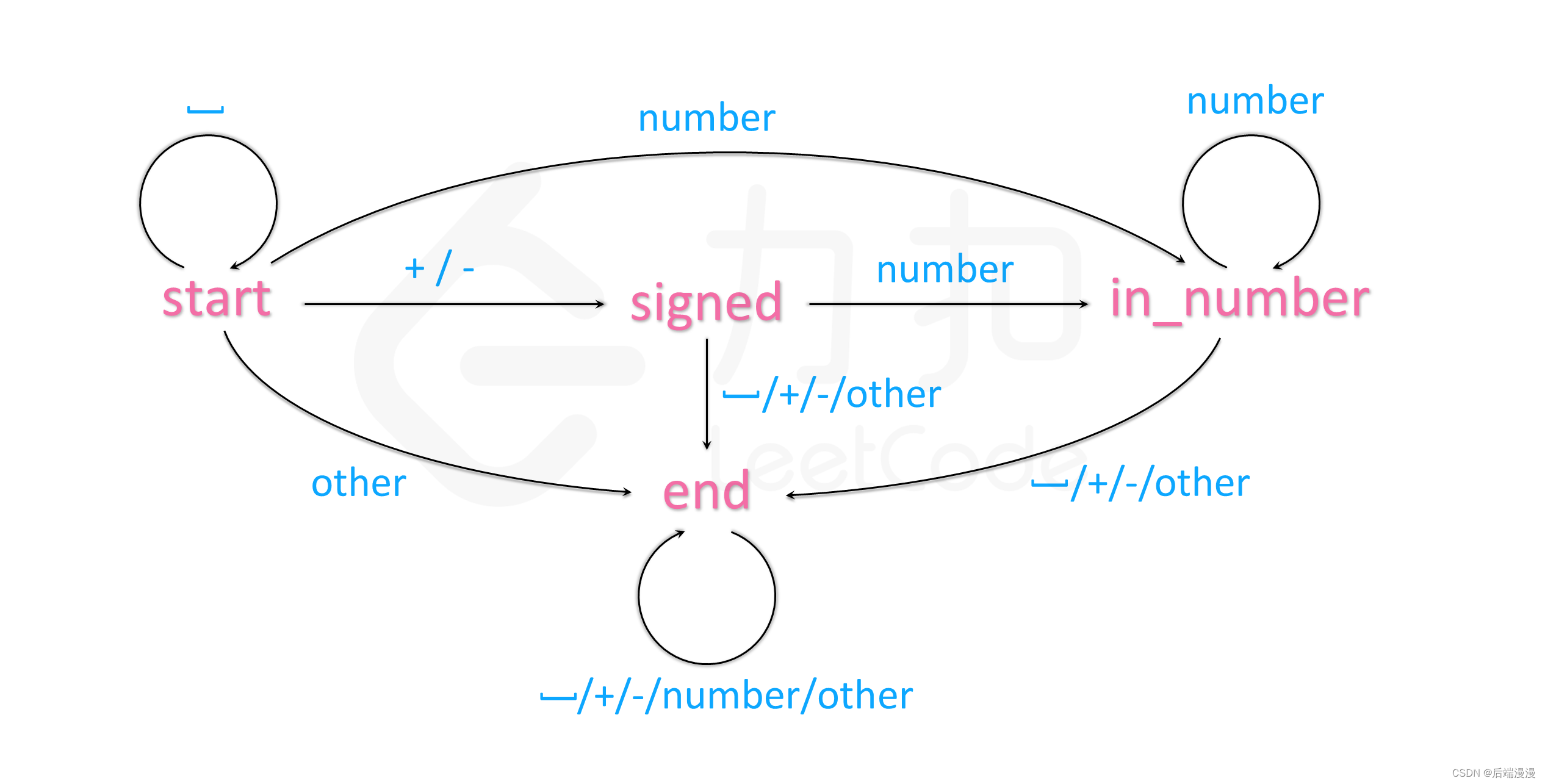
自动机,即有限状态机
文章目录一、问题来源二、题目描述三、题解中的自动机四、自动机学习五、有限状态机的使用场景一、问题来源 今天做力克题目的时候看到了字符串转换整数的一道算法题,其中又看到了题解中有自动机的概念,所以在这里对自动机做个笔记。题目链接 二、题目描…...
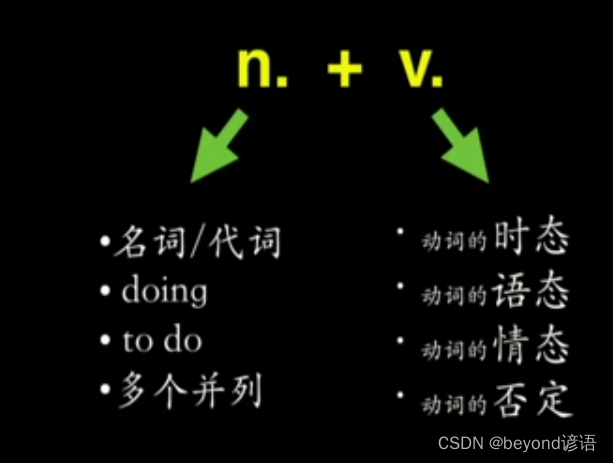
第一部分:简单句——第一章:简单句的核心——二、简单句的核心变化(主语/宾语/表语的变化)
二、简单句的核心变化 简单句的核心变化其实就是 一主一谓(n. v.) 表达一件事情,谓语动词是其中最重要的部分,谓语动词的变化主要有四种:三态加一否(时态、语态、情态、否定),其中…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
