leetcode 403周赛 包含所有1的最小矩形面积||「暴力」
3197. 包含所有 1 的最小矩形面积 II
题目描述:
给你一个二维 二进制 数组 grid。你需要找到 3 个 不重叠、面积 非零 、边在水平方向和竖直方向上的矩形,并且满足 grid 中所有的 1 都在这些矩形的内部。
返回这些矩形面积之和的 最小 可能值。
注意,这些矩形可以相接。
1 < = g r i d . l e n g t h , g r i d [ i ] . l e n g t h < = 30 1 <= grid.length, grid[i].length <= 30 1<=grid.length,grid[i].length<=30
思路:
观察数据范围,n只有30,估计是 O ( n 4 ) O(n^4) O(n4)甚至是 O ( n 5 ) O(n^5) O(n5),所以要想办法暴力
我们只能做到 O ( n 2 ) O(n^2) O(n2)的方法去计算一个区域中用一个矩形覆盖的情况
所以要想办法只枚举两次就能把图形分割成三份,情况如下
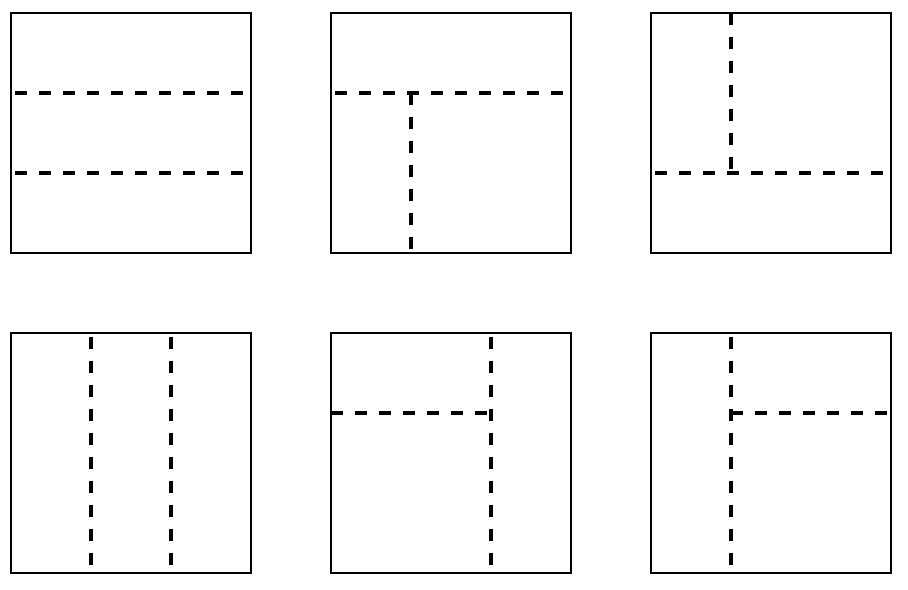
写代码的时候要仔细,注意下标
class Solution {
public:int n, m, tr[35][35];int cal(int x1, int y1, int x2, int y2){bool fuck = 0;int x_max = 0, x_min = 1e9, y_max = 0, y_min = 1e9;for(int i = x1; i <= x2; ++i){for(int j = y1; j <= y2; ++j){if(tr[i][j]){fuck = 1;x_max = max(x_max, i);x_min = min(x_min, i);y_max = max(y_max, j);y_min = min(y_min, j);}}}if(fuck == 0)return 0;return (x_max - x_min + 1) * (y_max - y_min + 1);}int minimumSum(vector<vector<int>>& num) {n = num.size();m = num[0].size();for(int i = 1; i <= n; ++i){for(int j = 1; j <= m; ++j){tr[i][j] = num[i - 1][j - 1];}}int ans = 1e9;for(int i = 1; i <= n; ++i){for(int j = i + 1; j <= n; ++j){ans = min(ans, cal(1,1, i, m) + cal(i + 1, 1, j, m) + cal(j + 1, 1, n, m));}for(int j = 1; j <= m; ++j){ans = min(ans, cal(1, 1, i, j) + cal(i + 1, 1, n, j) + cal(1, j + 1, n, m));ans = min(ans, cal(1, 1, n, j) + cal(1, j + 1, i, m) + cal(i + 1, j + 1, n, m));ans = min(ans, cal(1, 1, i, j) + cal(1, j + 1, i, m) + cal(i + 1, 1, n, m));ans = min(ans, cal(1, 1, i, m) + cal(i + 1, 1, n, j) + cal(i + 1, j + 1, n, m));}}for(int i = 1; i <= m; ++i){for(int j = i + 1; j <= m; ++j){ans = min(ans, cal(1, 1, n, i) + cal(1, i + 1, n, j) + cal(1, j + 1, n, m));}}return ans;}
};
相关文章:

leetcode 403周赛 包含所有1的最小矩形面积||「暴力」
3197. 包含所有 1 的最小矩形面积 II 题目描述: 给你一个二维 二进制 数组 grid。你需要找到 3 个 不重叠、面积 非零 、边在水平方向和竖直方向上的矩形,并且满足 grid 中所有的 1 都在这些矩形的内部。 返回这些矩形面积之和的 最小 可能值。 注意…...

Stable Diffusion web UI 插件
2024.7.3更新,持续更新中 如果需要在linux上自己安装sd,参考:stable diffusion linux安装 插件复制到 /stable-diffusion-webui/extensions 目录下,然后重新启动sd即可 一、插件安装方法 每种插件的安装方法可能略有不同…...

深度学习中的反向传播算法的原理
深度学习中的反向传播算法的原理,以及如何计算梯度 反向传播算法(Backpropagation)是深度学习中最核心的优化技术之一,用于训练神经网络。它基于链式法则,通过从输出层逆向计算误差并逐层传递到输入层来更新模型参数&…...

身处奇瑞看三星:既“开卷“又“起火“,却更难受了
三星"起火" 这几天奇瑞的事情,让大家破防了,纷纷表示国内的就业市场环境普遍恶劣。 那我们转个眼,看看海外企业的情况。 最近一周,三星频频登上新闻,颇有"起火"之势。 在刚步入下半年的 7 月 1 日…...

系统架构设计师教程(清华第2版)<第1章 绪论>解读
系统架构设计师教程 第一章 绪论 1.1 系统架构概述1.1.1 系统架构的定义及发展历程1.1.2 软件架构的常用分类及建模方法1.1.3 软件架构的应用场景1.1.4 软件架构的发展未来1.2 系统架构设计师概述1.2.1 架构设计师的定义、职责和任务1.2.2 架构设计师应具备的专业素质1.3 如何成…...
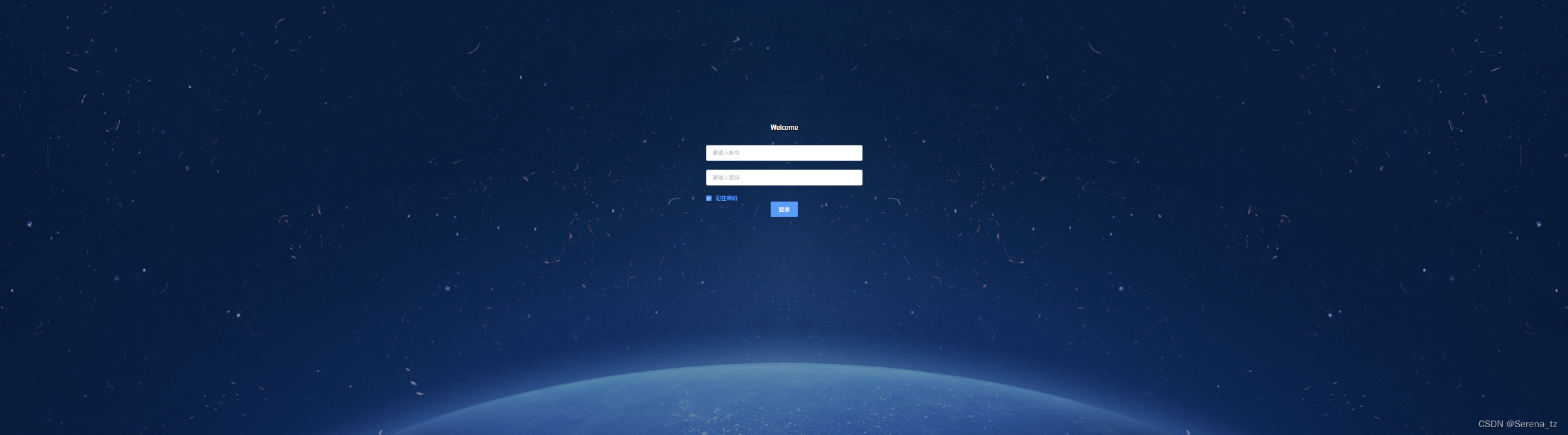
Vue + Element UI + JSEncrypt实现简单登录页面
安装依赖 npm install jsencrypt --save局部引入 import JSEncrypt from jsencrypt/bin/jsencrypt;登录页面index.vue <template><div class"loginbody"><div class"logindata"><div class"logintext"><h2>Wel…...

从“关注流”到“时间线”,搜狐给内容加信任价值
文 | 螳螂观察 作者 | 易不二 在近日第十六季搜狐新闻马拉松活动中,搜狐新闻APP的“时间线”功能备受瞩目。不仅开幕式现场竖了一块“左手时间线,右手关注流”的路牌,张朝阳也着重强调了“时间线”产品的互动方式:“关注是基础&…...
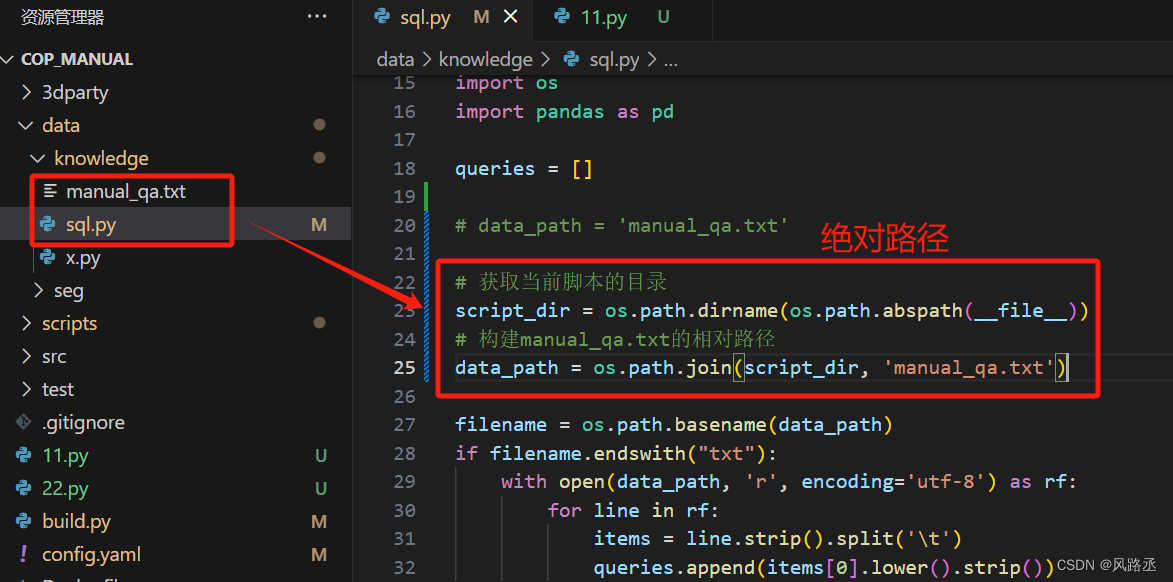
vscode的一些使用问题
vscode使用技巧 1、快捷键(1)打开命令面板(2)注释(3)删除行(4)上下移动光标(5)光标回退(6)复制行(7)插入空白行…...

爬虫-网页基础
HTML 基本语法 HTML:Hyper Text Markup Language, 超文本标记语言,是计算机语言的一种,由元素构成。 p元素 <p>Web 真好玩!</p> 由三大部分组成 开始标签:一对尖括号中间包裹这元素名称元素内容&#x…...

保存huggingface缓存中AI模型(从本地加载AI模型数据)
在github下拉项目后,首次运行时会下拉一堆模型数据,默认是保存在缓存的,如果你的系统盘空间快满的时候就会被系统清理掉,每次运行又重新下拉一次,特别麻烦。 默认下载的缓存路径如下:C:\Users\用户名\.cache\huggingf…...

wps的xlsm和xltm和xlam格式的文件各有什么区别
文章目录 一、前言二、WPS表格文件格式介绍1. .xlsm 文件格式2. .xltm 文件格式3. .xlam 文件格式 三、总结 一、前言 本文将详细介绍WPS表格中三种常见的文件格式:.xlsm、.xltm、和.xlam,并提供通俗易懂的解释和示例,帮助用户理解它们的区别…...

软件性能测试有哪几种测试方法?专业性能测试报告出具
软件性能测试是指对软件系统在特定负载条件下的性能进行评估和验证的过程,目的是确保软件在正常使用的情况下能够满足用户的要求,并在稳定的性能水平下运行,在软件开发过程中起到了至关重要的作用,可以确保软件产品的质量和可靠性…...

JavaScript语言简介与实战应用:从零开始的编程之旅
JavaScript,一种轻量级的、解释型的、面向对象的脚本语言,自1995年由Netscape公司的Brendan Eich设计以来,迅速成为了Web开发中不可或缺的一部分。它不仅能够为静态网页添加动态效果,还能实现客户端与服务器的交互,如今…...

如何理解synchronized锁升级
在Java中,synchronized 关键字是实现线程同步的一种方式,它涉及到锁的升级和释放的过程。理解synchronized 锁的升级可以分为三个阶段:无锁状态、偏向锁状态和轻量级锁状态。 无锁状态: 当对象被创建时,默认处于无锁状…...
for,forEach,for of,map,filter,reduce,every,some)
js【最佳实践】遍历数组的八种方法(含数组遍历 API 的对比)for,forEach,for of,map,filter,reduce,every,some
遍历方法返回值使用场景备注副作用for 循环——遍历数组通用可以改变原数组forEach 循环——遍历数组ES5 新增,不支持中断和异步可以改变原数组for of 循环——遍历数组ES6 新增可以改变原数组map格式化后的数组格式化数组的API不会改变原数组filter过滤后的数组过滤…...

Node.js开发实战 视频教程 下载
ode.js开发实战 视频教程 下载 下载地址 https://download.csdn.net/download/m0_67912929/89487510 01-课程介绍.mp4 02-内容综述.mp4 03-Node.js是什么? .mp4 04-Node.js可以用来做什么?.mp4 05-课程实战项目介绍.mp4 06-什么是技术预研? .mp4 07-Node.js开发环境…...
VS2022(Visual Studio 2022)最新安装教程
1、下载 1、下载地址 - 官网地址:下载 Visual Studio Tools - 免费安装 Windows、Mac、Linux - 根据自己的电脑的 【操作系统】 灵活选择。 2、安装包 【此处为Windows系统安装包】 2、安装 1、打开软件 - 右击【以管理员身份打开】, 2、准备配置 …...

从华为和特斯拉之争,看智能驾驶的未来
“一旦特斯拉完全解决自动驾驶问题并量产Optimus,任何空头都将被消灭,即使是比尔-盖茨也不例外。”7月2日,马斯克再次在社交媒体X上画下了这样的“大饼”。 与此同时,特斯拉的股价在最近的三个交易日也迎来了24%的涨幅,…...

20240705 每日AI必读资讯
📚Retool 刚刚发布了最新2024上半年《人工智能现状报告》 - 收集了约750名技术人员的意见 - 包括开发者、数据团队和各行业的领导者,了解如何利用人工智能产生真正的影响。 🔗 2024上半年《人工智能现状报告》Retool刚刚发布了最新-CSDN b…...

C++ 设计模式之访问者模式
C 设计模式之访问者模式 简介 1、访问者模式 (Visitor)是一种行为型设计模式,它表示一个作用于某对象结构中的各元素的操作。它使你可以在不改变各元素的类的前提下定义作用于这些元素的新操作。 使用该模式可以在不修改已有程序结构的前提…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
