NLP - Softmax与层次Softmax对比
Softmax
Softmax是神经网络中常用的一种激活函数,用于多分类任务。Softmax函数将未归一化的logits转换为概率分布。公式如下:
P ( y i ) = e z i ∑ j = 1 N e z j P(y_i) = \frac{e^{z_i}}{\sum_{j=1}^{N} e^{z_j}} P(yi)=∑j=1Nezjezi
其中, z i z_i zi是类别 i i i的logit, N N N是类别总数。
在大型词汇表情况下,计算Softmax需要对每个词的logit进行指数运算并归一化,这会导致计算成本随词汇表大小线性增长。因此,当词汇表非常大时,计算Softmax的代价非常高。
层次Softmax
层次Softmax(Hierarchical Softmax)是一种通过树结构来加速Softmax计算的方法。它将词汇表组织成一个树结构,每个叶节点代表一个词,每个内部节点代表一个路径选择的二分类器。通过这种方式,可以将计算复杂度从O(N)降低到O(log(N))。
层次Softmax的详细步骤
-
构建层次结构:
- 将词汇表组织成一棵二叉树或霍夫曼树。霍夫曼树可以根据词频来构建,使得高频词的路径更短,从而进一步加速计算。
-
路径表示:
- 对于每个词,通过树从根节点到叶节点的路径来表示。例如,假设词“banana”的路径为[根 -> 右 -> 左]。
-
路径概率计算:
- 每个内部节点都有一个二分类器,计算左子节点或右子节点的概率。
- 目标词的概率是从根节点到该词的路径上所有内部节点概率的乘积。
对于目标词 w w w,其概率表示为:
P ( w ∣ c o n t e x t ) = ∏ n ∈ p a t h ( w ) P ( n ∣ c o n t e x t ) P(w|context) = \prod_{n \in path(w)} P(n|context) P(w∣context)=n∈path(w)∏P(n∣context)
其中, p a t h ( w ) path(w) path(w)表示从根节点到词 w w w的路径上的所有内部节点。
-
训练过程:
- 使用负对数似然损失函数进行优化。
- 对于每个训练样本,计算从根节点到目标词的路径上的所有内部节点的概率,并根据实际路径更新模型参数。
对比分析
| 特点 | Softmax | 层次Softmax |
|---|---|---|
| 计算复杂度 | O(N) | O(log(N)) |
| 适用场景 | 小型词汇表 | 大型词汇表 |
| 实现复杂度 | 简单 | 复杂,需要构建树结构 |
| 计算效率 | 随词汇表大小增加而增加 | 随词汇表大小增加,增长较慢 |
为了更详细地展示层次Softmax与传统Softmax的对比,并包括实际数据和计算过程,下面我们使用一个简化的例子来说明。
案例说明 - 词汇表及其层次结构
假设我们有以下词汇表(词汇频率为假定):
| 词汇 | 频率 |
|---|---|
| apple | 7 |
| banana | 2 |
| cherry | 4 |
| date | 1 |
根据词汇频率,我们构建如下霍夫曼树:
(*)/ \(apple) (*)/ \(cherry) (*)/ \(banana) (date)
计算Softmax概率
假设在某个上下文下,模型输出以下logits:
| 词汇 | Logit z z z |
|---|---|
| apple | 1.5 |
| banana | 0.5 |
| cherry | 1.0 |
| date | 0.2 |
Softmax计算步骤:
- 计算每个词的指数:
e 1.5 = 4.4817 e^{1.5} = 4.4817 e1.5=4.4817
e 0.5 = 1.6487 e^{0.5} = 1.6487 e0.5=1.6487
e 1.0 = 2.7183 e^{1.0} = 2.7183 e1.0=2.7183
e 0.2 = 1.2214 e^{0.2} = 1.2214 e0.2=1.2214
- 计算所有指数的总和:
Z = 4.4817 + 1.6487 + 2.7183 + 1.2214 = 10.0701 Z = 4.4817 + 1.6487 + 2.7183 + 1.2214 = 10.0701 Z=4.4817+1.6487+2.7183+1.2214=10.0701
- 计算每个词的概率:
P ( a p p l e ) = 4.4817 10.0701 ≈ 0.445 P(apple) = \frac{4.4817}{10.0701} \approx 0.445 P(apple)=10.07014.4817≈0.445
P ( b a n a n a ) = 1.6487 10.0701 ≈ 0.164 P(banana) = \frac{1.6487}{10.0701} \approx 0.164 P(banana)=10.07011.6487≈0.164
P ( c h e r r y ) = 2.7183 10.0701 ≈ 0.270 P(cherry) = \frac{2.7183}{10.0701} \approx 0.270 P(cherry)=10.07012.7183≈0.270
P ( d a t e ) = 1.2214 10.0701 ≈ 0.121 P(date) = \frac{1.2214}{10.0701} \approx 0.121 P(date)=10.07011.2214≈0.121
计算层次Softmax概率
我们使用以下假设的特征向量和模型参数来计算每个内部节点的概率:
模型参数:
- 根节点二分类器:
- 权重 w r o o t = [ 0.5 , − 0.2 ] w_{root} = [0.5, -0.2] wroot=[0.5,−0.2]
- 偏置 b r o o t = 0 b_{root} = 0 broot=0
- 右子节点二分类器:
- 权重 w r i g h t = [ 0.3 , 0.4 ] w_{right} = [0.3, 0.4] wright=[0.3,0.4]
- 偏置 b r i g h t = − 0.1 b_{right} = -0.1 bright=−0.1
- 子树根二分类器:
- 权重 w s u b t r e e = [ − 0.4 , 0.2 ] w_{subtree} = [-0.4, 0.2] wsubtree=[−0.4,0.2]
- 偏置 b s u b t r e e = 0.2 b_{subtree} = 0.2 bsubtree=0.2
上下文特征向量:
- x c o n t e x t = [ 1 , 2 ] x_{context} = [1, 2] xcontext=[1,2]
1. 计算根节点概率
z r o o t = w r o o t ⋅ x c o n t e x t + b r o o t z_{root} = w_{root} \cdot x_{context} + b_{root} zroot=wroot⋅xcontext+broot
z r o o t = 0.5 × 1 + ( − 0.2 ) × 2 + 0 z_{root} = 0.5 \times 1 + (-0.2) \times 2 + 0 zroot=0.5×1+(−0.2)×2+0
z r o o t = 0.5 − 0.4 z_{root} = 0.5 - 0.4 zroot=0.5−0.4
z r o o t = 0.1 z_{root} = 0.1 zroot=0.1
使用sigmoid函数计算概率:
P ( l e f t ∣ c o n t e x t ) r o o t = σ ( z r o o t ) P(left|context)_{root} = \sigma(z_{root}) P(left∣context)root=σ(zroot)
P ( l e f t ∣ c o n t e x t ) r o o t = 1 1 + e − 0.1 P(left|context)_{root} = \frac{1}{1 + e^{-0.1}} P(left∣context)root=1+e−0.11
P ( l e f t ∣ c o n t e x t ) r o o t ≈ 1 1 + 0.9048 P(left|context)_{root} \approx \frac{1}{1 + 0.9048} P(left∣context)root≈1+0.90481
P ( l e f t ∣ c o n t e x t ) r o o t ≈ 0.525 P(left|context)_{root} \approx 0.525 P(left∣context)root≈0.525
P ( r i g h t ∣ c o n t e x t ) r o o t = 1 − P ( l e f t ∣ c o n t e x t ) r o o t P(right|context)_{root} = 1 - P(left|context)_{root} P(right∣context)root=1−P(left∣context)root
P ( r i g h t ∣ c o n t e x t ) r o o t = 1 − 0.525 P(right|context)_{root} = 1 - 0.525 P(right∣context)root=1−0.525
P ( r i g h t ∣ c o n t e x t ) r o o t ≈ 0.475 P(right|context)_{root} \approx 0.475 P(right∣context)root≈0.475
2. 计算右子节点概率
z r i g h t = w r i g h t ⋅ x c o n t e x t + b r i g h t z_{right} = w_{right} \cdot x_{context} + b_{right} zright=wright⋅xcontext+bright
z r i g h t = 0.3 × 1 + 0.4 × 2 − 0.1 z_{right} = 0.3 \times 1 + 0.4 \times 2 - 0.1 zright=0.3×1+0.4×2−0.1
z r i g h t = 0.3 + 0.8 − 0.1 z_{right} = 0.3 + 0.8 - 0.1 zright=0.3+0.8−0.1
z r i g h t = 1.0 z_{right} = 1.0 zright=1.0
使用sigmoid函数计算概率:
P ( l e f t ∣ c o n t e x t ) r i g h t = σ ( z r i g h t ) P(left|context)_{right} = \sigma(z_{right}) P(left∣context)right=σ(zright)
P ( l e f t ∣ c o n t e x t ) r i g h t = 1 1 + e − 1.0 P(left|context)_{right} = \frac{1}{1 + e^{-1.0}} P(left∣context)right=1+e−1.01
P ( l e f t ∣ c o n t e x t ) r i g h t ≈ 1 1 + 0.3679 P(left|context)_{right} \approx \frac{1}{1 + 0.3679} P(left∣context)right≈1+0.36791
P ( l e f t ∣ c o n t e x t ) r i g h t ≈ 0.731 P(left|context)_{right} \approx 0.731 P(left∣context)right≈0.731
P ( r i g h t ∣ c o n t e x t ) r i g h t = 1 − P ( l e f t ∣ c o n t e x t ) r i g h t P(right|context)_{right} = 1 - P(left|context)_{right} P(right∣context)right=1−P(left∣context)right
P ( r i g h t ∣ c o n t e x t ) r i g h t = 1 − 0.731 P(right|context)_{right} = 1 - 0.731 P(right∣context)right=1−0.731
P ( r i g h t ∣ c o n t e x t ) r i g h t ≈ 0.269 P(right|context)_{right} \approx 0.269 P(right∣context)right≈0.269
3. 计算子树根节点概率
z s u b t r e e = w s u b t r e e ⋅ x c o n t e x t + b s u b t r e e z_{subtree} = w_{subtree} \cdot x_{context} + b_{subtree} zsubtree=wsubtree⋅xcontext+bsubtree
z s u b t r e e = − 0.4 × 1 + 0.2 × 2 + 0.2 z_{subtree} = -0.4 \times 1 + 0.2 \times 2 + 0.2 zsubtree=−0.4×1+0.2×2+0.2
z s u b t r e e = − 0.4 + 0.4 + 0.2 z_{subtree} = -0.4 + 0.4 + 0.2 zsubtree=−0.4+0.4+0.2
z s u b t r e e = 0.2 z_{subtree} = 0.2 zsubtree=0.2
使用sigmoid函数计算概率:
P ( l e f t ∣ c o n t e x t ) s u b t r e e = σ ( z s u b t r e e ) P(left|context)_{subtree} = \sigma(z_{subtree}) P(left∣context)subtree=σ(zsubtree)
P ( l e f t ∣ c o n t e x t ) s u b t r e e = 1 1 + e − 0.2 P(left|context)_{subtree} = \frac{1}{1 + e^{-0.2}} P(left∣context)subtree=1+e−0.21
P ( l e f t ∣ c o n t e x t ) s u b t r e e ≈ 1 1 + 0.8187 P(left|context)_{subtree} \approx \frac{1}{1 + 0.8187} P(left∣context)subtree≈1+0.81871
P ( l e f t ∣ c o n t e x t ) s u b t r e e ≈ 0.55 P(left|context)_{subtree} \approx 0.55 P(left∣context)subtree≈0.55
P ( r i g h t ∣ c o n t e x t ) s u b t r e e = 1 − P ( l e f t ∣ c o n t e x t ) s u b t r e e P(right|context)_{subtree} = 1 - P(left|context)_{subtree} P(right∣context)subtree=1−P(left∣context)subtree
P ( r i g h t ∣ c o n t e x t ) s u b t r e e = 1 − 0.55 P(right|context)_{subtree} = 1 - 0.55 P(right∣context)subtree=1−0.55
P ( r i g h t ∣ c o n t e x t ) s u b t r e e ≈ 0.45 P(right|context)_{subtree} \approx 0.45 P(right∣context)subtree≈0.45
计算各个词的层次Softmax概率
1. apple
路径为[根 -> 左]
P ( a p p l e ) = P ( l e f t ∣ c o n t e x t ) r o o t ≈ 0.525 P(apple) = P(left|context)_{root} \approx 0.525 P(apple)=P(left∣context)root≈0.525
2. banana
路径为[根 -> 右 -> 右 -> 左]
P ( b a n a n a ) = P ( r i g h t ∣ c o n t e x t ) r o o t × P ( r i g h t ∣ c o n t e x t ) r i g h t × P ( l e f t ∣ c o n t e x t ) s u b t r e e P(banana) = P(right|context)_{root} \times P(right|context)_{right} \times P(left|context)_{subtree} P(banana)=P(right∣context)root×P(right∣context)right×P(left∣context)subtree
P ( b a n a n a ) ≈ 0.475 × 0.269 × 0.55 P(banana) \approx 0.475 \times 0.269 \times 0.55 P(banana)≈0.475×0.269×0.55
P ( b a n a n a ) ≈ 0.0702 P(banana) \approx 0.0702 P(banana)≈0.0702
3. cherry
路径为[根 -> 右 -> 左]
P ( c h e r r y ) = P ( r i g h t ∣ c o n t e x t ) r o o t × P ( l e f t ∣ c o n t e x t ) r i g h t P(cherry) = P(right|context)_{root} \times P(left|context)_{right} P(cherry)=P(right∣context)root×P(left∣context)right
P ( c h e r r y ) ≈ 0.475 × 0.731 P(cherry) \approx 0.475 \times 0.731 P(cherry)≈0.475×0.731
P ( c h e r r y ) ≈ 0.3472 P(cherry) \approx 0.3472 P(cherry)≈0.3472
4. date
路径为[根 -> 右 -> 右 -> 右]
P ( d a t e ) = P ( r i g h t ∣ c o n t e x t ) r o o t × P ( r i g h t ∣ c o n t e x t ) r i g h t × P ( r i g h t ∣ c o n t e x t ) s u b t r e e P(date) = P(right|context)_{root} \times P(right|context)_{right} \times P(right|context)_{subtree} P(date)=P(right∣context)root×P(right∣context)right×P(right∣context)subtree
P ( d a t e ) ≈ 0.475 × 0.269 × 0.45 P(date) \approx 0.475 \times 0.269 \times 0.45 P(date)≈0.475×0.269×0.45
P ( d a t e ) ≈ 0.0575 P(date) \approx 0.0575 P(date)≈0.0575
概率总结
| 词汇 | Softmax 概率 | 层次Softmax 概率 |
|---|---|---|
| apple | 0.445 | 0.525 |
| banana | 0.164 | 0.0702 |
| cherry | 0.270 | 0.3472 |
| date | 0.121 | 0.0575 |
以上结果显示了传统Softmax和层次Softmax的概率计算方法及其结果。通过构建霍夫曼树,层次Softmax显著减少了计算复杂度,特别适用于处理大规模词汇表的任务。
Softmax与层次Softmax总结
| 特点 | Softmax | 层次Softmax |
|---|---|---|
| 计算复杂度 | O(N) | O(log(N)) |
| 优点 | 简单直接,适用于小型词汇表 | 计算效率高,适用于大规模词汇表 |
| 缺点 | 计算量大,随着词汇表大小增加而线性增加 | 需要构建和维护层次结构,模型复杂性增加 |
| 适用场景 | 词汇表较小的多分类问题 | 词汇表非常大的自然语言处理任务,如语言建模和机器翻译 |
总结来说,层次Softmax通过树结构优化了大词汇表的概率计算,使其在处理大型词汇表的任务中具有显著优势,而传统Softmax则更适合小型词汇表的场景。
相关文章:

NLP - Softmax与层次Softmax对比
Softmax Softmax是神经网络中常用的一种激活函数,用于多分类任务。Softmax函数将未归一化的logits转换为概率分布。公式如下: P ( y i ) e z i ∑ j 1 N e z j P(y_i) \frac{e^{z_i}}{\sum_{j1}^{N} e^{z_j}} P(yi)∑j1Nezjezi 其中&#…...
HttpServer内存马
HttpServer内存马 基础知识 一些基础的方法和类 HttpServer:HttpServer主要是通过带参的create方法来创建,第一个参数InetSocketAddress表示绑定的ip地址和端口号。第二个参数为int类型,表示允许排队的最大TCP连接数,如果该值小…...
51单片机-让一个LED灯闪烁、流水灯(涉及:自定义单片机的延迟时间)
目录 设置单片机的延迟(睡眠)函数查看单片机的时钟频率设置系统频率、定时长度、指令集 完整代码生成HEX文件下载HEX文件到单片机流水灯代码 (自定义延迟时间) 设置单片机的延迟(睡眠)函数 查看单片机的时钟频率 检测前单片机必…...

MYSQL原理、设计与应用
概述 数据库(Database,DB)是按照数据结构来组织、存储和管理数据的仓库,其本身可被看作电子化的文件柜,用户可以对文件中的数据进行增删改查等操作。 数据库系统是指在计算机系统中引入数据库后的系统,除了数据库,还…...

flask项目部署总结
这个部署的时候要用虚拟环境,cd进项目文件夹 python3 -m venv myenv source myenv/bin/activate激活 之后就安装一些库包之类的,(flask,requests,bs4,等等) 最重要的是要写.flaskenv文件并且pip install 一个能运行…...

【总线】AXI4第八课时:介绍AXI的 “原子访问“ :独占访问(Exclusive Access)和锁定访问(Locked Access)
大家好,欢迎来到今天的总线学习时间!如果你对电子设计、特别是FPGA和SoC设计感兴趣,那你绝对不能错过我们今天的主角——AXI4总线。作为ARM公司AMBA总线家族中的佼佼者,AXI4以其高性能和高度可扩展性,成为了现代电子系统中不可或缺的通信桥梁…...

Java面试八股之MYISAM和INNODB有哪些不同
MYISAM和INNODB有哪些不同 MyISAM和InnoDB是MySQL数据库中两种不同的存储引擎,它们在设计哲学、功能特性和性能表现上存在显著差异。以下是一些关键的不同点: 事务支持: MyISAM 不支持事务,没有回滚或崩溃恢复的能力。 InnoDB…...
)
大数据面试题之数据库(2)
数据库中存储引擎MvlSAM与InnoDB的区别 Mylsam适用于什么场景? InnoDB和Mvlsam针对读写场景? MySQL Innodb实现了哪个隔离级别? InnoDB数据引擎的特点 InnoDB用什么索引 Hash索引缺点 数据库索引的类型,各有什么优缺点? MySQL的索引有哪些?索引…...

1421-04SF 同轴连接器
型号简介 1421-04SF是Southwest Microwave的2.4 mm 同轴连接器。这款连接器外壳和耦合螺母: 不锈钢 CRES 合金 UNS-S30300, 按照 ASTM A582 标准制造,并按照 ASTM A967-99 标准进行钝化处理。金镀层可以提供更低的接触电阻和更好的耐腐蚀性。 型号特点 50 欧姆密封…...

第一节-k8s架构图
一个Deployment,可以由多个不同Node下的Pod组成,每个Pod又由多个Container组成。 区分Deployment是用Labels(key:value),区分Pod是用PodName,区分Container是用ContainerName。 一个Node可以包含多个不同Deployment中的pod&…...
【Proteus】按键的实现『⒉种』
🚩 WRITE IN FRONT 🚩 🔎 介绍:"謓泽"正在路上朝着"攻城狮"方向"前进四" 🔎🏅 荣誉:2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4、2021|2222年获评…...

Windows 11 安装 Python 3.11 完整教程
Windows 11 安装 Python 3.11 完整教程 一、安装包安装 1. 下载 Python 3.11 安装包 打开浏览器,访问 Python 官方下载页面。点击“Download Python 3.11”,下载适用于 Windows 的安装包(Windows installer)。 2. 安装 Python 3.11 运行下载的安装包 python-3.11.x-amd6…...

外呼系统的功能有哪些
1. 自动拨号 - 系统能够自动拨打电话,避免了手动拨号的繁琐过程。 - 可以根据设定的电话号码列表自动拨号,提高电话接触率和工作效率。 2. 呼叫分配 - 根据事先设定的规则和策略,将呼叫分配给不同的坐席或代表。 - 确保呼叫平均分配和资源优…...
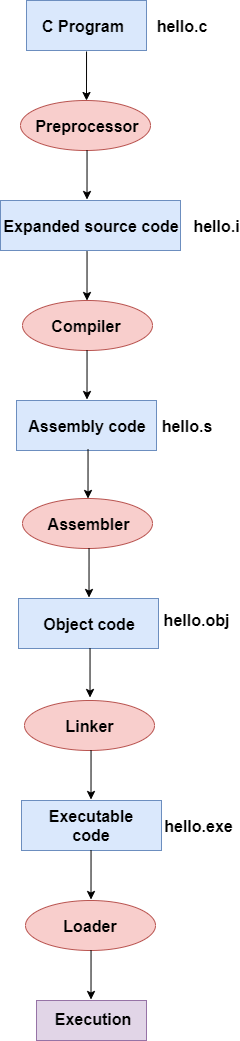
【C语言】C语言 4 个编译过程详解
C语言的编译过程涉及几个关键步骤、概念和细节,每个步骤都有助于将人类可读的源代码转换为可执行的机器码。以下是详细的解释和示例: 一、什么是编译? 编译是将源代码转换为目标代码的过程。它是在编译器的帮助下完成的。编译器检查源代码是…...

Linux 常见的几种编辑器的操作步骤
在大多数命令行文本编辑器中,保存并关闭文件的操作方式基本相似。以下是常见的几种编辑器的操作步骤: 使用 vi 编辑器保存并关闭文件 编辑文件: sudo vi /path/to/file 编辑内容: 按 i 进入插入模式,编辑文件内容。 …...
LabVIEW汽车转向器测试系统
绍了一种基于LabVIEW的汽车转向器测试系统。该系统集成了数据采集、控制和分析功能,能够对转向器进行高效、准确的测试。通过LabVIEW平台,实现了对转向器性能参数的实时监测和分析,提升了测试效率和数据精度,为汽车转向器的研发和…...

image媒体组件属性配合swiper轮播
图片组件(image) 先插入个图片试试,插入图片用src属性,这是图片: 代码如下: <template><view><swiper indicator-dots indicator-color "#126bae" indicator-active-color &…...
nginx的匹配及重定向
一、nginx的匹配: nginx中location的优先级和匹配方式: 1.精确匹配:location / 对字符串进行完全匹配,必须完全符合 2.正则匹配:location ^~ ^~ 前缀匹配,以什么为开头 ~区分大小写的匹配 ~* 不区分…...

云计算【第一阶段(23)】Linux系统安全及应用
一、账号安全控制 1.1、账号安全基本措施 1.1.1、系统账号清理 将非登录用户的shell设为/sbin/nologin锁定长期不使用的账号删除无用的账号 1.1.1.1、实验1 用于匹配以/sbin/nologin结尾的字符串,$ 表示行的末尾。 (一般是程序用户改为nologin&…...

YUM——简介、安装(Ubuntu22.04)
1、简介 YUM(Yellowdog Updater, Modified)是一个开源的命令行软件包管理工具,主要用于基于 RPM 包管理系统的 Linux 发行版,如 CentOS、Red Hat Enterprise Linux (RHEL) 和 Fedora。YUM 使用户能够轻松地安装、更新、删除和管理…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
