【pytorch12】什么是梯度
说明
- 导数
- 偏微分
- 梯度
梯度:是一个向量,向量的每一个轴是每一个方向上的偏微分
梯度是有方向也有大小,梯度的方向代表函数在当前点的一个增长的方向,然后这个向量的长度代表了这个点增长的速率

蓝色代表比较小的值,红色代表比较大的值,中间的箭头比较长,方向是由一个极小值指向一个极大值,因此中间这部分梯度反应了函数的增长的方向,说明了从这个方向增长这个方向是最快的
如何搜索到一个极小值?
一般情况下我们搜索的是极小值,如果想要搜索极大值的话,可以把loss变成负号,就可以通过搜索一个极小值解来搜索极大值解

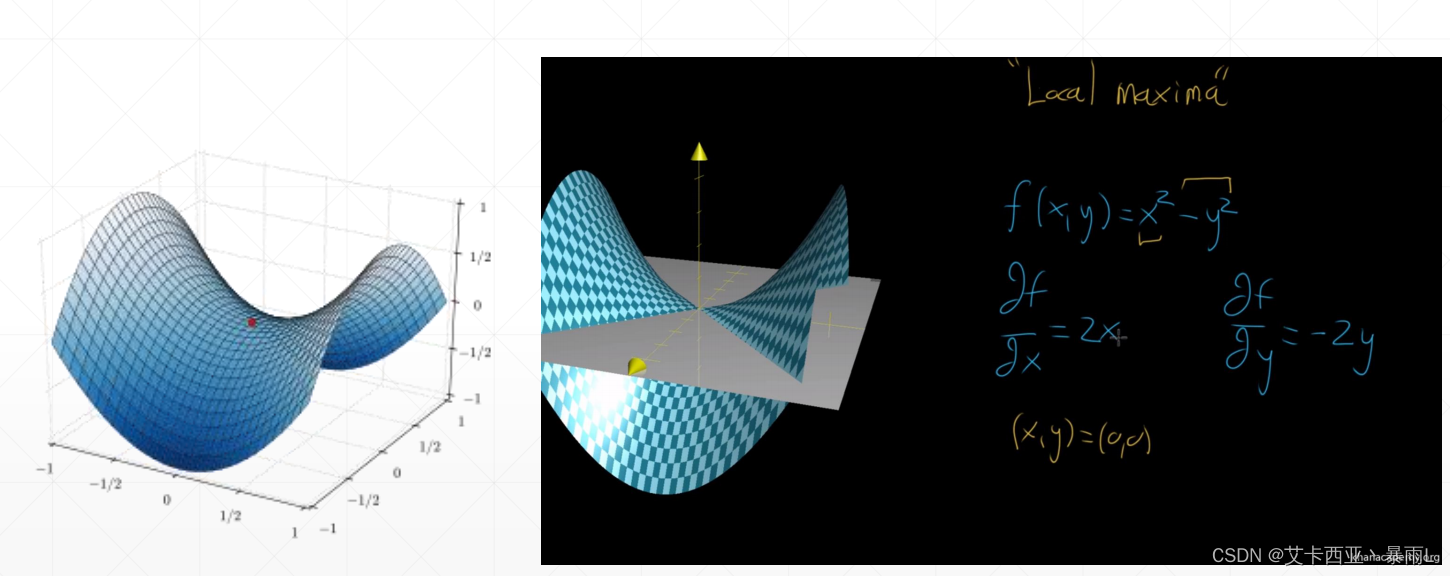
所以这个函数的梯度是(2 θ 1 \theta_{1} θ1,2 θ 2 \theta_{2} θ2),再求(0,0)处的一个梯度情况,因此有时候会陷入到一个局部最小值的情况
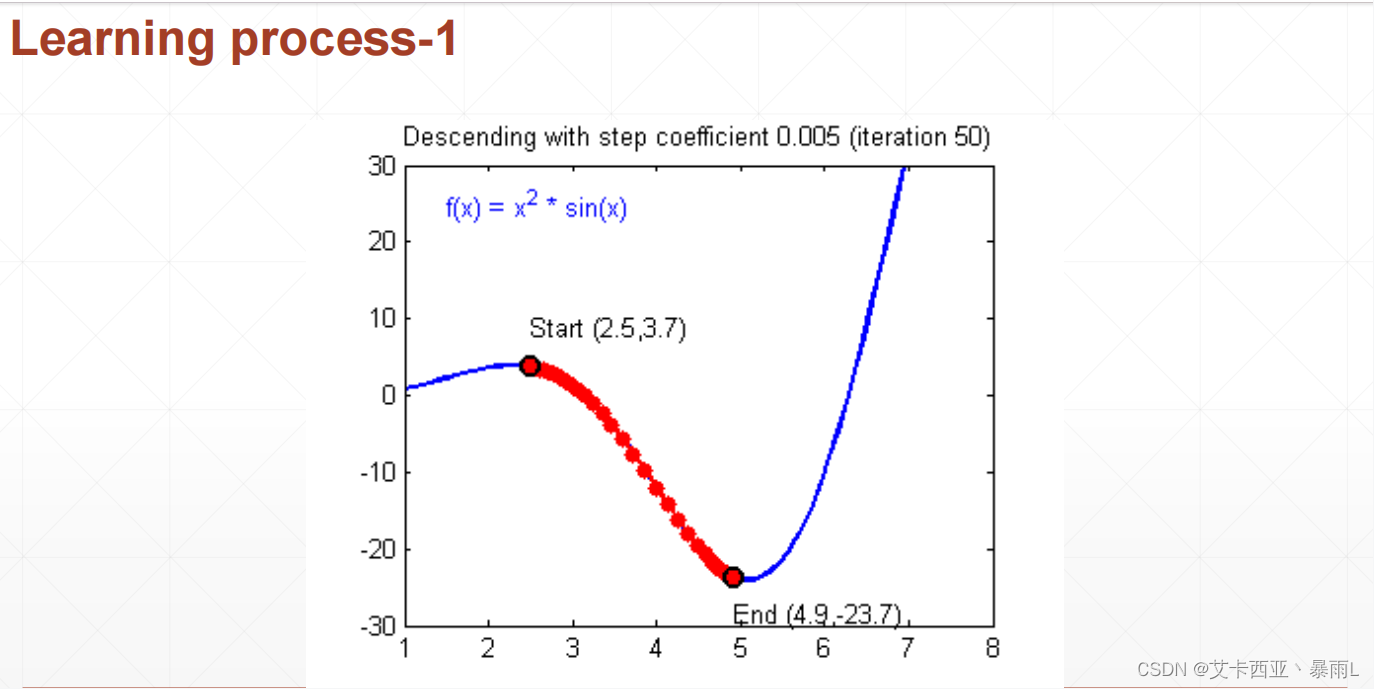
红色是最原始版本的梯度下降来搜索会卡在马鞍的点上

对于任何的一个点和另外的一个点,我们拉一条直线,这条直线中间的中点以及中点所对应的函数的值,例如定义为z1,z2且z1>z2,叫做凸函数,对于这种情况可以找到一个全局最优解
存在且不太常见的
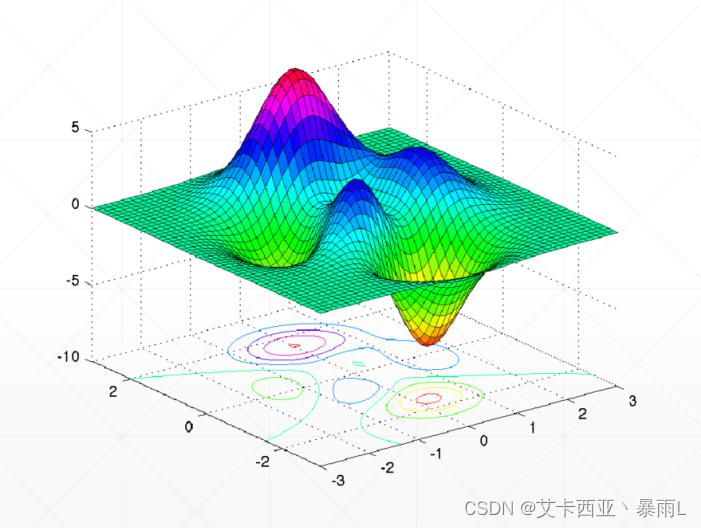
存在局部极大和局部极小,存在多个局部极小值
实际的例子:ResNet-56的平面

对于函数的输出可能有无数多个w参数,对于ResNet可以有上千万个W的参数f=(w1,w2,…),把上千万的自变量可视化到一个二维的平面,可能会陷入到无数多的局部极小值中,即使有全局最小值解,因此对于一个深层次的神经网络,取搜索的时候可能找到一个表现不满意的因为此时的解可能是一个局部极小值解,因此网络的精度不会特别高,Resnet加了一个shortcut的模块,在神经网络的旁边加了一条支路,发现神经网络可以变得很深同时也可以优化的很好,可视化后会变成第二个平面
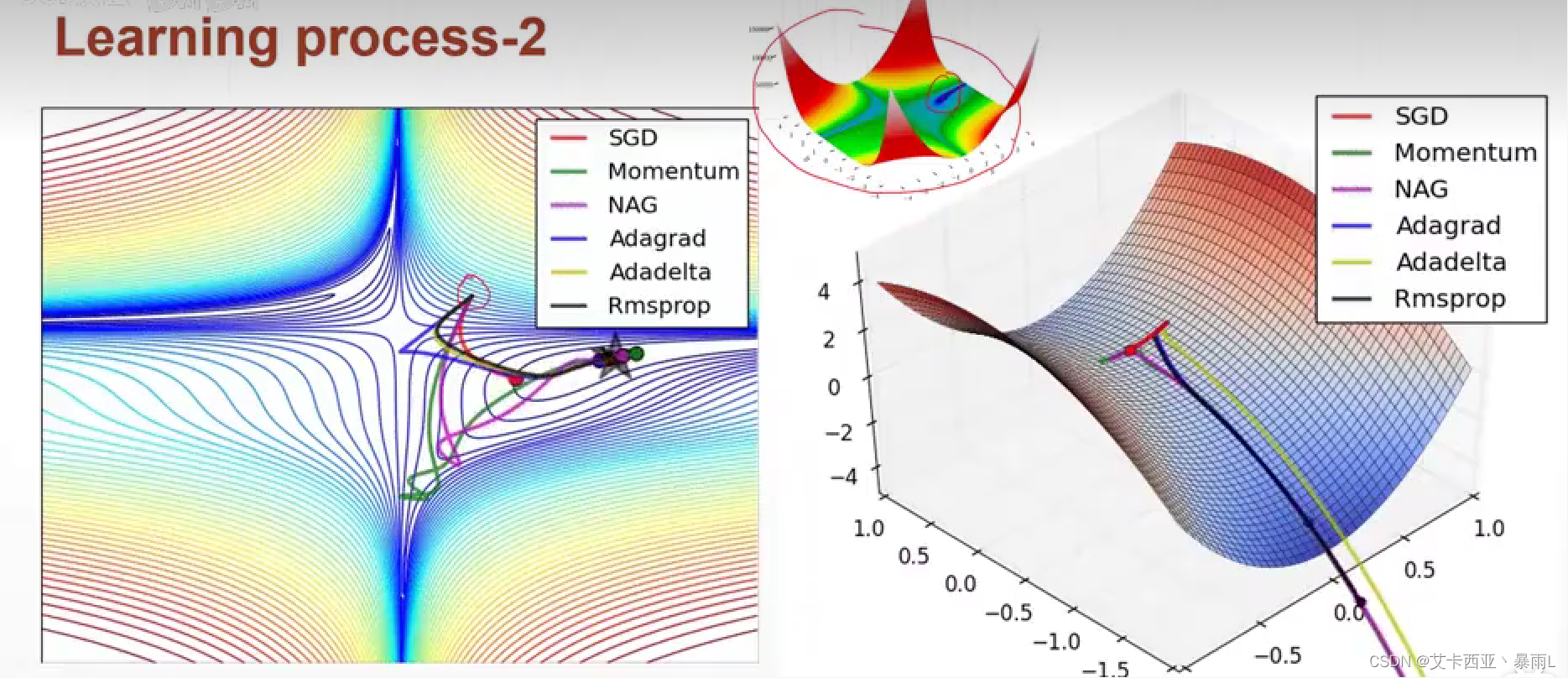
使用梯度来搜索最小值的情况下,除了会遇到局部最小值,还可能遇到鞍点
优化器表现
- 初始状态
- 学习率
- 动量(即如何逃离局部极小值)
初始状态
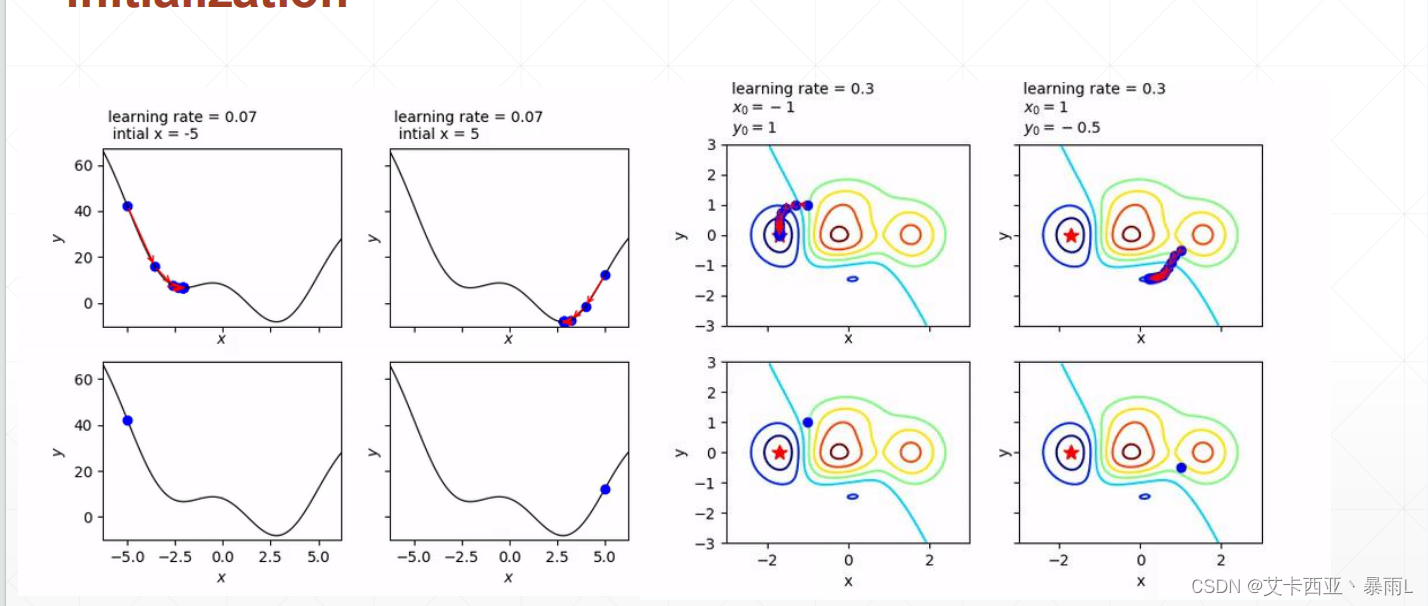
对于初始状态的不同,会影响找到的是全局解还是局部极小值这样的情况,搜索的路径也可能不一样,因此大家再做深度学习的时候函数的全职一定要初始化,而且初始化的时候如果没有把握就按照目前主流的初始化的方法
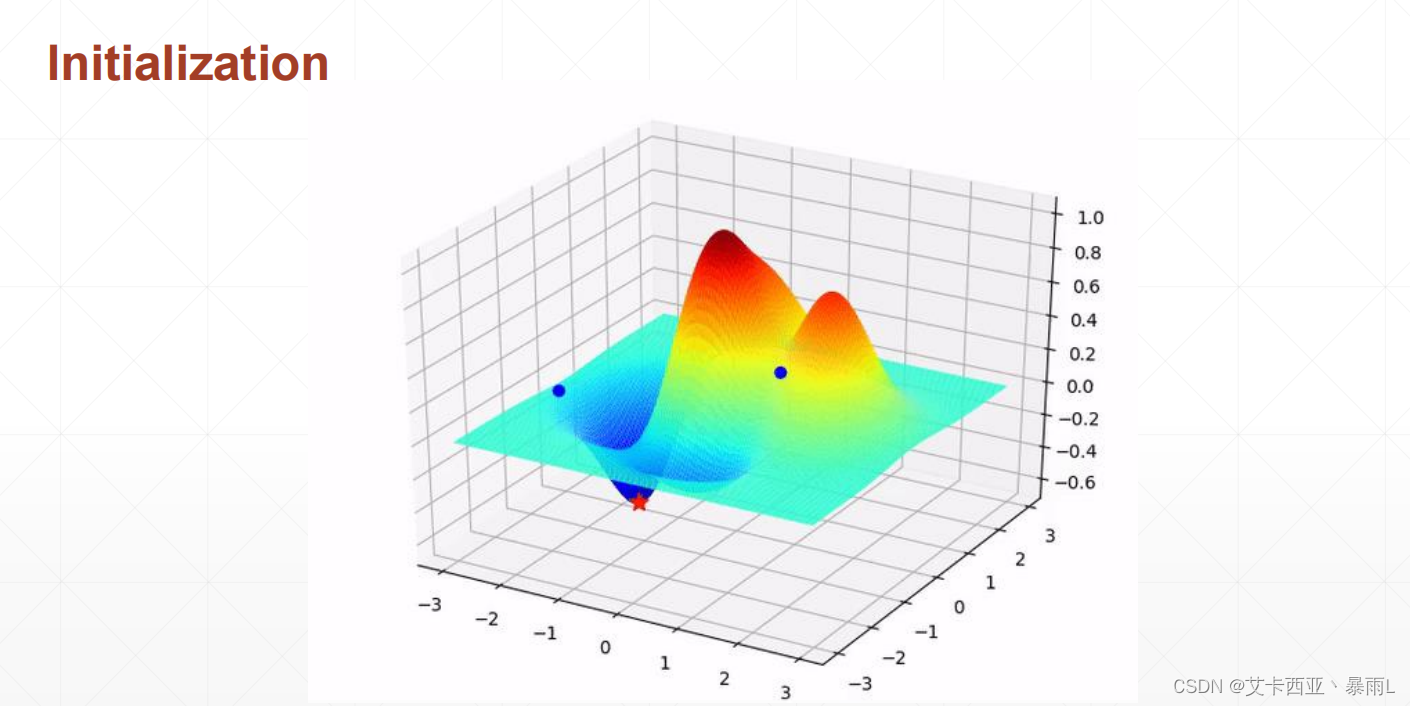
上图两种初始化,左边会到全局最小解,右边会到局部极小值,不同的初始化状态会得到不一样的结果
学习率
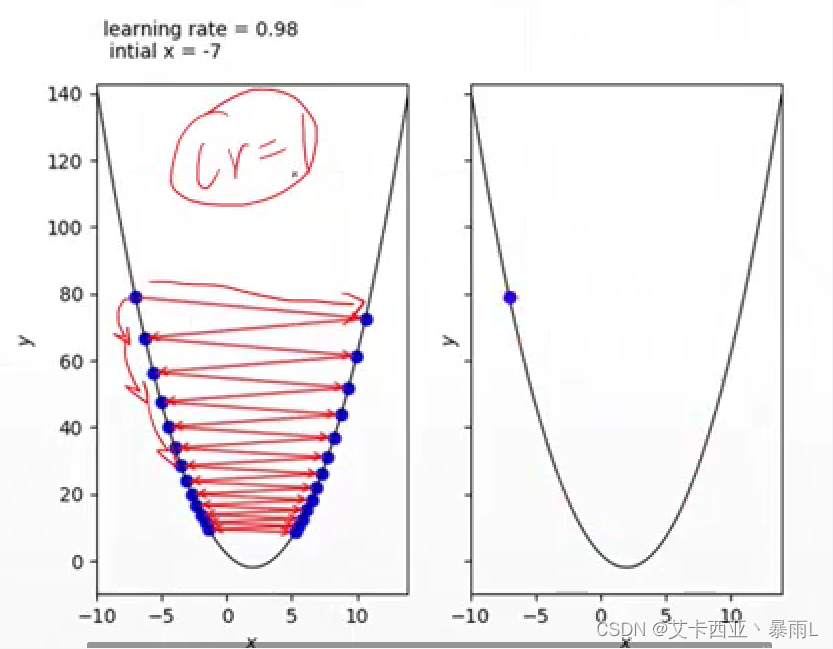
学习率设置为1的时候(比较大),步长会比较大,但实际上我们需要的情况是左边蓝色的点慢慢下降而不是左边跳到右边再跳到左边,是因为学习率设置的过大,会一步跨的太长直接跨过了最小值,对于比较好的函数还可以慢慢震荡到最小值,但是大部分现实情况是直接不收敛了,一开始要把learning rate设置的小一点,0.01或0.001这样,如果发现收敛了可以试着大一点这样会让收敛的速度会快一点
学习率也会影响收敛的精度,例如到最小值附近learning rate还是很大会一直在附近震动永远到不了最小值,只会得到一个近似比较好的情况,这种时候要慢慢减小learning rate
如何逃出局部最小值
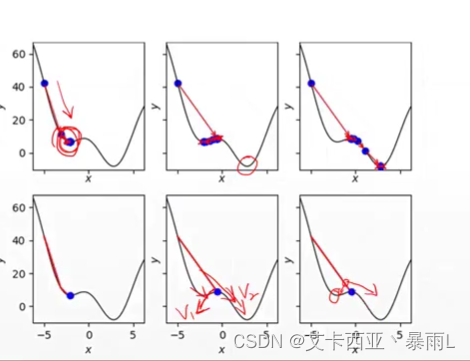
很有可能搜索到局部最小值就停止了,但是还有最小值,这时候可以添加一个动量,这个动量可以直观的理解为惯性,也就是说在局部极小值左边发现梯度呈现右下降的趋势,在右边发现梯度呈左下角的趋势,如果在此时考虑一个惯性的话,在右边的时候梯度会引导你回去到局部最小值,但是本来就是向右去降低梯度的,如果可以考虑到一个惯性的话,假设向右走是v1向量向左走是v2向量,把这两个向量综合一下就会得到一个朝向于偏向v2的方向
常见函数的梯度
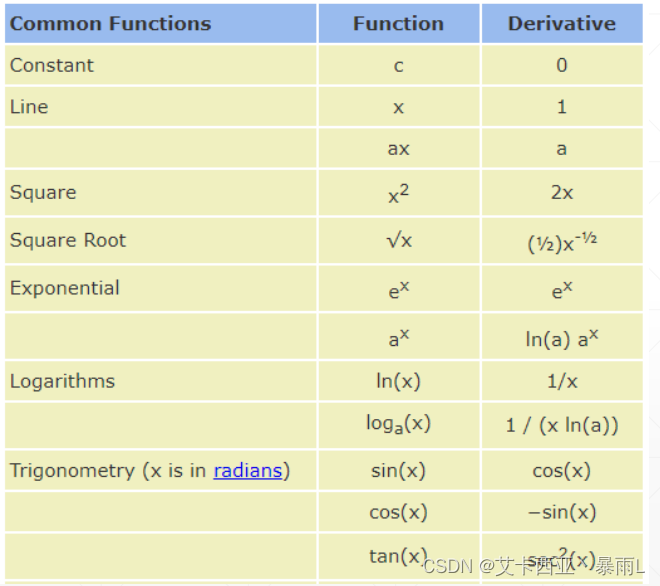
简单感知机线性模型的求解

二次模型的梯度

指数求解梯度的方式

线性感知机的输出和真实label之间的均方差

log函数求梯度
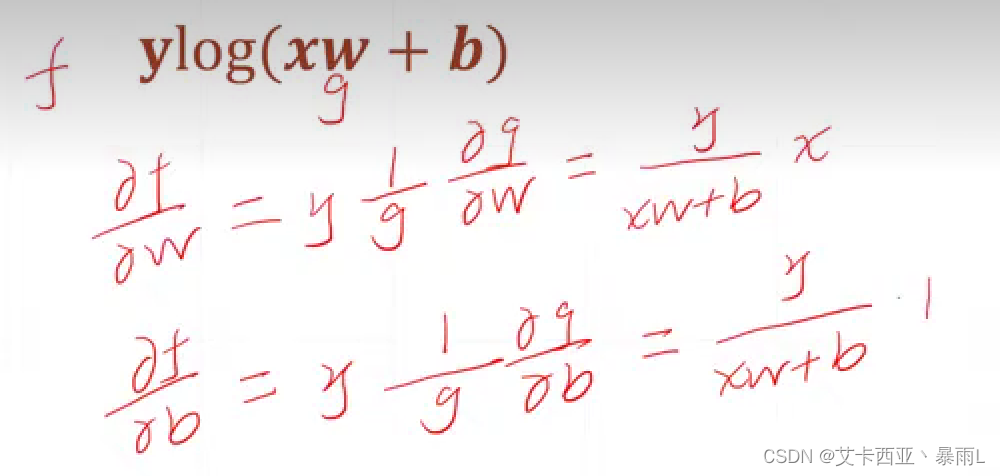
相关文章:
【pytorch12】什么是梯度
说明 导数偏微分梯度 梯度:是一个向量,向量的每一个轴是每一个方向上的偏微分 梯度是有方向也有大小,梯度的方向代表函数在当前点的一个增长的方向,然后这个向量的长度代表了这个点增长的速率 蓝色代表比较小的值,红色…...

南京,协同开展“人工智能+”行动
南京,作为江苏省的省会城市,一直以来都是科技创新和产业发展的高地。近日,南京市政府正式印发了《南京市进一步促进人工智能创新发展行动计划(2024—2026 年)》和《南京市促进人工智能创新发展若干政策措施》的“11”文…...
Selenium IDE 的使用指南
Selenium IDE 的使用指南 在自动化测试的领域中,Selenium 是一个广为人知且强大的工具集。而 Selenium IDE 作为其中的一个组件,为测试人员提供了一种便捷且直观的方式来创建和执行自动化测试脚本。 一、Selenium IDE 简介 Selenium IDE 是一个用于录…...

vue配置sql规则
vue配置sql规则 实现效果组件完整代码父组件 前端页面实现动态配置sql条件,将JSON结构给到后端,后端进行sql组装。 这里涉及的分组后端在组装时用括号将这块规则括起来就行,分组的sql连接符(并且/或者)取组里的第一个。…...

面试官:Redis执行lua脚本能保证原子性吗?
核心问题 Redis执行lua脚本是否能确保原子性? 面试经历 面试者在面试中自信回答Redis执行lua脚本能保证原子性,但未能深入解释原因。 原子性概念 原子性:一个事务的所有命令要么全部执行成功,要么全部执行失败。 Redis官方说…...

基于Chrome扩展的浏览器可信事件与网页离线PDF导出
基于Chrome扩展的浏览器可信事件与网页离线PDF导出 Chrome扩展是一种可以在浏览器中添加新功能和修改浏览器行为的软件程序,我们可以基于Manifest规范的API实现对于浏览器和Web页面在一定程度上的修改,例如广告拦截、代理控制等。Chrome DevTools Proto…...
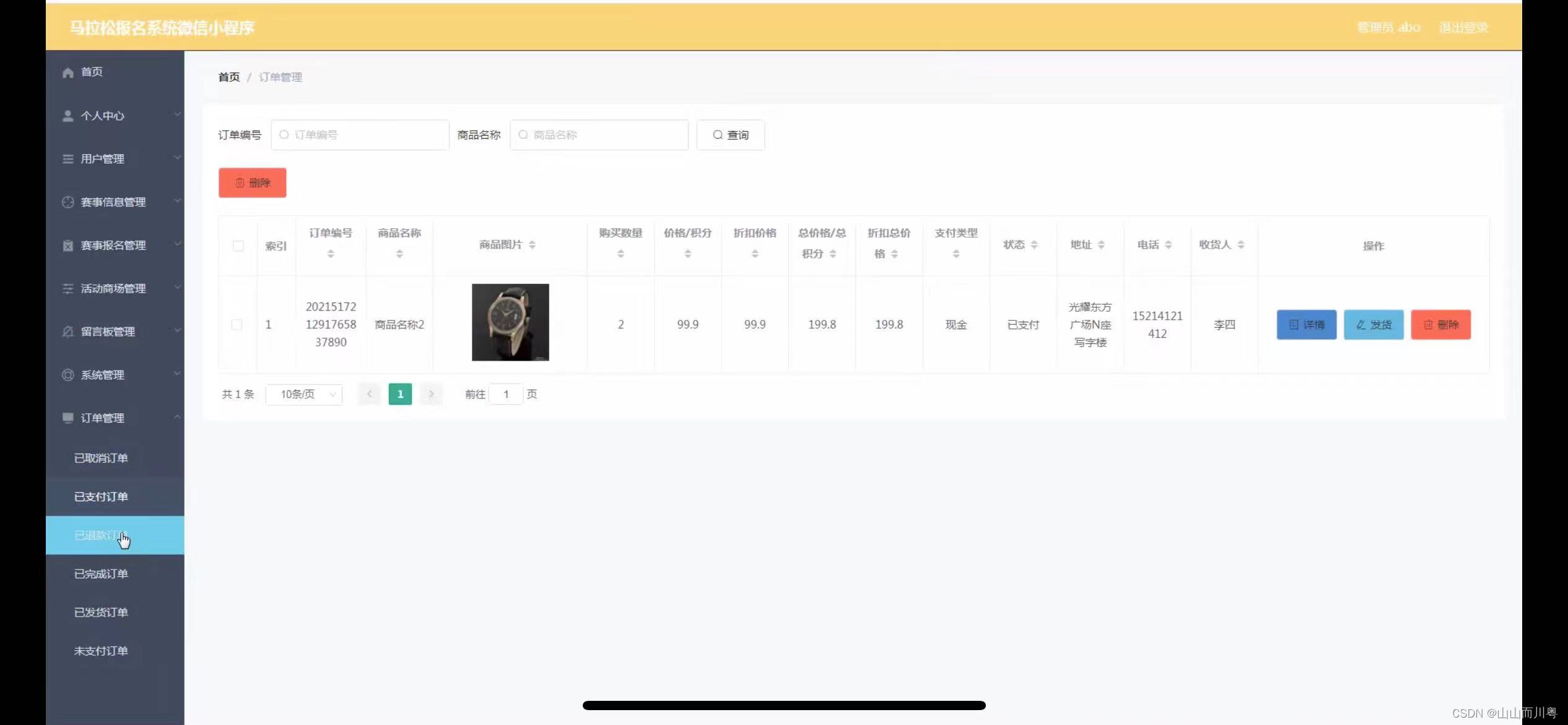
马拉松报名小程序的设计
管理员账户功能包括:系统首页,个人中心,用户管理,赛事信息管理,赛事报名管理,活动商城管理,留言板管理,系统管理 微信端账号功能包括:系统首页,赛事信息&…...
python使用pywebview集成vue3和element-plus开发桌面系统框架
随着web技术越来越成熟,就连QQ的windows客户端都用web技术来开发,所以在未来,web技术来开发windows桌面软件也会越来越多,所以在此发展驱动之下,将最近流程的python与web技术相结合,使用vue3和element-plus…...

C++线程的使用
C11之前,C语言没有对并发编程提供语言级别的支持,这使得我们在编写可移植的并发程序时,存在诸多的不便。现在C11中增加了线程以及线程相关的类,很方便地支持了并发编程,使得编写的多线程程序的可移植性得到了很大的提高…...

算法库应用--寻找最长麦穗
学习贺利坚老师算法库 数据结构例程——串的顺序存储应用_使用顺序串存储身份证号-CSDN博客 本人详细解析博客 串的顺序存储的应用实例二_串的顺序存储应用-CSDN博客 版本更新日志 V1.0: 在原有的基础上, 进行优化名字, 并且有了相应的算法库作为支撑, 我使用了for循环来代替老…...

ython 使用 cx_Freeze 打包,不想要打包文件中能直接看到依赖的代码,如何处理
背景:因为使用 cx_Freeze 打包时,添加需要依赖的文件 cx_Freeze 是一个用于将 Python 程序打包成独立可执行文件的工具,支持多个平台。当你需要打包包含多个 .py 文件的项目时,你可以通过编写一个 setup.py 文件来指定哪些模块应…...

某DingTalk企典 - Token
⚠️前言⚠️ 本文仅用于学术交流。 学习探讨逆向知识,欢迎私信共享学习心得。 如有侵权,联系博主删除。 请勿商用,否则后果自负。 网址 aHR0cHM6Ly9kaW5ndGFsay5jb20vcWlkaWFuLw 浅聊一下 没毛病,就这字段,有效期…...
手写一个类似@RequestParam的注解(用来接收请求体的参数)
一、本文解决的痛点 按照大众认为的开发规范,一般post类型的请求参数应该传在请求body里面。但是我们有些post接口只需要传入一个字段,我们接受这种参数就得像下面这样单独创建一个类,类中再添加要传入的基本类型字段,配合Reques…...

【遇坑笔记】Node.js 开发环境与配置 Visual Studio Code
【遇坑笔记】Node.js 开发环境与配置 Visual Studio Code 前言node.js开发环境配置解决pnpm 不是内部或外部命令的问题(pnpm安装教程)解决 pnpm : 无法加载文件 C:\Program Files\nodejs\pnpm.ps1,因为在此系统上禁止运行脚本。 vscode 插件开…...

【ajax实战07】文章筛选功能
本文章目标:根据筛选条件,获取匹配数据展示 本章**“查询参数对象”指的是,要“获取文章列表”功能**中服务器接口要求配置的对象 实现步骤如下: 一:设置频道列表数据 二:监听筛选条件改变,…...

promise.all和promise.race的区别
Promise.all和Promise.race是JavaScript中Promise API的两个重要方法,它们在处理多个Promise对象时表现出不同的行为。以下是它们之间的主要区别: 1. 功能和行为 Promise.all: 功能:接收一个包含多个Promise的数组&#x…...
Python爬取豆瓣电影+数据可视化,爬虫教程!
1. 爬取数据 1.1 导入以下模块 import os import re import time import requests from bs4 import BeautifulSoup from fake_useragent import UserAgent from openpyxl import Workbook, load_workbook1.2 获取每页电影链接 def getonepagelist(url,headers):try:r reque…...

初阶数据结构二叉树练习系列(1)
这个系列的文章将带大家一起刷题,并且总结思路 温馨提示:本篇文章里的练习题仅适合刚学完二叉树的小白使用 相同的树 思路 情况分析:第一种情况:两棵树都为空 → 返回true 第二种情况&am…...

【selenium 】操作元素
操作元素 元素操作鼠标操作键盘操作 元素操作 元素操作示例清空输入框clear()deiver.find_element_by_id(“username”).clear()输入文字send_keys()deiver.find_element_by_id(“username”).send_keys(‘zs’)元素点击 click()deiver.find_element_by_id(“login”).click()…...
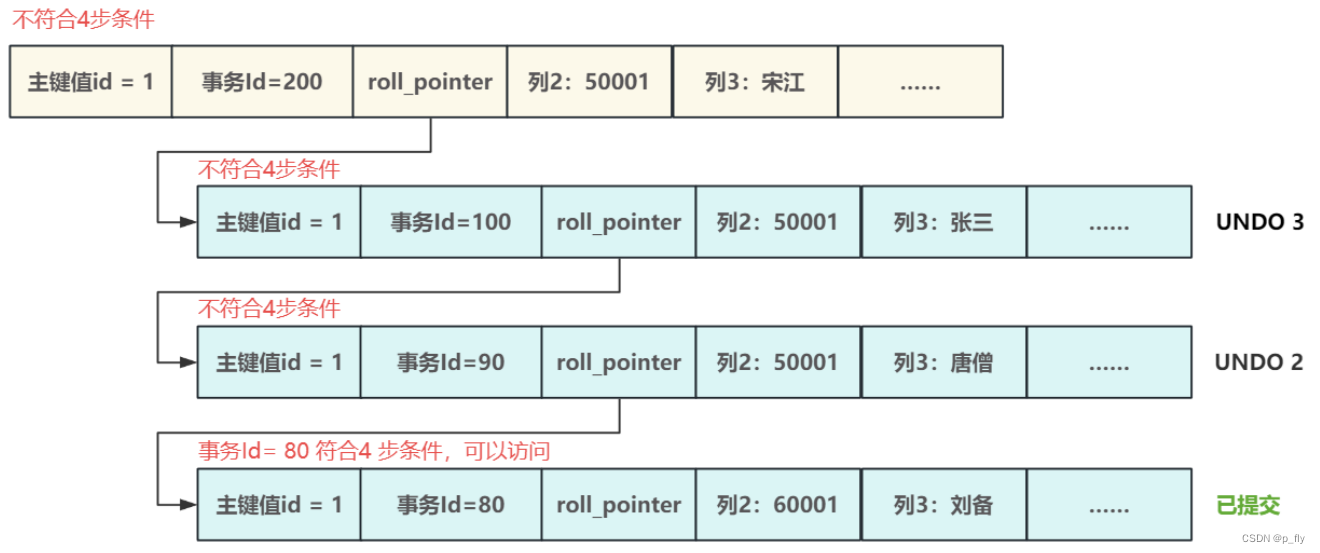
【MySQL】事务实现原理
目录 事务 如何使用 ACID 原子性(Atomicity) 原子性实现原理 持久性(Durability) 持久性实现原理 隔离性 隔离级别 读未提交 读已提交 可重复读 串行化 隔离级别原理 锁 共享锁&独占锁 意向锁 索引记录锁 间隙锁 临键锁 插入意向锁 自增锁 MVCC 实现…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
