【Linux系统】CUDA的安装与graspnet环境配置遇到的问题
今天在安装环境时遇到报错:
The detected CUDA version (10.1) mismatches the version that was used to compile
PyTorch (11.8). Please make sure to use the same CUDA versions.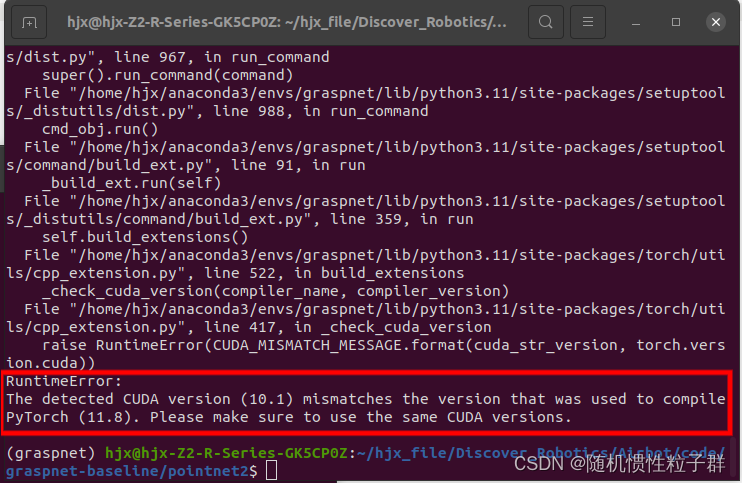
报错原因:安装的cuda版本不对应,我需要安装cuda的版本为11.8
下面开始cuda的安装:
1.打开网址CUDA Toolkit Archive | NVIDIA Developer![]() https://developer.nvidia.com/cuda-toolkit-archive
https://developer.nvidia.com/cuda-toolkit-archive
2.下载11.8版本就点击CUDA Toolkit 11.8,如下图:
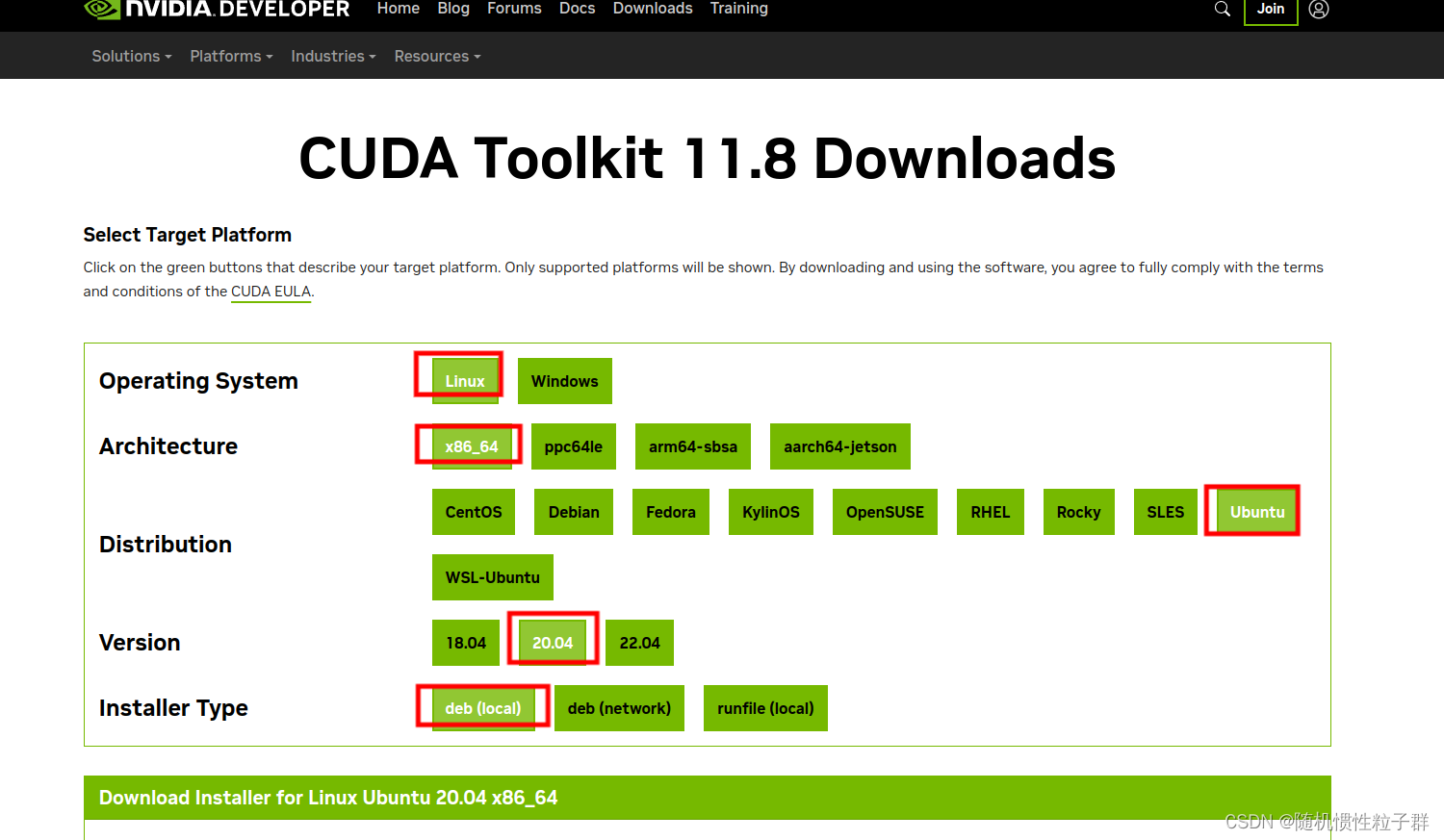
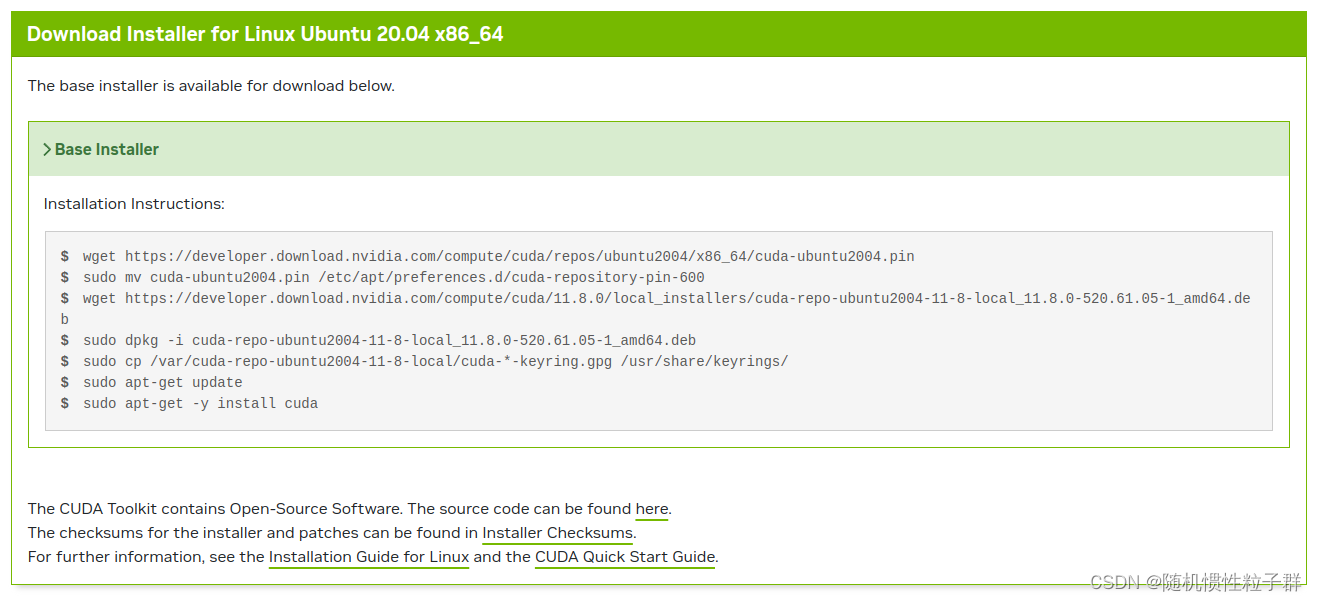
按照指令依次执行即可
在安装环境期间,遇到如下报错:
error: [Errno 2] No such file or directory: '/usr/local/cuda/bin/nvcc'
如果 /usr/local/cuda 是指向当前活跃 CUDA 版本的符号链接,确保它链接到了正确的版本:
如果链接不正确,你可以通过以下命令更新它:
sudo ln -sfn /usr/local/cuda-11.8 /usr/local/cuda
还遇到了:
error: command '/usr/bin/gcc' failed with exit code 1
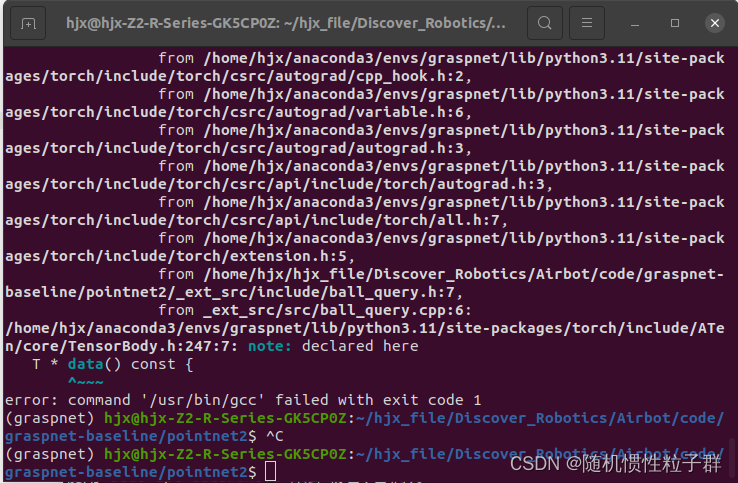
原因是conda环境中的python版本过高,降低python版本为3.9即可
在环境安装时发现numpy的版本也过高了,正确的版本如下:
pip install numpy==1.23.0
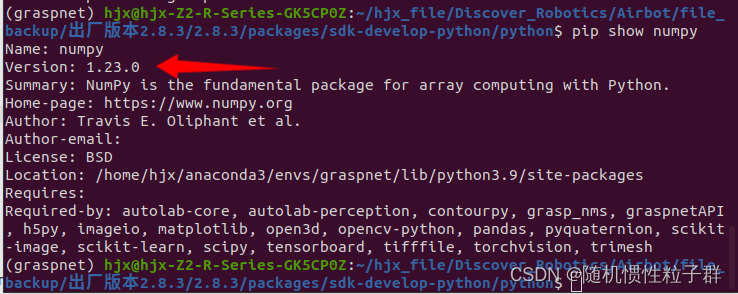
后来又遇到了报错:
ImportError: libcudart.so.12: cannot open shared object file: No such file or directory

应该时cuda11.8的版本问题,我后面又换成了cuda12.1版本,对应的pytorch版本也需要进行适配
注意torch的版本要降低为2.1.0:
[linux] undefined symbol: _ZN2at4_ops5zeros4callEN3c108ArrayRefINS2_6SymIntEEENS2_8optionalINS2_10Sc-CSDN博客
补充:解压2.8.3版本包里Packages文件下的sdk-develop-python包的指令
sudo apt install libspdlog-dev
python setup.py install
相关文章:

【Linux系统】CUDA的安装与graspnet环境配置遇到的问题
今天在安装环境时遇到报错: The detected CUDA version (10.1) mismatches the version that was used to compile PyTorch (11.8). Please make sure to use the same CUDA versions. 报错原因:安装的cuda版本不对应,我需要安装cuda的版本…...
滤波算法学习笔记
目录 引言 一、定义 二、分类 三、常见滤波算法 四、应用与优势 五、发展趋势 例程 1. 均值滤波(Moving Average Filter) 2. 中值滤波(Median Filter) 3. 高斯滤波(Gaussian Filter) 4.指数移动…...
【机器学习】机器学习的重要方法——线性回归算法深度探索与未来展望
欢迎来到 破晓的历程博客 引言 在数据科学日益重要的今天,线性回归算法以其简单、直观和强大的预测能力,成为了众多领域中的基础工具。本文将详细介绍线性回归的基本概念、核心算法,并通过五个具体的使用示例来展示其应用,同时探…...

百度云智能媒体内容分析一体机(MCA)建设
导读 :本文主要介绍了百度智能云MCA产品的概念和应用。 媒体信息海量且复杂,采用人工的方式对视频进行分析处理,面临着效率低、成本高的困难。于是,MCA应运而生。它基于百度自研的视觉AI、ASR、NLP技术,为用户提供音视…...

笔记本电脑部署VMware ESXi 6.0系统
正文共:888 字 18 图,预估阅读时间:1 分钟 前面我们介绍了在笔记本上安装Windows 11操作系统(Windows 11升级不了?但Win10就要停服了啊!来,我教你!),也介绍了…...
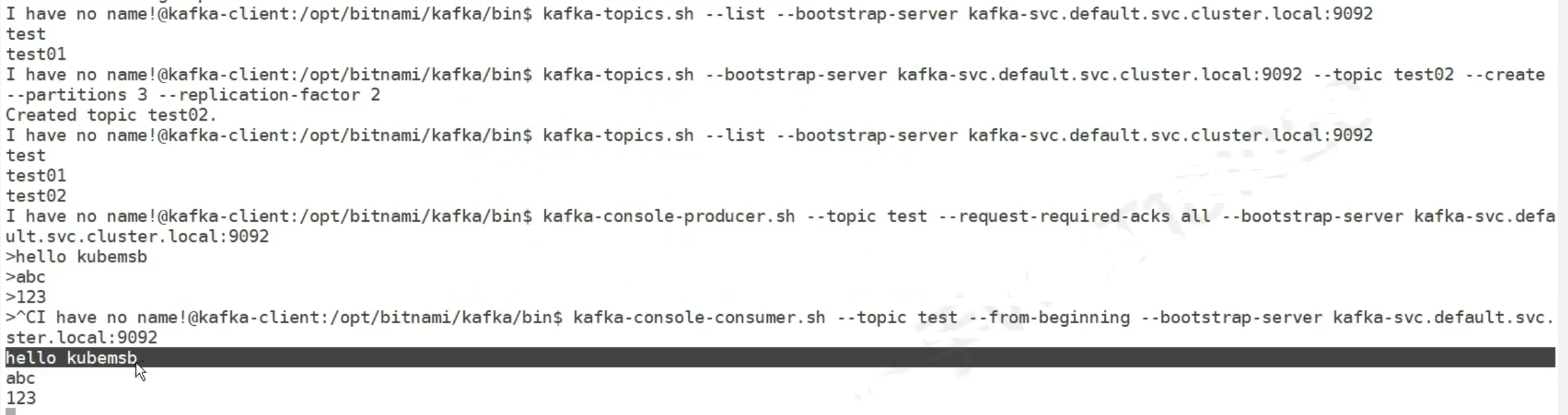
k8s 中间件
1. zookeeper 是的,Zookeeper 和 Kafka 经常一起使用,Zookeeper 在 Kafka 中扮演了关键角色。以下是 Zookeeper 和 Kafka 在实际项目中的结合使用及其作用的详细说明。 项目背景 假设我们有一个分布式数据处理系统,该系统需要高吞吐量的实…...

如何 提升需求确定性
提升需求确定性是确保项目成功的关键之一。以下是一些方法和策略可以帮助你提升需求的确定性: 积极的利益相关者参与: 确保所有关键利益相关者(包括最终用户、业务所有者、开发团队等)参与需求收集和确认过程。他们的参与可以提供…...

探索Sui的面向对象模型和Move编程语言
Sui区块链作为一种新兴的一层协议(L1),采用先进技术来解决常见的一层协议权衡问题。Cointelegraph Research详细剖析了这一区块链新秀。 Sui使用Move编程语言,该语言专注于资产表示和访问控制。本文探讨了Sui的对象中心数据存储模…...

【vue动态组件】VUE使用component :is 实现在多个组件间来回切换
VUE使用component :is 实现在多个组件间来回切换 component :is 动态父子组件传值 相关代码实现: <component:is"vuecomponent"></component>import componentA from xxx; import componentB from xxx; import componentC from xxx;switch(…...
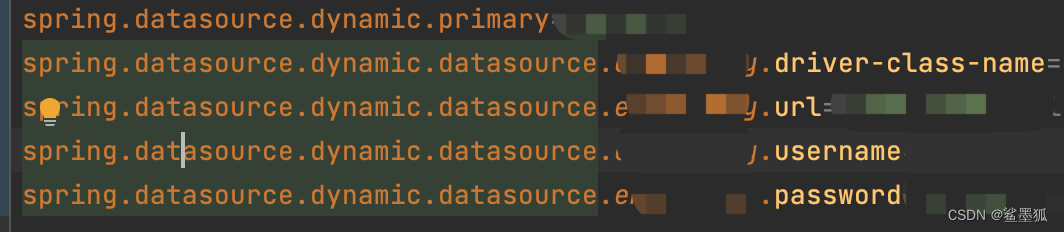
springboot dynamic配置多数据源
pom.xml引入jar包 <dependency><groupId>com.baomidou</groupId><artifactId>dynamic-datasource-spring-boot-starter</artifactId><version>3.5.2</version> </dependency> application配置文件配置如下 需要主要必须配置…...
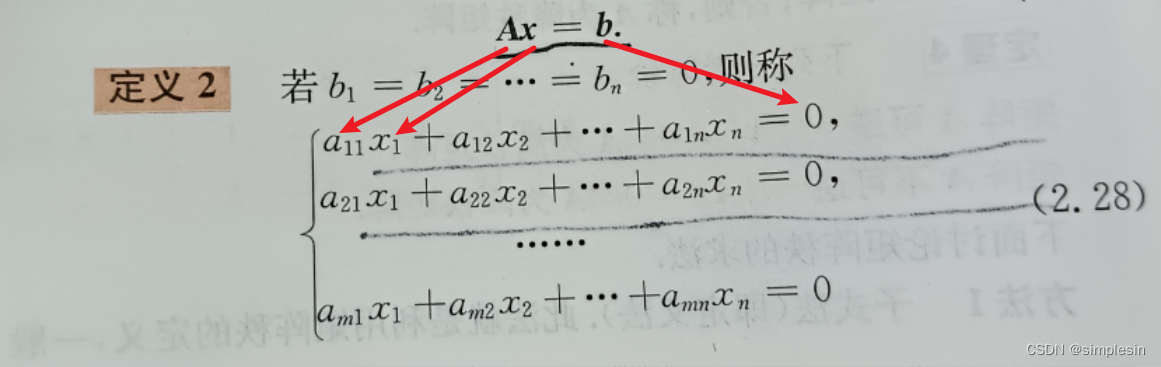
线性代数知识点搜刮
求你别考太细... 目录 异乘变零定理 行列式转置 值不变 重要关系 中间相等,取两头 特征值公式 向量正交 点积为0 拉普拉斯定理 矩阵的秩 特征值和特征向量 |A|特征值的乘积 & tr(A)特征值的和 要记要背 增广矩阵 异乘变零定理 某行(…...

景区智能厕所系统,打造智能化,人性化公共空间
在智慧旅游的大潮中,景区智能厕所系统正逐渐成为提升公共空间智能化、人性化水平的关键载体。作为智慧城市建设的重要组成部分,智能厕所系统不仅解决了传统公厕存在的诸多问题,更通过科技的力量,为游客创造了更加舒适、便捷的如厕…...

Windows中Git的使用(2024最新版)
Windows中Git的使用 获取ssh keys本地绑定邮箱初始化本地仓库添加到本地缓存区提交到本地缓存区切换本地分支为main关联远程分支推送到GitHub查看推送日志 Git 2020年发布了新的默认分支名称"main",取代了"master"作为主分支的名称。操作有了些…...
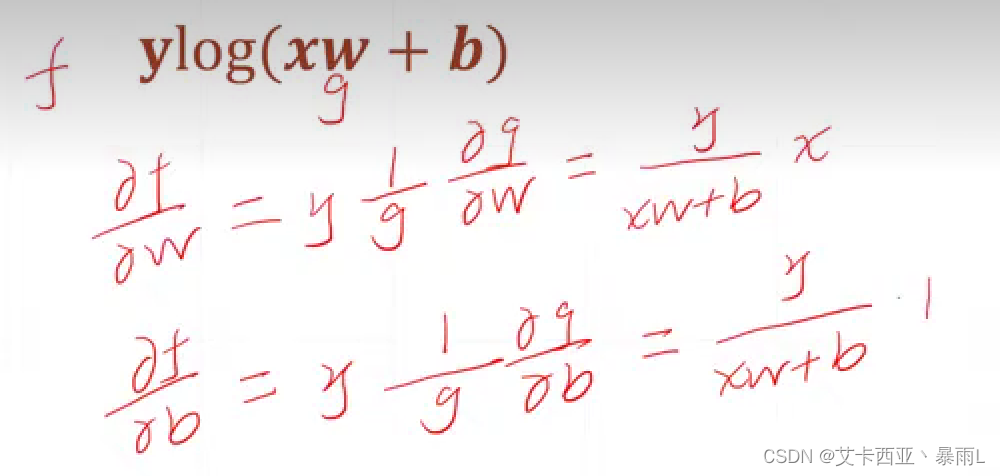
【pytorch12】什么是梯度
说明 导数偏微分梯度 梯度:是一个向量,向量的每一个轴是每一个方向上的偏微分 梯度是有方向也有大小,梯度的方向代表函数在当前点的一个增长的方向,然后这个向量的长度代表了这个点增长的速率 蓝色代表比较小的值,红色…...

南京,协同开展“人工智能+”行动
南京,作为江苏省的省会城市,一直以来都是科技创新和产业发展的高地。近日,南京市政府正式印发了《南京市进一步促进人工智能创新发展行动计划(2024—2026 年)》和《南京市促进人工智能创新发展若干政策措施》的“11”文…...
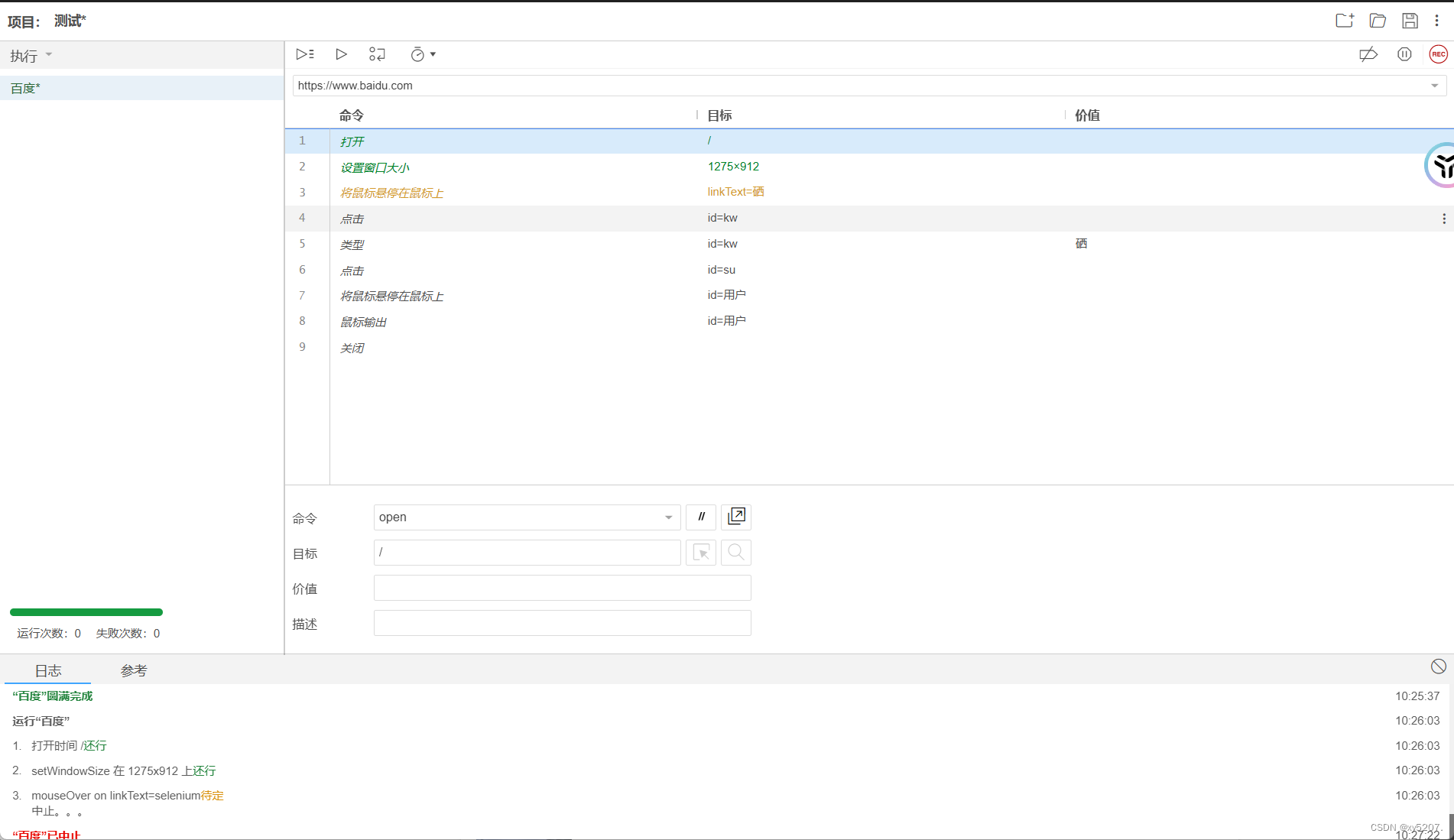
Selenium IDE 的使用指南
Selenium IDE 的使用指南 在自动化测试的领域中,Selenium 是一个广为人知且强大的工具集。而 Selenium IDE 作为其中的一个组件,为测试人员提供了一种便捷且直观的方式来创建和执行自动化测试脚本。 一、Selenium IDE 简介 Selenium IDE 是一个用于录…...

vue配置sql规则
vue配置sql规则 实现效果组件完整代码父组件 前端页面实现动态配置sql条件,将JSON结构给到后端,后端进行sql组装。 这里涉及的分组后端在组装时用括号将这块规则括起来就行,分组的sql连接符(并且/或者)取组里的第一个。…...

面试官:Redis执行lua脚本能保证原子性吗?
核心问题 Redis执行lua脚本是否能确保原子性? 面试经历 面试者在面试中自信回答Redis执行lua脚本能保证原子性,但未能深入解释原因。 原子性概念 原子性:一个事务的所有命令要么全部执行成功,要么全部执行失败。 Redis官方说…...

基于Chrome扩展的浏览器可信事件与网页离线PDF导出
基于Chrome扩展的浏览器可信事件与网页离线PDF导出 Chrome扩展是一种可以在浏览器中添加新功能和修改浏览器行为的软件程序,我们可以基于Manifest规范的API实现对于浏览器和Web页面在一定程度上的修改,例如广告拦截、代理控制等。Chrome DevTools Proto…...
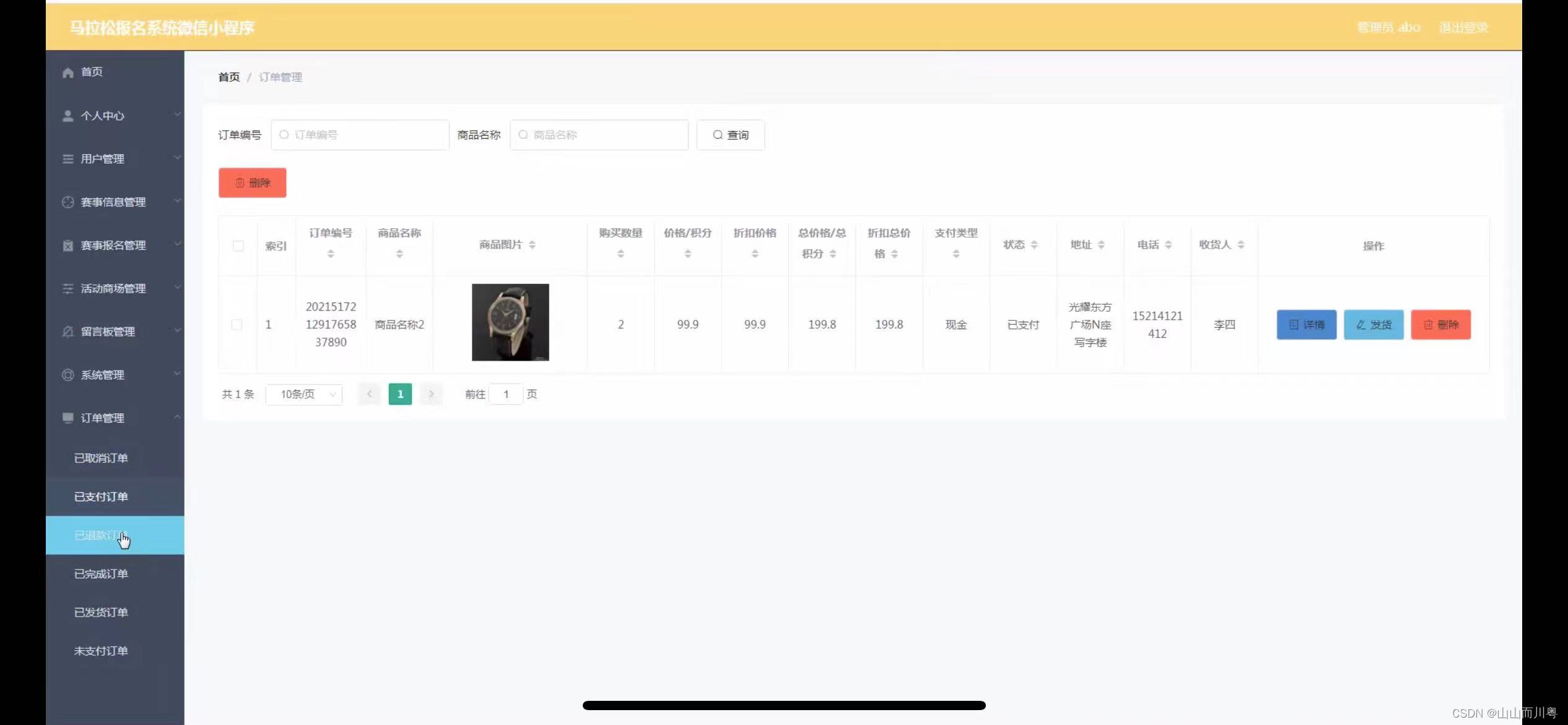
马拉松报名小程序的设计
管理员账户功能包括:系统首页,个人中心,用户管理,赛事信息管理,赛事报名管理,活动商城管理,留言板管理,系统管理 微信端账号功能包括:系统首页,赛事信息&…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
