点估计和参数分布的对比
点估计(Point Estimation)和 参数分布(Parameter Distribution)是统计学中两种不同的参数估计方法。
文章目录
- 点估计(Point Estimation)
- 参数分布(Parameter Distribution)
- 对比总结
点估计(Point Estimation)
定义:
点估计是指使用样本数据来估计总体参数的一个单一值。这个单一值被称为估计量(Estimator),而它的具体数值被称为估计值(Estimate)。点估计的目的是找到一个最能代表总体参数的数值。
常见方法:
- 极大似然估计(MLE): 找到使得观测数据出现概率最大的参数值。
- 矩估计(Method of Moments): 通过匹配样本矩(如均值、方差)和总体矩来估计参数。
- 最小二乘估计(Least Squares Estimation): 在回归分析中,通过最小化预测值和实际值之间的平方和来估计参数。
特点:
- 简单直观: 点估计提供了一个明确的数值,易于理解和解释。
- 缺乏不确定性信息: 点估计没有提供关于估计值不确定性的信息。
参数分布(Parameter Distribution)
定义:
参数分布是指参数的整个概率分布,而不是单一的数值。在贝叶斯统计中,参数被视为随机变量,具有一定的概率分布。参数分布反映了我们对参数的所有可能值及其相应概率的信念。
常见方法:
- 贝叶斯估计: 结合先验分布和数据,通过贝叶斯定理计算参数的后验分布。
- Bootstrap方法: 通过从样本中重复抽样,构建参数的经验分布。
特点:
- 提供不确定性信息: 参数分布提供了关于参数估计的不确定性信息,如置信区间、可信区间等。
- 灵活性: 参数分布可以用于计算各种统计量,如均值、中位数、众数等。
对比总结
- 结果形式: 点估计提供一个单一的数值,而参数分布提供一个完整的概率分布。
- 不确定性信息: 点估计不提供不确定性信息,而参数分布提供了关于参数估计的不确定性。
- 应用场景: 点估计适用于需要一个明确答案的场景,而参数分布适用于需要考虑参数不确定性的场景。
相关文章:

点估计和参数分布的对比
点估计(Point Estimation)和 参数分布(Parameter Distribution)是统计学中两种不同的参数估计方法。 文章目录 点估计(Point Estimation)参数分布(Parameter Distribution)对比总结 …...
桌面保存的Word文件删除怎么找回?超实用的三个方法?
在日常工作和学习中,我们经常会使用Word文档进行文字编辑和文件保存。但是,有时由于操作失误或系统故障,我们会不小心将存放在电脑桌面重要的Word文件删除了。导致无法挽回的损失,但幸运的是,有一些方法可以帮助我们找…...

【leetcode】双指针算法题
文章目录 1.算法思想2.移动零3.复写零方法一方法二 4.快乐数5.盛水最多的容器方法一(暴力求解)方法二(左右指针) 6.有效三角形的个数方法一(暴力求解)方法二(左右指针) 7.两数之和8.…...

vue-router 源码分析——8.重定向
这是对vue-router 3 版本的源码分析。 本次分析会按以下方法进行: 按官网的使用文档顺序,围绕着某一功能点进行分析。这样不仅能学习优秀的项目源码,更能加深对项目的某个功能是如何实现的理解。这个对自己的技能提升,甚至面试时…...

CAN总线协议
CAN总线协议,全程为控制器局域网(Controller Area Network)协议,是一种用于实时应用的串行通讯协议。该协议由德国某公司专门为汽车行业开发,并逐渐成为一种标准,这是国际上应用最广泛的现场总线之一。 一…...
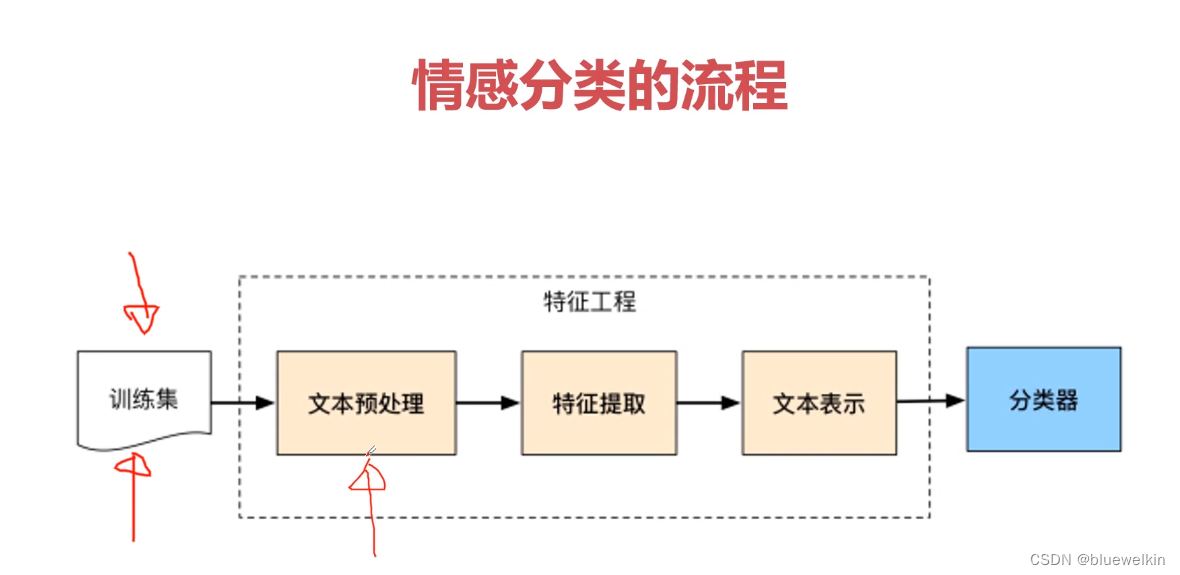
NLP篇1
场景:假设给你一篇文章。 目标:说白了,就是数学的分类。但是如何实现分类呢。下面将逐步一 一 分析与拆解。先把目标定好了和整体框架定好了。而不是只见树木而不见森林。 情感分类(好评、差评,中性) 整体…...

【一念发动便是行】念头,就是命运
一个个恶念累积就是负能量,念头就是命运,克除恶念,防范念头,念头都有能量,学圣学须内外庄严检肃,言语有灵 多数人的问题都是出在念头上,念头,就是自己的命运; 当我们对自…...

Django + Vue 实现图片上传功能的全流程配置与详细操作指南
文章目录 前言图片上传步骤1. urls 配置2. settings 配置3. models 配置4. 安装Pillow 前言 在现代Web应用中,图片上传是一个常见且重要的功能。Django作为强大的Python Web框架,结合Vue.js这样的现代前端框架,能够高效地实现这一功能。本文将…...

【介绍下R-tree,什么是R-tree?】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...
)
每天10个js面试题(二)
1.事件轮询? JavaScript 是单线程的,同一时间只能做一件事。所有任务都需要排队,前一个任务结束,才会执行后一个任务,为了保证任务有序的执行,事件轮询就是单线程任务调度的一种方式,单线程任务…...

深入理解【 String类】
目录 1、String类的重要性 2、常用方法 2、1 字符串构造 2、2 String对象的比较 2、3 字符串查找 2、4字符转换 数值和字符串转换: 大小写转化: 字符串转数组: 格式转化: 2、5 字符串替换 2、6字符串拆分 2、7 字符串…...
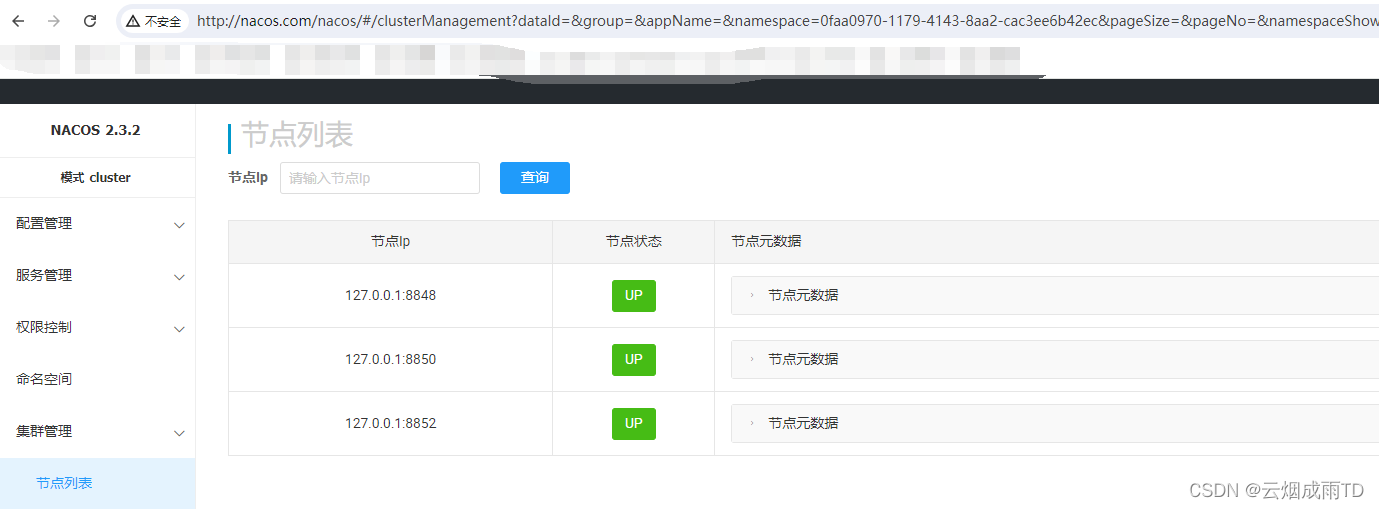
Nacos 2.x 系列【20】集群部署
文章目录 1. 前言2. 部署服务端2.1 准备工作2.2 集群节点配置2.3 鉴权配置2.4 配置数据源2.5 配置 IP2.6 配置端口2.7 启动集群 3. 部署模式3.1 直连模式3.2 地址服务器模式3.2.1 地址服务器3.2.2 配置 3.3 VIP 模式(推荐)3.3.1 Nginx3.3.1 域名 1. 前言…...

LeetCode刷题记录:(15)三角形最小路径和
知识点:倒叙的动态规划 题目传送 解法一:二维动态规划【容易理解】 class Solution {public int minimumTotal(List<List<Integer>> triangle) {int n triangle.size();if (n 1) {return triangle.get(0).get(0);}// dp[i][j]:走到第i层第…...

【大数据面试题】35 Spark 怎么做优化?
一步一个脚印,一天一道大数据面试题 博主希望能够得到大家的点赞收,藏支持!非常感谢~ 点赞,收藏是情分,不点是本分。祝你身体健康,事事顺心! Spark 如何做优化一直是面试过程中常问的问题。那么这次也仅以此篇文章总结梳理,希望对大家有帮助。 通用优化 Spark 一般遇…...

2024年保安员职业资格考试题库大数据揭秘,冲刺高分!
186.安全技术防范是一种由探测、()、快速反应相结合的安全防范体系。 A.保安 B.出警 C.延迟 D.监控 答案:C 187.安全技术防范是以()和预防犯罪为目的的一项社会公共安全业务。 A.预防灾害 B.预防损失 C.预防失…...

怎么搭建个人博客教程,附云主机选购指南
一、搭建个人博客教程 1. 规划博客内容与技术栈 确定博客主题:首先明确博客的定位和主题,这将影响后续的技术选择和内容规划。选择技术栈:根据个人偏好和技术背景,选择合适的建站技术。例如,可以使用WordPress&#…...

使用Llama3/Qwen2等开源大模型,部署团队私有化Code Copilot和使用教程
目前市面上有不少基于大模型的 Code Copilot 产品,部分产品对于个人开发者来说可免费使用,比如阿里的通义灵码、百度的文心快码等。这些免费的产品均通过 API 的方式提供服务,因此调用时均必须联网、同时需要把代码、提示词等内容作为 API 的…...
)
C语言_结构体初阶(还未写完)
结构体的声明 1. 什么是结构?结构是一些值的集合,这些值称为成员变量。结构的每个成员可以是不同类型的变量 数组:一组相同类型元素的集合 结构体:一组不一定相同类型元素的集 2. 结构的声明 struct tag //tag根据实际情况给名字…...

MyBatis-Plus:快速入门
1. 概念 MyBatis-Plus(简称 MP)是一个MyBatis 的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效率而生。其突出的特性如下: * **无侵入**:只做增强不做改变,引入它不会对现有…...
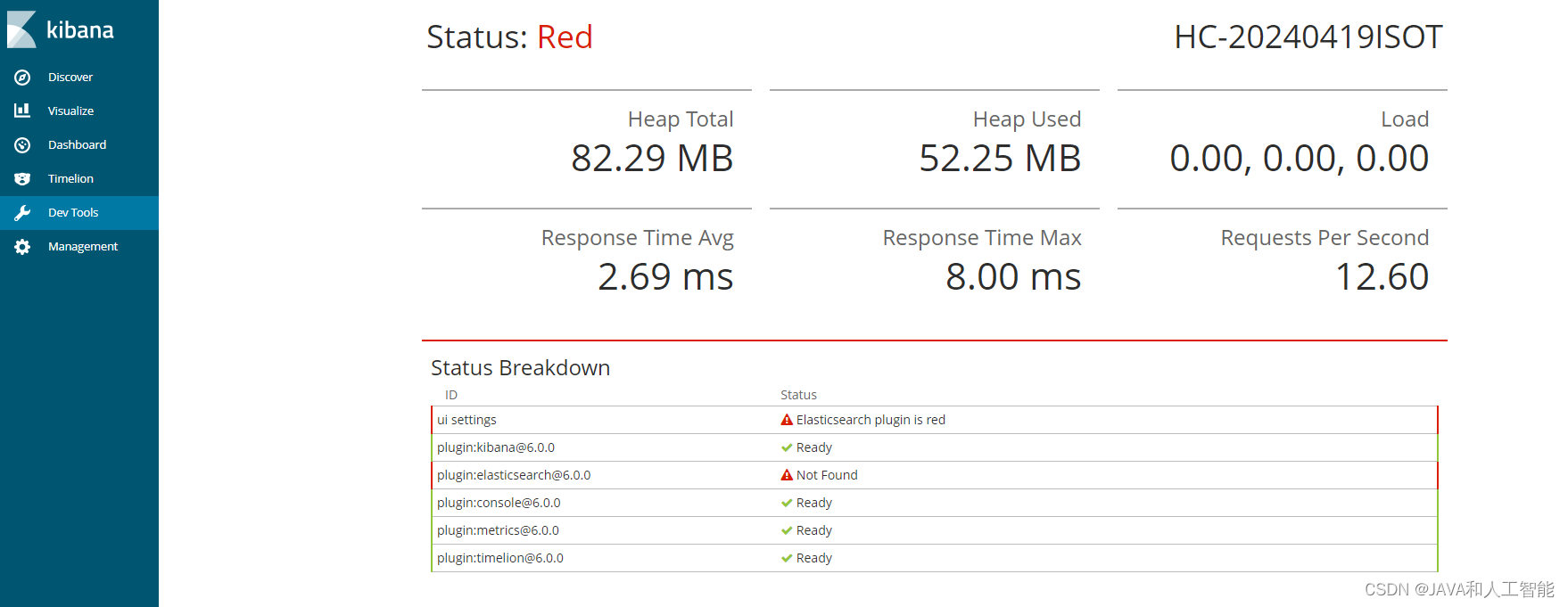
【高级篇】第9章 Elasticsearch 监控与故障排查
9.1 引言 在现代数据驱动的应用架构中,Elasticsearch不仅是海量数据索引和搜索的核心,其稳定性和性能直接影响到整个业务链路的健康度。因此,建立有效的监控体系和掌握故障排查技能是每一位Elasticsearch高级专家的必备能力。 9.2 监控工具:洞察与优化的利器 在Elastics…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
