(数论)(枚举)(前缀和)1230. K倍区间
目录
题目链接
一些话
切入点
流程
套路
ac代码
题目链接
1230. K倍区间 - AcWing题库
~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,
一些话
相似题型:隐藏的牛
NYIST(计科ACM&TC)第三次招新赛_栞那Kanna的博客-CSDN博客
~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,
切入点
如果其中一段连续的子序列 Ai,Ai+1,…Aj 之和是 K 的倍数,我们就称这个区间 [i,j]是 K 倍区间。
你能求出数列中总共有多少个 K 倍区间吗?
求有多少个类问题,符合枚举的特征
求区间和问题,符合前缀和特征~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,
流程
1.看数据范围
数据范围
1≤N,K≤100000;
1≤Ai≤100000
n = 1e6,就算是区间枚举也会超时,O((n+1)*(n/2))
所以只能单重循环枚举
2.读题寻找条件
题目要求 区间和%k==0
即(s[i] - s[j-1] ) % k == 0
这需要双循环枚举两个点
此时开始想能不能把点拆开来,枚举一个就得到另一个
拆分公式
((s[i] % k) - (s[j-1] % k ) + k) % k == 0(这是一般的减法取余)
因为i与j-1的组合等价于j-1与i的组合,所以这两个值可以互相调换成差值大于0
的情况,此时就可以直接写成s[i] % k == s[j-1] % k;
枚举的时候只要s[i]%k的结果相同,就可以组成一个符合要求的区间。
所以就用类似牛腿问题的计数方法
ans += cnt[s[i]%k];
cnt[s[i]%k]++;
此外如果s[i] 自身%k== 0也要计数
cnt[s[i]%k] = 1,就可以让这种情况每次计入ans时比其他情况多1
套路
求情况数量题
一个数组、字符串内的元素是特殊的某种情况,组合可以形成满足题意的情况:
元素可以任意两两组合:
用一重循环
cnt统计当前特殊情况元素数量
if(特殊情况出现){
res += cnt;,
cnt++;
}
这是用前面出现的特殊情况元素和当前新出现的一个特殊情况元素组合,从而新组合成cnt种满足题意的情况
ac代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1e5 + 10;
int cnt[N];
long long f[N];
int main(){int n,k;cin >> n >> k;for(int i = 1;i <= n;i++) {scanf("%lld",&f[i]);f[i] += f[i-1];}cnt[0] = 1;long long ans = 0;for(int i = 1;i <=n;i++){ans += cnt[f[i]%k];cnt[f[i]%k]++;}cout << ans << endl;return 0;
}我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!
相关文章:
(枚举)(前缀和)1230. K倍区间)
(数论)(枚举)(前缀和)1230. K倍区间
目录 题目链接 一些话 切入点 流程 套路 ac代码 题目链接 1230. K倍区间 - AcWing题库 ~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水&…...

万字带你深入理解 Linux 虚拟内存管理(下)
接上文:万字带你深入理解 Linux 虚拟内存管理(上) 6. 程序编译后的二进制文件如何映射到虚拟内存空间中 经过前边这么多小节的内容介绍,现在我们已经熟悉了进程虚拟内存空间的布局,以及内核如何管理这些虚拟内存区域&…...

【iOS】—— JSONModel源码学习
JSONModel 文章目录JSONModel关于JSONModel的用法initWithDictionary等方法load方法实现load方法调用时机init方法__setup__方法__inspectProperties:方法__doesDictionary方法__importDictionary方法关于JSONModel的用法 可以参考之前写的博客:【iOS】—— JSONMo…...
单片机怎么实现真正的多线程?
所谓多线程都是模拟的,本质都是单线程,因为cpu同一时刻只能执行一段代码。模拟的多线程就是任务之间快速切换,看起来像同时执行的样子。据说最近有多核的单片机,不过成本应该会高很多。对于模拟的多线程,我知道的有两种…...

【LeetCode】剑指 Offer(23)
目录 题目:剑指 Offer 46. 把数字翻译成字符串 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer 46. 把…...

[免费专栏] 汽车威胁狩猎之不应该相信的几个威胁狩猎误区
也许每个人出生的时候都以为这世界都是为他一个人而存在的,当他发现自己错的时候,他便开始长大 少走了弯路,也就错过了风景,无论如何,感谢经历 汽车威胁狩猎专栏长期更新,本篇最新内容请前往: …...

LinuxFTP文件传输服务和DNS域名解析服务
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...

二叉搜索树原理及底层实现
二叉搜索树BST 概念 二叉搜索树又称二叉排序树,它可以是一棵空树,或者是具有以下性质的二叉树:若它的左子树不为空,则左子树上所有节点的值都小于根节点的值;若它的右子树不为空,则右子树上所有节点的值都…...

python自动化办公(一)
本文代码参考其他教程书籍实现。 文章目录文件读写open函数读取文本文件写入文本文件文件和目录操作使用os库使用shutil库文件读写 open函数 open函数有8个参数,常用前4个,除了file参数外,其他参数都有默认值。file指定了要打开的文件名称&a…...
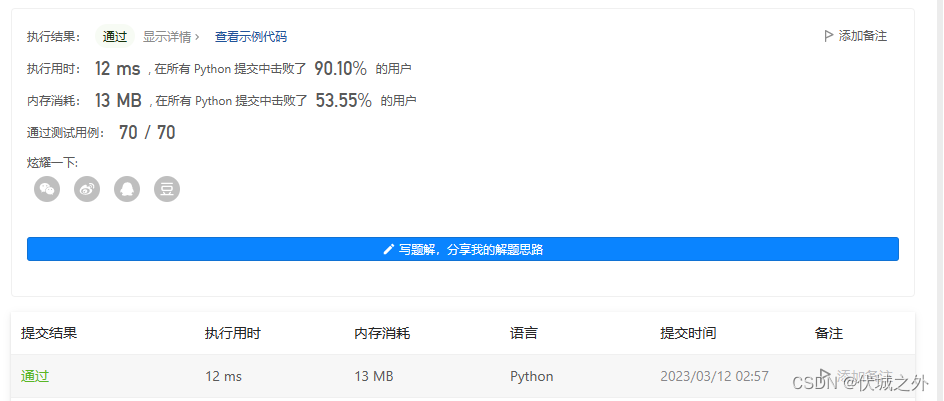
LeetCode - 198 打家劫舍
目录 题目来源 题目描述 示例 提示 题目解析 算法源码 题目来源 198. 打家劫舍 - 力扣(LeetCode) 题目描述 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装…...
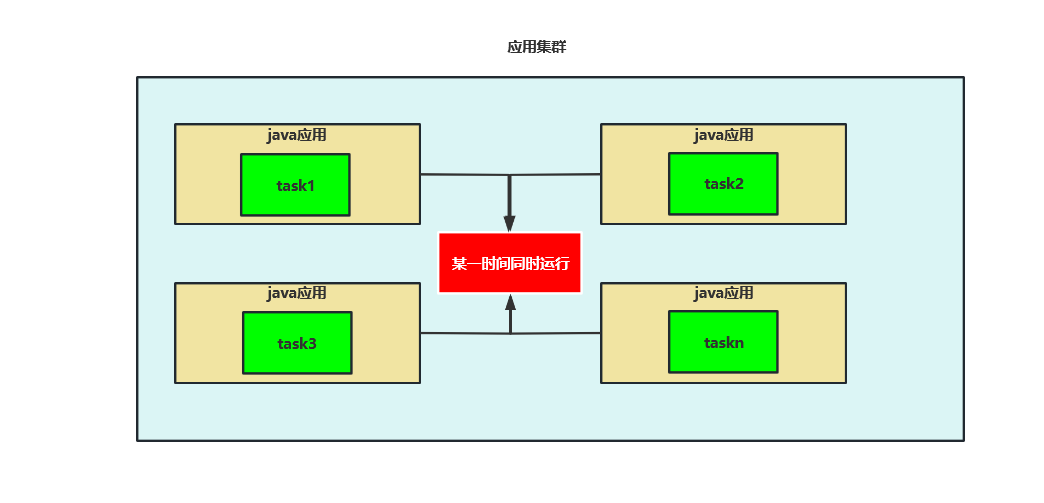
简单粗暴的分布式定时任务解决方案
分布式定时任务1.为什么需要定时任务?2.数据库实现分布式定时任务3.基于redis实现1.为什么需要定时任务? 因为有时候我们需要定时的执行一些操作,比如业务中产生的一些临时文件,临时文件不能立即删除,因为不清楚用户是…...

蓝桥杯第五天刷题
第一题:数的分解题目描述本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。把 2019 分解成 3 个各不相同的正整数之和,并且要求每个正整数都不包含数字 2和 4,一共有多少种不同的分解方法&…...
Java数组的定义和使用(万字详解)
目录 编辑 一. 数组的基本概念 1、什么是数组 2、数组的创建及初始化 1、数组的创建 2、数组的初始化 3、数组的使用 (1)数组中元素访问 (3)遍历数组 二、数组是引用类型 1、初始JVM的内存分布 2、基本类型变量与引用类…...

【SpringBoot】自定义Starter
🚩本文已收录至专栏:Spring家族学习之旅 👍希望您能有所收获 一.概述 在使用SpringBoot进行开发的时候,我们发现使用很多技术都是直接导入对应的starter,然后就实现了springboot整合对应技术,再加上一些简…...
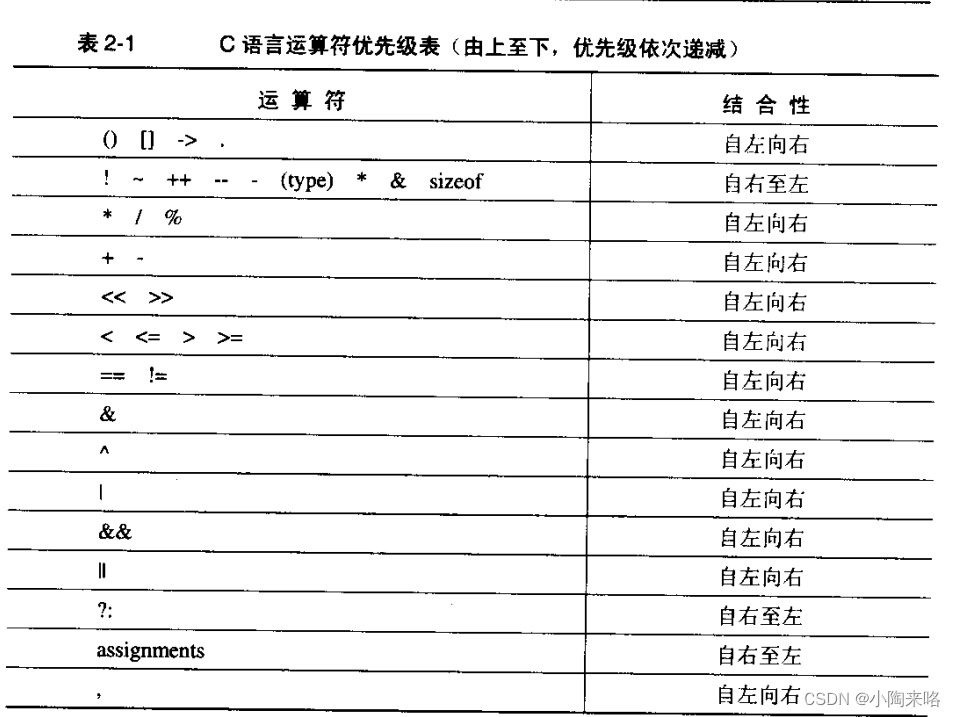
【C陷阱与缺陷】----语法陷阱
💯💯💯 要理解一个C程序,必须理解这些程序是如何组成声明,表达式,语句的。虽然现在对C的语法定义很完善,几乎无懈可击,大门有时这些定义与人们的直觉相悖,或容易引起混淆…...

虹科分享| 关于TrueNAS十问十答
上一篇文章我们向您介绍了虹科新品HK-TrueNAS企业存储,很多小伙伴会疑问到底什么是NAS存储,之前常用的磁盘、磁带属于什么存储架构,NAS存储好在哪里,什么时候使用NAS?今天我们整理了关于TrueNAS的十问十答,…...
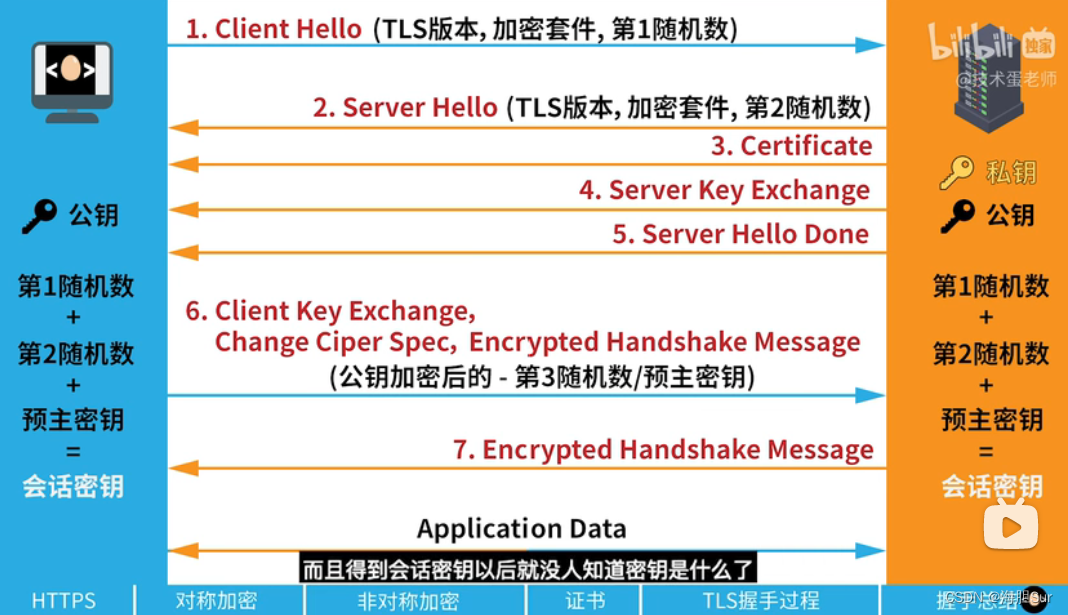
Https 笔记
HTTP TLS TLS 的前身是 SSL 非对称加密的核心: 两个密钥(公私) https 需要第三方CA(证书授权中心)申请SSL证书以确定其真实性 证书种包含了特定的公钥和私钥 密钥交换 自己将私钥上锁后发给对方对方也上锁 在还回来…...

【Python+requests+unittest+excel】实现接口自动化测试框架
一、框架结构: 工程目录 二、Case文件设计 三、基础包 base 3.1 封装get/post请求(runmethon.py) 1 import requests2 import json3 class RunMethod:4 def post_main(self,url,data,headerNone):5 res None6 if heade…...
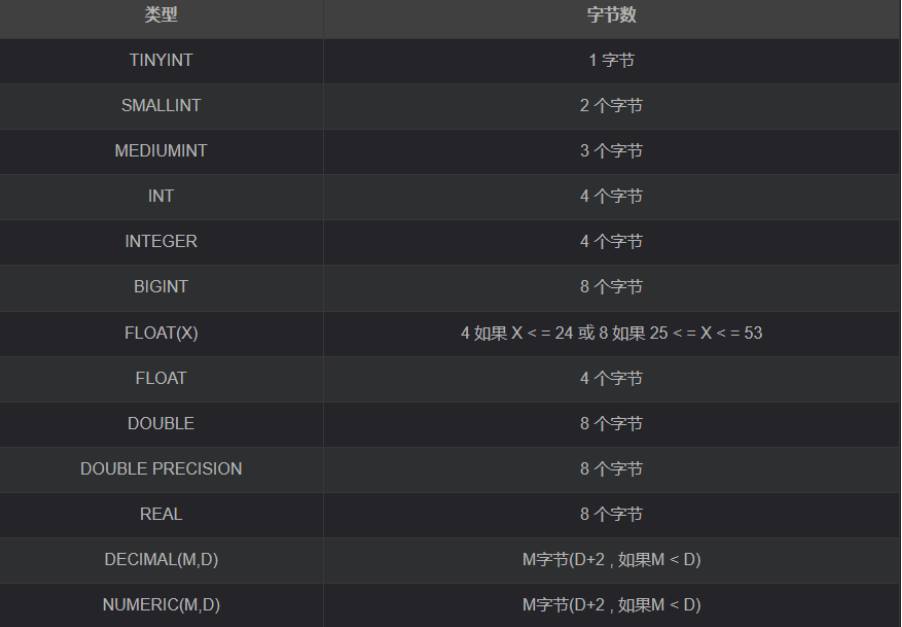
MySQL终端的使用及其数据类型的使用
什么是数据库?数据库(Database)是按照数据结构来组织、存储和管理数据的仓库。每个数据库都有一个或多个不同的 API 用于创建,访问,管理,搜索和复制所保存的数据。我们也可以将数据存储在文件中,…...
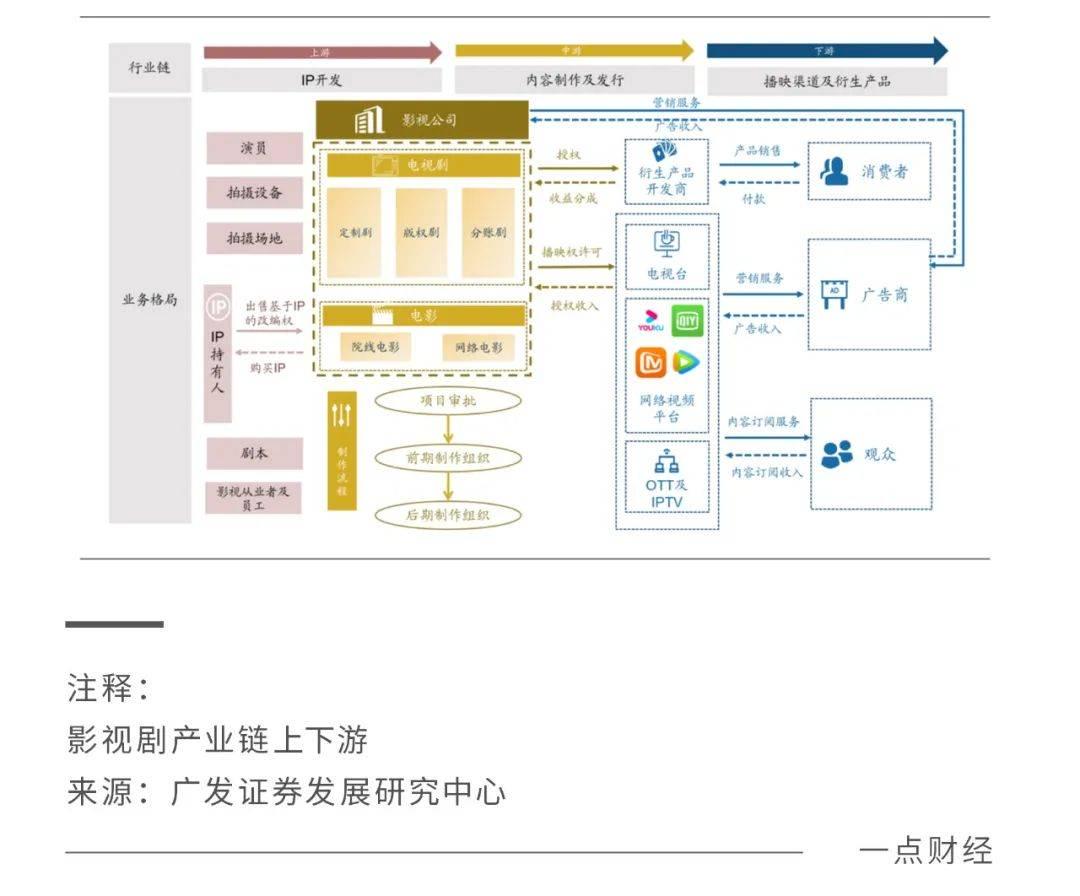
长视频终局:一场考验资金储备的消耗战
赢者通吃,似乎已成为各行各业的常识,但事实真的是这样吗?20世纪70年代,石油价格高涨,在墨西哥湾油田拍卖中高价拍得油田的企业,要么亏损,要么收入低于预期,但仍然有无数企业在高价竞…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
