LeetCode - 198 打家劫舍
目录
题目来源
题目描述
示例
提示
题目解析
算法源码
题目来源
198. 打家劫舍 - 力扣(LeetCode)
题目描述
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例1
输入:[1,2,3,1]
输出:4
解释:
- 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
- 偷窃到的最高金额 = 1 + 3 = 4 。
示例2
输入:[2,7,9,3,1]
输出:12
解释:
- 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
- 偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示
1 <= nums.length <= 1000 <= nums[i] <= 400
题目解析
如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
因此,小偷如果偷了第 i 间,那么必然不能偷第 i + 1间,可以选择偷或不偷第 i + 2间。
上面这种后发状态取决于前面状态的,很容易就想到使用动态规划来求解。
我们定义一个dp数组,dp[i] 的含义是,在 0 ~ i 间屋子中偷盗,小偷所能获得的最大金额。
对于第 i 间屋子,小偷有两种选择:偷、或者不偷,如果:
- 小偷选择偷第 i 间屋子,那么小偷可以获得nums[i]的金额,但是必然不能再偷第 i - 1 间屋子了,而接下来,就变为了偷或不偷第 i - 2间屋子,即有转移方程: dp[i] = dp[i-2] + nums[i]
- 小偷选择不偷第 i 间屋子,那么小偷此时无法获得第 i 间屋子的金额,接下来就变为偷或不偷第 i - 1间屋子,即有转移方程: dp[i] = dp[i-1]
我们只要在上面两个状态中选择最大的即可:
dp[ i ] = max( dp[ i - 1 ], dp[ i - 2 ] + nums[ i ] )
Java算法源码
class Solution {public int rob(int[] nums) {int n = nums.length;int[] dp = new int[n];dp[0] = nums[0];if(n == 1) return dp[0];dp[1] = Math.max(nums[0], nums[1]);if(n == 2) return dp[1];for(int i=2; i<n; i++) {dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i]);}return dp[n-1];}
}
JavaScript算法源码
/*** @param {number[]} nums* @return {number}*/
var rob = function(nums) {const n = nums.lengthconst dp = new Array(n).fill(0)dp[0] = nums[0]if(n == 1) return dp[0]dp[1] = Math.max(nums[0], nums[1])if(n == 2) return dp[1]for(let i=2; i<n; i++) {dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i])}return dp[n-1]
};
Python算法源码
class Solution(object):def rob(self, nums):n = len(nums)dp = [0]*ndp[0] = nums[0]if n == 1:return dp[0]dp[1] = max(nums[0], nums[1])if n == 2:return dp[1]for i in range(2, n):dp[i] = max(dp[i-1], dp[i-2] + nums[i])return dp[n-1]
相关文章:

LeetCode - 198 打家劫舍
目录 题目来源 题目描述 示例 提示 题目解析 算法源码 题目来源 198. 打家劫舍 - 力扣(LeetCode) 题目描述 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装…...
简单粗暴的分布式定时任务解决方案
分布式定时任务1.为什么需要定时任务?2.数据库实现分布式定时任务3.基于redis实现1.为什么需要定时任务? 因为有时候我们需要定时的执行一些操作,比如业务中产生的一些临时文件,临时文件不能立即删除,因为不清楚用户是…...

蓝桥杯第五天刷题
第一题:数的分解题目描述本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。把 2019 分解成 3 个各不相同的正整数之和,并且要求每个正整数都不包含数字 2和 4,一共有多少种不同的分解方法&…...
Java数组的定义和使用(万字详解)
目录 编辑 一. 数组的基本概念 1、什么是数组 2、数组的创建及初始化 1、数组的创建 2、数组的初始化 3、数组的使用 (1)数组中元素访问 (3)遍历数组 二、数组是引用类型 1、初始JVM的内存分布 2、基本类型变量与引用类…...

【SpringBoot】自定义Starter
🚩本文已收录至专栏:Spring家族学习之旅 👍希望您能有所收获 一.概述 在使用SpringBoot进行开发的时候,我们发现使用很多技术都是直接导入对应的starter,然后就实现了springboot整合对应技术,再加上一些简…...
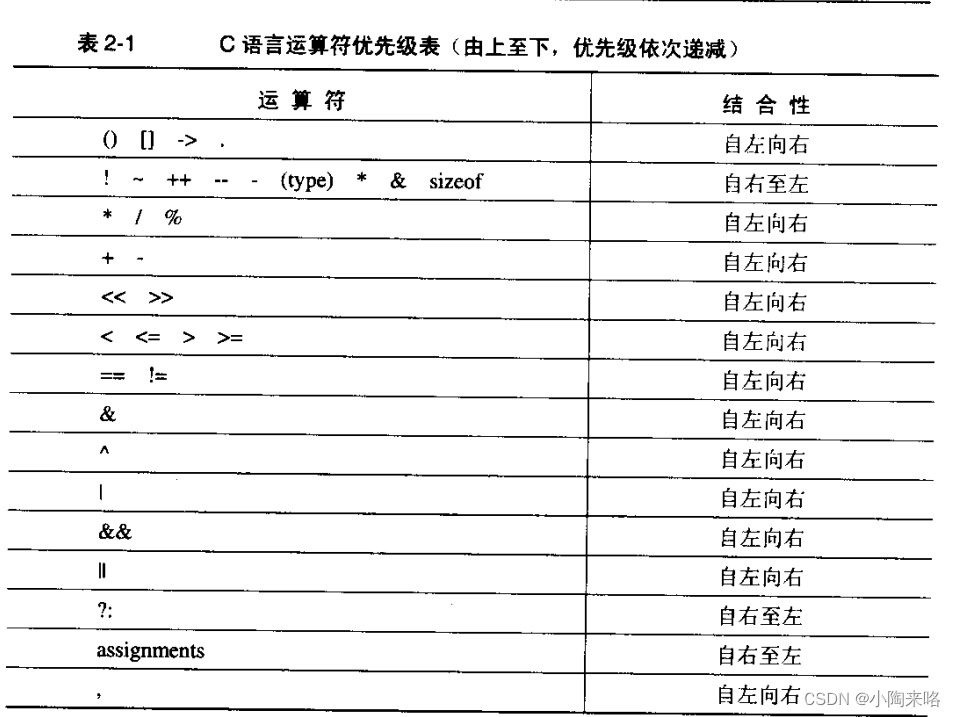
【C陷阱与缺陷】----语法陷阱
💯💯💯 要理解一个C程序,必须理解这些程序是如何组成声明,表达式,语句的。虽然现在对C的语法定义很完善,几乎无懈可击,大门有时这些定义与人们的直觉相悖,或容易引起混淆…...

虹科分享| 关于TrueNAS十问十答
上一篇文章我们向您介绍了虹科新品HK-TrueNAS企业存储,很多小伙伴会疑问到底什么是NAS存储,之前常用的磁盘、磁带属于什么存储架构,NAS存储好在哪里,什么时候使用NAS?今天我们整理了关于TrueNAS的十问十答,…...
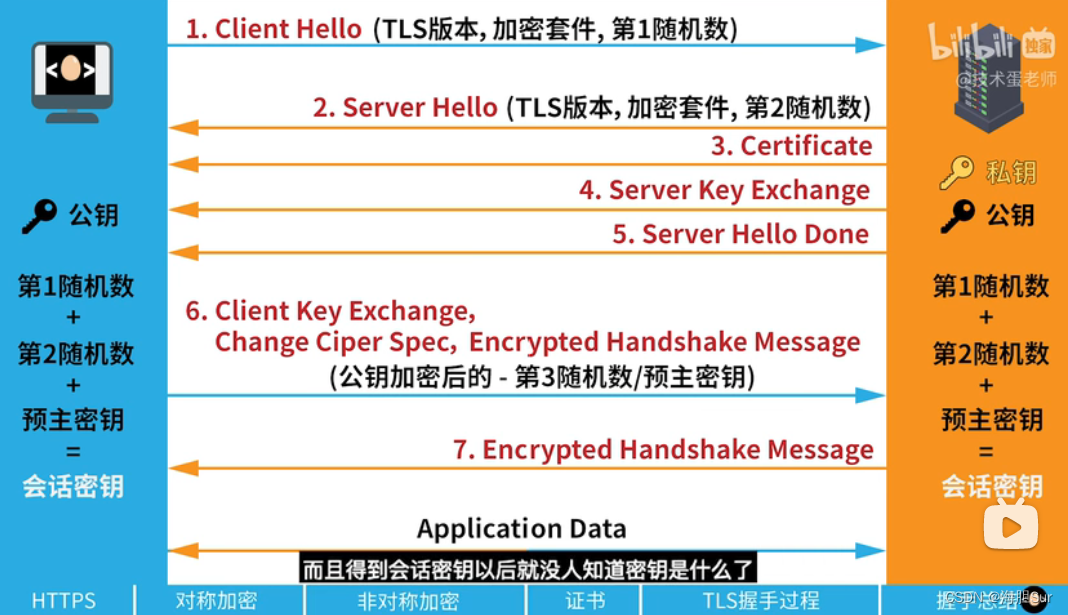
Https 笔记
HTTP TLS TLS 的前身是 SSL 非对称加密的核心: 两个密钥(公私) https 需要第三方CA(证书授权中心)申请SSL证书以确定其真实性 证书种包含了特定的公钥和私钥 密钥交换 自己将私钥上锁后发给对方对方也上锁 在还回来…...

【Python+requests+unittest+excel】实现接口自动化测试框架
一、框架结构: 工程目录 二、Case文件设计 三、基础包 base 3.1 封装get/post请求(runmethon.py) 1 import requests2 import json3 class RunMethod:4 def post_main(self,url,data,headerNone):5 res None6 if heade…...
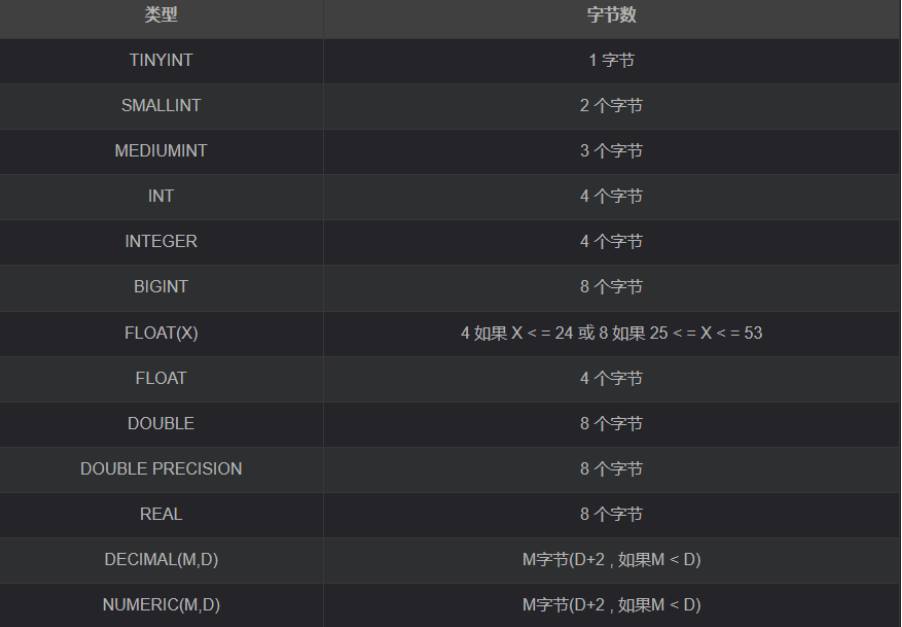
MySQL终端的使用及其数据类型的使用
什么是数据库?数据库(Database)是按照数据结构来组织、存储和管理数据的仓库。每个数据库都有一个或多个不同的 API 用于创建,访问,管理,搜索和复制所保存的数据。我们也可以将数据存储在文件中,…...
长视频终局:一场考验资金储备的消耗战
赢者通吃,似乎已成为各行各业的常识,但事实真的是这样吗?20世纪70年代,石油价格高涨,在墨西哥湾油田拍卖中高价拍得油田的企业,要么亏损,要么收入低于预期,但仍然有无数企业在高价竞…...

javaEE初阶 — CSS 常用的属性
文章目录CSS 常用的属性1 字体属性1.1 设置字体家族 font-family1.2 设置字体大小 font-size1.3 设置字体粗细 font-weight1.4 文字倾斜 font-style2 文本属性2.1 文本颜色2.2 文本对齐2.3 文本装饰2.4 文本缩进2.5 行高3 背景属性3.1 背景颜色3.2 背景图片3.3 背景位置3.4 背景…...

【面试题】如何取消 script 标签发出的请求
大厂面试题分享 面试题库前后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库问题之前在业务上有这样一个场景,通过 script 标签动态引入了一个外部资源,具体方式是这样的const script document.…...
蓝桥杯嵌入式(G4系列):RTC时钟
前言: 关于RTC时钟的HAL库配置我也是第一次,之前都是用库函数的写法,这里写下这篇博客来记录一下自己的学习过程。 STM32Cubemx配置: 首先点击左侧的Timers的RTC,勾选以下选项 进入时钟树配置 进入时间设置࿰…...
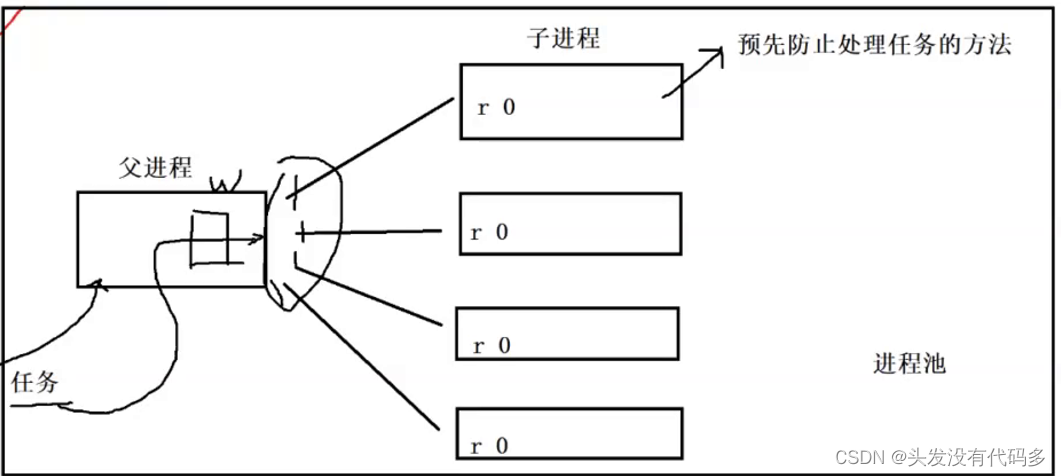
Linux——进程间通信1
目录 进程间通信目的 进程间通信标准 管道 匿名管道 管道实现进程间通信 管道的特点 进程池 ProcessPool.cc Task.hpp 习题 进程间通信目的 数据传输:一个进程需要将它的数据发送给另一个进程 资源共享:多个进程之间共享同样的资源。 通知事件…...

循环语句——“Python”
各位CSDN的uu们你们好呀,今天小雅兰的内容是Python中的循环语句呀,分为while循环和for循环,下面,让我们进入循环语句的世界吧 循环语句 while循环 for循环 continue和break 循环语句小结 人生重开模拟器 设置初始属性 设置性别…...

Python synonyms查找中文任意词汇的同义词近义词
Python synonyms查找中文任意词汇的同义词近义词 作者:虚坏叔叔 博客:https://xuhss.com 早餐店不会开到晚上,想吃的人早就来了!😄 一、安装 对于非专业的开发人员来说可以简单的使用Python一行代码来找到同义词。这…...

三分钟了解http和https
对应测试人员都会听过http请求和响应.在这里给大家介绍http相关的知识 一.http和https基本概念 HTTP:是互联网上应用最为广泛的一种网络协议,是一个客户端和服务器端请求和应答的标准(TCP),用于从WWW服务器传输超文本…...
docker应用:搭建私有云盘
简介:NextCloud是一个开源的云存储解决方案,可以在自己的服务器上搭建个人云存储系统。它提供了与市面上主流云存储服务(如Dropbox、Google Drive)相似的功能,包括文件存储、共享、同步、协作等。NextCloud的主要优势在…...
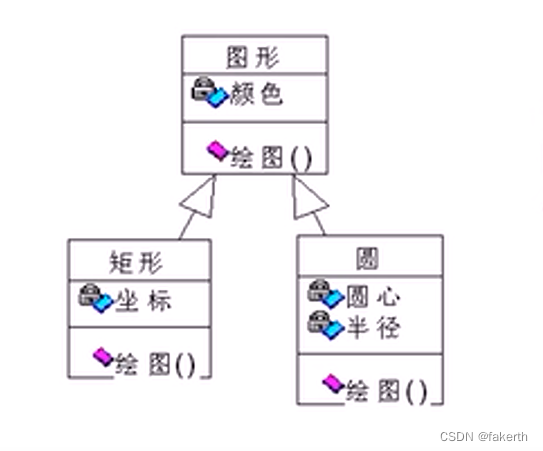
【C++进阶】面向对象
程序 编写程序是为了让计算机解决现实生活中的实际问题。pascal之父、结构化程序设计先驱Niklaus Wirth提出程序 算法 数据结构。程序是完成一定功能的一些列有序指令的集合。指令 操作码 指令。将指令按一定的顺序进行整合,就形成了程序。 机器语言与汇编语言…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...
