联合概率密度函数
目录
- 1. 什么是概率密度
- 由联合概率密度求概率
- 参考链接
1. 什么是概率密度


概率密度到底在表达什么?
外卖在20-40分钟内送达的概率

随机变量落在[20,40]之间的概率。下图中,对总面积做规范化处理,令总面积=1, f ( x ) f(x) f(x)则成为概率密度。

所谓概率密度,是经过了规范化(令总面积为1)之后,所得到的一个函数。经过规范化后,此时,概率密度就成了帮助我们计算概率的工具。
若要计算某变量落在一个区间的概率,就可以直接拿 f ( x ) f(x) f(x)在相应的区间做积分就可以了。因为已经让总面积为1,所以只求阴影部分的面积就可以了。
概率密度的性质

完整的全集概率为1.
由联合概率密度求概率

参考链接
[1] 概率密度到底是个啥?有什么意义?两个引例给你讲明白!
[2] 由联合概率密度求概率;
[3] 抽象的概率密度是怎么来的;
相关文章:

联合概率密度函数
目录 1. 什么是概率密度由联合概率密度求概率参考链接 1. 什么是概率密度 概率密度到底在表达什么? 外卖在20-40分钟内送达的概率 随机变量落在[20,40]之间的概率。下图中,对总面积做规范化处理,令总面积1, f ( x ) f(x) f(x)则成…...

【Java10】成员变量与局部变量
Java中的变量只有两种:成员变量和局部变量。 和C不同,没有全局变量了。 成员变量,field,我习惯称之为**”属性“**(但这些年,因为attribute更适合被叫做属性,所以渐渐不这么叫了)。 …...

Spring Session与分布式会话管理详解
随着微服务架构的普及,分布式系统中的会话管理变得尤为重要。传统的单点会话管理已经不能满足现代应用的需求。本文将深入探讨Spring Session及其在分布式会话管理中的应用。 什么是Spring Session? Spring Session是一个用于管理HttpSession的Spring框…...

从0开始学习pyspark--Spark DataFrame数据的选取与访问[第5节]
在PySpark中,选择和访问数据是处理Spark DataFrame的基本操作。以下是一些常用的方法来选择和访问DataFrame中的数据。 选择列(Selecting Columns): select: 用于选择DataFrame中的特定列。selectExpr: 用于通过SQL表达式选择列。 df.select…...

Fastjson首字母大小写问题
1、问题 使用Fastjson转json之后发现首字母小写。实体类如下: Data public class DataIdentity {private String BYDBSM;private String SNWRSSJSJ;private Integer CJFS 20; } 测试代码如下: public static void main(String[] args) {DataIdentit…...

GuLi商城-商品服务-API-品牌管理-效果优化与快速显示开关
<template><div class"mod-config"><el-form :inline"true" :model"dataForm" keyup.enter.native"getDataList()"><el-form-item><el-input v-model"dataForm.key" placeholder"参数名&qu…...

如何成为C#编程高手?
成为C#编程高手需要时间、实践和持续的学习。以下是一些建议,可以帮助你提升C#编程技能: 深入理解基础知识: 确保你对C#的基本语法、数据类型、控制结构、面向对象编程(OOP)原则有深刻的理解。学习如何使用Visual Stud…...
SpringBoot学习06-[SpringBoot与AOP、SpringBoot自定义starter]
SpringBoot自定义starter SpringBoot与AOPSpringBoot集成Mybatis-整合druid在不使用启动器的情况下,手动写配置类进行整合使用启动器的情况下,进行整合 SpringBoot启动原理源码解析创建SpringApplication初始化SpringApplication总结 启动 SpringBoot自定义Starter定…...

Maven - 在没有网络的情况下强制使用本地jar包
文章目录 问题解决思路解决办法删除 _remote.repositories 文件代码手动操作步骤验证 问题 非互联网环境,无法从中央仓库or镜像里拉取jar包。 服务器上搭建了一套Nexus私服。 Nexus私服故障,无法连接。 工程里新增了一个Jar的依赖, 本地仓…...
JAVA--JSON转换工具类
JSON转换工具类 import com.alibaba.fastjson.JSONObject; import com.fasterxml.jackson.annotation.JsonInclude; import com.fasterxml.jackson.core.JsonProcessingException; import com.fasterxml.jackson.databind.DeserializationFeature; import com.fasterxml.jackso…...

每日复盘-20240705
今日关注: 20240705 六日涨幅最大: ------1--------300391--------- 长药控股 五日涨幅最大: ------1--------300391--------- 长药控股 四日涨幅最大: ------1--------300391--------- 长药控股 三日涨幅最大: ------1--------300391--------- 长药控股 二日涨幅最…...

MySQL 一些用来做比较的函数
目录 IF:根据不同条件返回不同的值 CASE:多条件判断,类似于Switch函数 IFNULL:用于检查一个值是否为NULL,如果是,则用指定值代替 NULLIF:比较两个值,如果相等则返回NULLÿ…...

一个使用率超高的大数据实验室是如何练成的?
厦门大学嘉庚学院“大数据应用实训中心”(以下简称“实训中心”)自2022年建成以来,已经成为支撑“大数据专业”复合型人才培养的重要支撑,目前实训中心在专业课程实验教学、项目实训、数据分析类双创比赛、毕业设计等方面都有深入…...
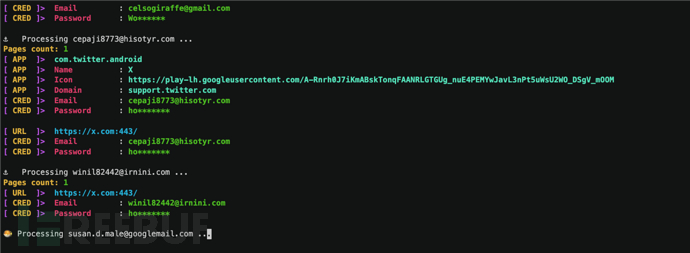
Chiasmodon:一款针对域名安全的公开资源情报OSINT工具
关于Chiasmodon Chiasmodon是一款针对域名安全的公开资源情报OSINT工具,该工具可以帮助广大研究人员从各种来源收集目标域名的相关信息,并根据域名、Google Play应用程序、电子邮件地址、IP地址、组织和URL等信息进行有针对性的数据收集。 该工具可以提…...

如何在Java中实现PDF生成
如何在Java中实现PDF生成 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 在软件开发和企业应用中,生成PDF文档是一项常见的需求。Java作为一种强大…...

Redis 的缓存淘汰策略
Redis 作为一个高性能的内存数据库,提供了多种缓存淘汰策略(也称为过期策略或驱逐策略),用于管理内存使用。当 Redis 达到其内存限制时,系统会根据配置的策略删除一些数据,以释放内存空间。以下是 Redis 支…...

音乐播放器
目录 一、设计目标二、实现流程1. 数据库操作2. 后端功能实现3. 前端UI界面实现4. 程序入口 三、项目收获 一、设计目标 1. 模拟网易云音乐,实现本地音乐盒。 2. 功能分析: 登录功能窗口显示加载本地音乐建立播放列表播放音乐删除播放列表音乐 3.设计思…...

三星组件新的HBM开发团队加速HBM研发
为应对人工智能(AI)市场扩张带来的对高性能存储解决方案需求的增长,三星电子在其设备解决方案(DS)部门内部成立了全新的“HBM开发团队”,旨在提升其在高带宽存储器(HBM)领域的竞争力。根据Business Korea的最新报告,该团队将专注于推进HBM3、…...

图书馆数据仓库
目录 1.数据仓库的数据来源为业务数据库(mysql) 初始化脚本 init_book_result.sql 2.通过sqoop将mysql中的业务数据导入到大数据平台(hive) 导入mysql数据到hive中 3.通过hive进行数据计算和数据分析 形成数据报表 4.再通过sq…...
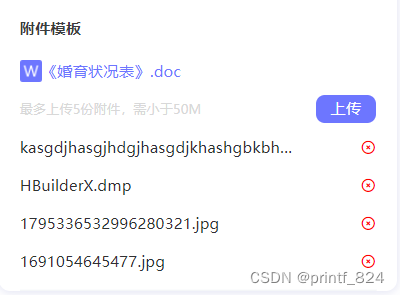
基于uniapp(vue3)H5附件上传组件,可限制文件大小
代码: <template><view class"upload-file"><text>最多上传5份附件,需小于50M</text><view class"" click"selectFile">上传</view></view><view class"list" v…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

02-性能方案设计
需求分析与测试设计 根据具体的性能测试需求,确定测试类型,以及压测的模块(web/mysql/redis/系统整体)前期要与相关人员充分沟通,初步确定压测方案及具体的性能指标QA完成性能测试设计后,需产出测试方案文档发送邮件到项目组&…...
