C++---背包模型---潜水员(每日一道算法2023.3.12)
注意事项:
本题是"动态规划—01背包"和"背包模型—二维费用的背包问题"的扩展题,优化思路不多赘述,dp思路会稍有不同,下面详细讲解。
题目:
潜水员为了潜水要使用特殊的装备。
他有一个带2种气体的气缸:一个为氧气,一个为氮气。
让潜水员下潜的深度需要各种数量的氧和氮。
潜水员有一定数量的气缸。
每个气缸都有重量和气体容量。
潜水员为了完成他的工作需要特定数量的氧和氮。
他完成工作所需气缸的总重的最低限度的是多少?
例如:
潜水员有5个气缸。每行三个数字为:氧,氮的(升)量和气缸的重量:
3 36 12010 25 1295 50 2501 45 1304 20 119
如果潜水员需要5升的氧和60升的氮则总重最小为249(1,2或者4,5号气缸)。
你的任务就是计算潜水员为了完成他的工作需要的气缸的重量的最低值。
输入格式
第一行有2个整数 m,n。它们表示氧,氮各自需要的量。
第二行为整数 k表示气缸的个数。
此后的 k行,每行包括ai,bi,ci,3个整数。这些各自是:第 i个气缸里的氧和氮的容量及气缸重量。
输出格式
仅一行包含一个整数,为潜水员完成工作所需的气缸的重量总和的最低值。
数据范围
1≤m≤21,
1≤n≤79,
1≤k≤1000,
1≤ai≤21,
1≤bi≤79,
1≤ci≤800
输入:输出:#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;const int N = 1010;
int n, m, c; // 需要的氧气,需要的氮气,气缸的数量
int v1[N], v2[N], w[N]; // v1[i]物品i的氧气量,v2[i]物品i的氮气量,重量
int f[N][N];int main() {cin >> n >> m >> c;for (int i = 1; i<=c; i++) cin >> v1[i] >> v2[i] >> w[i]; // 输入每个气缸中包含的氧和氮的数量以及它们各自的重量memset(f, 0x3f3f, sizeof f); // 由于我们要求最小值,所以初始化数组f为无穷大f[0][0] = 0; // 当选取0个氧气和0个氮气的方案就是0//二维费用dp,优化参考01背包for (int i = 1; i<=c; i++) {for (int j = n; j>=0; j--) {for (int k = m; k>=0; k--) {//题目所说的是,当方案的v1不小于n,且v2不小于m时,w的最小值,也就是说可能用到超过n和m的物品,也就会出现负数的情况//这也就是为什么j>=0,k>=0,而不是j>=v1[i],k>=v2[i]//例如f[2][5],也就是需要v1不小于2,v2不小于5,那么如果有一个物品v1是3,v2是4,那么这个物品照样能用只是多出了一些体积但是仍然符合条件//就可以转移为f[0][1] + w, 此时就不需要v1了,因为v1满了,只需要看v2即可(也就是负数也能用,换为0即可)。f[j][k] = min(f[j][k], f[max(0, j - v1[i])][max(0, k - v2[i])] + w[i]);}}}cout << f[n][m];return 0;
}
思路:
经典的y式dp法
1.状态表示
f[i][j][k]:考虑前i个物品,体积不小于j,重量不小于k时的所有方案,属性为Min。
v1[i]第i个物品的氧气,v2[i]第i个物品的氮气,w[i]第i个物品的重量
2.状态计算
以 选择/不选择 第i个物品为划分,
1.当不选择第i个物品时:
f[i][j][k] = f[i-1][j][k]
2.当选择第二个物品时:
f[i][j][k] = min(f[i][j][k], f[i-1][j-v1[i]][k-v2[i]] + w[i])
同时由于我们无法开三维数组,那么就将第i维也就是物品维度优化即可,参考01背包的优化方式。
这里还有一点要提醒:
状态表示分析出的是:考虑前i个物品,体积不小于j,重量不小于k时的所有方案,找w的最小值,也就是说可能用到超过j和k的物品,也就会出现 j-v1[i]或者k-v2[i]负数的情况。
这也就是为什么j>=0,k>=0而不是j>=v1[i],k>=v2[i]。
例如f[2][5],也就是需要物品v1不小于2,v2不小于5,
那么如果有一个物品v1是3,v2是4,那么这个物品照样能用只是多出了一些体积但是仍然符合条件,
就可以转移为f[0][1] + w, 此时就不需要v1了,因为v1满了,只需要看v2即可(负数也能用,换为0即可)。
声明:
算法思路来源为y总,详细请见https://www.acwing.com/
本文仅用作学习记录和交流
相关文章:
)
C++---背包模型---潜水员(每日一道算法2023.3.12)
注意事项: 本题是"动态规划—01背包"和"背包模型—二维费用的背包问题"的扩展题,优化思路不多赘述,dp思路会稍有不同,下面详细讲解。 题目: 潜水员为了潜水要使用特殊的装备。 他有一个带2种气体…...

C++类的成员变量和成员函数详解
类可以看做是一种数据类型,它类似于普通的数据类型,但是又有别于普通的数据类型。类这种数据类型是一个包含成员变量和成员函数的集合。 类的成员变量和普通变量一样,也有数据类型和名称,占用固定长度的内存。但是,在定义类的时候不能对成员变量赋值,因为类只是一种数据类…...
(模拟)(位运算)116. 飞行员兄弟)
(枚举)(模拟)(位运算)116. 飞行员兄弟
目录 题目链接 一些话 切入点 流程 套路 ac代码 题目链接 116. 飞行员兄弟 - AcWing题库 我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦…...
详解Array.prototype.shift.call(arguments)
经常看到如下代码: function foo() {let k Array.prototype.shift.call(arguments);console.log(k) } foo(11,22) //11 Array.prototype.shift.call(arguments)的作用是: 取 arguments 中的第一个参数 一、为啥要这么写,不直接使用argume…...
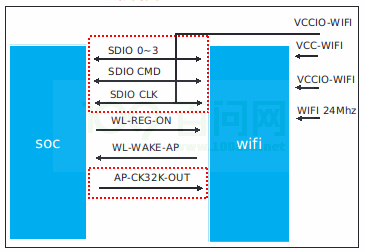
Tina_Linux_Wi-Fi_开发指南
Tina Linux Wi-Fi 开发指南 1 前言 1.1 文档简介 介绍Allwinner 平台上Wi-Fi 驱动移植,介绍Tina Wi-Fi 管理框架,包括Station,Ap 以及Wi-Fi 常见问题。 1.2 目标读者 适用Tina 平台的广大客户和对Tina Wi-Fi 感兴趣的同事。 1.3 适用范…...
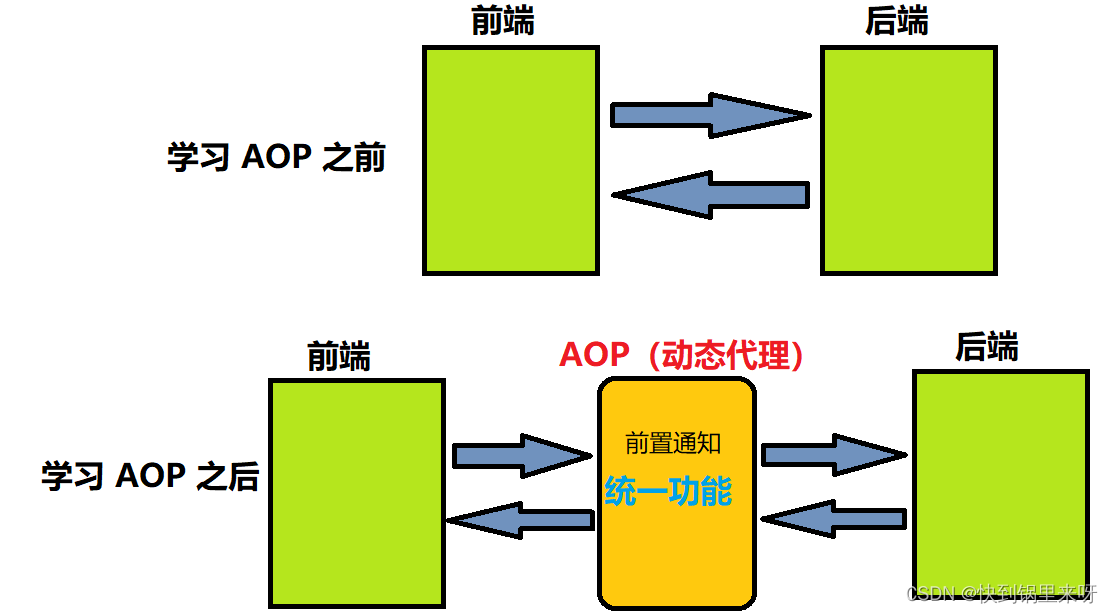
Spring AOP(AOP概念、组成、Spring AOP实现及实现原理)
文章目录1. Spring AOP 是什么2. 为什么要用 AOP3. 怎么学 Spring AOP4. AOP 组成5. Spring AOP 实现5.1 添加 Spring AOP 框架支持5.2 定义切面和切点5.3 实现通知方法5.4 使⽤ AOP 统计 UserController 每个⽅法的执⾏时间 StopWatch5.4 切点表达式说明 AspectJ6. Spring AOP…...
8.条件渲染指令
目录 1 v-if v-show 2 v-if v-else-if v-else 1 v-if v-show v-if与v-show都可以控制DOM的显示与隐藏 由于flag是布尔值,所以这里可以直接写 v-if"flag" 当flag为true的时候,v-if与v-show控制的div都会被显示出来 当flag为false的时候&a…...
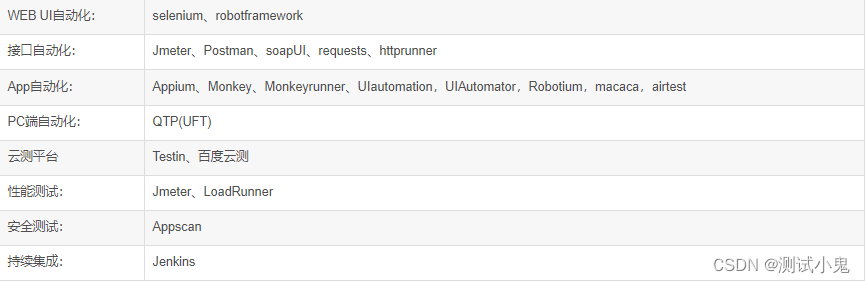
2023年全网最全最细最流行的自动化测试工具有哪些?你都知道吗!
下面就是我个人整理的一些比较常用的自动化测试工具,并且还有视频版本的详细介绍,同时在线学习人数超过1000人! B站讲的最详细的Python接口自动化测试实战教程全集(实战最新版)一:前言 随着测试工程师技能和…...

网络安全——数据链路层安全协议
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.数据链路层安全协议简介 1.数据链路安全性 二.局域网数据链路层协议 1.…...
编译原理基础概念
一、什么是编译程序编译程序是一种程序,能够将某一种高级语言编写的源程序改造成另一种低级语言编写的目标程序,他们在逻辑上等价、完成相同的工作二、编译阶段1、当目标程序是机器语言时,编译阶段:(1)编译…...
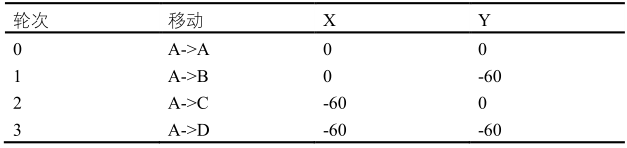
蔬菜视觉分拣机器人的设计与实现(RoboWork参赛方案)
蔬菜视觉分拣机器人的设计与实现 文章目录蔬菜视觉分拣机器人的设计与实现1. 技术栈背景2. 整体设计3. 机械结构3.1 整体结构3.2 底座结构3.3 小臂结构3.4 大臂结构3.5 负载组件结构3.6 末端执行器结构4. 硬件部分4.1 视觉系统4.1.1 光源4.1.2 海康工业相机4.2 传送带系统4.2.1…...
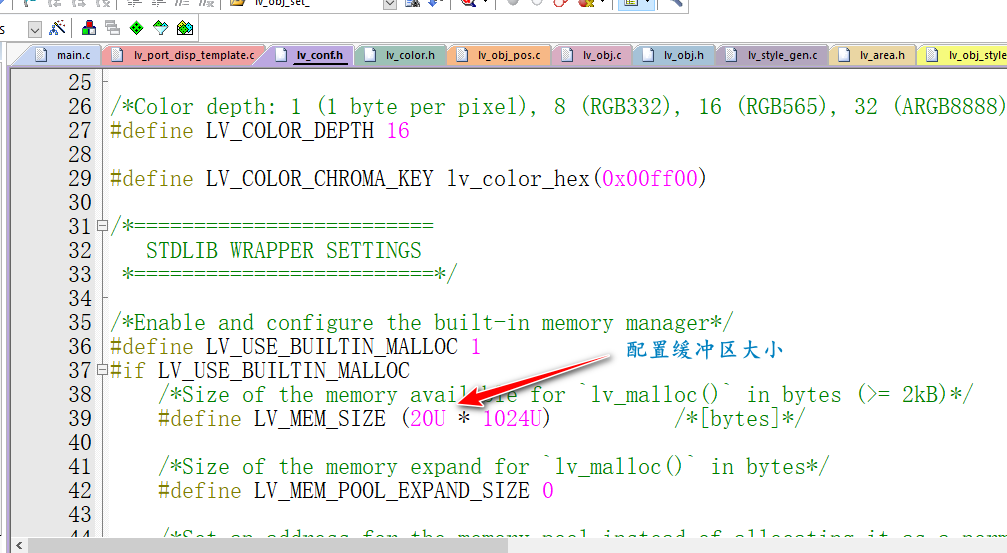
【LVGL移植】STM32F1基于STM32CubeMX配置硬件SPI驱动1.8寸TFT ST7735S跑LVGL图形demo
【LVGL移植】STM32F1基于STM32CubeMX配置硬件SPI驱动1.8寸TFT ST7735S屏幕跑LVGL图形demo🎬运行LVGL 按键组件demo ✨基于STM32CubeMX配置工程是因为方便移植,只要是STM32芯片,拿到我的这个工程源码就可以根据自己的stm32芯片,自…...
写给20、21级学生的话
写给20、21级学生的话前言一、关于招聘变招生,你怎么看?二、对于即将实习/已经实习的学生,你有什么建议?1.学习方面2.提升方面三、思想成年真的很重要前言 最近,有一些同学遇到的实习问题,我统一回复下&…...
功能测试用例多次录制后,我丢掉了selenium,选择龙测AI-TestOps云平台
目录一、如何使用龙测AI-TestOps云平台1、进入龙测AI-TestOps云平台2、新建项目3、新建流程图4、创建任务5、查看任务状态6、查看报告、图片7、下载流程图、测试报告、excel用例二、龙测AI-TestOps云平台AI功能介绍1、NLP2、视频AI转流程图三、总结功能测试用例多次录制后&…...

【C++知识点】C++20 常用新特性总结
✍个人博客:https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 📚专栏地址:C/C知识点 📣专栏定位:整理一下 C 相关的知识点,供大家学习参考~ ❤️如果有收获的话,欢迎点赞👍…...

数据库体系结构概念--集中式数据库、分布式数据库
数据库模式 前言: 平时我们接触的‘数据库’一般指的是DBMS,数据库管理系统,DBMS是软件如:mysql、oracle、dm等等都是集中式数据库,但它们不能代表整个数据库,只是通过这些软件来管理相应的数据内容&#…...
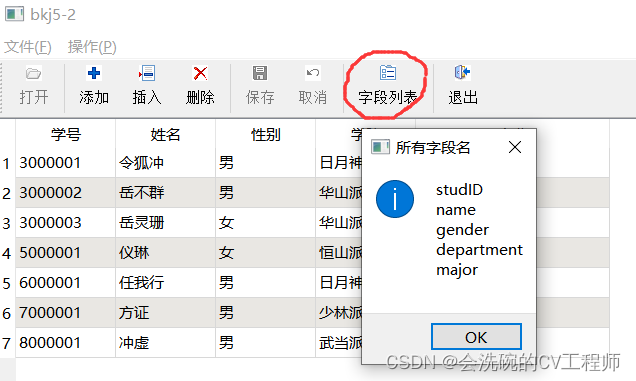
PyQt5数据库开发2 5.2 QSqlRelationalTableModel
目录 一、Qt窗体设计 1. 新建Qt项目 2. 添加组件 3. 添加资源 4. 添加Action 5. 添加工具栏 6. 添加菜单项 7. 添加退出功能 二、SQL Server下建表插数据 1. 建立表 2. 插入数据 3. 单表数据 4. 联合查询 三、代码实现 1. 新建项目目录 2. 编译窗体文件和资…...

树莓派——智能家居第一步
辛辛苦苦配了成功让树莓派开始工作了,开始搞智能家居!大体思路:基于工厂模式,分模块来实现上图分为三部分:主控、外设、控制主控我采用的是树莓派的4b4G版本,外设包括四个区域的灯(我的和上图有…...
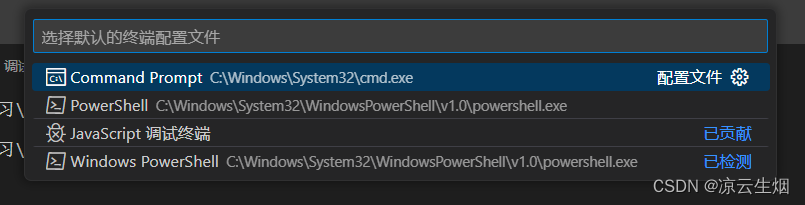
【Golang】Golang基础入门级教程 -- 0基础安装搭建Go语言开发环境
目录 安装和下载GO语言 下载 下载地址 版本的选择 安装 Windows安装 Linux下安装 Mac下安装 检查 GOROOT和GOPATH GOPROXY Go开发编辑器 VS Code介绍 下载与安装 配置 Go扩展 第一个Go程序 Hello World go mod init 编写 编译 VSCode切换默认终端 本篇文章…...
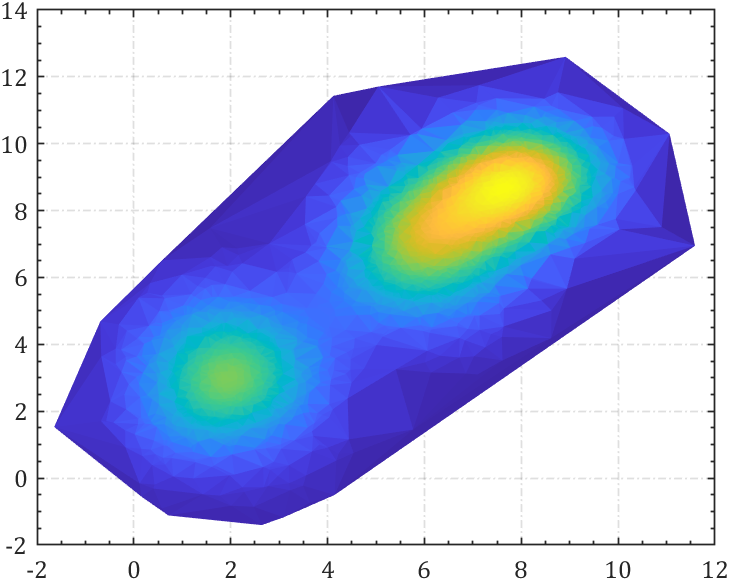
MATLAB | 如何解决实验数据散点图重叠问题(overlap)
本期部分实验效果: 这期讲一下如果数据重合严重该咋办(overlap),事先说明,本文中的绘图均使用一个几行的简单小代码进行了修饰: function defualtAxes axgca;hold on;box on ax.XGridon; ax.YGridon; ax.XMinorTickon; ax.YMinor…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
