算法基础-----【动态规划】

动态规划(待完善)

动规五部曲分别为：

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式（状态转移公式）
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组、

动态规划的核心就是递归+剪枝（存储键值，下次不再访问，用空间换时间）

找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！
这道题目我举例推导状态转移公式了么？
我打印dp数组的日志了么？
打印出来了dp数组和我想的一样么？
或者更清晰的知道自己究竟是哪一点不明白，是状态转移不明白，还是实现代码不知道该怎么写，还是不理解遍历dp数组的顺序。

动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的，例如：有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

动态规划中dp[j]是由dp[j-weight[i]]推导出来的，然后取max(dp[j], dp[j - weight[i]] + value[i])。

但如果是贪心呢，每次拿物品选一个最大的或者最小的就完事了，和上一个状态没有关系。

所以贪心解决不了动态规划的问题。

​ 动态规划的解题步骤：（1）确定dp数组以及下标含义 （2）确定递推公式 （3）dp数组如何初始化 （4）确定遍历顺序 （5）例举推导dp数组。

【基础题目】

【509】斐波那契数列

解题步骤：

1）确定dp数组以及下标含义

dp[i]: 第i个数的斐波那契数值是dp[i]。

2）确定递推公式

dp[i] = dp[i-1]+dp[i-2]

3）dp数组如何初始化

dp[0] = 0 dp[1] = 1

4）确定遍历顺序

从前向后遍历

5）例举推导dp数组。

按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2]，我们来推导一下，当N为10的时候，dp数组应该是如下的数列：

0 1 1 2 3 5 8 13 21 34 55

如果代码写出来，发现结果不对，就把dp数组打印出来看看和我们推导的数列是不是一致的。

//动态规划基础问题
/*递归的方法 ：时间复杂度o(n^2) 空间复杂度o(1)*/
class Solution {
public:int fib(int n) {if(n<2)return n;return fib(n-1)+fib(n-2);}
};
/*动态规划的方法 时间复杂度o(n) 空间复杂度o(n)(经典做法)*/
class Solution {
public:int fib(int n) {if(n<2)return n;vector<int> dp(n+1);dp[0] = 0;dp[1] = 1;for(int i = 2;i<n+1;i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
};/*动态规划简写 时间复杂度o(n) 空间复杂度o(1)*/
class Solution {
public:int fib(int n) {if(n<2)return n;vector<int> dp(2);dp[0] = 0;dp[1] = 1;for(int i = 2;i<n+1;i++){int sum = dp[0]+dp[1];dp[0] = dp[1]; dp[1] = sum;}return dp[1];}
};

【70】爬楼梯

确定递归数列：找规律 f(n) = f(n-1)+f(n-2)
确定终值f(1) = 1 f(0) = 0
存储节点：定义数组存储节点
最标准的做法，要是还要优化空间复杂度就考虑上面的做法

class Solution {
public:int climbStairs(int n) {if(n<2)return n;//(f(1)= 1,f(2) =2)vector<int> f(n+1);f[1] =1;f[2] =2;for(int i =3;i<n+1;i++){f[i] =f[i-1]+f[i-2];}return f[n];}
};

【118】杨辉三角

注意申请数组具体那一行
注意改变数组的长度的函数resize(为了防止0出现)

class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> ret(numRows);for (int i = 0; i < numRows; ++i) {ret[i].resize(i + 1);ret[i][0] = ret[i][i] = 1;for (int j = 1; j < i; ++j) {ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];}}return ret;}
};

【背包问题】

【0-1背包】

对于面试，掌握01背包和完全背包，多重背包。

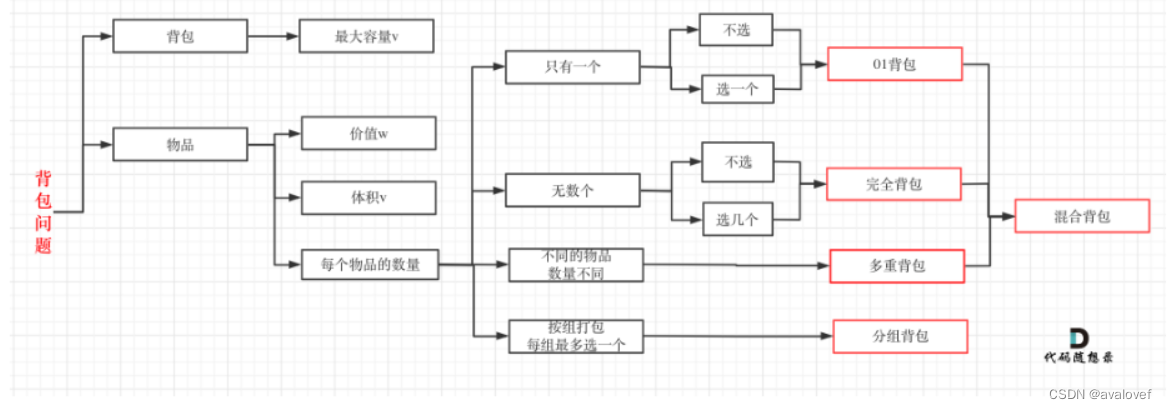
基础引用：对于0，1背包，就是m个物品，给定对应的重量和价值，最大容量为n，这些物品你只能选一个或者不选（01），求最大价值。

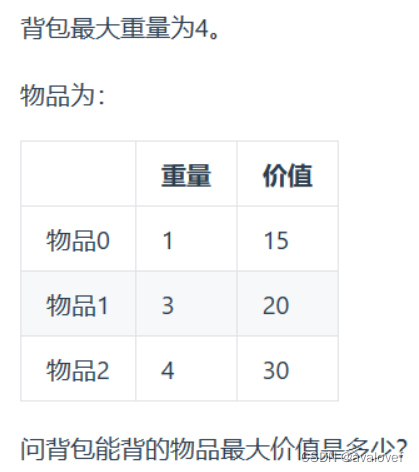
动态规划五部曲：

（1）确定dp数组以及下标的含义dp[i] [j ]:表示下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

（2）确定递推公式：

• 放物品i：由dp[i - 1] [j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i] [j]就是dp[i - 1] [j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)
• 放物品i：由dp[i - 1] [j - weight[i]]推出，dp[i - 1] [j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1] [j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

所以递归公式： dp[i] [j] = max(dp[i - 1] [j], dp[i - 1] [j - weight[i]] + value[i]);

（3）初始化dp数组

​ 后面的公式是根据前面来推导的，所以初始化正确了才能导致dp数组正确

​ 状态转移方程 dp[i] [j] = max(dp[i - 1] [j], dp[i - 1] [j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

​ 要求出 dp[ 0 ] [ j]:也就是求种类0在不同重量下的最大价值：当j<weight[0]的时候肯定装不下，都为0.所以j从weight[0]开始初始化，都为value[0]:

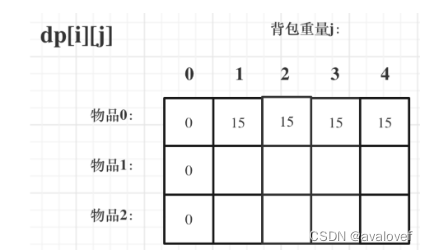
(4)确定遍历顺序：先遍历物品，再遍历重量：

for(int i =1;i<m;i++){for(int j = 0;j<=m;j++){if(j<weight[i]){dp[i][j] = dp[i-1][j];//不放}else{dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);//放}}
}

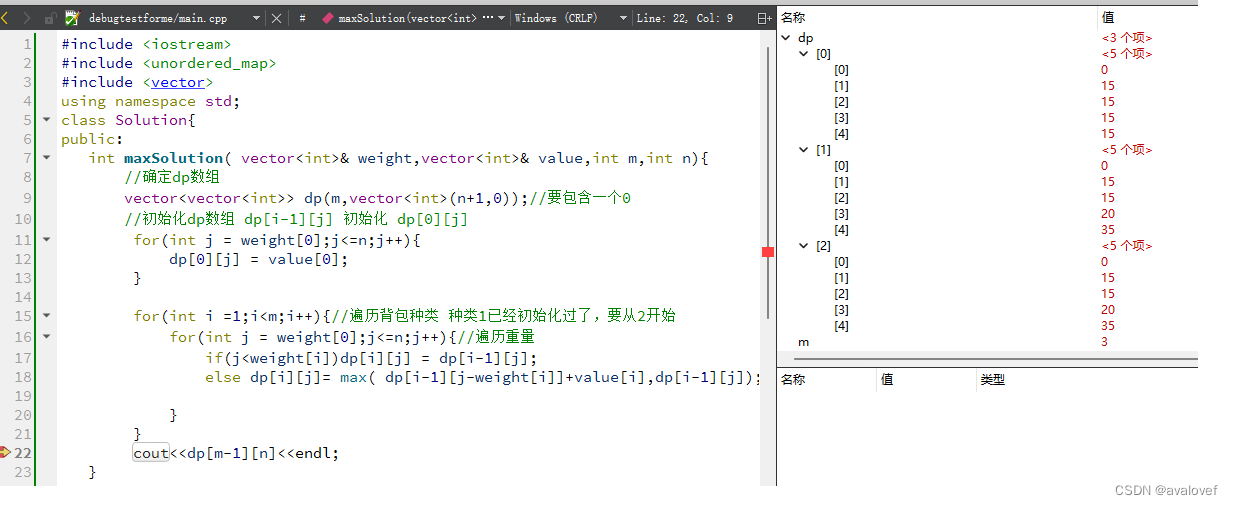
（5）举例推导dp数组

#include <iostream>
#include <unordered_map>
#include <vector>
using namespace std;
class Solution{
public:int maxSolution( vector<int>& weight,vector<int>& value,int m,int n){//确定dp数组vector<vector<int>> dp(m,vector<int>(n+1,0));//要包含一个0//初始化dp数组 dp[i-1][j] 初始化 dp[0][j]for(int j = weight[0];j<=n;j++){dp[0][j] = value[0];}for(int i =1;i<m;i++){//遍历背包种类 种类1已经初始化过了，要从2开始for(int j = weight[0];j<=n;j++){//遍历重量if(j<weight[i])dp[i][j] = dp[i-1][j];else dp[i][j]= max( dp[i-1][j-weight[i]]+value[i],dp[i-1][j]);}}cout<<dp[m-1][n]<<endl;}};int main()
{int m;//背包种类int n;//空间容量 bagweightvector<int> weight(m,0);vector<int> value(m,0);
//    cin >>m>>n;
//    for(int i =0;i<m;i++){
//        cin>> cap[i];
//    }
//    for(int i =0;i<m;i++){
//        cin>> value[i];
//    }m = 3;//背包种类n = 4;//最大容量是4weight = {1,3,4};//重量value = {15,20,20};//价值Solution s;int res = s.maxSolution(weight,value,m,n);return 0;
}

【416】分割等和子集

​ 0-1背包是可以用回溯的方式去做的，和【698】【473】都有相同的做法。

​ 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

j:容量，dp[j]最大价值，可以看到都是倒叙取最大值，最后的dp数组是：

0	1	2	3	4	5	6	7	8	9	10	11
0	1	1	1	1	5	6	6	6	6	10	11

class Solution {
public:bool canPartition(vector<int>& nums) {int sum =0;for(auto num:nums){sum+=num;}if(sum%2 == 1)return false;//要是不能平分直接退出int n = sum/2;vector<int> dp(n+1,0);//初始化dp数组//dp遍历for(int i =0;i<nums.size();i++){for(int j=n;j>=nums[i];j--){//特别注意这个nums[i]dp[j] = max(dp[j],dp[j-nums[i]]+nums[i]);cout<<"i:"<<i<<" dp["<<j<<"]:"<<dp[j]<<endl;}}//判断if(dp[n] == n)return true;return false;}
};

【1049】最后一块石头的重量

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int n = stones.size();int sum =0;for(auto item:stones){sum+=item;}int target = sum/2;vector<int> dp(target+1,0);for(int i =0;i<n;i++){for(int j = target;j>=stones[i];j--){dp[j] = max(dp[j],dp[j-stones[i]]+stones[i]);}}return sum-2*dp[target];//注意最后返回的数值}
};

【494】目标和

【17】一和零

【32】最长有效括号

给你一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长有效（格式正确且连续）括号子串的长度。
看到最长就可以开始考虑用动规了：
解：
(1)确定dp数组和其下标
dp[i] :到[0,i]的最长有效子串长度（一维就够了，不依赖后面的字符，不需要移动）
(2)确定状态转移方程

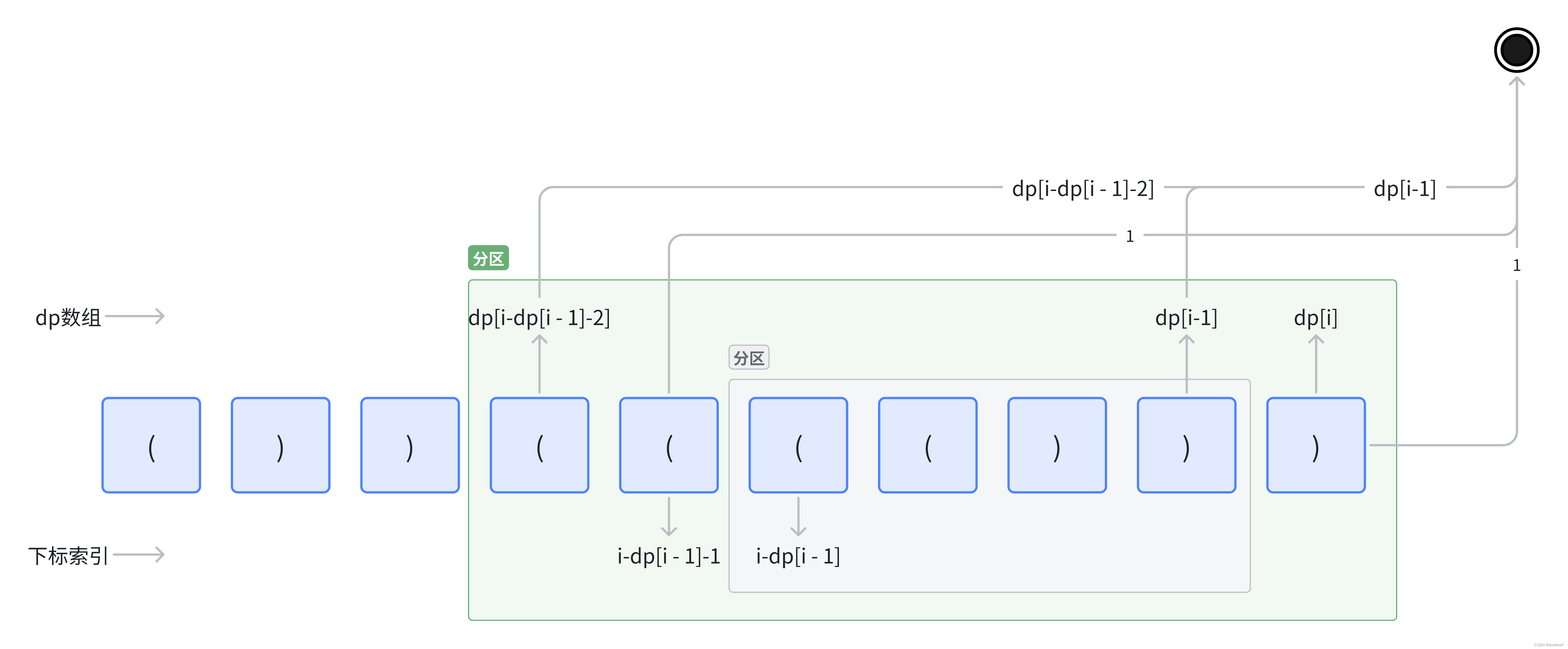
if(s[i] == ')'){if(s[i-1] =='('){dp[i] = dp[i-1]+2;} else{dp[i] = dp[i-1];}
}else{//没有子串计数dp[i] = dp[i-1];
}

【完全背包】

完全背包内层循环从头开始

【322】零钱兑换

class Solution {
public:int coinChange(vector<int>& coins, int amount) {//初始化dp数组vector<int> dp(amount+1,INT_MAX);dp[0] = 0;for(int i =0;i<coins.size();i++){for(int j = coins[i];j<=amount;j++){//遍历背包 注意初始化的位置if(dp[j-coins[i]] !=INT_MAX){// 如果dp[j - coins[i]]是初始值则跳过dp[j] = min(dp[j],dp[j-coins[i]]+1);}}}if(dp[amount] == INT_MAX) return -1;return dp[amount];}
};

遍历的过程：

以coins = [1,2,5]，amount = 11为例子：

	0	1	2	3	4	5	6	7	8	9	10	11
初始化	0	M	M	M	M	M	M	M	M	M	M	M
1(只有1)	0	1	2	3	4	5	6	7	8	9	10	11
2（1或2）	0	1	1	2	2	3	3	4	4	5	5	6
5（1或2或5）	0	1	1	2	2	1	2	2	3	3	2	3

【139】单词拆分

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {//存储wordDict 背包unordered_set<string> wordMap(wordDict.begin(),wordDict.end());vector<int> dp(s.size()+1,false);//dp数组dp[0]= true;//求的是排列数，有顺序，背包在外层for(int i =1;i<=s.size();i++){//遍历背包for(int j =0;j<i;j++){//遍历物品string tmp = s.substr(j,i-j);if(wordMap.find(tmp)!= wordMap.end()&&dp[j] == true){dp[i] = true;}}}return dp[s.size()];}
};

【打家劫舍】

【198】打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

按照五部曲进行推导

class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();//确定dp数组 dp[i]存放最高金额vector<int> dp(n);if(n == 0)return 0;if(n == 1)return nums[0];if( n == 2)return max(nums[0],nums[1]);dp[0] = nums[0];dp[1] = max(nums[0],nums[1]);for(int i = 2;i<n;i++){dp[i] = max(dp[i-1],nums[i]+dp[i-2]);cout<<dp[i]<<endl;}return dp[n-1];}
};

【213】

【337】

【子序列问题】

子序列包括连续、不连续、编辑距离、回文等等…

【300】最长子序列

（1)根据返回值确定dp[i]:以nums[i]结尾的最长子序列的数组长度。

（2)状态转移方程： if(nums[i]>nums[j])dp[i] = max(dp[i],dp[j]+1);（往前对比）

（3）dp数组初始化，dp[i] = 1

(4) 确定遍历顺序，dp[i+1] = dp[i]

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int res =1;if(nums.size() == 1)return 1;if(nums.size() == 0)return 0;vector<int> dp(nums.size(),1);for(int i =1;i<nums.size();i++){for(int j = 0;j<i;j++){if(nums[i]>nums[j])dp[i] = max(dp[i],dp[j]+1);}if(dp[i]>res)res = dp[i];//不一定是最后一个元素，取最长子序列}return res;}
};

【301】

【152】乘积最大子数组

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。测试用例的答案是一个 32-位 整数。

注意：这道题需要维护当前最小值，存在负数让最大值变成最小值的情况。
1.确定dp数组和下标
本来是只想取dp[i]:以下标 i 结尾的连续子序列的乘积的最大值。
即可得：dp[i] = max(dp[i - 1] * nums[i], nums[i])，但是如果nums[i]是负数的话，会把最大值变化最小值。或者前面累乘的最小值会变成最大值。所以我们还要加一维去维护当前最小值：
dp[i][0]:下标为i范围内的子数组最大乘积。
dp[i][1]:下标为i范围内的子数组最小乘积。
2.确定递推公式

	if nums[i] >0dp[i][0] = max(dp[i - 1][0] * nums[i], nums[i]);dp[i][1] = min(dp[i - 1][1]* nums[i], nums[i]);else dp[i][0] = max(dp[i - 1][1] * nums[i], nums[i]);dp[i][1] = min(dp[i-1][0]*nums[i],nums[i]);

3.确定初始化dp
dp[0][1] = nums[0]
dp[0][0] = nums[0]
4.初始化顺序
从左到右,从上到下
5.例举dp数组
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

2	2
6	3
-2	-12
4	-48
得到第一列最大值以后，还要去选择其中最大的值进行输出：

class Solution {
public:int maxProduct(vector<int>& nums) {vector<vector<int>> dp(nums.size(),vector<int>(2,0));int m = nums.size();dp[0][0] = nums[0];dp[0][1]= nums[0];for(int i = 1;i<m;i++){if(nums[i]>0){dp[i][0] = max(dp[i-1][0]*nums[i],nums[i]);dp[i][1] = min(dp[i-1][1]*nums[i],nums[i]); }else{dp[i][0] = max(dp[i-1][1]*nums[i],nums[i]);dp[i][1] = min(dp[i-1][0]*nums[i],nums[i]); }}int res =dp[0][0];for(int i =0;i<m;i++){res = max(dp[i][0],res);}return res;}
};

为了防止越界，可以这样做：用例[0,10,10,10,10,10,10,10,10,10,-10,10,10,10,10,10,10,10,10,10,0]

class Solution {
public:int maxProduct(vector<int>& nums) {int len = nums.size();vector<long long> dpMax(len);vector<long long> dpMin(len);dpMax[0] = nums[0];dpMin[0] = nums[0];long long maxProduct = dpMax[0];for (int i = 1; i < len; ++i) {long long tmp1 = nums[i] * dpMin[i - 1];long long tmp2 = nums[i] * dpMax[i - 1];if (tmp1 < INT_MIN) {tmp1 = INT_MIN;//钳住}if (tmp2 < INT_MIN) {tmp2 = INT_MIN;}dpMax[i] = max(static_cast<long long>(nums[i]), max(tmp1, tmp2));dpMin[i] = min(static_cast<long long>(nums[i]), min(tmp1, tmp2));maxProduct = max(maxProduct, dpMax[i]);}return static_cast<int>(maxProduct);}
};

【718】最长重复子数组

多维动态规划

与图论的区别就是多维动态规划还是需要转移方程的。图论一般就是DFS和BFS直接做。
动态规划最开始做的时候，为了便于理解，都用二维dp数组（方便理解）

【62】不同路径

题目：一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？
解法1：利用深搜(类似于深搜)，由于只有两个方向，可以枚举出来有多少种路径。注意题目中说机器人每次只能向下或者向右移动一步，那么其实机器人走过的路径可以抽象为一棵二叉树，而叶子节点就是终点！

class Solution {
public:int dfs(int i,int j,int m,int n){if(i>=m || j>=n)return 0;//边界条件if(i == m-1 && j ==n-1)return 1;//找到了一条路return dfs(i+1,j,m,n) + dfs(i,j+1,m,n);//返回结果，左边+右边}int uniquePaths(int m, int n) {return dfs(0,0,m,n);//从(0,0)开始}
};

假设是3*3列网格，递归路径是：

                    (0, 0)/      \(1, 0)      (0, 1)/    \      /     \(2, 0)  (1, 1) (1, 1) (0, 2)/  \   /  \   /  \   /  \超出边界  (2, 1) (2, 1) (1, 2) (1, 2)/  \   /  \   /  \   /  \超出边界 (2, 2) (2, 2) 超出边界 (2, 2)/      /     \        \终点    终点   终点     终点

但是这种方法会超时，因为这个树的深度是m+n-1,这棵树的深度其实就是m+n-1（深度按从1开始计算）。那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树（其实没有遍历整个满二叉树，只是近似而已。
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1)，可以看出，这是指数级别的时间复杂度，是非常大的。

解法2：动态规划
（1）确定dp数组以及下标的含义
dp[i][j] :[0][0]到坐标[i][j]共有dp[i][j] 条不同的路径。
（2）确定dp状态转移公式
想想dp[i][j]上一个状态是什么，分别是dp[i-1][j]和dp[i][j-1]
dp[i-1][j]表示[0][0]到坐标[i][j]共有dp[i-1][j]条不同的路径，dp[i][j-1]表示[0][0]到坐标[i][j-1]共有dp[i][j-1]条不同的路径
所以可以明确dp[i][j] = dp[i-1][j]+dp[i][j-1]
（3）dp数组如何初始化
dp[i][0] = 1,从[0][0]到[i][0]的路径只有1条
dp[0][j] = 1,从[0][0]到[0][j]的路径只有1条

for(int i =0;i<m;i++)dp[i][0]=1;
for(int j =0;j<n;j++)dp[0][j]=1;

（4）确定遍历顺序
dp[i][j] = dp[i-1][j]+dp[i][j-1],从左到右，从上到下遍历，保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
（5）举例推导dp数组：按照3*3的表格为例子，则最后一个dp[m-1][n-1]就是最后返回的6条不同路径。

坐标	0	1	2
0	1	1	1
1	1	2	3
2	1	3	6

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m,vector<int>(n,0));//进行初始化for(int i =0;i<m;i++)dp[i][0] = 1;for(int j =0;j<n;j++)dp[0][j] = 1;//确定遍历顺序，从左到右从上到下for(int i =1;i<m;i++){for(int j=1;j<n;j++){dp[i][j] = dp[i-1][j]+dp[i][j-1];}}return dp[m-1][n-1];}
};

• 时间复杂度：O(m × n)
• 空间复杂度：O(m × n)
  用一维滚动数组可以降低空间复杂度为O( n)，但是对于不熟悉的题型还是老老实实用二维数组做吧。

【64】最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。
(1)确定dp数组以及下标含义：
dp[i][j]:从[0][0]到[i][j]的最小路径数字总和。
(2)确定递推公式：
dp[i][j]只能从dp[i-1][j]和dp[i][j-1]这两个方向获得，并且要获得最小路径数字总和。d[i][j] = grid[i][j]+min{dp[i-1][j],dp[i][j-1]}
(3)初始化dp数组
第一行和第一列都只有一种走法，则d[i][0]和dp[0][j]直接累加在一起就行。
for(int i =1;i<m;i++) dp[i][0] = grid[i][0] + dp[i-1][0];
for(int j =1;j<n;j++) dp[0][j] = grid[0][j] + dp[0][j-1];
(4)遍历顺序：
从上到下，从左到右
(5)举例dp数组：

坐标	0	1	2
0	1	4	5
1	2	8	6
2	6	8	7

class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size();int n = grid[0].size();vector<vector<int>> dp(m,vector<int>(n,0));dp[0][0] = grid[0][0];for(int i =1;i<m;i++) dp[i][0] = grid[i][0] + dp[i-1][0];for(int j =1;j<n;j++) dp[0][j] = grid[0][j] + dp[0][j-1];for(int i =1; i<m;i++){for(int j =1;j<n;j++){dp[i][j] = grid[i][j] + min(dp[i][j-1], dp[i-1][j]);}}return dp[m-1][n-1];}
};

【647】回文子串

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。回文字符串 是正着读和倒过来读一样的字符串。子字符串 是字符串中的由连续字符组成的一个序列。
本题可以用双指针法做，也可以用动规做（动规的空间复杂度高一点）。
（1）确定dp数组以及下标的含义
这道题，如果dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话。很难去判断递推关系，dp[i] 和 dp[i-1] ，dp[i + 1] 看上去都没啥关系。
但是我们假设知道了一个子串是回文子串的话，比如在[i,j]内是回文子串，再去看[i-1]和[j+1]是否相等，就知道是否是回文子串，换句话说，判断一个子字符串（字符串的下表范围[i,j]）是否回文，依赖于，子字符串（下表范围[i + 1, j - 1]）） 是否是回文。
dp[i] [j]：表示区间范围[i,j]的子串是否回文，dp[i] [j] =true表示回文，dp[i] [j] =false表示非回文。
（2）确定dp状态转移公式
要讨论dp[i+1][j-1]的状态：

	if(s[i] == s[j]){if(j-i<=1){//a aadp[i] [j] =true;res++;}else{//a bbc aif(dp[i+1][j-1]){//子串要是回文的s才是回文dp[i] [j] =true;res++}}}else{dp[i] [j] =false;}

（3）dp数组如何初始化
dp[i][j] = false
（4）确定遍历顺序
由于这里的dp[i+1][j-1]会决定dp[i][j]，所以遍历顺序应该是从下到上，从左到右。
（5）举例推导dp数组
以aaa为例子，因为[i,j]是一个区间则说明i<=j,二维数组下半部分全部是false，不需要管
| 坐标 | 0 | 1 | 2 |
| ---- | ---- | ---- | ---- |
| 0| 1 | 1 |1 |
| 1| 0 | 1 | 1 |
| 2 | 0 | 0 | 1 |
本题的难点是要把从数组区间上的[i][j]抽象到二维数组上，并且初始化顺序和递推公式都有变化。

class Solution {
public:int countSubstrings(string s) {int m  = s.size();int res =0;vector<vector<bool>> dp(m,vector<bool>(m,false));//优化：i<=j ，所以二维数组下半部分都不用遍历了for(int i = m-1;i>=0;i--){for(int j = i; j< m;j++){if(s[i] == s[j]){if(j-i<=1){//a aadp[i][j] = true;res++;}else{if(dp[i+1][j-1]){//这里是区间上的[i][j]dp[i][j] = true;res++;}}}else{dp[i][j] = false;}}} return res;}
};

时间复杂度o（n^2），空间复杂度o(n ^2)。

【5】最长回文子串

给你一个字符串 s，找到 s 中最长的 回文子串。
跟【647】差不多，如果是回文子串，就是要给一个变量maxlength去判断是不是最长的回文子串

class Solution {
public:string longestPalindrome(string s) {int m = s.size();int maxlen = 0;int left = 0;vector<vector<bool>> dp(m,vector<bool>(m,false));//从下到上，从左到右 [i,j]for(int i = m-1;i>=0;i--){for(int j = i;j < m;j++){if(s[i] == s[j]){if(j-i<=1){dp[i][j] = true;}else if(dp[i+1][j-1]){dp[i][j] = true;}}else{dp[i][j] = false;}//处理最长回文子串if(dp[i][j] && j-i+1>=maxlen){maxlen = j-i+1;left = i;}}}return s.substr(left,maxlen);}
};

【1143】最长公共子序列

与【718】最长重复子数组一起做。
给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。(没有指定方向)

注意：“oxcpqrsvwf”“shmtulqrypy” 最长是qr，要是单独遍历这么做还要去存储。

本来以为可以用遍历的方式做的，但是还要考虑的是求的是**最长公共子序列，一是要最长，二是要双向。**遍历的方式就有点复杂了。
这里的子序列要求有相对顺序，可以不连续。
利用动态规划：
(1)确定dp数组以及下标的含义：
dp[i][j] :长度为[0,i]的字符串text1和[0,j]的字符串text2的最长公共子序列个数;
(2) 递推公式
主要就是两大情况： text1[i] 与 text2[j]相同，text1[i] 与 text2[j ]不相同
text1[i] 与 text2[j]相同:找到公共元素：dp[i][j] = dp[i-1][j-1]+1;
text1[i] 与 text2[j]不相同：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
(3)dp数组初始化
dp[i][j] =0;
(4)dp数组遍历顺序
从递推公式可以看，有三个方向可以推导出dp[i][j]:从左到右，从上到下

遇到的问题：当我想初始化的时候，第一行和第二行需要先初始化，但是他们的初始化又要单独去遍历判断赋值，不如重新给dp[i][j]意义：表示第0-i-1的子序列和0-j-1的子序列，这样的话就可以减轻我们初始化的负担：
text1[i] 与 text2[j]也要随即向前移一个，这样才能判断[0][0]（下面的图可以很明确，第一行表示空字符和text2比较，肯定为0，同理第一列）。

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m = text1.size();int n = text2.size();vector<vector<int>> dp(m+1,vector<int>(n+1,0));for(int i =1;i<m+1;i++){for(int j =1;j<n+1;j++){if(text1[i-1] == text2[j-1]){//从0开始判断dp[i][j] = dp[i-1][j-1] +1;}else{dp[i][j] = max(dp[i-1][j],dp[i][j-1]); }}}return dp[m][n];}};

【72】 编辑距离

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作：
插入一个字符
删除一个字符
替换一个字符

利用动态规划：
(1)确定dp数组以及下标的含义：
dp[i][j] :长度为[0,i-1]的字符串word1和[0,j-1]的字符串word2的编辑距离操作数。
(2) 递推公式
在确定递推公式的时候，要考虑编辑的操作

if(word1[i-1] == word2[j-1]){
//donothing dp[i][j]  = dp[i-1][j-1];
}else{
//需要编辑距离
//增加//word2添加一个元素,相当于word1删除一个元素dp[i][j]  = dp[i-1][j]+1;
//删除//word2删除一个元素dp[i][j]  = dp[i][j-1]+1;
//换dp[i][j] = dp[i-1][j-1]+1;
//只要求这三个的最小值就行了dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1);
}

word2添加一个元素，相当于word1删除一个元素，例如 word1 = "ad" ，word2 = "a"，word1删除元素'd' 和 word2添加一个元素'd'，变成word1="a", word2="ad"， 最终的操作数是一样！ dp数组如下图所示意的：

            a                         a     d+-----+-----+             +-----+-----+-----+|  0  |  1  |             |  0  |  1  |  2  |+-----+-----+   ===>      +-----+-----+-----+a |  1  |  0  |           a |  1  |  0  |  1  |+-----+-----+             +-----+-----+-----+d |  2  |  1  |+-----+-----+

(3)dp数组初始化
dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。
那么dp[i][0] 和 dp[0][j] 表示什么呢？
dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;
同理dp[0][j] = j;
(4)dp数组遍历顺序
从递推公式可以看，有三个方向可以推导出dp[i][j]:从左到右，从上到下:

class Solution {
public:int minDistance(string word1, string word2) {int m = word1.size();int n = word2.size();vector<vector<int>> dp(m+1,vector<int>(n+1,0));//空字符，直接删除，操作数就是字符长度for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;//删除word1for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;//删除word2for(int i =1;i<m+1;i++){for(int j =1;j<n+1;j++){if(word1[i-1] == word2[j-1]){//什么都不做dp[i][j] = dp[i-1][j-1];}else{//进行增删换三种操作//删除word1//删除word2(增加word1)//替换word1或者word2dp[i][j] = min({dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1});}}}return dp[m][n];}
};

字符类的都可以考虑多构造一行一列来存放空字符。