【鸿蒙学习笔记】Stage模型工程目录
官方文档：应用配置文件概述（Stage模型）
目录标题
- `FA`模型和`Stage`模型
- 工程级目录
- 模块级目录
- app.json5
- module.json5
- 程序执行流程
- 程序基本结构
- 开发调试与发布流程
FA模型和Stage模型
工程级目录
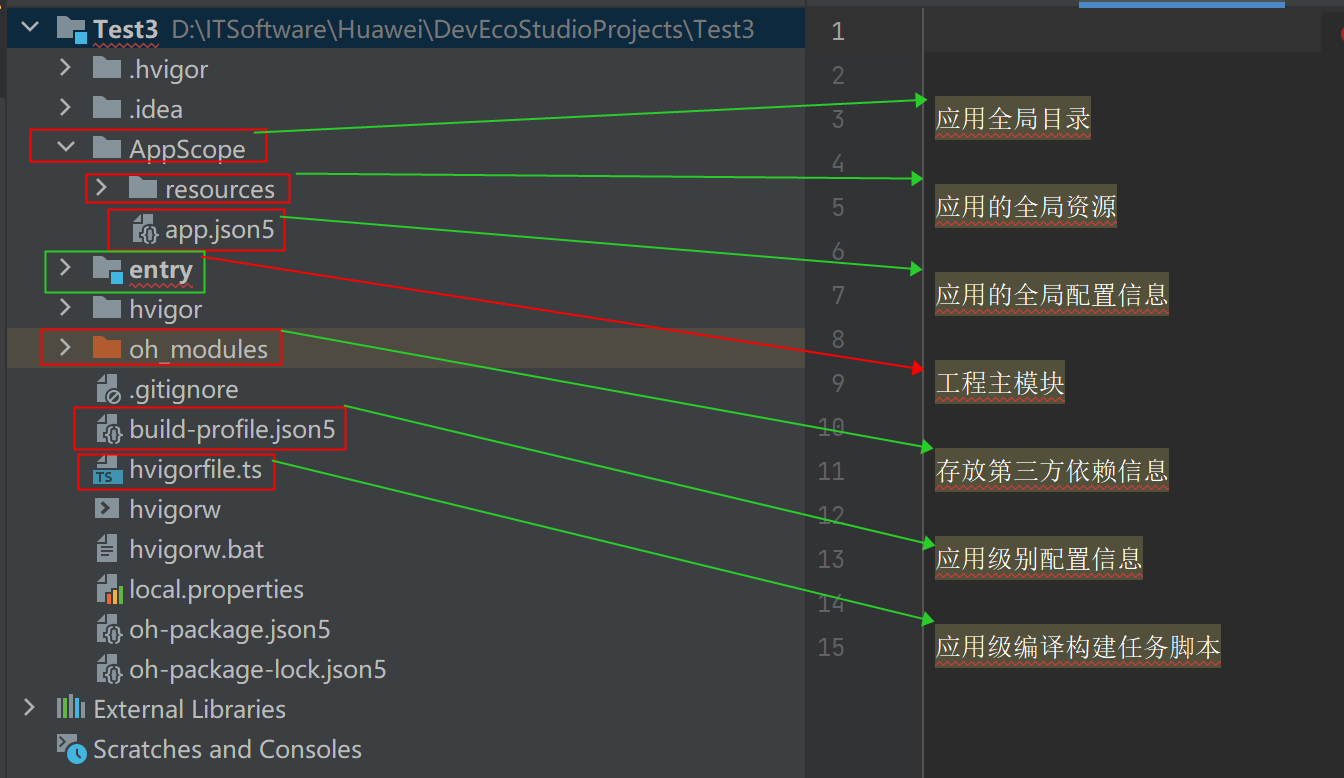
模块级目录
app.json5
官方文档：app.json5配置文件
module.json5
官方文档：module.json5配置文件
程序执行流程
-
\entry\src\main\module.json5找带有skills的Ability。
-
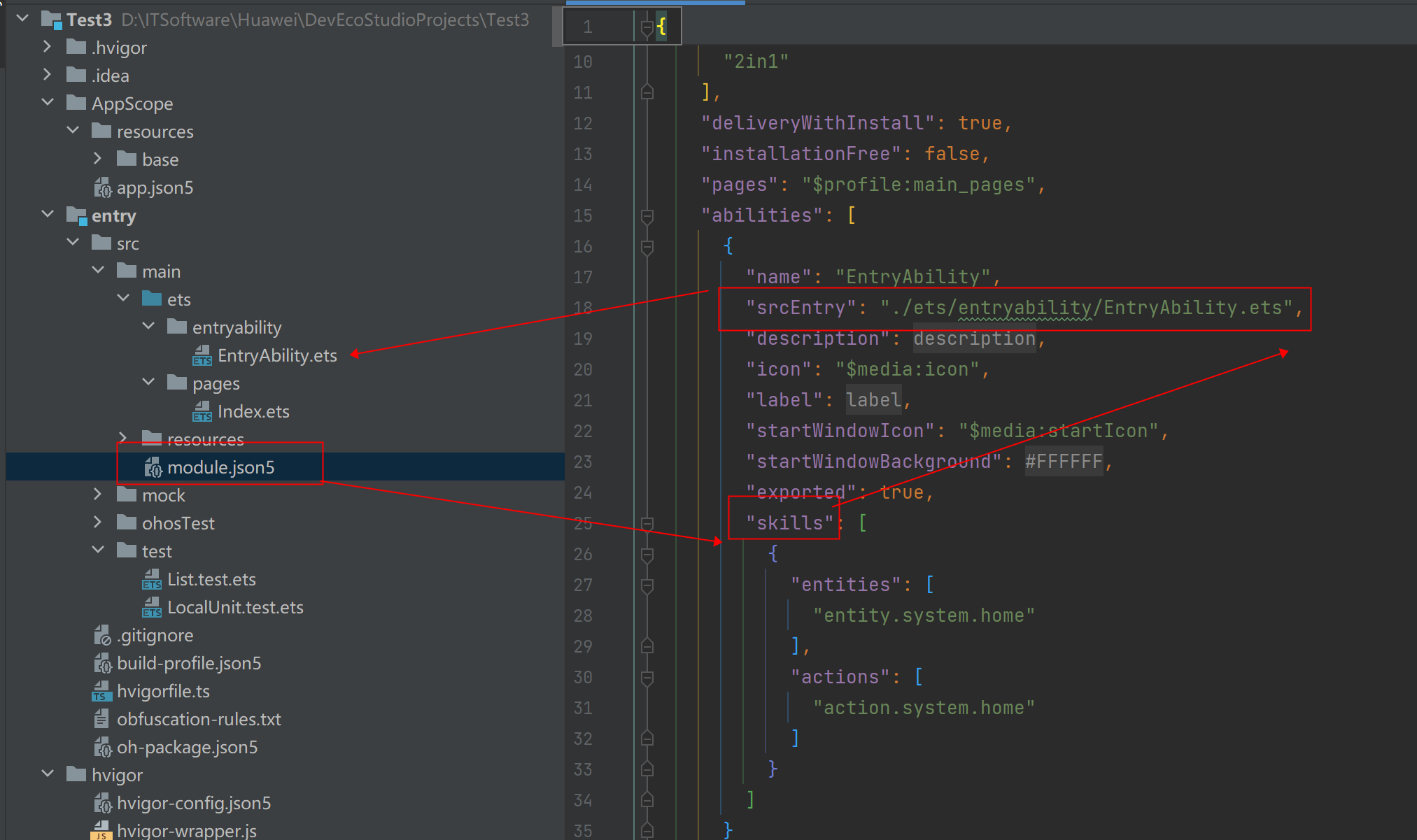
EntryAbility.ets的onWindowStageCreate调用loadContent加载pages/Index页面。
-
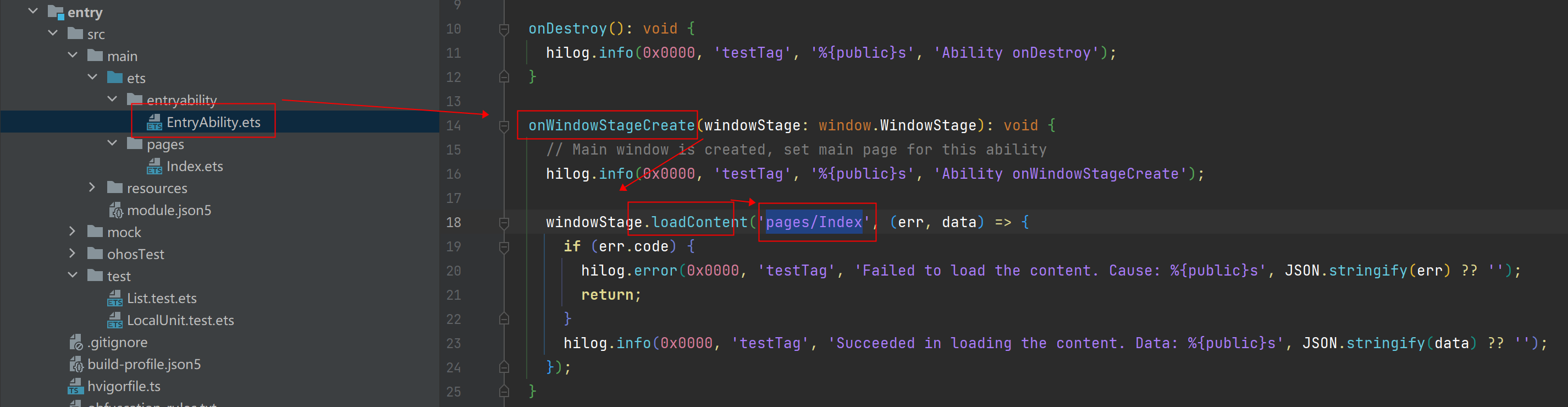
pages/Index页面含有@Entry的组件通过实现build方法来描述UI结构。
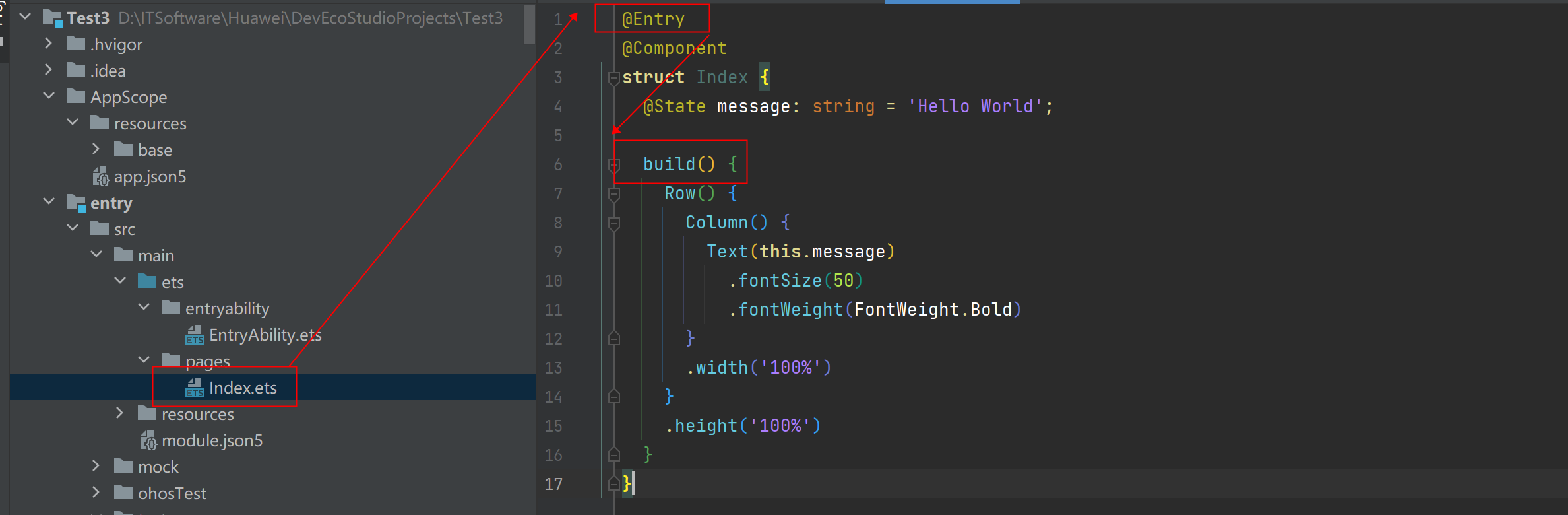
程序基本结构
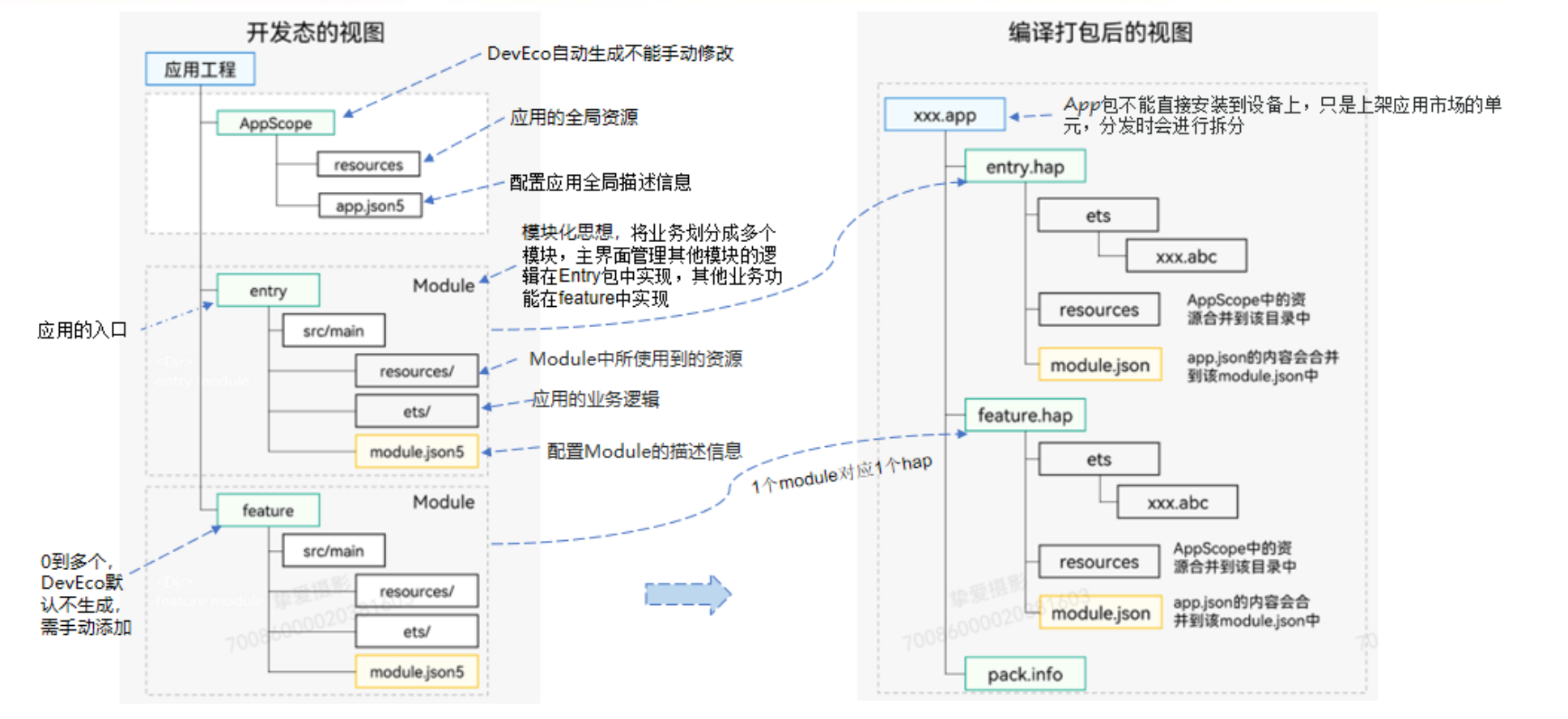
开发调试与发布流程
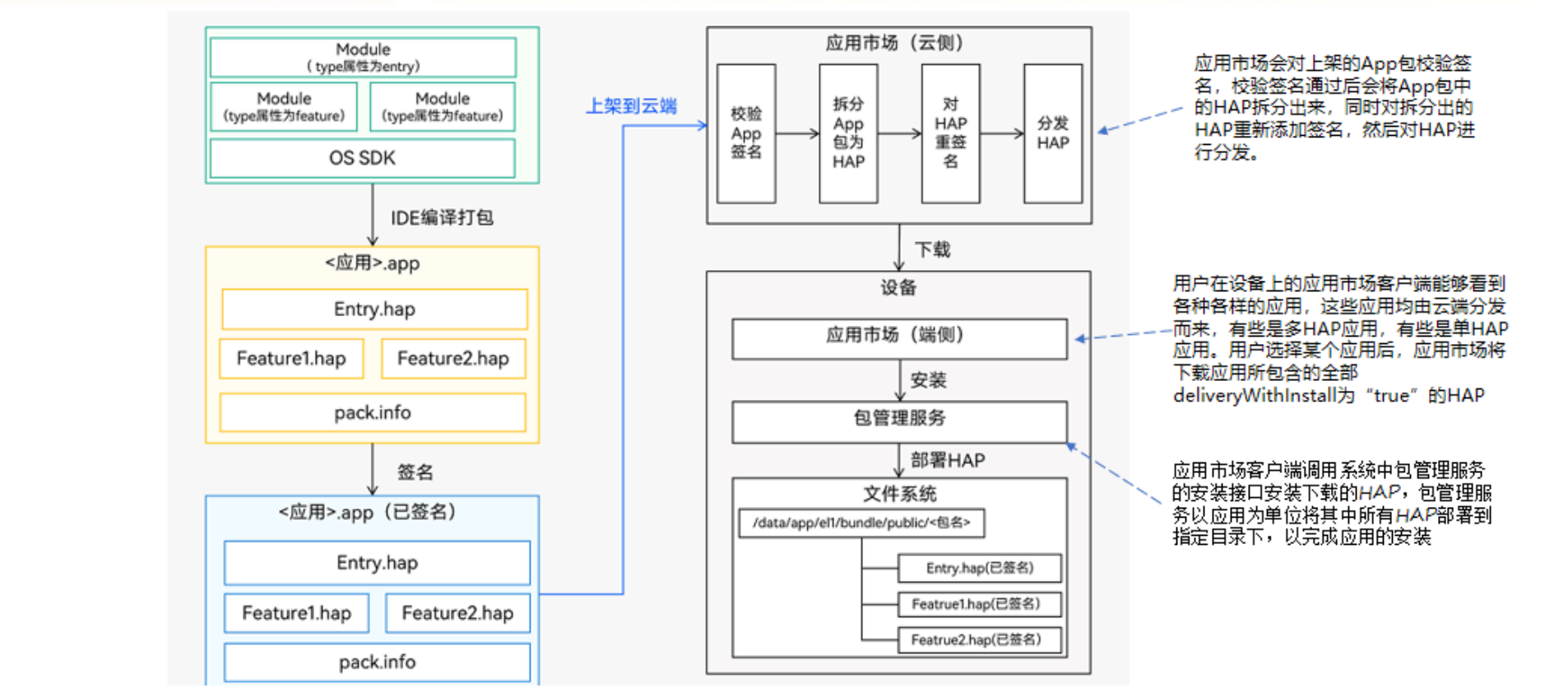
相关文章：
【鸿蒙学习笔记】Stage模型工程目录
官方文档：应用配置文件概述（Stage模型） 目录标题 FA模型和Stage模型工程级目录模块级目录app.json5module.json5程序执行流程程序基本结构开发调试与发布流程 FA模型和Stage模型 工程级目录 模块级目录 app.json5 官方文档：app.j…...
算法基础-----【动态规划】
动态规划(待完善) 动规五部曲分别为： 确定dp数组（dp table）以及下标的含义确定递推公式（状态转移公式）dp数组如何初始化确定遍历顺序举例推导dp数组、 动态规划的核心就是递归剪枝（存储键值，…...
Java中的响应式编程与Reactor框架
Java中的响应式编程与Reactor框架 大家好，我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编，也是冬天不穿秋裤，天冷也要风度的程序猿！ 响应式编程（Reactive Programming）是一种面向数据流…...
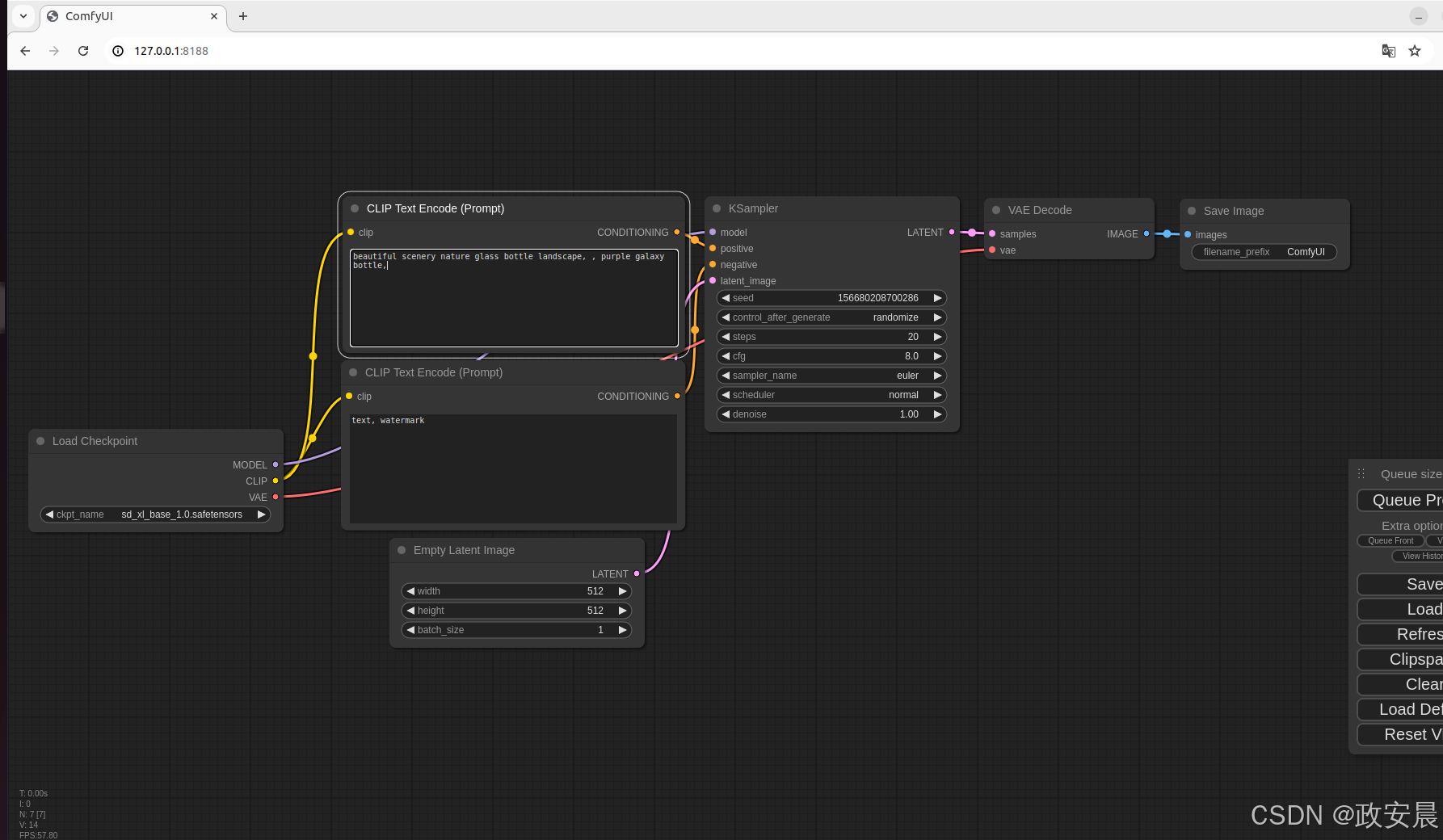
政安晨【零基础玩转各类开源AI项目】基于Ubuntu系统部署ComfyUI：功能最强大、模块化程度最高的Stable Diffusion图形用户界面和后台
目录 ComfyUI的特性介绍 开始安装 做点准备工作 在Conda虚拟环境中进行 依赖项的安装 运行 政安晨的个人主页：政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: 零基础玩转各类开源AI项目 希望政安晨的博客能够对您有所裨益，如有不足之处&…...
匿名内部类
下面代码中，Person24 是一个抽象类，这意味着它不能被直接实例化，只能通过继承它的子类来实现其抽象方法。代码片段中展示了如何使用匿名内部类来实现一个抽象类的实例。 package chapter04;public class Java24_Object_匿名内部类 {public s…...
react_web自定义组件_多类型Modal_搜索栏Search
目录 一、带输入框的Modal 二、提示框Modal 三、搜索栏Search 在做项目时引入一些现成的UI组件，但是如果和设计图冲突太大，更改时很麻烦，如果自己写一个通用组件其实也就几十分钟或者几个小时，而且更具UI设计更改也比较好更改&…...
Apache Flink架构介绍
目录 一、Apache Flink架构组件栈 1.1 概述 1.2 架构图 1.3 架构分层组件说明 1.3.1 物理部署层 1.3.2 Runtime 核心层 1.3.3 API & Libraries层 二、Flink运行时架构 2.1 概述 2.2 架构图 2.3 架构角色和组件 2.3.1 Flink Clients客户端 2.3.2 JobManager 2.…...
华为HCIP Datacom H12-821 卷28
1.单选题 下面是一台路由器的部分配置，关于该部分配置描述正确的是，[HUAWEI]ip ip-prefx pl permit 10.0.192.0 8greater-equal17 less-equal 18 A、10.0.192.0/8网段内，掩码长度为18的路由会匹配到该前缀列表，匹配规则为允许 B、10.0.192.0/8网段内掩码长度为21的路…...
安装Nginx以及简单使用 —— windows系统
一、背景 Nginx是一个很强大的高性能Web和反向代理服务，也是一种轻量级的Web服务器，可以作为独立的服务器部署网站，应用非常广泛，特别是现在前后端分离的情况下。而在开发过程中，我们常常需要在window系统下使用Nginx作…...
【UE5.3】笔记8 添加碰撞，检测碰撞
添加碰撞 打开BP_Food,添加Box Collision组件，与unity类似： 调整Box Collision的大小到刚好包裹物体，通过调整缩放和盒体范围来控制大小，一般先调整缩放找个大概大小，然后调整盒体范围进行微调。 碰撞检测 添加好碰撞…...
丝滑流畅！使用kimi快速完成论文仿写
学境思源，一键生成论文初稿： AcademicIdeas - 学境思源AI论文写作 今天的分享，我们将带大家探索一种新的学术写作技巧——使用Kimi进行论文仿写。本文将深入解析如何利用Kimi的智能辅助功能，提高论文写作的效率和质量，…...
【C++】认识使用string类
【C】STL中的string类 C语言中的字符串标准库中的string类string类成员变量string类的常用接口说明成员函数string(constructor构造函数)~string(destructor析构函数)默认赋值运算符重载函数 遍历string下标[ ]迭代器范围for反向迭代器 capacitysizelengthmax_sizeresizecapaci…...
如何在 Odoo 16 中对 Many2Many 字段使用 Group by
Many2many 字段与 Many2one 字段类似，因为它们在模型之间建立了新的关系。在Odoo 16中，您无法按 many2many 字段分组，因为可以使用 many2many 记录选择任何记录。当您使用 many2many 字段给出 group by 过滤器时，您将遇到断言错误。 介绍如何在 Odoo 16 中使用 Many2Many…...
PCL从理解到应用【03】KDTree 原理分析 | 案例分析 | 代码实现
前言 本文分析KDTree的原理，集合案例深入理解，同时提供源代码。 三个案例：K近邻搜索、半径内近邻搜索、近似最近邻搜索。方法对比，如下表所示： 特性K近邻搜索半径内近邻搜索近似最近邻搜索描述查找K个最近邻点查找指…...
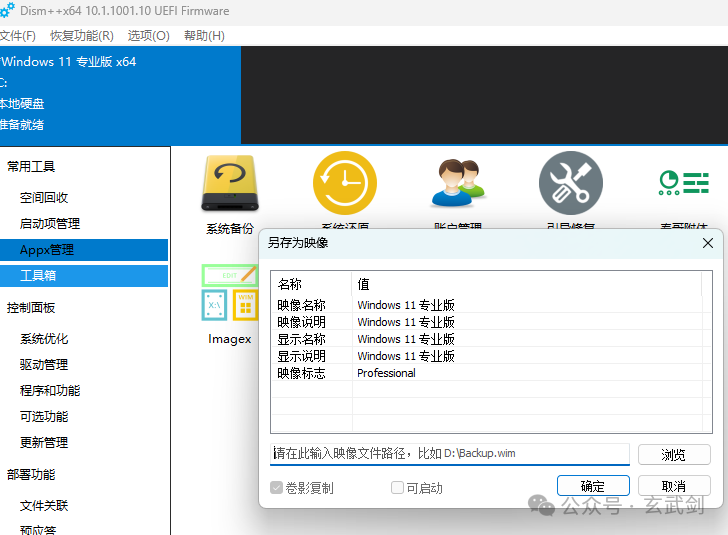
Windows 11内置一键系统备份与还原 轻松替代Ghost
面对系统崩溃、恶意软件侵袭或其他不可预见因素导致的启动失败，Windows 7~Windows 11内置的系统映像功能能够迅速将您的系统恢复至健康状态，确保工作的连续性和数据的完整性。 Windows内置3种备份策略 U盘备份：便携且安全 打开“创建一个恢…...
leetCode-hot100-动态规划专题
动态规划 动态规划定义动态规划的核心思想动态规划的基本特征动态规划的基本思路例题322.零钱兑换53.最大子数组和72.编辑距离139.单词拆分62.不同路径63.不同路径Ⅱ64.最小路径和70.爬楼梯121.买卖股票的最佳时机152.乘积最大子数组 动态规划定义 动态规划（Dynami…...
【算法笔记自学】入门篇（2）——算法初步
4.1排序 自己写的题解 #include <stdio.h> #include <stdlib.h>void selectSort(int A[], int n) {for(int i 0; i < n - 1; i) { // 修正索引范围int k i;for(int j i 1; j < n; j) { // 修正索引范围if(A[j] < A[k]) {k j;}}if (k ! i) { // 仅在…...
Redis基础教程（六）：redis 哈希(Hash)
💝💝💝首先，欢迎各位来到我的博客，很高兴能够在这里和您见面！希望您在这里不仅可以有所收获，同时也能感受到一份轻松欢乐的氛围，祝你生活愉快！ 💝Ὁ…...
鸿蒙开发设备管理：【@ohos.account.appAccount (应用帐号管理)】
应用帐号管理 说明： 本模块首批接口从API version 7开始支持。后续版本的新增接口，采用上角标单独标记接口的起始版本。开发前请熟悉鸿蒙开发指导文档：gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 导入模…...
java项目自定义打印日志，打印请求方式，参数用时等
1.相关依赖 <!-- 私人工具包 --><dependency><groupId>cn.changeforyou</groupId><artifactId>location</artifactId><version>1.13-SNAPSHOT</version></dependency><!-- hutool工具依赖 --><dependency>…...
ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...
为什么需要建设工程项目管理？工程项目管理有哪些亮点功能？
在建筑行业，项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升，传统的管理模式已经难以满足现代工程的需求。过去，许多企业依赖手工记录、口头沟通和分散的信息管理，导致效率低下、成本失控、风险频发。例如&#…...
Linux云原生安全：零信任架构与机密计算
Linux云原生安全：零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言：云原生安全的范式革命 随着云原生技术的普及，安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测，到2025年，零信任架构将成为超…...
华为云Flexus+DeepSeek征文｜DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文｜DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色，华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型，能助力我们轻松驾驭 DeepSeek-V3/R1，本文中将分享如何…...
C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如，已知表达式3*52，依照子表达式的求值顺序，有两种可能的结果，如图9-3所示。 如果乘法先执行，结果是17。如果5…...
【C++】纯虚函数类外可以写实现吗？
1. 答案 先说答案，可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码：HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
起重机起升机构的安全装置有哪些？
起重机起升机构的安全装置是保障吊装作业安全的关键部件，主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理： 一、超载保护装置（核心安全装置） 1. 起重量限制器 功能：实时监测起升载荷&a…...
Linux中INADDR_ANY详解
在Linux网络编程中，INADDR_ANY 是一个特殊的IPv4地址常量（定义在 <netinet/in.h> 头文件中），用于表示绑定到所有可用网络接口的地址。它是服务器程序中的常见用法，允许套接字监听所有本地IP地址上的连接请求。 关…...
[C++错误经验]case语句跳过变量初始化
标题：[C错误经验]case语句跳过变量初始化 水墨不写bug 文章目录 一、错误信息复现二、错误分析三、解决方法 一、错误信息复现 write.cc:80:14: error: jump to case label80 | case 2:| ^ write.cc:76:20: note: crosses initialization…...