【C++题解】1561. 买木头
问题:1561. 买木头
类型:省赛、数组问题、二分答案、贪心、2015江苏省青少年信息学奥林匹克竞赛复赛
题目描述:
有 n 个木材供应商,每个供货商有长度相同一定数量的木头。长木头可以锯短,但短木头不能接长。有一个客人要求 m 根长度相同的木头。要求计算出,此时供货商提供的木头满足客人要求的最长的长度是多少。
例如 n=2,m=30,两个供货商的木头为
12,10 第 1 个供货商的木头长度为 12 ,共有 10 根;
5,10 第 2 个供货商的木头长度为 5 ,共有 10 根。
计算的结果为 5 ,即长度为 12 的木头一根可锯出两根长度为 5 的木头,多余的无用,长度为 5 的木头不动,此时可得到 30 根长度为 5 的木头。
输入:
整数 n,m,L1,S1 (1≤n≤10000,1≤m≤1000000,1≤L1≤10000,1≤S1≤100)
其中 L1 是第一个供货商木头的长,S1 是第一个供货商木头数量。其他供货商木头的长度和数量 Li 和 Si(i≥2),由下面的公式给出:
Li=((Li−1×37011+10193)mod10000)+1
Si=((Si−1×73011+24793)mod100)+1
输出:
一个整数,即满足要求的 m 根长度相同的木头的最大长度。
样例:
输入:
10 10000 8 20
输出:
201

完整代码如下:
#include<bits/stdc++.h>
using namespace std;int m,cmax=0;
vector<int> v;bool cmp(int a,int b){return a>b;
}int findNum(int mid){int c=0,t;for(int i=0;i<v.size();i++){t=v[i];while(t>=mid){++c;t-=mid;} }return c;
}void myFind(int l,int r){if(l>r){return;}int mid;mid=l+r>>1;if(m>findNum(mid)){return myFind(l,mid-1);}else{cmax=mid;return myFind(mid+1,r);}}
int main(){//一、分析问题//已知:有n个木材供应商。需要m 根长度相同的木头。L 是第一个供货商木头的长,S是第一个供货商木头数量。 //未知:供货商提供的木头满足客人要求的最长的长度是多少。//关系:长木头可以锯短,但短木头不能接长。其他供货商木头的长度和数量 Li 和 Si(i≥2),由下面的公式给出://Li=((Li-1×37011+10193)mod10000)+1//Si=((Si-1×73011+24793)mod100)+1//二、数据定义 int n,li,si;//三、数据输入cin>>n>>m>>li>>si; for(int i=0;i<n;i++){for(int j=0;j<si;j++){v.push_back(li);} li=(li*37011+10193)%10000+1;si=(si*73011+24793)%100+1;}//四、数据计算 sort(v.begin(),v.end(),cmp);myFind(1,v[0]);//五、输出结果 cout<<cmax;return 0;
}相关文章:

【C++题解】1561. 买木头
问题:1561. 买木头 类型:省赛、数组问题、二分答案、贪心、2015江苏省青少年信息学奥林匹克竞赛复赛 题目描述: 有 n 个木材供应商,每个供货商有长度相同一定数量的木头。长木头可以锯短,但短木头不能接长。有一个客…...

解决android native包webview,webview中的请求blocked by CORS policy
在stack overflow查,差不多查到的都是些webView.getSettings().setxxx,没用。在github上找别的类似的android native包webview运行pwa的项目,把它们的webView.getSettings().setxxx全搬过来,写了有一页多,一个有用的都…...

链篦机回转窑球团生产工艺
生球在回转窑氧化焙烧,回转窑头部设有燃烧器,燃料可以采用气体、固体、液体。 来自环冷机一冷却段的高温废气作为二次风进入窑内参与燃烧,烧成成品球进入环冷机。 环冷机采用鼓风冷却,热风风箱分为四段: 一段气体引至…...

查看电脑ip地址快捷键是什么?是哪个
在网络世界中,IP地址是每个网络设备的唯一标识,无论是我们的电脑、手机还是其他联网设备,都需要一个独特的IP地址来进行通讯。在日常生活和工作中,我们有时需要查看电脑的IP地址,以便进行网络设置、故障排查或远程连接…...
】)
面试专区|【54道Spring Cloud高频题整理(附答案背诵版)】
什么是Spring Cloud? Spring Cloud是一个基于Spring Boot的开源框架,它提供了在分布式系统中集成各种服务治理功能的工具,如配置管理、服务发现、断路器、智能路由、微代理、控制总线、全局锁、决策竞选、分布式会话和集群状态等。其主要目…...

Shopee(虾皮)怎么获取流量?
店铺流量的高低会直接关联到卖家店铺单量,也关系到一个店铺的营业情况和利润,那么Shopee的流量从哪里来呢? Shopee的平台流量可分为五个部分: 1.自然流量 2.关键字广告流量 3.平台活动流量 4.营销流量 5.粉丝流量 怎么提升…...
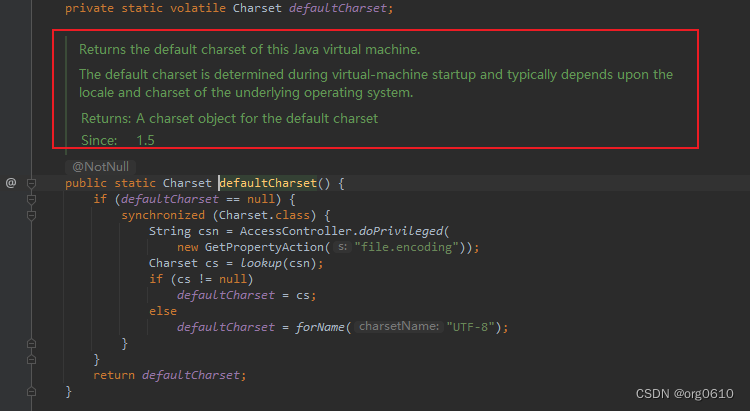
Java启动虚拟机默认字符集编码
-Dfile.encodingUTF-8 java程序启动默认字符集编码参数 // 这里会创建一个Charset.defaultCharset().name()的流,在Windows命令行窗口启动,会出现字符编码为GBK的情况 // 导致乱码输入、输出都会有影响 // 解决办法流的读取指定编码new InputStreamRead…...

【单片机编程模式】状态机编程
状态机编程是一种编程模式,它基于有限状态机(Finite State Machine,简称FSM)的概念。以下是状态机编程的清晰解释,分点表示和归纳: 基本概念: 状态机是一个有向图形,由一组节点&…...

IPSS模块怎么安装到VOS服务器的,到底有没有效果,是不是能大幅度提升VOS3000安全性呢
由于VOS的普及性,不得不承认VOS确实是非常优秀的软交换,但是很多客户在使用过程中都会遇到各种安全问题,比如话费被盗用了,历史话单一堆的非法呼叫话单,严重的影响到了话务安全,并不是那点话费的事了&#…...

C++ STL容器:序列式容器-堆pirority_queue
摘要: CC STL(Standard Template Library,标准模板库)在C编程中的重要性不容忽视,STL提供了一系列容器、迭代器、算法和函数对象,这些组件极大地提高了C程序的开发效率和代码质量。 STL 容器 分为 2 大类 …...

ECharts在最新版本中使用getInstanceByDom报错处理
引用问题导致报错 如果按如下引用的话,会报错 import echarts from “echarts/lib/echarts”; 原因 在 ECharts 的之前版本中,默认导出了一个名为 echarts 的对象,所以使用 import echarts from “echarts” 是没有问题的。但是在 ECharts …...

利用C语言实现三子棋游戏
文章目录 1.游戏界面2.游戏内容2.1 棋盘类型2.2棋盘的初始化2.3 打印棋盘的界面展示 3.游戏操作3.1 玩家操作3.2 电脑操作3.3 胜负判定 4.代码整合 1.游戏界面 无论写任何程序,我们都需要先去了解它的大概框架,这里我们先把它的初始界面写出来。一个游戏…...

大学教师门诊预约小程序-计算机毕业设计源码73068
摘要 在当今数字化、信息化的浪潮中,大学校园的服务管理正朝着智能化、便捷化的方向迈进。为了优化大学教师的医疗体验,提升门诊预约的效率和便捷性,我们基于Spring Boot框架设计并实现了一款大学教师门诊预约小程序。该小程序不仅提供了传统…...

Python PyCryptodome库介绍与实例
Python PyCryptodome库介绍与实例 1. 安装2. 基本概念3. 使用场景和示例代码3.1 对称加密 - AES3.2 非对称加密 - RSA3.3 哈希函数 - SHA2563.4 消息认证码 - HMAC 4. 总结 PyCryptodome是一个强大的Python加密库,提供了各种加密算法和工具。本文将介绍PyCryptodome的基本概念和…...

《框架封装者 · 自定义初始化事件》
📢 大家好,我是 【战神刘玉栋】,有10多年的研发经验,致力于前后端技术栈的知识沉淀和传播。 💗 🌻 CSDN入驻不久,希望大家多多支持,后续会继续提升文章质量,绝不滥竽充数…...

ActiViz实战:使用vtkImageClip和vtkImageActor根据滑动条来显示当前图像数据切面
文章目录 一、效果预览二、代码实现三、源码地址一、效果预览 ActiViz实现图像数据切面显示 二、代码实现 public partial class Form1 : Form {private vtkRenderWindowInteractor _interactor;private vtkRenderer _renderer...

【论文笔记】BEVCar: Camera-Radar Fusion for BEV Map and Object Segmentation
原文链接:https://arxiv.org/abs/2403.11761 0. 概述 本文的BEVCar模型是基于环视图像和雷达融合的BEV目标检测和地图分割模型,如图所示。模型的图像分支利用可变形注意力,将图像特征提升到BEV空间中,其中雷达数据用于初始化查询…...

圆通寄15kg30kg一般多少钱?寄大件物品怎么寄最便宜?
作为一名即将毕业的大学生,搬家成了我和室友们共同的难题。尤其是在寄送大件物品时,如何省钱、如何打包、选择哪家快递公司等问题让我们头疼不已。今天,我就来分享一些寄大件物品的省钱技巧以及打包方法,希望对大家有所帮助。 一…...

transformer初探
transformer初探 self-attentionmultihead-attentionencoderdecoder self-attention 其实就是三个矩阵, W q W_q Wq、 W k W_k Wk、 W v W_v Wv,这三个矩阵就是需要训练的参数。分别得到每个token对应的 q q q k k k v v v,其中 q …...

JUC并发编程基础(包含线程概念,状态等具体实现)
一.JUC并发编程基础 1. 并行与并发 1.1 并发: 是在同一实体上的多个事件是在一台处理器上"同时处理多个任务"同一时刻,其实是只有一个事件在发生. 即多个线程抢占同一个资源. 1.2 并行 是在不同实体上的多个事件是在多台处理器上同时处理多个任务同一时刻,大家…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...
