成人高考报名条件及收费标准详解
成人高考报名条件及收费标准详解
您想通过成人高考改变自己的命运,但不知道报名条件和收费标准?本文将为您详细介绍成人高考报名条件和收费标准,并为您提供专业的成人教育服务。
深圳成人高考www.shenzhixun.com

成人高考报名条件
成人高考报名条件主要包括三方面:年龄、学历和身体条件。
首先,年龄方面,报名者必须年满18周岁,具有完全民事行为能力。
其次,学历方面,报名者可以是高中毕业生、中专毕业生或同等学历的学生。
最后,身体条件方面,报名者必须身体健康,能够参加高考和学习。
成人高考收费标准
成人高考收费标准根据地区和学校的不同而异。一般来说,成人高考报名费为100-500元人民币,考试费为50-200元人民币。
深职训学校解决问题
您在成人高考报名和学习过程中遇到了问题?深职训学校为您提供专业的成人教育服务。
我们拥有经验丰富的教师和专业的教学设施,能够为您提供高质量的成人教育服务。
我们的成人高考报名服务包括:报名指导、考试培训、学习规划等。
同时,我们还提供了成人高考复习班,包括:课程设计、教学实施、学习监控等。
如果您在成人高考报名和学习过程中遇到了问题,随时找我们交流,我们很愿意听取并分享我们的经验。
深职训学校,您的成人教育合作伙伴。
相关文章:

成人高考报名条件及收费标准详解
成人高考报名条件及收费标准详解 您想通过成人高考改变自己的命运,但不知道报名条件和收费标准?本文将为您详细介绍成人高考报名条件和收费标准,并为您提供专业的成人教育服务。 深圳成人高考www.shenzhixun.com 成人高考报名条件 成人高考…...
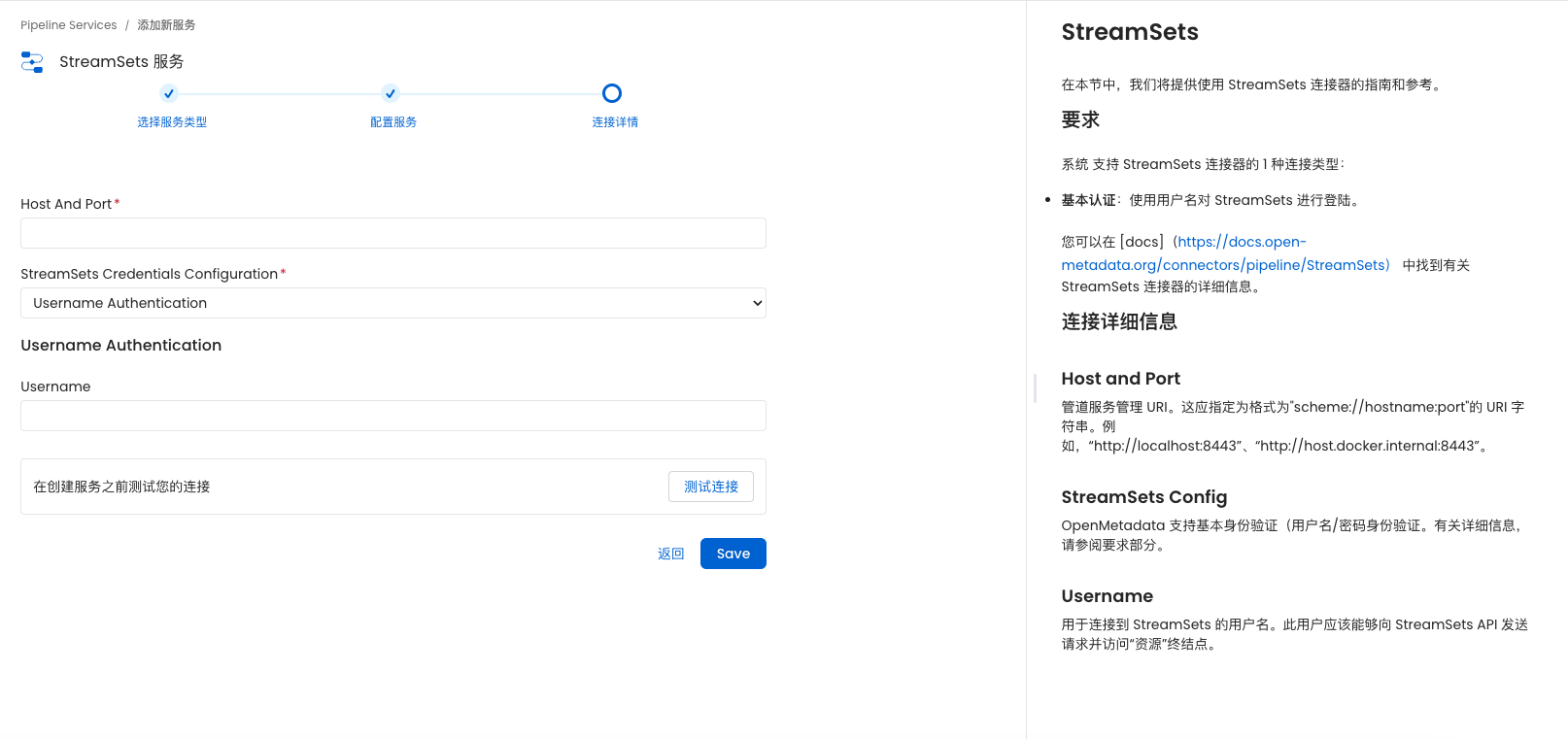
openmetadata1.3.1 自定义连接器 开发教程
openmetadata自定义连接器开发教程 一、开发通用自定义连接器教程 官网教程链接: 1.https://docs.open-metadata.org/v1.3.x/connectors/custom-connectors 2.https://github.com/open-metadata/openmetadata-demo/tree/main/custom-connector (一&…...

PostgreSQL 如何优化存储过程的执行效率?
文章目录 一、查询优化1. 正确使用索引2. 避免不必要的全表扫描3. 使用合适的连接方式4. 优化子查询 二、参数传递1. 避免传递大对象2. 参数类型匹配 三、减少数据量处理1. 限制返回结果集2. 提前筛选数据 四、优化逻辑结构1. 分解复杂的存储过程2. 避免过度使用游标 五、事务处…...

普中51单片机:数码管显示原理与实现详解(四)
文章目录 引言数码管的结构数码管的工作原理静态数码管电路图开发板IO连接图代码演示 动态数码管实现步骤数码管驱动方式电路图开发板IO连接图真值表代码演示1代码演示2代码演示3 引言 数码管(Seven-Segment Display)是一种常见的显示设备,广…...
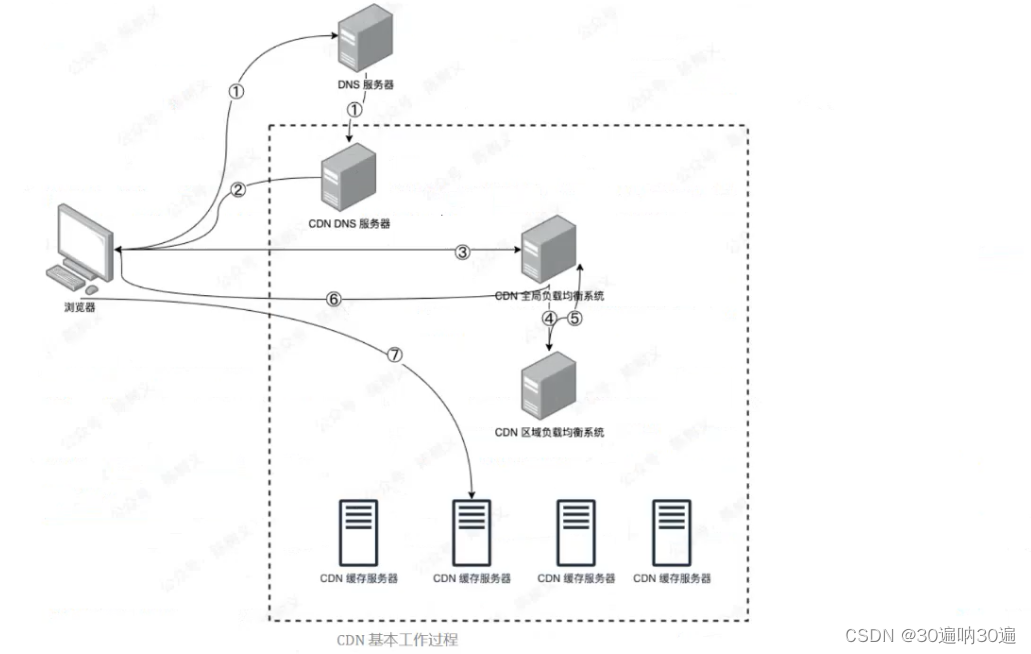
web缓存代理服务器
一、web缓存代理 web代理的工作机制 代理服务器是一个位于客户端和原始(资源)服务器之间的服务器,为了从原始服务器取得内容,客户端向代理服务器发送一个请求,并指定目标原始服务器,然后代理服务器向原始…...

容器:queue(队列)
以下是关于queue容器的总结 1、构造函数:queue [queueName] 2、添加、删除元素: push() 、pop() 3、获取队头/队尾元素:front()、back() 4、获取栈的大小:size() 5、判断栈是否为空:empty() #include <iostream> #include …...

探索 WebKit 的后台同步新纪元:Web Periodic Background Synchronization 深度解析
探索 WebKit 的后台同步新纪元:Web Periodic Background Synchronization 深度解析 随着 Web 应用逐渐成为我们日常生活中不可或缺的一部分,用户对应用的响应速度和可靠性有了更高的期待。Web Periodic Background Synchronization API(周期…...

ctfshow web入门 web338--web344
web338 原型链污染 comman.js module.exports {copy:copy };function copy(object1, object2){for (let key in object2) {if (key in object2 && key in object1) {copy(object1[key], object2[key])} else {object1[key] object2[key]}}}login.js var express …...

mupdf加载PDF显示中文乱码
现象 加载PDF显示乱码,提示非嵌入字体 non-embedded font using identity encoding调式 在pdf-font.c中加载字体 调试源码发现pdf文档的字体名字居然是GBK,估计又是哪个windows下写的pdf生成工具生成pdf 字体方法: static pdf_font_desc * load_cid…...

常用的限流工具Guava RateLimiter 或Redisson RRateLimiter
在分布式系统和高并发场景中,限流是一个非常常见且重要的需求。以下是一些常用的限流工具和库,包括它们的特点和使用场景: 1. Guava RateLimiter Google 的 Guava 库中的 RateLimiter 是一个简单且高效的限流工具,适用于单节点应…...
和循环神经网络(RNN) 的区别与联系)
卷积神经网络(CNN)和循环神经网络(RNN) 的区别与联系
卷积神经网络(CNN)和循环神经网络(RNN)是两种广泛应用于深度学习的神经网络架构,它们在设计理念和应用领域上有显著区别,但也存在一些联系。 ### 卷积神经网络(CNN) #### 主要特点…...

Unity【入门】场景切换和游戏退出及准备
1、必备知识点场景切换和游戏退出 文章目录 1、必备知识点场景切换和游戏退出1、场景切换2、鼠标隐藏锁定相关3、随机数和自带委托4、模型资源的导入1、模型由什么构成2、Unity支持的模型格式3、如何指导美术同学导出模型4、学习阶段在哪里获取模型资源 2、小项目准备工作需求分…...

Python 函数递归
以下是一个使用递归计算阶乘的 Python 函数示例 : 应用场景: 1. 动态规划问题:在一些需要逐步求解子问题并利用其结果的动态规划场景中,递归可以帮助直观地表达问题的分解和求解过程。 2. 遍历具有递归结构的数据:如递…...
如何配置 MyBatis 实现打印可执行的 SQL 语句)
MyBatis(27)如何配置 MyBatis 实现打印可执行的 SQL 语句
在开发过程中,打印可执行的SQL语句对于调试和性能优化是非常有帮助的。MyBatis提供了几种方式来实现SQL语句的打印。 1. 使用日志框架 MyBatis可以通过配置其内部使用的日志框架(如Log4j、Logback等)来打印SQL语句。这是最常用的方法。 Lo…...

3.js - 裁剪平面(clipIntersection:交集、并集)
看图 代码 // ts-nocheck// 引入three.js import * as THREE from three// 导入轨道控制器 import { OrbitControls } from three/examples/jsm/controls/OrbitControls// 导入lil.gui import { GUI } from three/examples/jsm/libs/lil-gui.module.min.js// 导入tween import …...

在5G/6G应用中实现高性能放大器的建模挑战
来源:Modelling Challenges for Enabling High Performance Amplifiers in 5G/6G Applications {第28届“集成电路和系统的混合设计”(Mixed Design of Integrated Circuits and Systems)国际会议论文集,2021年6月24日至26日,波兰洛迪} 本文讨…...

Perl 数据类型
Perl 数据类型 Perl 是一种功能丰富的编程语言,广泛应用于系统管理、网络编程、GUI 开发等领域。在 Perl 中,数据类型是编程的基础,决定了变量存储信息的方式以及可以对这些信息执行的操作。本文将详细介绍 Perl 中的主要数据类型࿰…...

网络协议 -- IP、ICMP、TCP、UDP字段解析
网络协议报文解析及工具使用介绍 1. 以太网帧格式及各字段作用 -------------------------------- | Destination MAC Address (48 bits) | -------------------------------- | Source MAC Address (48 bits) …...

【工具】豆瓣自动回贴软件
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,欢迎[点赞、收藏、关注]哦~ 相比于之前粗糙丑陋的黑命令框版本,这个版本新增了UI界面,从此可以不需要再挨个去翻配置文件了。 另外,升级了隐藏浏…...

初学Spring之动态代理模式
动态代理和静态代理角色一样 动态代理的代理类是动态生成的 动态代理分为两大类: 基于接口的动态代理(JDK 动态代理)、基于类的动态代理(cglib) 也可以用 Java 字节码实现(Javassist) Prox…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
