Codeforces Round #956 (Div. 2) and ByteRace 2024(A~D题解)
这次比赛也是比较吃亏的,做题顺序出错了,先做的第三个,错在第三个数据点之后,才做的第二个(因为当时有个地方没检查出来)所以这次比赛还是一如既往地打拉了
那么就来发一下题解吧
A. Array Divisibility


题意:对于1<=k<=n,对于每个k其倍数下标之和一定为k的倍数
思路:直接从1赋值到n就行,也是水题一个
#include<bits/stdc++.h>
using namespace std;
#define int long long
int t;
int n;
signed main()
{cin>>t;while(t--){cin>>n;for(int i=1;i<=n;i++){cout<<i<<" ";}cout<<"\n";}return 0;
}
B. Corner Twist



题意:就是给你两个数组,问你两个数组能否按照题上所说的方法相互转换得到
思路:将整个大矩阵拆成2*2的小矩阵,然后每次只要让左上角那个和下面的变成一样就可以,然后我们最后原本只需要检查最后一列和最后一行是否相同就可以(ps:我写的是逐一比较,因为比较好写)(错了一次是因为比较的时候内层循环写成n了)
#include<bits/stdc++.h>
using namespace std;
#define int long long
int t;
int n,m;
char a[505][505];
char b[505][505];
signed main()
{cin>>t;while(t--){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>b[i][j];}}for(int i=1;i<=n-1;i++){for(int j=1;j<=m-1;j++){int cha = ((b[i][j]-'0')-(a[i][j]-'0')+3)%3;if(cha==1){a[i][j]=(a[i][j]+1)%3+'0';a[i+1][j+1]=(a[i+1][j+1]+1)%3+'0';a[i+1][j]=(a[i+1][j]+2)%3+'0';a[i][j+1]=(a[i][j+1]+2)%3+'0';}else if(cha==2){a[i][j]=(a[i][j]+2)%3+'0';a[i+1][j+1]=(a[i+1][j+1]+2)%3+'0';a[i+1][j]=(a[i+1][j]+1)%3+'0';a[i][j+1]=(a[i][j+1]+1)%3+'0';}}}int flag=1;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]==b[i][j]){continue;}elseflag=0;}}if(flag==0){cout<<"NO"<<"\n";}else{cout<<"YES"<<"\n";}}return 0;
}C. Have Your Cake and Eat It Too



题意:就说有一个蛋糕 ,被分成了许多块,然后三个人对每部分的蛋糕都有一个自己的价值,但是所有块的价值总和是一定的,然后问你如何划分这个区间,才能满足每个区间都大于(tot+2)/3
思路:对六种情况分别贪心即可,先让两边的取到比sum大的位置,然后再看中间的是否比sum大,是的话就直接输出,如果都不满足,最后就只能输出-1了
#include<bits/stdc++.h>
using namespace std;
#define int long long
signed main()
{int t;cin>>t;while(t--){int n;cin >> n;int a[n+1], b[n+1], c[n+1];int sum = 0;for(int i = 1;i<=n;i++){cin >> a[i];sum += a[i];}sum = (sum+2)/3;//题中说了上限除法 for(int i = 1;i<=n;i++){cin >> b[i];}for(int i = 1;i<=n;i++){cin >> c[i];}vector<int> p1(n+5), p2(n+5), p3(n+5);//正序前缀和 vector<int> s1(n+5), s2(n+5), s3(n+5);//倒序前缀和 for(int i = 1; i <= n; i++){p1[i] = p1[i-1] + a[i];p2[i] = p2[i-1] + b[i];p3[i] = p3[i-1] + c[i];}for(int i = n; i >= 1; i--){s1[i] = s1[i+1] + a[i];s2[i] = s2[i+1] + b[i];s3[i] = s3[i+1] + c[i];}//a b c int i = 1, j = n;while(p1[i-1] < sum && i <= n){i++;}while(s3[j+1] < sum && j >= 1){j--;}if(i <= j && p2[j]-p2[i-1] >= sum){cout << 1 << ' ' << i-1 << ' ' << i << ' ' << j << ' ' << j+1 << ' ' << n << endl;continue;}// a c bi = 1, j = n;while(p1[i-1] < sum && i <= n){i++;}while(s2[j+1] < sum && j >= 1){j--;}if(i <= j && p3[j]-p3[i-1] >= sum){cout << 1 << ' ' << i-1 << ' ' << j+1 << ' ' << n << ' ' << i << ' ' << j << endl;continue;}// b c ai = 1, j = n;while(p2[i-1] < sum && i <= n){i++;}while(s1[j+1] < sum && j >= 1){j--;}if(i <= j && p3[j]-p3[i-1] >= sum){cout << j+1 << ' ' << n << ' ' << 1 << ' ' << i-1 << ' ' << i << ' ' << j << endl;continue;}// b a ci = 1, j = n;while(p2[i-1] < sum && i <= n){i++;}while(s3[j+1] < sum && j >= 1){j--;}if(i <= j && p1[j]-p1[i-1] >= sum){cout << i << ' ' << j << ' ' << 1 << ' ' << i-1 << ' ' << j+1 << ' ' << n << endl;continue;}// c a bi = 1, j = n;while(p3[i-1] < sum && i <= n){i++;}while(s2[j+1] < sum && j >= 1){j--;}if(i <= j && p1[j]-p1[i-1] >= sum){cout << i << ' ' << j << ' ' << j+1 << ' ' << n << ' ' << 1 << ' ' << i-1 << endl;continue;}// c b ai = 1, j = n;while(p3[i-1] < sum && i <= n){i++;}while(s1[j+1] < sum && j >= 1){j--;}if(i <= j && p2[j]-p2[i-1] >= sum){cout << j+1 << ' ' << n << ' ' << i << ' ' << j << ' ' << 1 << ' ' << i-1 << endl;continue;}cout << -1 << endl;}return 0;
}D. Swap Dilemma


题意:就是说给你两个数组,然后每次再a数组选两个坐标,b数组选两个坐标,然后各自再各自的数组交换,然后问你最后两个数组能不能变成一样的
思路:这题我想到了两种做法
逆序对法
(1)逆序对的方法,众所周知,在大学有一门神奇的科目叫做线性代数,线性代数里面讲过一个东西叫做逆序对,只有逆序对的个数为同一奇偶性,才有可能相同,因为a,b数组每次都要变换一次,所以他们的奇偶性一定是都会在每一次变化,所以我们需要统计奇偶性,然后来判断,当然了,在之前还需要判断元素种类是否相同,如果个数不同一定为no
#include<bits/stdc++.h>
using namespace std;
#define int long long
int mergeSort(vector<int> &nums, int left, int right)
{if (left >= right) {return 0;}int mid = left + (right - left) / 2;int count = mergeSort(nums, left, mid) + mergeSort(nums, mid + 1, right);vector<int> tmp(right - left + 1);int i = left, j = mid + 1, k = 0;while (i <= mid && j <= right) {if (nums[i] <= nums[j]) {tmp[k++] = nums[i++];} else {tmp[k++] = nums[j++];count += mid - i + 1; // 计算逆序数}}while (i <= mid) {tmp[k++] = nums[i++];}while (j <= right) {tmp[k++] = nums[j++];}for (int p = 0; p < tmp.size(); ++p) {nums[left + p] = tmp[p];}return count;
}int solve(vector<int> &nums)
{if (nums.size() <= 1) {return 0;}return mergeSort(nums, 0, nums.size() - 1);
}void solve()
{map<int,int> mp;int n;cin >> n;vector<int> a(n+2);vector<int> b(n+2);for (int i=1;i<=n;i++) cin >> a[i];for (int i=1;i<=n;i++){cin >> b[i];mp[b[i]]=i;}for(int i=1;i<=n;i++){if(mp.count(a[i])==0){cout<<"NO\n";return ;}}int ans1=solve(a),ans2=solve(b);if (ans1%2 ==ans2%2) cout << "YES\n";else cout << "NO\n";
}
signed main()
{int t;cin >> t;while (t--) solve();return 0;
}交换次数法
(2)那么来讲另一种比较简单的方法,交换次数来判断,因为题目上所说每次两个数组都要交换,那么我们就只交换一个,然后统计变成另一个的次数为多少,是偶数就是yes是奇数就是no
当然了,在之前也是需要判断种类是否相同的
#include <bits/stdc++.h>
using namespace std;
#define int long long
int a[200005], b[200005];
map<int, int> mp;
void solve()
{mp.clear();int n;cin >> n;for (int i=1;i<=n;i++) cin >> a[i];for (int i=1;i<=n;i++){cin >> b[i];mp[b[i]]=i;}int ans = 0;for (int i=1;i<=n;i++){if (b[i] == a[i]) continue;if (mp.count(a[i]) == 0){cout << "NO\n";return;}int p=mp[a[i]];swap(b[i],b[p]);mp[b[i]]=i;mp[b[p]]=p;ans+=1; }if (ans%2 == 0) cout << "YES\n";else cout << "NO\n";
}
signed main()
{int t;cin >> t;while (t--) solve();return 0;
}相关文章:

Codeforces Round #956 (Div. 2) and ByteRace 2024(A~D题解)
这次比赛也是比较吃亏的,做题顺序出错了,先做的第三个,错在第三个数据点之后,才做的第二个(因为当时有个地方没检查出来)所以这次比赛还是一如既往地打拉了 那么就来发一下题解吧 A. Array Divisibility …...
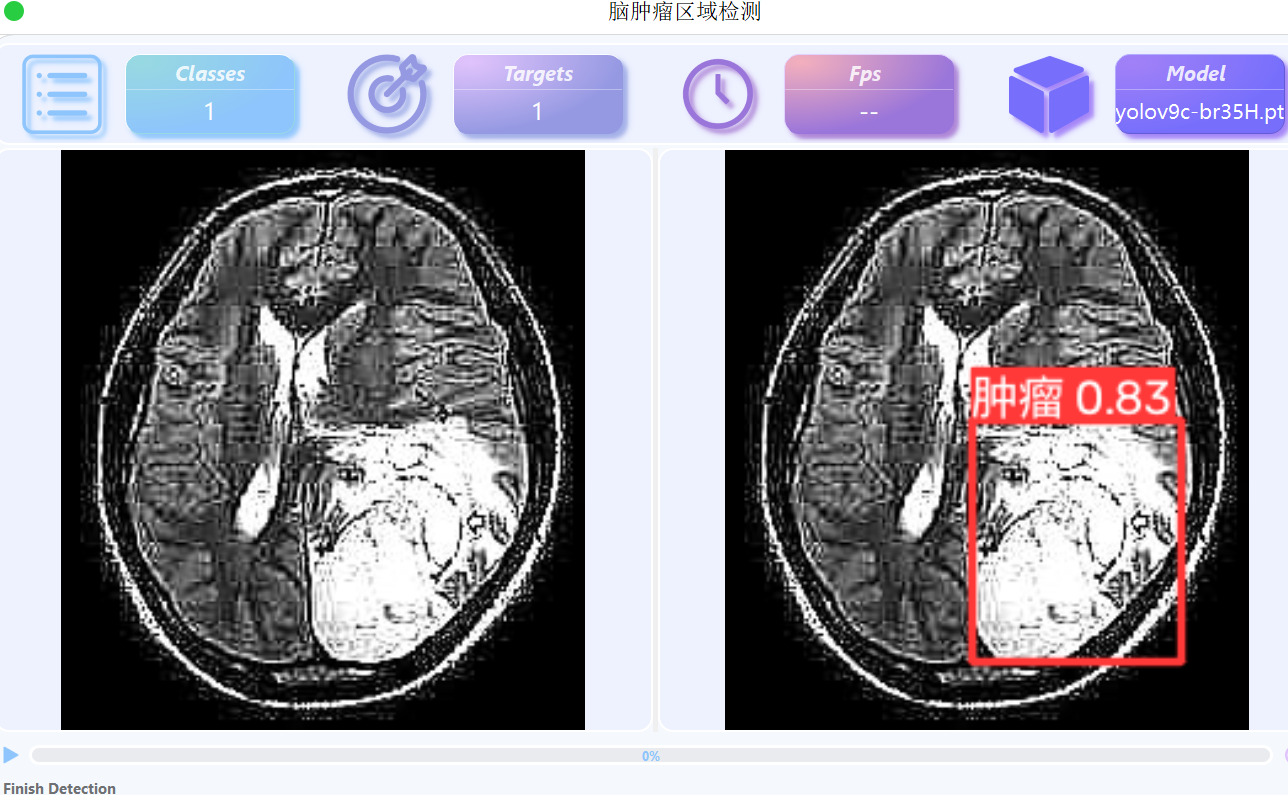
基于YOLOv9的脑肿瘤区域检测
数据集 脑肿瘤区域检测,我们直接采用kaggle公开数据集,Br35H 数据中已对医学图像中脑肿瘤位置进行标注 数据集我已经按照YOLO格式配置好,数据内容如下 数据集中共包含700张图像,其中训练集500张,验证集200张 模型训…...
阿里云 ECS 服务器的安全组设置
阿里云 ECS 服务器的安全组设置 缘由安全组多个安全组各司其职一些常见的IP段百度 IP 段华为云 IP 段搜狗蜘蛛 IP 段阿里云 IP 段 。。。 缘由 最近公司规模缩减,原有的托管在 IDC 机房的服务器,都被处理掉了,所有代码都迁移到了阿里云的云服…...

昇思25天学习打卡营第15天|应用实践之ShuffleNet图像分类
基本介绍 今天的应用实践的领域是计算机视觉领域,更确切的说是图像分类任务,不过,与昨日不同的是,今天所使用的模型是ShuffleNet模型。ShuffleNetV1是旷视科技提出的一种计算高效的CNN模型,和MobileNet, SqueezeNet等一…...

怀庄之醉适合搭配什么食物?
怀庄之醉作为一种独特的佳酿,其丰富的香气和层次感使其能够与多种食物搭配,提升餐饮体验。以下将具体探讨怀庄之醉适合搭配的食物类型,并分析为何这些搭配能够带来卓越的味觉享受。 一、肉类佳肴 怀庄之醉因其浓郁的口感,特别适…...

Java | Leetcode Java题解之第223题矩形面积
题目: 题解: class Solution {public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {int area1 (ax2 - ax1) * (ay2 - ay1), area2 (bx2 - bx1) * (by2 - by1);int overlapWidth Math.min(ax2, bx2) -…...

基于单片机的空调控制器的设计
摘 要 : 以单片机为核心的空调控制器因其体积小 、 成本低 、 功能强 、 简便易行而得到广泛应用 。 本设计通过 AT89S52 控制DS18&a…...

企业如何利用短视频平台做口碑塑造和品牌营销?
随着短视频平台的不断发展,新型的双微一抖小红书等新媒体平台,正在成为网民聚集的核心平台,小马识途营销顾问认为越来越多的企业应该利用这些平台进行品牌营销和宣传。其中,抖音和小红书作为短视频平台的代表,吸引了大…...

SQL INSERT批量插入方式
1、常规INSERT写法 INSERT INTO ... VALUES (...);INSERT INTO 表名( 字段1, 字段2) VALUES (字段1的值, 字段2的值);2、SELECT语句返回值INSERT INSERT INTO ...VALUES (..., (select ...));INSERT INTO 表名1(字段1, 字段2) VALUES (字段1的值, (select 查询字段 from 表名2 …...
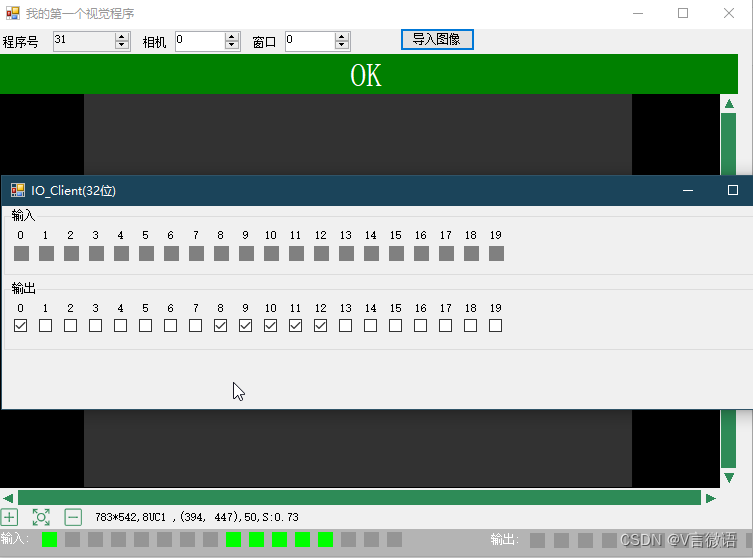
2.5 C#视觉程序开发实例1----IO_Manager实现切换程序
2.5 C#视觉程序开发实例1----IO_Manager实现切换程序 1 IO_Manager中输入实现 1.0 IO_Manager中输入部分引脚定义 // 设定index 目的是为了今后可以配置这些参数、 // 输入引脚定义 private int index_trig0 0; // trig index private int index_cst 7; //cst index priva…...
)
【入门篇】STM32寻址范围(更新中)
写在前面 STM32的寻址范围涉及存储器映射和32位地址线的使用。并且STM32的内存地址访问是按字节编址的,即每个存储单元是1字节(8位)。 一、寻址大小与范围 地址线根数 地址编号(二进制) 地址编号数(即内存大小) <...

DDD架构
1.DDD架构的概念: 领域驱动设计(Domain-Driven Design, DDD)是一种软件设计方法,旨在将软件系统的设计和开发焦点集中在领域模型上,以解决复杂业务问题 2.DDD架构解决了什么问题: 在以前的mvc架构种,三层结…...

Open3D KDtree的建立与使用
目录 一、概述 1.1kd树原理 1.2kd树搜索原理 1.3kd树构建示例 二、常见的领域搜索方式 2.1K近邻搜索(K-Nearest Neighbors, KNN Search) 2.2半径搜索(Radius Search) 2.3混合搜索(Hybrid Search) …...
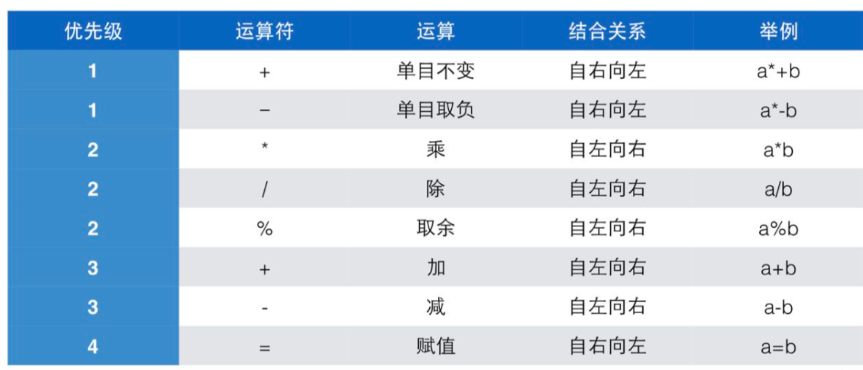
C语言编程3:运算符,运算符的基本用法
C语言3🔥:运算符,运算符的基本用法 一、运算符🌿 🎇1.1 定义 运算符是指进行运算的动作,比如加法运算符"“,减法运算符”-" 算子是指参与运算的值,这个值可能是常数&a…...

如何通过SPI机制去实现读取配置文件并动态加载对应实现类
最近写完鱼皮的RPC项目后,打算整理出来一些编程技巧的模版。 有两种实现:1.ServiceLoader 2.SpiLoader 一、直接使用java.util下的ServiceLoader 首先在resource目录下创建 META-INF/services 目录,并且创一个名称为对应要实现的接口的包…...

双链表(数组模拟)
双链表(数组模拟) 什么是双链表数组模拟双链表题目 什么是双链表 双链表不同于单链表的是 每一个节点不但存储了下一个节点的位置,也存储了上一个节点的位置。 数组模拟双链表 所以如果用数组的话,就需要创建三个数组。 题目 …...

ChatGPT 5.0:一年半后的展望与看法
在人工智能领域,每一次技术的飞跃都预示着未来生活与工作方式的深刻变革。随着OpenAI在人工智能领域的不断探索与突破,ChatGPT系列模型已成为全球关注的焦点。当谈及ChatGPT 5.0在未来一年半后可能发布的前景时,我们不禁充满期待,…...
城市地下综合管廊物联网远程监控
城市地下综合管廊物联网远程监控 城市地下综合管廊,作为现代都市基础设施的重要组成部分,其物联网远程监控系统的构建是实现智慧城市建设的关键环节。这一系统集成了先进的信息技术、传感器技术、通信技术和数据处理技术,旨在对埋设于地下的…...

VS 附加进程调试
背景: 此方式适合VS、代码和待调试的exe在同一台机器上。 一、还原代码到和正在跑的exe同版本 此操作可以保证能够调试生产环境的exe 二、设置符号路径 1.调试->选项 三、附加进程 方式1: 打开VS,调试->附加到进程,出…...

核函数的深入理解
核函数 (Kernel Function)是一种在高维特征空间中隐式计算内积的方法,它允许在原始低维空间中通过一个简单的函数来实现高维空间中的内积计算,而无需显式地计算高维特征向量。 核函数 的基本思想是通过一个映射函数 ϕ \phi ϕ …...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
