当前位置： 首页 > news >正文

JavaScript基础： JavaScript 数字类型

news 2026/2/8 20:18:17

JavaScript 中的数字类型是用来表示数值的数据类型。JavaScript 的数字类型是基于 IEEE 754 标准的双精度浮点数格式，这意味着它可以表示非常大和非常小的数值，以及小数。

数字字面量

在 JavaScript 中，数字可以直接以字面量的形式书写，例如：

let num1 = 123;       // 整数
let num2 = 123.456;   // 浮点数

科学计数法

JavaScript 也支持科学计数法，用于表示非常大或非常小的数字。科学计数法的形式是 aen，其中 a 是基数，e（或 E）表示“指数”，n 是指数的值。

例如，123e5 表示 123 乘以 10 的 5 次方：

let num3 = 123e5;     // 12300000

这等同于：

let num3 = 123 * 10 *10*10*10*10;  // 123 * 100000 = 12300000

同样，123e-5 表示 123 乘以 10 的 -5 次方：

let num4 = 123e-5; // 0.00123

示例：

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>JavaScript数字类型</title>
</head>
<body><p id="demo"></p>
<script>
document.getElementById("demo").innerHTML = 123e5;
</script></body>
</html>运行结果：12300000

特殊数值

JavaScript 数字类型还包括一些特殊的数值：

  • Infinity：表示正无穷大。
  • -Infinity：表示负无穷大。
  • NaN（Not-a-Number）：表示不是一个数字的值。

例如：

let inf = Infinity; // 正无穷大 
let negInf = -Infinity; // 负无穷大 
let notANumber = NaN; // 不是一个数字

数字方法和属性

JavaScript 的 Number 对象提供了一些方法和属性来处理数字：

  • Number.MAX_VALUE：表示 JavaScript 中可表示的最大数值。
  • Number.MIN_VALUE：表示 JavaScript 中可表示的最小正值。
  • Number.POSITIVE_INFINITY：表示正无穷大。
  • Number.NEGATIVE_INFINITY：表示负无穷大。
  • Number.NaN：表示不是一个数字。

例如：

console.log(Number.MAX_VALUE); // 输出 JavaScript 中可表示的最大数值console.log(Number.MIN_VALUE); // 输出 JavaScript 中可表示的最小正值

数字转换

JavaScript 提供了一些方法来将字符串或其他类型的值转换为数字：

  • Number()：将值转换为数字。
  • parseInt()：将字符串转换为整数。
  • parseFloat()：将字符串转换为浮点数。

例如：

let num5 = Number("123"); // 123 
let num6 = parseInt("123.45"); // 123 
let num7 = parseFloat("123.45"); // 123.45

总结

JavaScript 的数字类型非常灵活，可以表示整数、浮点数、科学计数法表示的数值，以及一些特殊的数值如 Infinity 和 NaN。通过 Number 对象提供的方法和属性，可以方便地进行数值处理和转换。

相关文章：

JavaScript基础： JavaScript 数字类型

JavaScript 中的数字类型是用来表示数值的数据类型。JavaScript 的数字类型是基于 IEEE 754 标准的双精度浮点数格式&#xff0c;这意味着它可以表示非常大和非常小的数值&#xff0c;以及小数。 数字字面量 在 JavaScript 中&#xff0c;数字可以直接以字面量的形式书写&…...

编程日记 2024/7/9 19:26:51

【网络安全】漏洞挖掘之Spring Cloud注入漏洞

漏洞描述 Spring框架为现代基于java的企业应用程序(在任何类型的部署平台上)提供了一个全面的编程和配置模型。 Spring Cloud 中的 serveless框架 Spring Cloud Function 中的 RoutingFunction 类的 apply 方法将请求头中的“spring.cloud.function.routing-expression”参数…...

编程日记 2024/7/9 19:24:49

面试官：MySQL死锁是什么，如何解决？

MySQL死锁概述 定义&#xff1a;多个操作相互等待对方释放资源&#xff0c;导致无法继续执行的情况。场景&#xff1a;通常发生在多个事务同时试图锁定对方已锁定的资源时。 MySQL锁的分类 粒度分类&#xff1a; 表级锁&#xff1a;锁定整个表&#xff0c;简单但并发能力低。…...

编程日记 2024/7/9 19:22:46

CSS原子化

目录 一、定义 二、原子化工具 2.1、tailwind 2.1.1、以PostCss插件形式安装 2.1.2、不依赖PostCss安装 2.1.3、修改原始配置 2.2、unocss 三、优缺点 3.1、优点 3.2、缺点 一、定义 定义&#xff1a;使用一系列的助记词&#xff0c;利用类名来代表样式。 二、原子化…...

编程日记 2024/7/9 19:21:45

【Python的pip配置、程序运行、生成exe文件】

Python的pip配置、程序运行、生成exe文件 一、安装Python 通过官网下载对应的版本&#xff0c;安装即可。 下载地址&#xff1a;https://www.python.org/downloads/ Python标准库查看&#xff08;Python自带库&#xff09; Python 标准库文档 安装Python的时候&#xff0c…...

编程日记 2024/7/9 19:19:44

神经网络习题

不具有权重共享的网络是&#xff1a; **多层感知机&#xff08;Multilayer Perceptron&#xff0c;MLP&#xff09;&#xff1a; ** 特点&#xff1a;每一层的每一个神经元都与上一层的每一个神经元全连接&#xff0c;权重独立于每个连接&#xff0c;不存在权重共享。 权重共享…...

编程日记 2024/7/9 19:18:43

deepstream段错误

&#x1f610; 错误&#xff1a; 探针中由于使用了pyds.get_nvds_buf_surface(hash(gst_buffer), frame_meta.batch_id)导致的段错误&#xff08;segmentation fault&#xff09;。 解决方式&#xff1a;...

编程日记 2024/7/9 19:15:40

《梦醒蝶飞：释放Excel函数与公式的力量》10.1.1函数简介

10.1.1函数简介 BIN2DEC函数是Excel中用于将二进制数转换为十进制数的函数。它在处理二进制数时非常有用&#xff0c;尤其是在电子工程、计算机科学等领域。 10.1.2函数语法&#xff1a; BIN2DEC(number) number&#xff1a;这是要转换的二进制数&#xff0c;必须是以字符串…...

编程日记 2024/7/9 19:13:38

Bert 变种， T5模型

NLP-预训练模型-2019-NLU&#xff1a;DistilBERT【 BERT模型压缩】【模型大小减小了40%&#xff08;66M&#xff09;&#xff0c;推断速度提升了60%&#xff0c;但性能只降低了约3%】_distillbert-CSDN博客 https://zhuanlan.zhihu.com/p/673535548 大语言模型系列-T5_t5模型…...

编程日记 2024/7/9 19:12:37

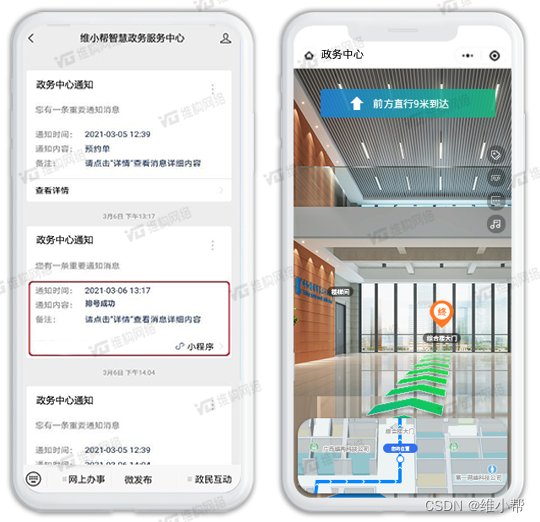
技术赋能政务服务：VR导视与AI客服在政务大厅的创新应用

在数字化转型的浪潮中&#xff0c;政务大厅作为服务民众的前沿阵地&#xff0c;其服务效率和质量直接影响着政府形象和民众满意度。然而&#xff0c;许多政务大厅仍面临着缺乏智能化导航系统的挑战&#xff0c;这不仅增加了群众的办事难度&#xff0c;也降低了服务效率。维小帮…...

编程日记 2024/7/9 19:11:36

大模型备案全网最详细流程【附附件】

本文要点&#xff1a;大模型备案最详细说明&#xff0c;大模型备案条件有哪些&#xff0c;《算法安全自评估报告》模板&#xff0c;大模型算法备案&#xff0c;大模型上线备案&#xff0c;生成式人工智能(大语言模型)安全评估要点&#xff0c;网信办大模型备案。 大模型备案安…...

编程日记 2024/7/9 19:10:35

0090__【Git系列】merge和rebase的区别

【Git系列】merge和rebase的区别_rebase和merge的区别-CSDN博客 git中rebase和merge的区别是什么-git-PHP中文网 https://blog.51cto.com/qzcsbj/9444199...

编程日记 2024/7/9 19:09:34

谈面向任务的多轮对话系统（TOD）

面向任务对话系统&#xff08;Task-Oriented Dialogue (TOD) Systems)主要是为解决特定任务的&#xff0c;比如订票任务&#xff08;订机票&#xff0c;电影票等&#xff09;&#xff0c;预定饭店等。这种对话往往需要多轮对话才能够完成。 多轮对话的例子 客户预定一个餐厅的…...

编程日记 2024/7/9 19:08:33

汇凯金业：如何判断黄金的买入时机

黄金&#xff0c;作为全球公认的避险资产&#xff0c;其价格波动受到多种因素的影响&#xff0c;包括经济数据、货币政策、地缘政治风险等。对于投资者而言&#xff0c;把握黄金的最佳买入点是实现投资收益最大化的关键。本文将探讨影响黄金价格的主要因素&#xff0c;并提供一…...

编程日记 2024/7/9 19:07:32

tomcat 项目迁移，无法将项目作为服务service启动

背景 测试服务器需要迁移到正式服务器上&#xff0c;为了方便省事&#xff0c;将测试服务器上的一些文件直接复制到正式服务器 问题 使用startup启动项目之后&#xff0c;可以直接使用使用tomcat9w启动&#xff0c;或者作为服务service启动的时候&#xff0c;显示无法访问到资源…...

编程日记 2024/7/9 19:06:31

java中 使用数组实现需求小案例（二）

Date: 2024.07.09 16:43:47 author: lijianzhan 需求实现&#xff1a; 设计一个java类&#xff0c;java方法&#xff0c;使用Random函数&#xff0c;根据实现用户输入随机数生成一个打乱的数组。 package com.lin.java.test;import java.util.Arrays; import java.util.Rando…...

编程日记 2024/7/9 19:04:28

【删库跑路】一次删除pip下载的所有第三方库方法

进入命令行&#xff0c;先list看下库存 pip list导出所有的第三方库至一文件列表 pip freeze >requirements.txt按照列表卸载所有库 pip uninstall -r requirements.txt -y再list看下&#xff0c;可见库存已清空...

编程日记 2024/7/9 19:03:27

Java面试八股之MySQL索引B+树、全文索引、哈希索引

MySQL索引B树、全文索引、哈希索引 注意&#xff1a;B树中B不是代表二叉树&#xff08;binary&#xff09;&#xff0c;而是代表平衡&#xff08;balance&#xff09;&#xff0c;因为B树是从最早的平衡二叉树演化而来&#xff0c;但是B树不是一个二叉树。 B树的高度一般在2~…...

编程日记 2024/7/9 19:02:25

解决 Docker 容器镜像拉取难题：全面指南

一、引言 在使用 Docker 容器的过程中&#xff0c;经常会遇到镜像拉取慢甚至无法下载的问题&#xff0c;这给开发和部署工作带来了不小的困扰。本文将深入探讨这一问题的原因&#xff0c;并提供多种有效的解决方案。 二、问题原因分析 网络限制 本地网络带宽不足或存在网络拥…...

编程日记 2024/7/9 19:01:24

python基础语法笔记（有C语言基础之后）

input()用于输入&#xff0c;其有返回值&#xff08;即用户输入的值&#xff09;&#xff0c;默认返回字符串。括号里可放提示语句 一行代码若想分为多行来写&#xff0c;需要在每一行的末尾加上“\” 单个“/”表示数学中的除法&#xff0c;不会取整。“//”才会向下取整。 …...

编程日记 2024/7/9 19:00:23

基于算法竞赛的c++编程（28）结构体的进阶应用

结构体的嵌套与复杂数据组织 在C中&#xff0c;结构体可以嵌套使用&#xff0c;形成更复杂的数据结构。例如&#xff0c;可以通过嵌套结构体描述多层级数据关系&#xff1a; struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

编程新知 2025/11/16 19:06:23

未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？

编辑&#xff1a;陈萍萍的公主一点人工一点智能 未来机器人的大脑&#xff1a;如何用神经网络模拟器实现更智能的决策&#xff1f;RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战&#xff0c;在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

编程新知 2026/2/7 23:18:28

以下是对华为 HarmonyOS NETX 5属性动画（ArkTS）文档的结构化整理，通过层级标题、表格和代码块提升可读性：

一、属性动画概述NETX 作用&#xff1a;实现组件通用属性的渐变过渡效果&#xff0c;提升用户体验。支持属性&#xff1a;width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项&#xff1a; 布局类属性&#xff08;如宽高&#xff09;变化时&#…...

编程新知 2026/1/28 21:15:38

线程同步：确保多线程程序的安全与高效！

全文目录&#xff1a; 开篇语前序前言第一部分&#xff1a;线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分&#xff1a;synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分&#xff…...

编程新知 2025/9/24 16:02:40

关于nvm与node.js

1 安装nvm 安装过程中手动修改 nvm的安装路径&#xff0c; 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解&#xff0c;但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后&#xff0c;通常在该文件中会出现以下配置&…...

编程新知 2026/1/28 15:17:32

04-初识css

一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

编程新知 2026/1/29 17:54:05

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控，故障处理工具

第2章 虚拟机性能监控&#xff0c;故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令&#xff1a;jps [options] [hostid] 功能&#xff1a;本地虚拟机进程显示进程ID&#xff08;与ps相同&#xff09;&#xff0c;可同时显示主类&#x…...

编程新知 2026/1/15 1:34:10

JVM暂停（Stop-The-World，STW）的原因分类及对应排查方案

JVM暂停（Stop-The-World，STW）的完整原因分类及对应排查方案，结合JVM运行机制和常见故障场景整理而成： 一、GC相关暂停​​ 1. ​​安全点（Safepoint）阻塞​​ ​​现象​​：JVM暂停但无GC日志，日志显示No GCs detected。​​原因​​：JVM等待所有线程进入安全点（如…...

编程新知 2026/2/7 11:25:15

Java多线程实现之Thread类深度解析

Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

编程新知 2025/8/28 21:52:02

HDFS分布式存储 zookeeper

hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架&#xff0c;允许使用简单的变成模型跨计算机对大型集群进行分布式处理&#xff08;1.海量的数据存储 2.海量数据的计算&#xff09;Hadoop核心组件 hdfs&#xff08;分布式文件存储系统&#xff09;&a…...

编程新知 2026/1/24 4:10:44