大话光学原理:2.最短时间原理、“魔法石”与彩虹
一、最短时间原理
1662年左右,费马在一张信纸的边角,用他那著名的潦草笔迹,随意地写下了一行字:“光在两点间选择的路,总是耗时最少的。”这句话,简单而深邃,像是一颗悄然种下的种子,准备在学界的土壤中生根发芽,这便是后来闻名遐迩的“费马最短时间原理”。仿佛他还在低语:“可惜这空白太小,写不下更多了。”这位伟大的数学家,又一次轻轻挑动了学术界的敏感神经。
这“耗时最短”,实际上意味着光跑得最快。速度和角度,两个看似毫不相干的物理概念,却通过费马原理神奇地交织在一起,揭示了自然界的奥秘。按照斯涅耳定律,光在穿越不同介质时,只需遵循既定的折射率,灵活调整方向,便能在各种介质间穿梭自如。这一过程,似乎与我们所理解的因果律完美契合。
但费马的最短时间原理,却像一块巨石砸入平静的湖面,激起了层层涟漪。如果每一道光都必须计算时间损耗,那么在出发前,它是如何预知自己的去向,以及途中将面临的种种变数呢?从A点到B点,它可以径直前行,也可以像醉酒的人一样曲折摇摆,甚至有可能绕个大圈子后再返回原点。即使知道最终的归宿,光又该如何选择一条最优的路径呢?这些问题,让人们对这个原理充满了好奇和探索的欲望。

想象一下,你是那束勇敢的光,肩负着从A点到B点的旅程。在这个遵循时空王国最新发布的“最短时间章程”的宇宙中,你不仅需要知道终点B的确切坐标,更要详尽了解路途中的每一个转折——哪些界面会遇见,它们的位置在哪里,以及你将穿越的种种介质。只有掌握了这些细节,你才能绘制出一条效率最高的路径。否则,盲目出发的你,可能会在一个未知的界面面前措手不及,不得不在现场临时调整方向,这样的曲折,无疑会增加你的旅行时间。
在“费马章程”的指导下,光在起跑线上时就必须对所有可能的路径了如指掌,预先规划好最佳路线。仿佛是先知道旅行的终点,然后再反向规划整个行程,这就像是逆着时间行进的一场盛大游行,将“先后”、“因果”的逻辑顺序彻底颠覆。
但随着实验技术的进步,学者们发现费马对光行为的理解还不够完整。光不仅仅选择光程最短的路径,有时候它会选择一个固定的路径,甚至是在某些特殊情况下,会选择一条光程最大的路径。这需要一定的技巧,像是引导光去完成一场欺骗游戏——例如,将光源放在椭圆的一个焦点上,然后在椭圆内壁安装抛物镜,这样光线就会落在抛物镜的底端。于是,费马原理更精确的表述应该是:光总是选择使得光程的一阶变分为零的路径,连接两个点A和B。
随着人类对宇宙认知的加深,最短时间原理演变成了更为全面的“最小作用量原理”,并在广义相对论、量子场论等现代物理领域发挥着重要作用。对于光来说,它那奇妙的旅行规律,只是它带给人类众多知识盛宴中的一道开胃菜。在觥筹交错的学术探讨中,一场从古典力学到量子力学的思维盛宴正在缓缓展开。
二、“魔法石”与彩虹
正当费马初试啼声之际,一位四处游学的年轻学士恰好漫游至罗马。他带着一颗神奇的石头,向同行的亚里士多德学派学者们炫耀。这石头看似平凡无奇,表面粗糙且色泽黯淡,就像一块普通的石片。然而,当年轻人把它置于阳光下曝晒一番,随后引领众人进入一间漆黑的暗室时,奇迹发生了:在黑暗中,那石头仿佛被霞光轻抚,自发地散出温柔的荧光,仿佛将阳光本身拘禁于其内,带入这幽暗的空间。
这位充满机智的年轻人就是伽利略,而他手中的石块学名为硫化钡。博洛尼亚的炼金术士们曾赋予它一个充满诗意的名字:“太阳海绵”。我们现在明白,硫化物晶体的发光,是因为其分子在热辐射的激发下释放出了能量。

在探索光之奥秘的征途上,伽利略虽对“太阳海绵”的发光原理一头雾水,但那幽暗中温柔的光辉却激发了他敏锐的直觉。他成了自希腊时代落幕以来,首位对光的本质提出新解的科学家。伽利略大胆推测,光并非单一的存在,而是由无数不可见的微小颗粒组成,就像水珠或沙粒一样。这些颗粒构成了光的实体,它们可以被测量,也能与其他物质互动:碰撞、反弹、渗透……光不再依赖于任何超自然的力量,就可以从一个地方传递到另一个地方。
这一新观点打破了古老观念的束缚,挑战了发光物体与普通物体之间的界限,同时也颠覆了将光视为虚无附庸的传统看法。尽管惹恼了保守的长老们,想要扼杀这新思想的嫩芽,但在那岩石碎片中闪耀的柔和光芒面前,他们的怒吼显得微不足道。
太阳海绵成为了揭示“光是由微粒组成”这一理论的突破口。伽利略为了追寻真理,不畏艰难,勇敢地走向已知与未知的边缘。
到了17世纪末,物理学作为一门独立学科逐渐崛起,艾萨克·牛顿作为伽利略的杰出继承者,为微粒说提供了有力的证据。他利用精心制作的三棱镜,将白光拆解成一条绚丽的色彩带:红、橙、黄、绿、蓝、靛、紫,这不就是天空中彩虹的颜色吗?

通过扩展费马原理,我们明白了棱镜是如何分解白光的。光在真空中速度一致,但进入介质后速度各异,导致不同颜色光的折射率不同。白光穿过透镜时,经历了两次转向,每种颜色的光都遵循自己的折射率偏转,直至七种颜色完全分离。这个过程,就像是将一群不同性格的单色光颗粒分拣出来,让它们各自归队。
光仿佛在感叹:原来“我”并非单独存在,而是“我们”。当光的队列重新排列,即使是透明的光芒也能在天空中绘出一道绚丽的彩虹。
相关文章:

大话光学原理:2.最短时间原理、“魔法石”与彩虹
一、最短时间原理 1662年左右,费马在一张信纸的边角,用他那著名的潦草笔迹,随意地写下了一行字:“光在两点间选择的路,总是耗时最少的。”这句话,简单而深邃,像是一颗悄然种下的种子,…...

spring tx @Transactional 详解 `Advisor`、`Target`、`ProxyFactory
在Spring中,Transactional注解的处理涉及到多个关键组件,包括Advisor、Target、ProxyFactory等。下面是详细的解析和代码示例,解释这些组件是如何协同工作的。 1. 关键组件介绍 1.1 Advisor Advisor是一个Spring AOP的概念,它包…...
)
`CyclicBarrier` 是 Java 中的一个同步辅助工具类,它允许一组线程相互等待,直到所有线程都达到了某个公共屏障点(barrier point)
CyclicBarrier 是 Java 中的一个同步辅助工具类,它允许一组线程相互等待,直到所有线程都达到了某个公共屏障点(barrier point)。当所有线程都到达屏障点时,它们可以继续执行后续操作。CyclicBarrier 的特点是可以重复使…...

华为机试HJ108求最小公倍数
华为机试HJ108求最小公倍数 题目: 想法: 要找到输入的两个数的最小公倍数,这个最小公倍数要大于等于其中最大的那个数值,遍历最大的那个数值的倍数,最大的最小公倍数就是输入的两个数值的乘积 input_number_list i…...
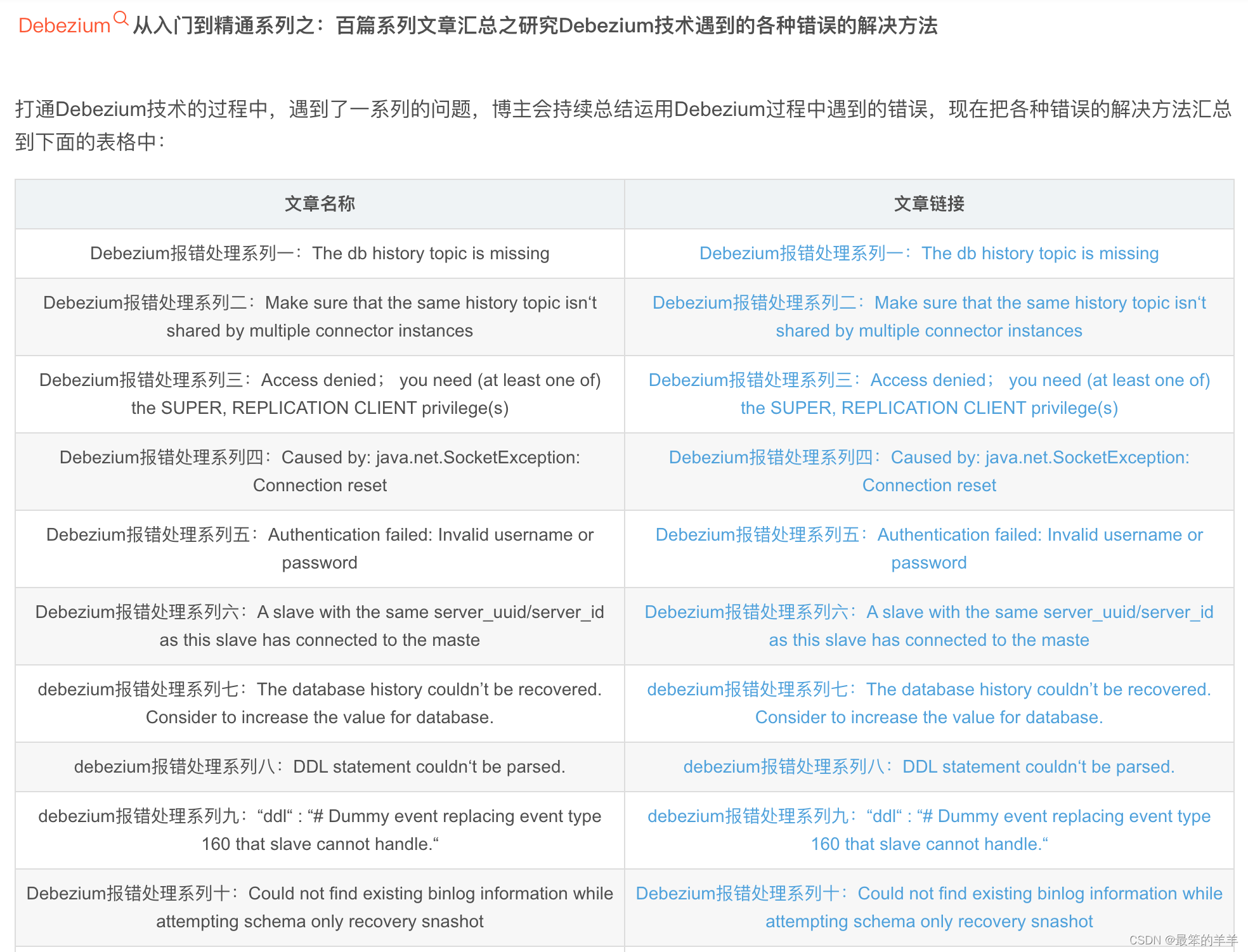
Debezium报错处理系列之第114篇:No TableMapEventData has been found for table id:256.
Debezium报错处理系列之第114篇:Caused by: com.github.shyiko.mysql.binlog.event.deserialization.MissingTableMapEventException: No TableMapEventData has been found for table id:256. Usually that means that you have started reading binary log within the logic…...

开发者必看:MySQL主从复制与Laravel读写分离的完美搭配
介绍 主从同步配置的主要性不用多说,本文将详细介绍了如何在MySQL数据库中设置主从复制,以及如何在Laravel框架中实现数据库的读写分离。 通过一系列的步骤,包括修改MySQL配置、创建同步账户、获取二进制日志文件名和位置、导出主服务器数据…...

二战架构师,拿下
前言 已经许久更新文章了,并不是因为我懒了,而是在备考系统架构师考试。个人感觉还是比较幸运的,低分飘过。现阶段任务也算完成了,记录一下感受。 什么是软考 软考,全称“计算机技术与软件专业技术资格(…...

泛微开发修炼之旅--35关于基于页面扩展和自定义按钮实现与后端交互调用的方法
文章链接:35关于基于页面扩展和自定义按钮实现与后端交互调用的方法...
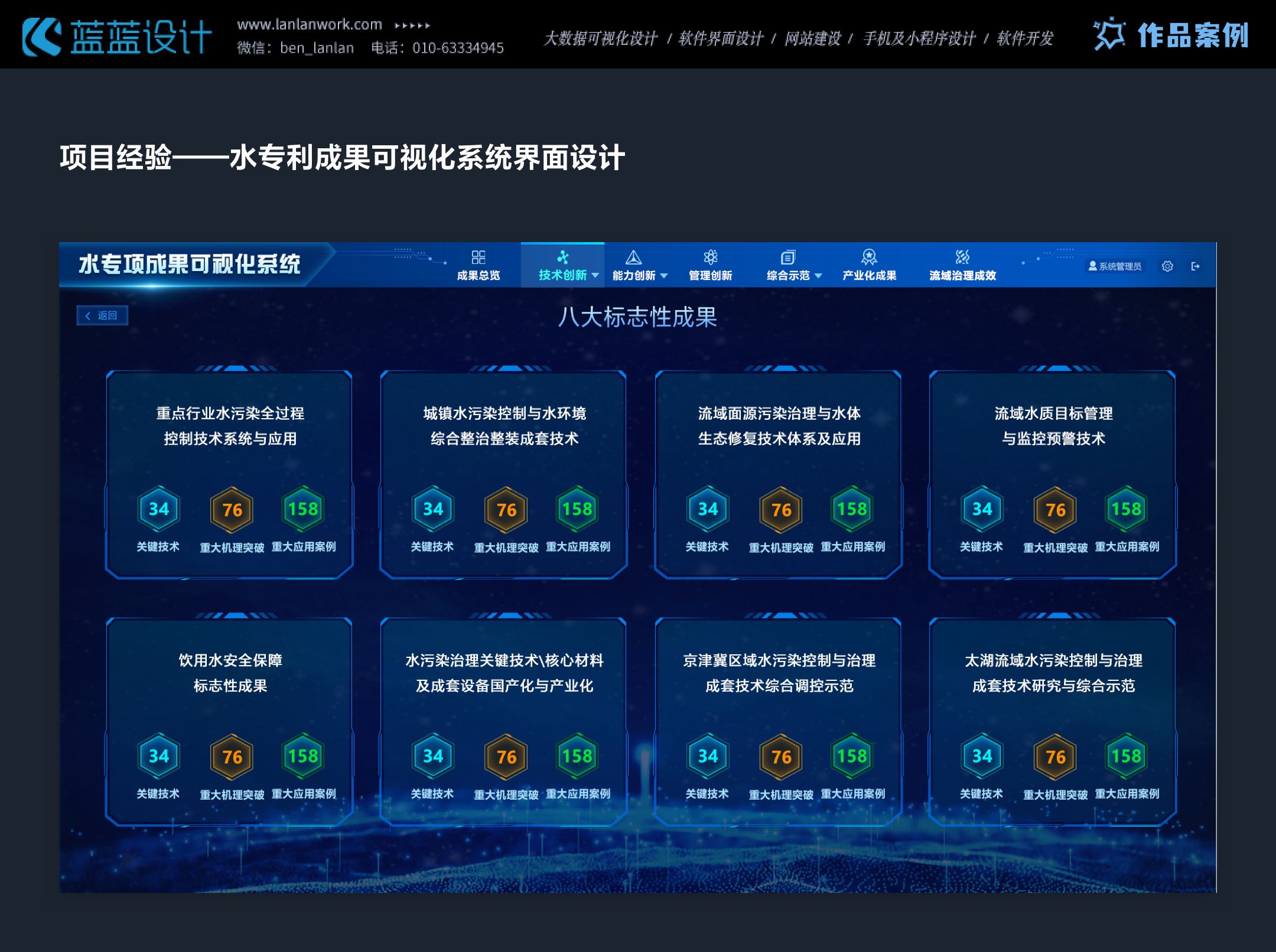
原创作品—数据可视化大屏
设计数据可视化大屏时,用户体验方面需注重以下几点:首先,确保大屏信息层次分明,主要数据突出显示,次要信息适当弱化,帮助用户快速捕捉关键信息。其次,设计应直观易懂,避免复杂难懂的…...
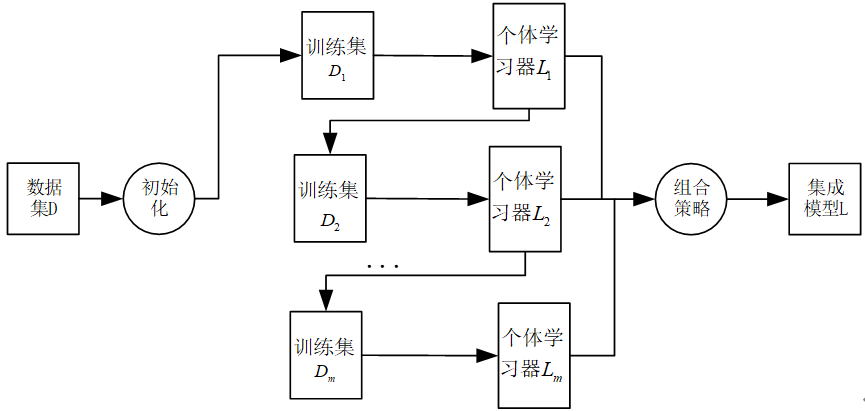
AdaBoost集成学习算法理论解读以及公式为什么这么设计?
本文致力于阐述AdaBoost基本步骤涉及的每一个公式和公式为什么这么设计。 AdaBoost集成学习算法基本上遵从Boosting集成学习思想,通过不断迭代更新训练样本集的样本权重分布获得一组性能互补的弱学习器,然后通过加权投票等方式将这些弱学习器集成起来得到…...

uniapp内置组件uni.navigateTo跳转后页面空白问题解决
文章目录 导文空白问题 导文 在h5上跳转正常 但是在小程序里面跳转有问题 无任何报错 页面跳转地址显示正确,但页面内容为空 空白问题 控制台: 问题解决: 方法1: 可能是没有注册的问题,把没注册的页面 注册一下。 方…...

使用树莓派进行python开发,控制电机的参考资料
网站连接:https://www.cnblogs.com/kevenduan?page1 1、简洁的过程步骤, 2、有代码示例, 3、有注意事项,...

protobuf的使用
protobuf:是一种数据格式,独立于平台,独立于语言,是一种二进制格式,可以存储更加复杂的数据结构,比如图,树,结构体,类 作用: 1.持久化:把数据存…...

笔记15:while语句编程练习
练习一: 编写程序,求 2^24^26^2...n^2? -直到累加和大于或等于 10000 为止,输出累加和 -输出累加式中的项数,以及最大的数 n #include<stdio.h> int main() {int sum 0;int i 1;int n 0;while(sum < 10000)//将sum…...

打开excel时弹出stdole32.tlb
问题描述 打开excel时弹出stdole32.tlb 如下图: 解决方法 打开 Microsoft Excel 并收到关于 stdole32.tlb 的错误提示时,通常意味着与 Excel 相关的某个组件或类型库可能已损坏或不兼容。 stdole32.tlb 是一个用于存储自动化对象定义的类型库&#x…...

349. 两个数组的交集
哈喽!大家好,我是奇哥,一位专门给面试官添堵的职业面试员 文章持续更新,可以微信搜索【小奇JAVA面试】第一时间阅读,回复【资料】更有我为大家准备的福利哟! 文章目录 一、题目二、答案三、总结 一、题目 …...

重庆交通大学数学与统计学院携手泰迪智能科技共建的“智能工作室”
2024年7月4日,重庆交通大学数学与统计学院与广东泰迪智能科技股份有限公司携手共建的“智能工作室”授牌仪式在南岸校区阳光会议室举行。此举标志着数统学院与广东泰迪公司校企合作新篇章的开启,也预示着学院在智能科技教育领域的深入探索和实践。 广东…...

Pandas在生物信息学中的应用详解
Pandas在生物信息学中的应用详解 引言 生物信息学作为一门将计算机科学和生物学相结合的跨学科领域,正随着高通量实验技术的飞速发展而日益重要。Pandas,作为Python中一个强大的数据处理库,为生物信息学研究提供了便捷高效的数据处理和分析…...

ByteMD富文本编辑器的vue3配置
Git地址:GitHub - bytedance/bytemd: ByteMD v1 repository 控制面板输入 npm install bytemd/vue-next 下载成功后在src/main.ts中引用 import "bytemd/dist/index.css";引入后保存,下面是一些插件,比如说我用到gmf和hightLight&…...

基于antdesign封装一个react的上传组件
项目中遇到了一个上传的需求,看了一下已有的代码很粗糙,而且是直接引用andt的组件,体验不太好,自己使用FormData对象封装了一个上传组件,仅供参考。 代码如下: /*** FileUploadModal* description - 文件选…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
