概论(二)随机变量
1.名词解释
1.1 样本空间
一次具体实验中所有可能出现的结果,构成一个样本空间。
1.2 随机变量
把结果抽象成数值,结果和数值的对应关系就形成了随机变量X。例如把抛一次硬币的结果,正面记为1,反面记为0。有变量相对应的就有自变量,此处我们不用Y而是用P(X)来表示,P(X)就是X取某值时的概率。
1.3 结果轴
随机变量X作为结果是均匀分布在x轴上的,有的是x轴上某一段,甚至只是x轴上的两个点,例如抛硬币只有两种结果,所以对应在x轴上只有两个点x=1或x=0。有的结果可以遍布整个x轴。
误区:在写这段的时候莫名地把正态分布认为是标准正太分布,想到人的身高是符合正太分布的,但又考虑到人的身高不可能有负数,所以大脑就迷糊了。
1.4 概率密度函数PMF
结果是在x轴上均匀分布的,但是每次实验取得结果的可能性却不一定相同,拿离散变量中连续抛两次硬币的结果统计,显然
| 第一次正 | 第一次反 | |
|---|---|---|
| 第二次正 | 1/4 | 1/4 |
| 第二次反 | 1/4 | 1/4 |
所以一正一反的概率为1/2,X取不同值P(X)随之相应变化,这就构成了概率函数,为什么叫概率密度函数呢?我门可以想象一条由无数个密度不同的铁点焊接成的铁丝,我们任选铁丝其中一点这就类似于随机变量X的取值,该点的密度就类似于概率P(X)
2.常见分布
2.1 常见离散分布
离散分布的概率计算是有限种结果的概率累加
P ( X ∣ X ≤ x n ) = ∑ i = 1 n P ( x i ) P(X|X\le x_n)=\sum_{i=1}^{n}P(x_i) P(X∣X≤xn)=i=1∑nP(xi)
2.1.1 二项分布
2.1.2 几何分布
2.1.3 泊松分布
泊松分布是n很大,p很小的二项分布的近似,其中 λ = n p \lambda=np λ=np
2.2 常见连续分布
连续分布无法通过直接累加进行计算,因为其包含无数种可能,所以我们利用积分的形式进行计算。
2.2.1 均匀分布
2.2.2 指数分布
2.2.3正态分布(高斯分布)
- 一元高斯分布
- 多元高斯分布
X X X有多个维度 x 1 , x 2 , . . . x p x_1,x_2,...x_p x1,x2,...xp而 X X X可以有n个,所以构成了n*p的矩阵
X = [ x 11 x 12 x 13 . . . x 1 p x 21 x 22 x 23 . . . x 2 p . . . . . . . . . . . . x n 1 x n 2 x n 3 . . . x n p ] X=\begin{bmatrix} x_{11}&x_{12}&x_{13}&...x_{1p}\\ x_{21}&x_{22}&x_{23}&...x_{2p}\\ ...&...&...&...\\ x_{n1}&x_{n2}&x_{n3}&...x_{np} \end{bmatrix} X= x11x21...xn1x12x22...xn2x13x23...xn3...x1p...x2p......xnp
对比一元高斯矩阵期望 μ 4 \mu4 μ4%此时的 μ = [ μ 1 μ 1 2 . . . u n ] \mu=\begin{bmatrix} \mu_1\\\mu_12\\...\\u_n \end{bmatrix} μ= μ1μ12...un ,是一个向量。
对比一元高斯矩阵的方差 σ 2 \sigma^2 σ2,多元高斯分布的是协方差矩阵,同样是一个对称矩阵
∑ = [ σ 11 σ 12 σ 13 . . . σ 1 p σ 21 σ 22 σ 23 . . . σ 2 p . . . . . . . . . . . . σ p 1 σ p 2 σ p 3 . . . σ p p ] \sum = \begin{bmatrix} \sigma_{11}&\sigma_{12}&\sigma_{13}&...\sigma_{1p}\\ \sigma_{21}&\sigma_{22}&\sigma_{23}&...\sigma_{2p}\\ ...&...&...&...\\ \sigma_{p1}&\sigma_{p2}&\sigma_{p3}&...\sigma_{pp} \end{bmatrix} ∑= σ11σ21...σp1σ12σ22...σp2σ13σ23...σp3...σ1p...σ2p......σpp
概率密度函数
p ( x ∣ θ ) = 1 ( 2 π ) p 2 ∣ Σ ∣ 1 2 e x p [ − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ] p(x|\theta)=\frac{1}{(2 \pi)^{\frac{p}{2}}|\Sigma |^{\frac{1}{2}}}exp[-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)] p(x∣θ)=(2π)2p∣Σ∣211exp[−21(x−μ)TΣ−1(x−μ)]
3. 二维分布
随机变量X和Y, P ( X = x i , Y = y i ) P(X=x_i,Y=y_i) P(X=xi,Y=yi)表示两件事同时发生概率,又称联合分布概率, P ( X = x i ∣ Y = y i ) P(X=x_i|Y=y_i) P(X=xi∣Y=yi)表示Y=y发生的条件下X=x的发生概率,又称条件概率。 P ( X = x i ) P(X=x_i) P(X=xi)成为边缘分布概率。
条件分布 = 联合分布 边缘分布 条件分布=\frac{联合分布}{边缘分布} 条件分布=边缘分布联合分布
得明白一个事情,就是如果X与Y没有交集那么对于二维分布来说就没有太多讨论的意义,因为两者的条件分布和联合分布概率都为0,边缘分布就是内部 P ( X = x i ) 或 ( Y = y i ) P(X=x_i)或(Y=y_i) P(X=xi)或(Y=yi)

Q1:如果X和Y有交集,那 P ( X = x 5 , Y = y 5 ) P(X=x_5,Y=y_5) P(X=x5,Y=y5)等于 P ( X = x 5 ∣ Y = y 5 ) P(X=x_5|Y=y_5) P(X=x5∣Y=y5)吗?
P ( X = x 5 , Y = y 5 ) P(X=x_5,Y=y_5) P(X=x5,Y=y5)的样本空间大小是55=25个,而 P ( X = x 5 ∣ Y = y 5 ) P(X=x_5|Y=y_5) P(X=x5∣Y=y5)的样本空间大小是51=5个

3.2 独立与相关
独立不代表两者不相容,两者不相容也不能证明两者独立
独立一定不相关,不独立一定相关,相关不一定不独立
X与Y独立,分别从离散和连续两个方面请证明:
E ( X + Y ) = E X + E Y E(X+Y)=EX+EY E(X+Y)=EX+EY
E ( X Y ) = E ( X ) E ( Y ) E(XY)=E(X)E(Y) E(XY)=E(X)E(Y)
V ( X + Y ) = V ( X ) + V ( Y ) V(X+Y)=V(X)+V(Y) V(X+Y)=V(X)+V(Y)
3.3 协方差
方差:
V [ X ] = E [ ( X − E [ X ] ) 2 ] = E [ X 2 − 2 X E [ X ] + ( E [ X ] ) 2 ] = E [ X 2 ] − 2 ( E [ X ] ) 2 + ( E [ X ] ) 2 = E [ X 2 ] − ( E [ X ] ) 2 V[X]=E[(X-E[X])^2]=E[X^2-2XE[X]+(E[X])^2]=E[X^2]-2(E[X])^2+(E[X])^2=E[X^2]-(E[X])^2 V[X]=E[(X−E[X])2]=E[X2−2XE[X]+(E[X])2]=E[X2]−2(E[X])2+(E[X])2=E[X2]−(E[X])2
协方差:
c o v ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] cov(X,Y)=E[(X-E(X))(Y-E(Y))] cov(X,Y)=E[(X−E(X))(Y−E(Y))]
体会两者的不同
3.4 协方差矩阵
如果随机变量的个数提高到n个,则需要单独计算每个变量之间的协方差,同样也需要计算自己与自己的协方差,根据公式可知自己与自己的协方差就是方差,如此我们就构建了一个对称矩阵,称为协方差矩阵。
相关文章:

概论(二)随机变量
1.名词解释 1.1 样本空间 一次具体实验中所有可能出现的结果,构成一个样本空间。 1.2 随机变量 把结果抽象成数值,结果和数值的对应关系就形成了随机变量X。例如把抛一次硬币的结果,正面记为1,反面记为0。有变量相对应的就有自…...

Apache AGE 安装部署
AGE概述 概述 我们可以通过源码安装、拉取docker镜像运行、直接使用公有云三种方式中的任意一种来使用Apache AGE 获取 AGE 发布版本 可以在 https://github.com/apache/age/releases 找到发布版本和发布说明。 源代码 源代码可以在 https://github.com/apache/age 找到…...
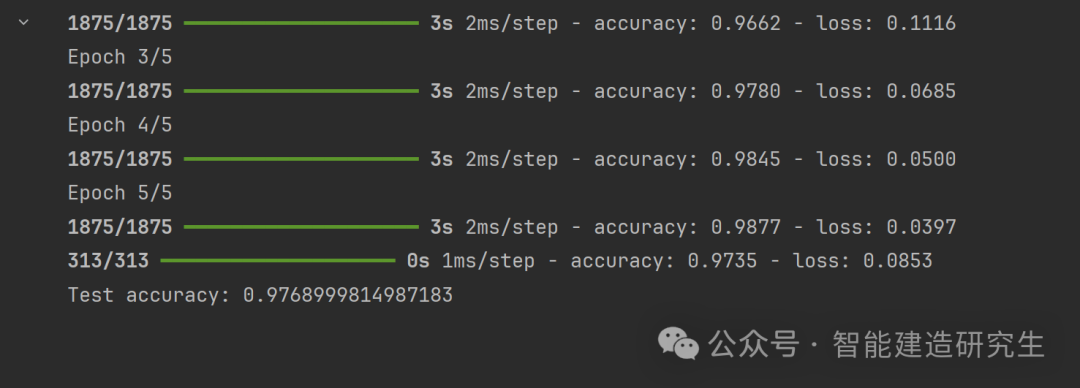
Python29 Tensorflow的基本知识和使用
1. TensorFlow TensorFlow 是一个开源的机器学习框架,由 Google Brain 团队开发。它用于数据流图的计算,尤其擅长深度学习任务。在 TensorFlow 中,数据流图(Data Flow Graph)是其核心概念之一,它定义了计算…...

Linux操作系统上用到的磁盘分区管理工具
parted磁盘分区工具 磁盘格式:MBR, GPT, 这两种名称分别是硬盘里面分区表两种格式的称呼, 第一种MBR格式的分区表最大支持2TB的容量, 磁盘的三种分区主分区,扩展分区,逻辑分区,主分区扩展分区<4 第…...

Python数据结构的库之Fuk使用详解
概要 fuk 是一个用于处理 Python 数据结构的库,全称为 "Fast and Uncomplicated Kit"。它提供了一系列高效、简洁的数据结构实现,以及对 Python 内置数据结构的扩展。通过使用 fuk,开发者可以更加方便地处理列表、集合、字典等数据类型,提高代码的执行效率和可读…...

【STM32学习】cubemx配置,串口的使用,串口发送接收函数使用,以及串口重定义、使用printf发送
1、串口的基本配置 选择USART1,选择异步通信,设置波特率 选择后,会在右边点亮串口 串口引脚是用来与其他设备通信的,如在程序中打印发送信息,电脑上打开串口助手,就会收到信息。 串口的发送接收࿰…...

复现MiDAS文章:文章数据和代码
介绍 MiDAS 4: A global catalogue of full-length 16S rRNA gene sequences and taxonomy for studies of bacterial communities in wastewater treatment plants 提供了全套的代码和数据,方便大家复现: github: https://github.com/ msdueholm/MiD…...

【Python专栏】Python的历史及背景介绍
博客主页:Duck Bro 博客主页系列专栏:Python专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Python的背景介绍 关键词:Python、优缺点、领域 目录 …...

web端已有项目集成含UI腾讯IM
通过 npm 方式下载 TUIKit 组件,将 TUIKit 组件复制到自己工程的 src 目录下: npm i tencentcloud/chat-uikit-vue mkdir -p ./src/TUIKit && rsync -av --exclude{node_modules,package.json,excluded-list.txt} ./node_modules/tencentcloud/…...
IF不降反增!审稿速度,比我家网速还快!3本接受率高的医学期刊,赶紧码住!
🔍 为什么选择这3本期刊? 今天老毕给大家分享3本医学 SCI,分别为Tumori Journal、Adipocyte以及Annals of Medicine。 这3本医学杂志,不仅审稿速度快,录用率还高,其中不乏接受率为48%的“毕业神刊”。2024年…...
怎样把视频字幕提取出来?分享4个零门槛的字幕提取工具
暑假正是弯道超车的好机会!相信不少朋友都会选择宅在家自学网课。 不可否认的是,海量学习资源的确可以让学习变得更加便捷与自由。然而,如何高效地吸收和理解在线课程也就成为了一个关键问题。不敢想倘若此时能够拥有一款高效又实用的视频提…...

PostgreSQL 里怎样解决多租户数据隔离的性能问题?
文章目录 一、多租户数据隔离的性能问题分析(一)大规模数据存储和查询(二)并发访问和锁争用(三)索引维护成本高(四)资源分配不均 二、解决方案(一)数据分区&a…...

Oracle执行一条SQL的内部过程
一、SQL语句根据其功能主要可以分为以下几大类: 1. 数据查询语言(DQL, Data Query Language) 功能:用于从数据库中检索数据,常用于查询表中的记录。基本结构:主要由SELECT子句、FROM子句、WHERE子句等组成…...

SpringMVC的架构有什么优势?——控制器(一)
#SpringMVC的架构有什么优势?——控制器(一) 前言 关键字: 机器学习 人工智能 AI chatGPT 学习 实现 使用 搭建 深度 python 事件 远程 docker mysql安全 技术 部署 技术 自动化 代码 文章目录 控制器(Controller) 控制器是S…...
LabVIEW干涉仪测向系统
开发了一套基于LabVIEW的软件系统,结合硬件设备,构建一个干涉仪测向实验教学平台。该平台应用于信号处理课程,帮助学生将理论知识与实际应用相结合,深化对信号处理核心概念的理解和应用。 项目背景: 当前信号处理教学…...
JavaScript 模拟光标全选选中一段文字
在JavaScript中,如果你想要通过编程方式选择一段文本,你可以使用window.getSelection()和Range对象。以下是一个简单的例子,展示了如何使用这些对象来选中页面上的特定文本节点: function selectText(node) {if (window.getSelect…...

【算法】代码随想录之数组(更新中)
文章目录 前言 一、二分查找法(LeetCode--704) 二、移除元素(LeetCode--27) 前言 跟随代码随想录,学习数组相关的算法题目,记录学习过程中的tips。 一、二分查找法(LeetCode--704࿰…...

Win-ARM联盟的端侧AI技术分析
Win-ARM联盟,端侧AI大幕将起 微软震撼发布全球首款AI定制Windows PC——Copilot PC,搭载全新NPU与重塑的Windows 11系统,纳德拉盛赞其为史上最快、最强、最智能的Windows PC。该设备算力需求高达40TOPS,支持语音翻译、实时绘画、文…...

MySQL常见的几种索引类型及对应的应用场景
MySQL 提供了多种索引类型,每种索引类型都有其特定的应用场景和优势。以下是 MySQL 中常见的几种索引类型及其具体应用场景: 1. B-Tree 索引 特点: B-Tree(Balanced Tree,平衡树)是 MySQL 的默认索引类型…...

如何利用java依赖jave-all-deps实现视频格式转换
视频格式转换是常见的需求,通过使用Java依赖库jave-all-deps可以实现视频格式的转换。本文将详细介绍在Java中如何利用jave-all-deps实现视频格式转换。 什么是jave-all-deps库? jave-all-deps是一款基于FFmpeg库的Java音视频编解码库。它提供了一系列AP…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
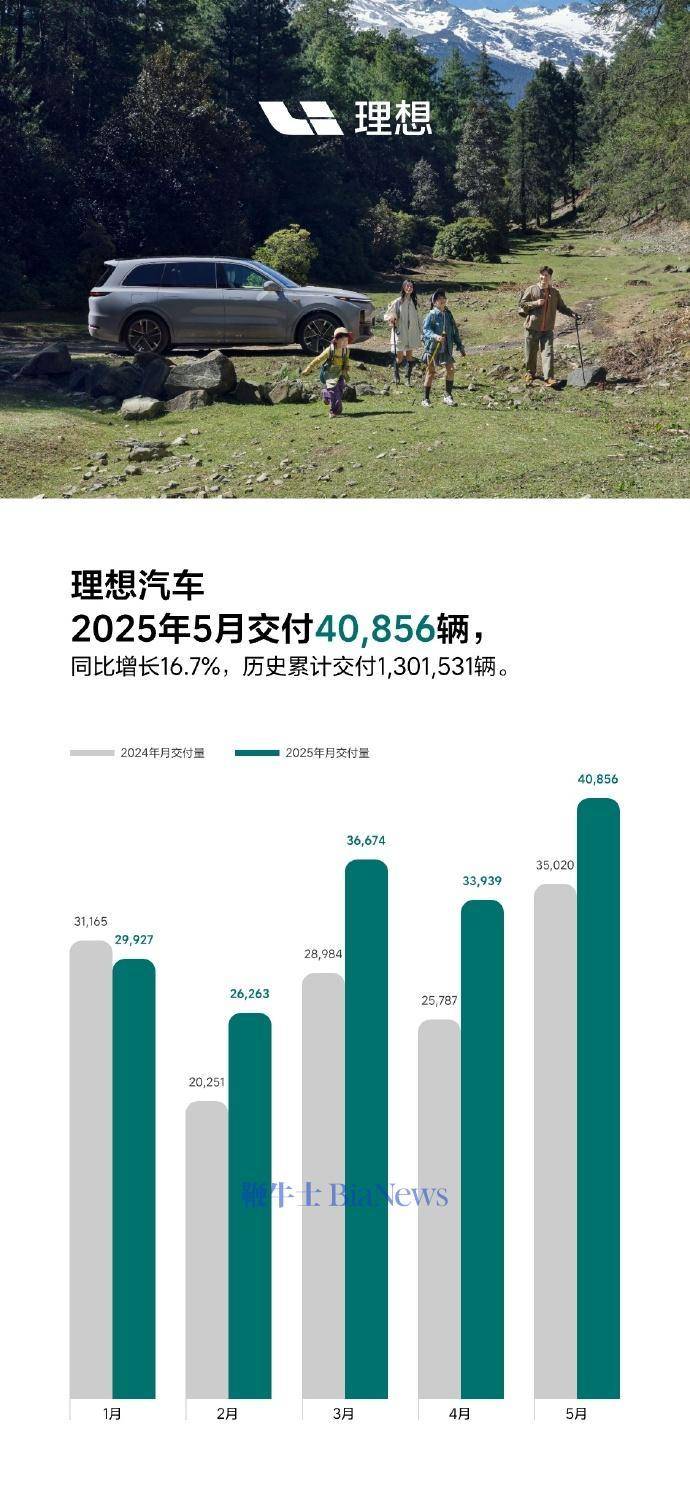
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
