根据H在有限域GF(2^m)上求解生成矩阵G
原理
有时间再补充。
注1:使用高斯消去法。如果Py不为单位阵,则说明进行了列置换,此时G不是系统形式。
注2:校验矩阵H必须是行满秩才存在对应的生成矩阵G,且生成矩阵G通常不唯一。
matlab实现:只做列置换,不做行置换
function [G, Px, Py] = Gaussian_Elimination_in_GFq(H, q)% initial[m, n] = size(H);H_stair = mod(H,q);Px = eye(m); Py = eye(n);for i=1:mfor j=i:nif gcd(H_stair(i,j), q) == 1break;elseif j==nerror('Gaussian_Elimination_in_GFq: The H is not full rank in GF(%d).',q);elsecontinue;endendendif j ~= iH_stair(:, [i, j]) = H_stair(:, [j, i]);Py(:, [i, j]) = Py(:, [j, i]);endendfor i=1:m[~, x, ~] = gcd(H_stair(i,i), q);inv_i = mod(x, q);H_stair(i, :) = mod(inv_i * H_stair(i, :), q);Px(i, :) = mod(inv_i * Px(i, :), q);for j=1:mif j~=i && H_stair(j,i)~=0factor=H_stair(j, i);H_stair(j, :) = mod(H_stair(j, :) - factor * H_stair(i, :), q);Px(j, :) = mod(Px(j, :) - factor * Px(i, :), q);endendendparity_matrix = mod((q-1).*H_stair(:,m+1:n),q);G_fixed=[parity_matrix',eye(n-m)];G=G_fixed*Py';
endmatlab实现:先做行置换,若无逆元,再做列置换
function [G, Px, Py] = Gaussian_Elimination_in_GFq(H, q)[m, n] = size(H);H_stair = mod(H,q);Px = eye(m); Py = eye(n);%% column findfor j=1:mfor i=j:mif gcd(H_stair(i,j), q) == 1break;elseif i==m%% row findfor k=j+1:nif gcd(H_stair(j,k), q) == 1break;elseif k==nerror('Gaussian_Elimination_in_GFq: The H is not full rank in GF(%d).',q);elsecontinue;endendend%% column exchangeH_stair(:,[j,k]) = H_stair(:,[k,j]);Py(:,[j,k]) = Py(:,[k,j]);i=j;break;elsecontinue;endendend%% row exchangeif i ~= jH_stair([j, i],:) = H_stair([i, j],:);Px([j, i],:) = Px([i, j],:);endendfor i=1:m[~, x, ~] = gcd(H_stair(i,i), q);inv_i = mod(x, q);H_stair(i, :) = mod(inv_i * H_stair(i, :), q);Px(i, :) = mod(inv_i * Px(i, :), q);for j=1:mif j~=i && H_stair(j,i)~=0factor=H_stair(j, i);H_stair(j, :) = mod(H_stair(j, :) - factor * H_stair(i, :), q);Px(j, :) = mod(Px(j, :) - factor * Px(i, :), q);endendendparity_matrix = mod((q-1).*H_stair(:,m+1:n),q);G_fixed=[parity_matrix',eye(n-m)];G=G_fixed*Py';end相关文章:
上求解生成矩阵G)
根据H在有限域GF(2^m)上求解生成矩阵G
原理 有时间再补充。 注1:使用高斯消去法。如果Py不为单位阵,则说明进行了列置换,此时G不是系统形式。 注2:校验矩阵H必须是行满秩才存在对应的生成矩阵G,且生成矩阵G通常不唯一。 matlab实现:只做列置…...

Django 实现子模版继承父模板
背景 Django的占位符,如果不继承父模板的内容,会被子模版所覆盖,有些业务场景子模版也需要使用到父模板中的内容 可以使用Django自带的标签{% block super %}来实现此效果 base.html 最基础html,相当于第一层html,bl…...

数据安全治理:从库级权限申请到表级权限申请
背景 随着数据安全意识的提高,企业越来越重视数据治理和权限管理。传统数仓大多对库级别进行读写授权,仅对人工标记的敏感库进行表级别授权,但由于敏感等级是由人为标记,错误率较高,故期望将权限申请流程细化到表级申…...

vue3源码(六)渲染原理-runtime-core
1.依赖关系 runtime-dom 依赖于runtime-core,runtime-core 依赖于reactivity和sharedruntime-core提供跨平台的渲染方法createRenderer,用户可以自己传递节点渲染的渲染方法renderOptions,本身不关心用户使用什么APIruntime-dom提供了为浏览器而生的渲染…...

python拆分Excel数据,自动发邮箱
import pandas as pd import poplib import email from email.header import decode_header from email.parser import Parser df = pd.read_excel("年假明细表.xlsx") depts = df["部门"].unique() for dept in depts: department_df = df[df[&q…...
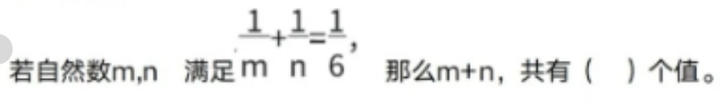
2024年福州延安中学夏季拿云杯拔尖创新人才素养测试(小高组)
1、选择题 那么,mn的值是( ) A、1243 B、1343 C、4029 D、4049 2、填空题 一副扑克牌共54张,其中1到13点各有 4张,每个数字黑色红色各两张,还有两张王牌,至少要取出( )…...
)
ES6 之 Promise 构造函数知识点总结 (四)
Promise 是异步编程的一种解决方案,比传统的解决方案——回调函数和事件——更合理和更强大。它由社区最早提出和实现,ES6 将其写进了语言标准,统一了用法,原生提供了 Promise 对象。 Promise 对象有以下两个特点。 对象的状态不受…...

KIVY 3D Rotating Monkey Head¶
7 Python Kivy Projects (With Full Tutorials) – Pythonista Planet KIVY 3D Rotating Monkey Head kivy 3D 旋转猴子头How to display rotating monkey example in a given layout. Issue #6688 kivy/kivy GitHub 3d 模型下载链接 P99 - Download Free 3D model by …...

测试几个 ocr 对日语的识别情况
测试几个 ocr 对日语的识别情况 1. EasyOCR2. PaddleOCR3. Deepdoc(识别pdf中图片)4. Deepdoc(识别pdf中文字)5. Nvidia neva-22b6. Claude 3.5 sonnet 识别图片中的文字7. Claude 3.5 sonnet 识别 pdf 中表格8. OpenAI gpt-4o 识…...

华为机考前准备工作
很多同学在刷完真题后,就直接去考试了,会发现不是卡在了题目的难度上,而是卡在了代码数据的如何输入上。为了避免各位有志之士忽略小细节而导致的前功尽弃,博主特意总结了华为机考试题数据输入的几种情况及其源代码,仅…...

偏差、方差(训练误差,验证误差)
目录 一、偏差、方差:二、正则化参数λ对偏差、方差的影响:三、训练集规模对偏差、方差的影响:四、模型复杂度对偏差、方差的影响:五、方差、偏差如何帮助训练:1.高偏差解决方法:2.高方差解决方法ÿ…...

Retrofit框架源码深度剖析【Android热门框架分析第二弹】
Android热门框架解析,你确定不来看看吗? OkHttp框架源码深度剖析【Android热门框架分析第一弹】 Retrofit框架源码深度剖析【Android热门框架分析第二弹】 什么是Retrofit? 准确来说,Retrofit 是一个 RESTful 的 HTTP 网络请求…...

C++Windows环境搭建(CLion)
文章目录 CLion下载安装CLion下载CLion安装新建项目新建一个文件基础设置字体设置clion中单工程多main函数设置 参考 CLion下载安装 CLion下载 打开网址:https://www.jetbrains.com/clion/download/ 点击Download进行下载。 CLion安装 双击下载好的安装包&…...

【区块链 + 智慧政务】省级一体化区块链平台 | FISCO BCOS应用案例
在加强数字政府建设的大背景下,科大讯飞广泛应用数字技术于政府管理服务,推动政府数字化、智能化运行。同时, 统筹推进业务、数据和技术的融合,提升跨地域、跨层级、跨部门和跨业务的协同管理和服务水平。 当前政务信息化建设中&…...

局域网远程共享桌面如何实现
在局域网内实现远程共享桌面,可以通过以下几种方法: 一、使用Windows自带的远程桌面功能: 首先,在需要被控制的电脑上右键点击“此电脑”,选择“属性”。 进入计算机属性界面后,点击“高级系统设置”&am…...

Ubuntu固定虚拟机的ip地址
1、由于虚拟机网络是桥接,所以ip地址会不停地变化,接下来我们就讲述ip如何固定 2、如果apt安装时报错W: Target CNF (multiverse/cnf/Commands-all) is configured multiple times in /etc/apt/sources.list:10, 检查 /etc/apt/sources.list…...

python破解密码·筛查和选择
破解密码时可能遇到的几种情况 ① 已知密码字符,破排序 ② 已知密码位数,破字符 ③ 已知密码类型,破字位 ④ 已知部分密码,破未知 ⑤ 啥都不知道,盲破,玩完 ⑥ 已知位数、字符、类型、部分密码中的几个&am…...

【将应用程序注册为系统服务】
在 Linux 系统中,将应用程序注册为系统服务可以使其在系统启动时自动运行,并且可以通过 systemctl 命令进行管理。/etc/systemd/system 目录是用于存放用户定义的 systemd 服务单元文件的目录。 将 Logstash 注册为系统服务 假设你已经安装了 Logstash…...

从0-1搭建一个web项目(路由目录分析)详解
本章分析vue路由目录文件详解 ObJack-Admin一款基于 Vue3.3、TypeScript、Vite3、Pinia、Element-Plus 开源的后台管理框架。在一定程度上节省您的开发效率。另外本项目还封装了一些常用组件、hooks、指令、动态路由、按钮级别权限控制等功能。感兴趣的小伙伴可以访问源码点个赞…...

Zabbix分布式监控
目录 分布式监控架构 实现分布式监控的步骤 优点和应用场景 安装Zabbix_Proxy Server端Web页面配置 测试 Zabbix 的分布式监控架构允许在大规模和地理上分散的环境中进行高效的监控。通过分布式监控,Zabbix 可以扩展其监控能力,支持大量主机和设备…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
