王道计算机数据结构+插入排序、冒泡排序、希尔排序、快速排序、简单选择排序
本内容是基于王道计算机数据结构的插入排序、冒泡排序、希尔排序、快速排序、简单选择排序整理。
文章目录
- 插入排序
- 算法
- 性能
- 代码
- 冒泡排序
- 算法
- 性能
- 代码
- 希尔排序
- 算法
- 性能
- 代码
- 快速排序
- 算法
- 性能
- 代码
- 简单选择排序
- 算法
- 性能
- 代码
插入排序
算法
算法思想:每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中,直到全部记录插入完成。
性能
- 空间复杂度:O(1)
- 时间复杂度:
- 最好:原本就有序;O(n)
- 最坏:原本为逆序;O(n2);
- 平均:O(n2);
- 稳定性:稳定;
代码
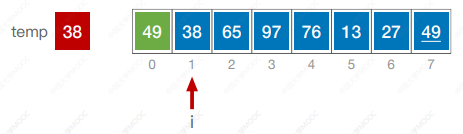
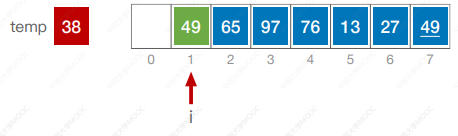
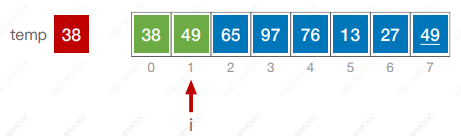
#include <iostream>
using namespace std;void InsertSort(int a[],int n) {int i, j, temp;for(i = 1; i < n; i++) {if (a[i] < a[i - 1]) {temp = a[i];for (j = i - 1; j >= 0 && a[j] > temp; j--) {a[j + 1] = a[j];}a[j + 1] = temp;}}
}void printfarray(int a[], int n) {for (int i = 0; i < n; i++) {cout << a[i] << " ";}cout << endl;
}int main() {int a[8] = {38, 49, 65, 97, 76, 13, 27, 49};int n = 8;cout << "插入排序前的数组为: ";printfarray(a, n);cout << endl;InsertSort(a,n);cout << "插入排序后的数组为: ";printfarray(a, n);cout << endl;
}

冒泡排序
算法
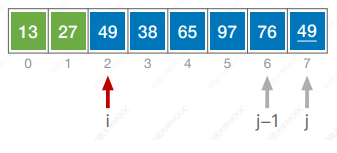
- 从后往前(或从前往后)两两比较相邻元素的值,若为逆序(即A[i-1]>A[i]),则交换它们,直到序列比较完。称这样过程为“一趟”冒泡排序。
- 第一趟排序使关键字值最小的一个元素“冒”到最前面;
- 每一趟排序都可以使一个元素移动到最终位置,已经确定最终位置的元素在之后的处理中无需再对比;
- 若某一趟排序没有发生“交换”,说明此时已经整体有序。
性能
- 空间复杂度:O(1)
- 时间复杂度:
- 最好:原本就有序;O(n)
- 最坏:原本为逆序;O(n2);
- 平均:O(n2);
- 稳定性:稳定;
代码
#include <iostream>
using namespace std;void swap(int &a, int &b){int temp = a;a = b;b = temp;
}void BubbleSort(int a[],int n) {for(int i = 0; i < n-1; i++) {bool flag = false; // 表示本趟冒泡是否发生交换的标志for (int j = n - 1; j > i; j--) {if (a[j-1] > a[j]) {swap(a[j-1],a[j]);flag = true;}}if (flag == false) {return;}}
}void printfarray(int a[], int n) {for (int i = 0; i < n; i++) {cout << a[i] << " ";}cout << endl;
}int main() {int a[8] = {38, 49, 65, 97, 76, 13, 27, 49};int n = 8;cout << "冒泡排序前的数组为: ";printfarray(a, n);cout << endl;BubbleSort(a,n);cout << "冒泡排序后的数组为: ";printfarray(a, n);cout << endl;
}

希尔排序
算法
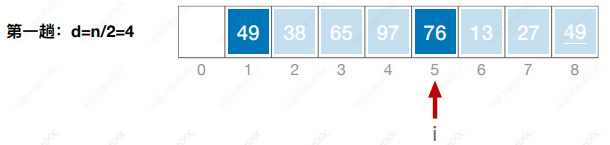
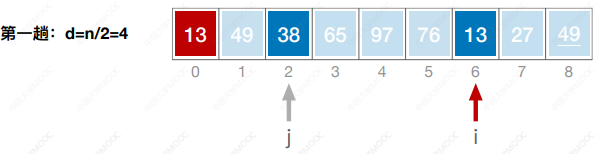
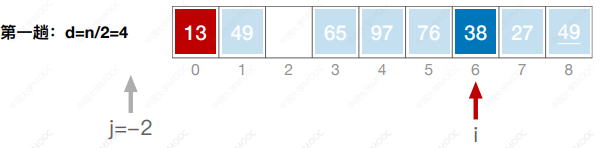
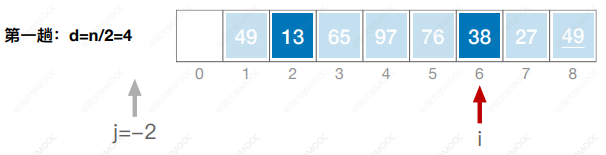
- 先将待排序表分割成若干形如L[i, i+d, i+2d, … ,i + kd]的“特殊”子表,对各个子表分别进行直接插入排序。缩小增量d,重复上述过程,直到d=1为止。
- 先追求表中元素部分有序,再逐渐逼近全局有序。
性能
- 空间复杂度:O(1)
- 时间复杂度:未知,但优于直接插入排序
- 稳定性:不稳定;
代码
#include <iostream>
using namespace std;void ShellSort(int a[],int n) {int i, j, d, temp;for (d = n / 2; d >= 1; d = d / 2) {for(i = d; i < n; i++) {if(a[i] < a[i-d]) {temp = a[i];for(j = i - d; j >= 0 && a[j] > temp; j-=d) {a[j + d] = a[j];}a[j + d] = temp;}}}
}void printfarray(int a[], int n) {for (int i = 0; i < n; i++) {cout << a[i] << " ";}cout << endl;
}int main() {int a[11] = {38, 6, 9, 3, 49, 65, 97, 76, 13, 27, 49};int n = 11;cout << "希尔排序前的数组为: ";printfarray(a, n);cout << endl;ShellSort(a,n);cout << "希尔排序后的数组为: ";printfarray(a, n);cout << endl;
}
快速排序
算法
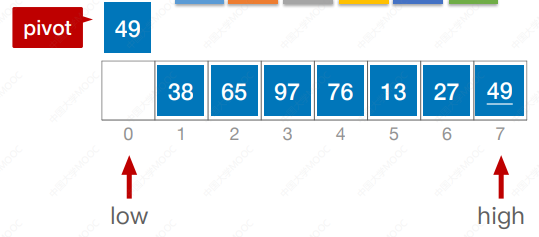
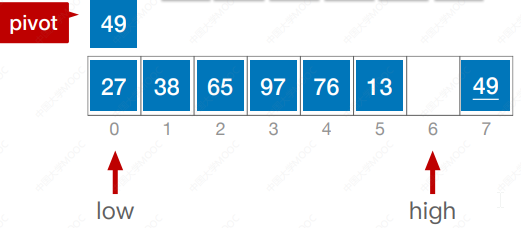
算法思想:在待排序表L[1 … n]中任取一个元素pivot作为枢轴(或基准,通常取首元素),通过一趟排序将待排序表划分为独立的两部分L[1 … k-1]和L[k+1 … n],使得L[1 … k-1]中的所有元素小于pivot,L[k+1 … n]中的所有元素大于等于pivot,则pivot放在了其最终位置L(k) 上,这个过程称为一次“划分”。然后分别递归地对两个子表重复上述过程,直至每部分内只有一个元素或空为止,即所有元素放在了其最终位置上。
算法表现主要取决于递归深度,若每次“划分”越均匀,则递归深度越低。“划分”越不均匀,递归深度越深。
性能
- 空间复杂度:
- 最好:O(n)
- 最坏:O(log(n))
- 时间复杂度:
- 最好:每次划分很均匀;O(n2)
- 最坏:原本为正序或逆序;O(n log(n));
- 平均:O(n log(n));
- 稳定性:不稳定;
代码
#include <iostream>
using namespace std;int Partition(int a[],int low, int high) {int pivot = a[low];while (low < high) {while(low < high && a[high] >= pivot) high--;a[low] = a[high];while(low < high && a[low] <= pivot) low++;a[high] = a[low];}a[low] = pivot;return low;
}void QuickSort(int a[],int low, int high) {if (low < high) {int pivotpos = Partition(a,low,high); // 划分QuickSort(a, low, pivotpos-1); // 划分左子表QuickSort(a, pivotpos + 1, high); // 划分右子表}
}void printfarray(int a[], int n) {for (int i = 0; i < n; i++) {cout << a[i] << " ";}cout << endl;
}int main() {int a[11] = {38, 6, 9, 3, 49, 65, 97, 76, 13, 27, 49};int n = 11;cout << "快速排序前的数组为: ";printfarray(a, n);cout << endl;QuickSort(a,0,n-1);cout << "快速排序后的数组为: ";printfarray(a, n);cout << endl;
}
简单选择排序
算法
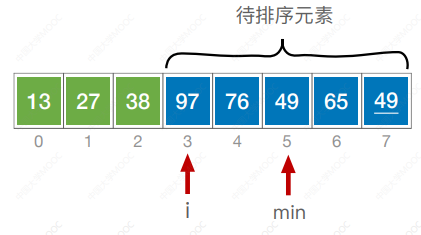
- 每一趟在待排序元素中选取关键字最小的元素加入有序子序列
- 必须进行总共 n - 1 趟处理;
性能
- 空间复杂度:O(1)
- 时间复杂度:O(n2)
- 稳定性:不稳定;
代码
#include <iostream>
using namespace std;void swap(int &a, int &b){int temp = a;a = b;b = temp;
}void SelectSort(int a[],int n) {for (int i = 0; i < n-1; i++) {int min = i;for(int j = i + 1; j < n; j++) {if (a[j] < a[min])min = j;}if (min != i) {swap(a[i],a[min]);}}
}void printfarray(int a[], int n) {for (int i = 0; i < n; i++) {cout << a[i] << " ";}cout << endl;
}int main() {int a[11] = {38, 6, 9, 3, 49, 65, 97, 76, 13, 27, 49};int n = 11;cout << "选择排序前的数组为: ";printfarray(a, n);cout << endl;SelectSort(a,n);cout << "选择排序后的数组为: ";printfarray(a, n);cout << endl;
}
相关文章:

王道计算机数据结构+插入排序、冒泡排序、希尔排序、快速排序、简单选择排序
本内容是基于王道计算机数据结构的插入排序、冒泡排序、希尔排序、快速排序、简单选择排序整理。 文章目录 插入排序算法性能代码 冒泡排序算法性能代码 希尔排序算法性能代码 快速排序算法性能代码 简单选择排序算法性能代码 插入排序 算法 算法思想:每次将一个…...
---多线程上篇)
python爬虫学习(三十三天)---多线程上篇
hello,小伙伴们!我是喔的嘛呀。今天我们来学习多线程方面的知识。 目录 一、了解多线程 (1)大概描述 (2)多线程爬虫的优势 (3)多线程爬虫的实现方式 (4)…...
JavaScript 原型链那些事
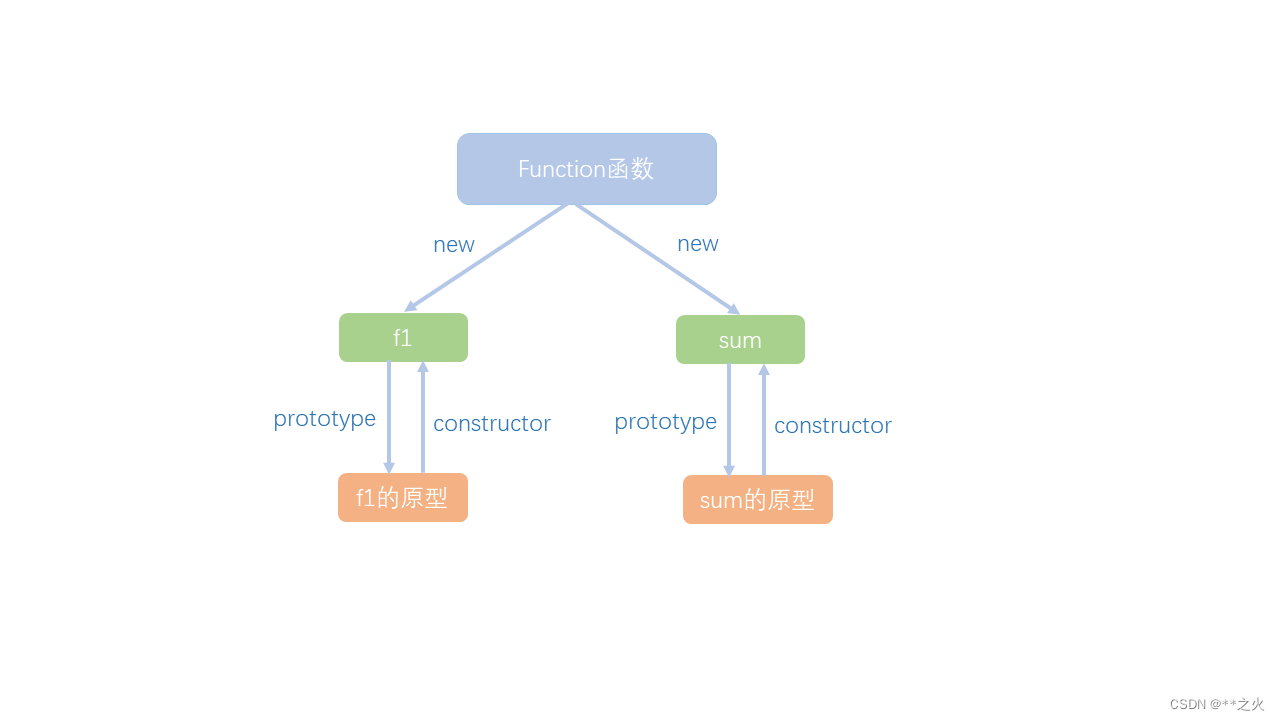
在讲原型之前我们先来了解一下函数。 在JS中,函数的本质就是对象,它与其他对象不同的是,创建它的构造函数与创建其他对象的构造函数不一样。那产生函数对象的构造函数是什么呢?是一个叫做Function的特殊函数,通过newFu…...

nginx的知识面试易考点
Nginx概念 Nginx 是一个高性能的 HTTP 和反向代理服务。其特点是占有内存少,并发能力强,事实上nginx的并发能力在同类型的网页服务器中表现较好。 Nginx 专为性能优化而开发,性能是其最重要的考量指标,实现上非常注重效率&#…...

每日Attention学习9——Efficient Channel Attention
模块出处 [CVPR 20] [link] [code] ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks 模块名称 Efficient Channel Attention (ECA) 模块作用 通道注意力 模块结构 模块代码 import torch import torch.nn as nn import torch.nn.functional …...

Java语言程序设计——篇三(1)
选择结构 概述选择单分支if语句例题讲解 双分支if-else语句例题讲解 条件运算符多分支的if-else语句例题讲解 嵌套的if语句例题讲解 switch语句结构例题讲解代码演示运行结果 概述 Java中的控制结构,包括: 1、选择结构( if、if-else、switch ) 2、循环结…...

基于SpringBoot实现轻量级的动态定时任务调度
在使用SpringBoot框架进行开发时,一般都是通过Scheduled注解进行定时任务的开发: Component public class TestTask {Scheduled(cron"0/5 * * * * ? ") //每5秒执行一次public void execute(){SimpleDateFormat df new SimpleDateFormat(…...

夸克升级“超级搜索框” 推出AI搜索为中心的一站式AI服务
大模型时代,生成式AI如何革新搜索产品?阿里智能信息事业群旗下夸克“举手答题”。7月10日,夸克升级“超级搜索框”,推出以AI搜索为中心的一站式AI服务,为用户提供从检索、创作、总结,到编辑、存储、分享的一…...
element-ui el-select选择器组件下拉框增加自定义按钮
element-ui el-select选择器组件下拉框增加自定义按钮 先看效果 原理:在el-select下添加禁用的el-option,将其value绑定为undefined,然后覆盖el-option禁用状态下的默认样式即可 示例代码如下: <template><div class…...

Python基于you-get下载网页上的视频
1.python 下载地址 下载 : https://www.python.org/downloads/ 2. 配置环境变量 配置 python_home 地址 配置 python_scripts 地址 在path 中加入对应配置 3. 验证 C:\Users>python --version Python 3.12.4C:\Users>wheel version wheel 0.43.04. 下载 c…...

大模型/NLP/算法面试题总结3——BERT和T5的区别?
1、BERT和T5的区别? BERT和T5是两种著名的自然语言处理(NLP)模型,它们在架构、训练方法和应用场景上有一些显著的区别。以下是对这两种模型的详细比较: 架构 BERT(Bidirectional Encoder Representation…...

vue3项目打包的时候,怎么区别测试环境,和本地环境
在Vue 3项目中区别测试环境和本地环境,并标记接口的方法可以通过环境变量来实现。 首先,你可以在你的项目根目录下创建一个.env文件,并定义你的环境变量。比如,你可以创建.env.local作为本地环境的配置文件,.env.test…...

小特性 大用途 —— YashanDB JDBC驱动的这些特性你都get了吗?
在现代数据库应用场景中,系统的高可用性和负载均衡是确保服务稳定性的基石。YashanDB JDBC驱动通过其创新的多IP配置特性,为用户带来了简洁而强大的解决方案,以实现数据库连接的高可用性和负载均衡,满足企业级应用的高要求。 01 …...

全网最全的软件测试面试八股文
前面看到了一些面试题,总感觉会用得到,但是看一遍又记不住,所以我把面试题都整合在一起,都是来自各路大佬的分享,为了方便以后自己需要的时候刷一刷,不用再到处找题,今天把自己整理的这些面试题…...

VMware虚拟机配置桥接网络
转载:虚拟机桥接网络配置 一、VMware三种网络连接方式 VMware提供了三种网络连接方式,VMnet0, VMnet1, Vmnet8,分别代表桥接,Host-only及NAT模式。在VMware的编辑-虚拟网络编辑器可看到对应三种连接方式的设置(如下图…...

华为机考真题 -- 攀登者1
题目描述: 攀登者喜欢寻找各种地图,并且尝试攀登到最高的山峰。地图表示为一维数组,数组的索引代表水平位置,数组的元素代表相对海拔高度。其中数组元素0代表地面。 一个山脉可能有多座山峰(山峰定义:高度大于相邻位置的高度,或在地图边界且高度大于相邻的高度)。登山者…...

深入理解Python密码学:使用PyCrypto库进行加密和解密
深入理解Python密码学:使用PyCrypto库进行加密和解密 引言 在现代计算领域,信息安全逐渐成为焦点话题。密码学,作为信息保护的关键技术之一,允许我们加密(保密)和解密(解密)数据。P…...

MMSegmentation笔记
如何训练自制数据集? 首先需要在 mmsegmentation/mmseg/datasets 目录下创建一个自制数据集的配置文件,以我的苹果叶片病害分割数据集为例,创建了mmsegmentation/mmseg/datasets/appleleafseg.py 可以看到,这个配置文件主要定义…...

Python基础语法:变量和数据类型详解(整数、浮点数、字符串、布尔值)①
文章目录 变量和数据类型详解(整数、浮点数、字符串、布尔值)一、变量二、数据类型1. 整数(int)2. 浮点数(float)3. 字符串(str)4. 布尔值(bool) 三、类型转换…...

【C++航海王:追寻罗杰的编程之路】关联式容器的底层结构——红黑树
目录 1 -> 红黑树 1.1 -> 红黑树的概念 1.2 -> 红黑树的性质 1.3 -> 红黑树节点的定义 1.4 -> 红黑树的结构 1.5 -> 红黑树的插入操作 1.6 -> 红黑树的验证 1.8 -> 红黑树与AVL树的比较 2 -> 红黑树模拟实现STL中的map与set 2.1 -> 红…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
