022-GeoGebra中级篇-几何对象之直线与坐标轴
本文主要介绍一下GeoGebra中直线的常见输入方式,比如工具栏输入、表达式输入、函数输入,最后再把坐标轴的调用简单介绍一下。内容比起传统的教学更偏向于实战一些,若感兴趣欢迎继续阅读。
目录
- 一、直线
- 1. 关于工具栏绘制
- (1)常用直线—lines集
- (2)常用直线—Contsruct集
- 2. 关于表达式的绘制
- (1)解析式方式
- (2)过两点建立
- 二、坐标轴
- 三、文章最后
一、直线
1. 关于工具栏绘制
有时候为了图快,我通常是采用工具栏输入与表达式输入相互结合的方式,比如过一点绘制一条垂线,我就直接用工具栏的垂线工具一拖就好了,当然,还需要返回到表达式栏看一下,比如修改下线的标签之类。
(1)常用直线—lines集
线段的创建非常简单,建议在表达式栏输入自己的两个点,然后在工具栏用线段工具一连就好了。


(2)常用直线—Contsruct集

这几种直线分别用来“过一点做直线的垂线”、“求线段的中垂线”、“过一点做线段的平行线”、“画角的角平分线”、“绘制圆的切线”,如果已经有点了,建议直接在这里用工具绘制就可以了,方便快捷。
2. 关于表达式的绘制
(1)解析式方式
g:3x+4y=2

解析式的方式记得前面写一个标签,然后跟上一个英文的冒号。
(2)过两点建立
“g:X=(-5,5)+t(4,-3)

这种属于解析式的变形,在数学中是不允许出现的,但是在GeoGebra中是可以出现的,输入后会根据这两个点直接计算出解析式。
二、坐标轴
坐标轴需注意的是被调用,两个坐标轴可以通过“xAxis”和“yAxis”指令被调用。
比如过(2,2)点做X轴的垂线,绘图后看一下表达式栏,可以发现是这样的:
f: PerpendicularLine(A,xAxis)
在这里xAxis就已经被调用了。

三、文章最后
若有任何问题都可以在这个铺子问客服,也会有资源相送,GeoGebra、PPT、平面动画、3D动画等各种技术都可以,祝好!

相关文章:

022-GeoGebra中级篇-几何对象之直线与坐标轴
本文主要介绍一下GeoGebra中直线的常见输入方式,比如工具栏输入、表达式输入、函数输入,最后再把坐标轴的调用简单介绍一下。内容比起传统的教学更偏向于实战一些,若感兴趣欢迎继续阅读。 目录 一、直线1. 关于工具栏绘制(1&#…...

node js安装、配置(Windows版)
目录 node js 安装 node js 全局配置 1、全局安装路径 2、全局缓存路径 3、修改环境变量 pnpm安装、卸载 全局安装pnpm 验证pnpm版本 卸载pnpm 1、移除全局安装的包 2、移除pnpm cli 脚本直接安装 npm安装的使用命令直接卸载 node js 安装 cmd 查看是否存在&…...
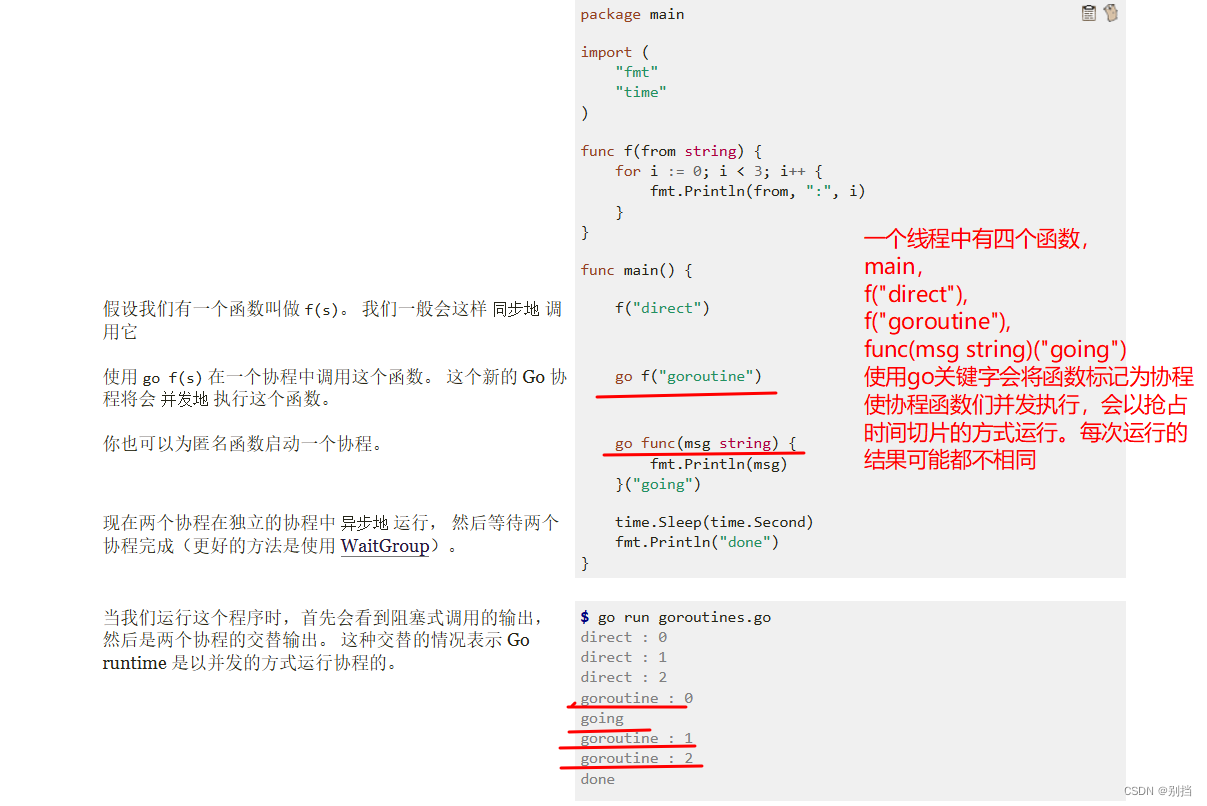
go语言day08 泛型 自定义错误处理 go关键字:协程
泛型: 抛错误异常 实现error接口类型 用java语言解释的话,实现类需要重写error类型的抽象方法Error().这样就可以自定义异常处理。 回到go语言,在Error()方法中用*argError 这样一个指针类来充当error接口的实现类。 在f2()方法中定义返回值…...

MySql性能调优01-[数据结构和索引]
数据结构和索引 什么是索引索引的种类常见索引数据结构和区别二叉树 红黑树 什么是索引 索引的种类 在Mysql中索引是在存储引擎层实现的,而不是在服务层实现的 按数据结构分:Btree索引、Hash索引、Full-text索引按存储结构分:聚簇索引、非聚…...

【算法入门-栈】逆波兰表达式求值
📖逆波兰表达式求值 ✅描述✅扩展:什么是逆波兰表达式✅题解方法一:栈✅题解方法二(数组模拟栈) 今天又刷了一道题,奥利给 刷题地址: 点击跳转 ✅描述 给定一个逆波兰表达式,求表达…...

【史上最全面ESP32教程】http通信
文章目录 前言HTTP协议是什么?HTTP协议的特点HTTP协议的常见应用 esp32 使用http通信通信流程基础使用HTTPClient 常用的函数函数介绍:void end(void);bool connected(void);void setReuse(bool reuse);void setUserAgent(const String& userAgent);…...
第二十七天 | 56. 合并区间、738. 单调递增的数字、968. 监控二叉树)
*算法训练(leetcode)第二十七天 | 56. 合并区间、738. 单调递增的数字、968. 监控二叉树
刷题记录 56. 合并区间*738. 单调递增的数字*968. 监控二叉树 56. 合并区间 leetcode题目地址 排序后遇到有重合的区间选择最大的区间保存即可,结果集中保存的是离当前区间最近的区间,因此使用当前区间与结果集中的最后一个集合比较查看是否有重合&…...

OpenJudge 奇数求和
目录 描述思路样例输入样例输出CodeCC 总时间限制: 1000ms 内存限制: 65536kB 描述 计算非负整数 m 到 n(包括m 和 n )之间的所有奇数的和,其中,m 不大于 n,且n 不大于300。例如 m3, n12, 其和则为:357911…...

【排序 - 快速排序】
快速排序(Quick Sort)是一种高效的排序算法,它基于分治(Divide and Conquer)的策略。这种排序算法的核心思想是选择一个基准元素,将数组分割成两部分,使得左边的元素都小于等于基准元素…...

pytest使用报错(以及解决pytest所谓的“抑制print输出”)
1. 测试类的类名问题 #codingutf-8import pytestclass TestClass1:def setup(self) -> None:print(setup)def test_01(self) -> None:print(test_01111111111111111111111)def test_02(self) -> None:print(test_02)以上述代码为例,如果类名是Test开头&am…...

开源项目编译harbor arm架构的包 —— 筑梦之路
GitHub - amy5200/harbor-arm64 先做个记录,空了再验证...

[笔记] SKF Enveloping FAQ 用户指南
文档编号:Application Note CM3013 1.名词解释: 1.1cavitationWhat Is Cavitation? | Pumps & Systems 叶片在液体中扰动形成的超声波 1.2 stiff machinehttps://suspensionlist.com/the-pros-and-cons-of-stiff-vs-soft-suspension-systems/ …...
 Part.3)
宪法学学习笔记(个人向) Part.3
宪法学学习笔记(个人向) Part 3 3. 国家基本制度 3.1 国家性质 3.1.1 国家性质概述 国家性质的概念 国家性质也称国体,或国家的阶级本质,是指各个阶级在国家中的地位(哪个阶层是统治阶层,哪个阶层是被统治阶层,哪个…...

联想拯救者Y7000 IRX9 笔记本接口功能介绍
适用机型:Legion Y7000 IRX9; 83JJ; USB(3.2 Gen 1)Type-接口摄像头开关组合音频插孔 多用于USB Type-C接口 以太网接口 多用途USB Type-C接口(支持USB Power Delivery)HDMI接口USB(3.2 Gen 1&…...

【ESP32】打造全网最强esp-idf基础教程——16.SmartConfig一键配网
SmartConfig一键配网 一、SmartConfig知识扫盲 在讲STA课程的时候,我们用的是代码里面固定的SSID和密码去连接热点,但实际应用中不可能这么弄,我们得有办法把家里的WiFi SSID和密码输入到设备里面去,对于带屏带输入设备还…...

MD5加密和注册页面的编写
MD5加密 1.导入包 npm install --save ts-md5 2.使用方式 import { Md5 } from ts-md5; //md5加密后的密码 const md5PwdMd5.hashStr("123456").toUpperCase(); 遇见的问题及用到的技术 注册页面 register.vue代码 <template><div class"wappe…...
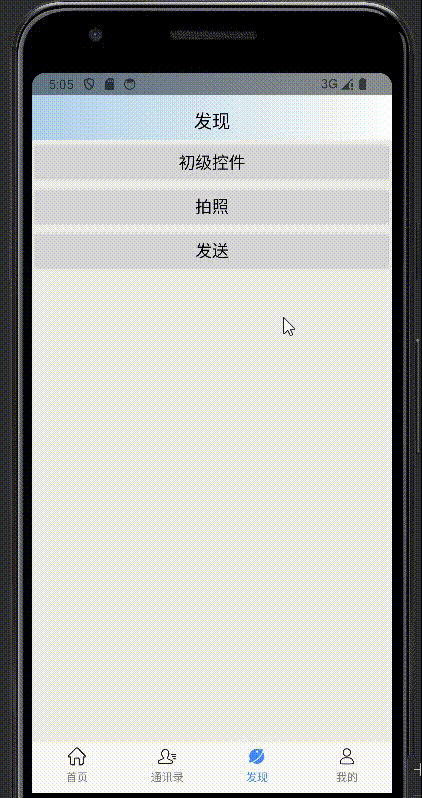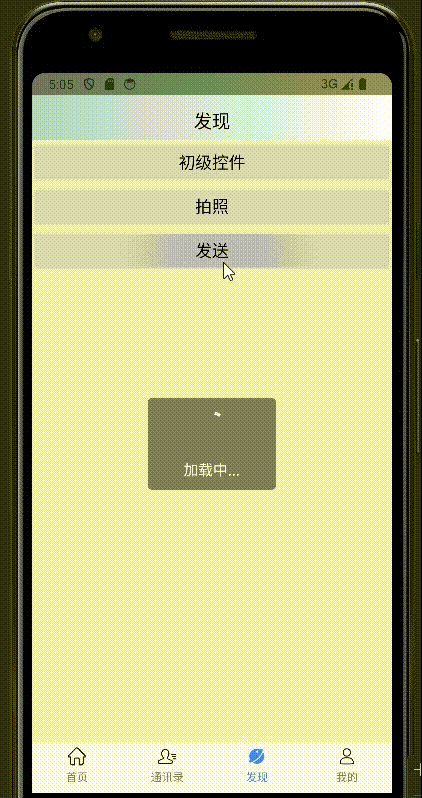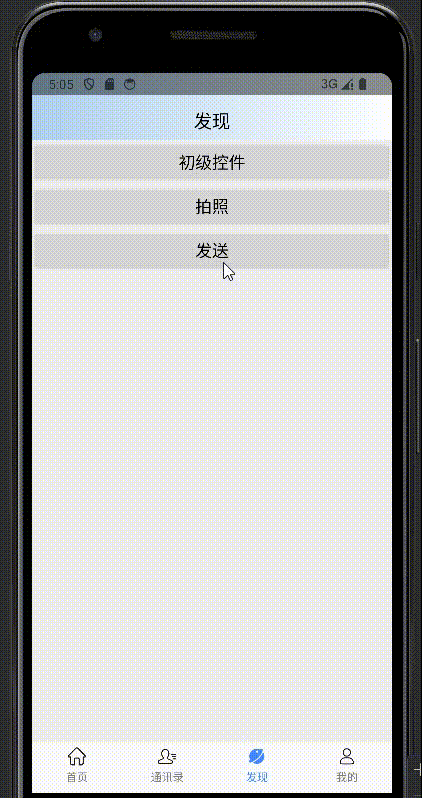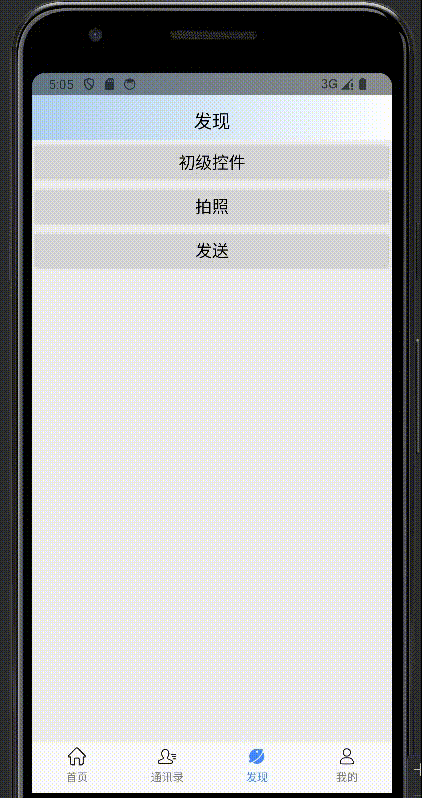
【Android组件】封装加载弹框
📖封装加载弹框 ✅1. 构造LoadingDialog✅2. 调用LoadingDialog 效果: ✅1. 构造LoadingDialog 构造LoadingDialog类涉及到设计模式中的建造者模式,进行链式调用,注重的是构建的过程,设置需要的属性。 步骤一&#x…...

Spring源码二十:Bean实例化流程三
上一篇Spring源码十九:Bean实例化流程二中,我们主要讨论了单例Bean创建对象的主要方法getSingleton了解到了他的核心流程无非是:通过一个简单工厂的getObject方法来实例化bean,当然spring在实例化前后提供了扩展如:bef…...

前端导出文件时,后端代码出错如何将错误信息返回给前端展示
功能说明:前端导出excel时,后端出现异常,比如sql异常,或者创建excel时出现的异常,希望将这些异常信息返回给前端查看。 框架:vue3 axios Springboot 实现难度分析:前端导出excel,…...

解决Spring Boot应用中的内存优化问题
解决Spring Boot应用中的内存优化问题 大家好,我是微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 1. Spring Boot应用的内存管理 在开发和部署Spring Boot应用时,有效地管理内存是确保应用性能和稳…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
