LeetCode 219. 存在重复元素 II
LeetCode 219. 存在重复元素 II
给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [1,2,3,1], k = 3
输出:true
示例 2:
输入:nums = [1,0,1,1], k = 1
输出:true
示例 3:
输入:nums = [1,2,3,1,2,3], k = 2
输出:false
提示:
1 <= nums.length <= 105
-109 <= nums[i] <= 109
0 <= k <= 105
哈希表
先构造哈希表,然后分析满足条件的值
class Solution:def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:d = defaultdict(list)for idx, num in enumerate(nums):d[num].append(idx)for num in d:if len(d[num]) < 2:continuefor i in range(len(d[num]) - 1):if (d[num][i + 1] - d[num][i]) <= k:return Truereturn False
借助哈希表渐进求值,666
class Solution:def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:pos = {}for i, num in enumerate(nums):if num in pos and i - pos[num] <= k:return Truepos[num] = ireturn False# 作者:力扣官方题解
# 链接:https://leetcode.cn/problems/contains-duplicate-ii/solutions/1218075/cun-zai-zhong-fu-yuan-su-ii-by-leetcode-kluvk/
# 来源:力扣(LeetCode)
# 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

LeetCode 219. 存在重复元素 II
LeetCode 219. 存在重复元素 II 给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] nums[j] 且 abs(i - j) < k 。如果存在,返回 true ;否则,返回 false 。 示例 1&am…...

【目标检测】使用自己的数据集训练并预测yolov8模型
1、下载yolov8的官方代码 地址: GitHub - ultralytics/ultralytics: NEW - YOLOv8 🚀 in PyTorch > ONNX > OpenVINO > CoreML > TFLite 2、下载目标检测的训练权重 yolov8n.pt 将 yolov8n.pt 放在ultralytics文件夹下 3、数据集分布 注…...
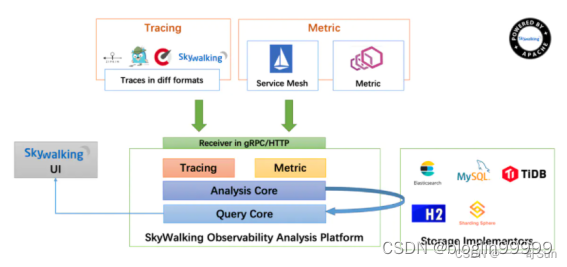
应用监控SkyWalking调研
参考: 链路追踪( Skyworking )_skywalking-CSDN博客 企业级监控项目Skywalking详细介绍,来看看呀-CSDN博客 SkyWalking 极简入门 | Apache SkyWalking 使用 SkyWalking 监控 ClickHouse Server | Apache SkyWalking https://zhuanlan.zhihu.com/p/3…...

Selenium使用注意事项:
find_element 和 find_elements 的区别 WebDriver和WebElement的区别 问题: 会遇到报错: selenium.common.exceptions.NoSuchElementException: Message: no such element: Unable to locate element: {"method":"css selector",&…...

小程序需要进行软件测试吗?小程序测试有哪些测试内容?
在如今移动互联网快速发展的时代,小程序已成为人们生活中不可或缺的一部分。然而,面对日益增长的小程序数量和用户需求,小程序的稳定性和质量问题日益突显。因此,对小程序进行软件测试显得尤为重要。 近期的一项调查显示…...

一文读懂企业租用GPU的注意事项!
在人工智能、大数据处理及高性能计算领域,GPU算力已成为推动技术创新与业务增长的核心动力。尚云Sunclouds作为GPU算力租赁服务提供商,为用户提供了灵活、高效且成本可控的解决方案。对于初次接触GPU算力租赁的用户而言,了解并掌握租用过程中…...

Linux运维:mysql主从复制原理及实验
当一台数据库服务器出现负载的情况下,需要扩展服务器服务器性能扩展方式有向上扩展,垂直扩展。向外扩展,横向扩展。通俗的讲垂直扩展是将一台服务器扩展为性能更强的服务器。横向扩展是增加几台服务器。 主从复制好比存了1000块钱在主上&…...

022-GeoGebra中级篇-几何对象之直线与坐标轴
本文主要介绍一下GeoGebra中直线的常见输入方式,比如工具栏输入、表达式输入、函数输入,最后再把坐标轴的调用简单介绍一下。内容比起传统的教学更偏向于实战一些,若感兴趣欢迎继续阅读。 目录 一、直线1. 关于工具栏绘制(1&#…...

node js安装、配置(Windows版)
目录 node js 安装 node js 全局配置 1、全局安装路径 2、全局缓存路径 3、修改环境变量 pnpm安装、卸载 全局安装pnpm 验证pnpm版本 卸载pnpm 1、移除全局安装的包 2、移除pnpm cli 脚本直接安装 npm安装的使用命令直接卸载 node js 安装 cmd 查看是否存在&…...
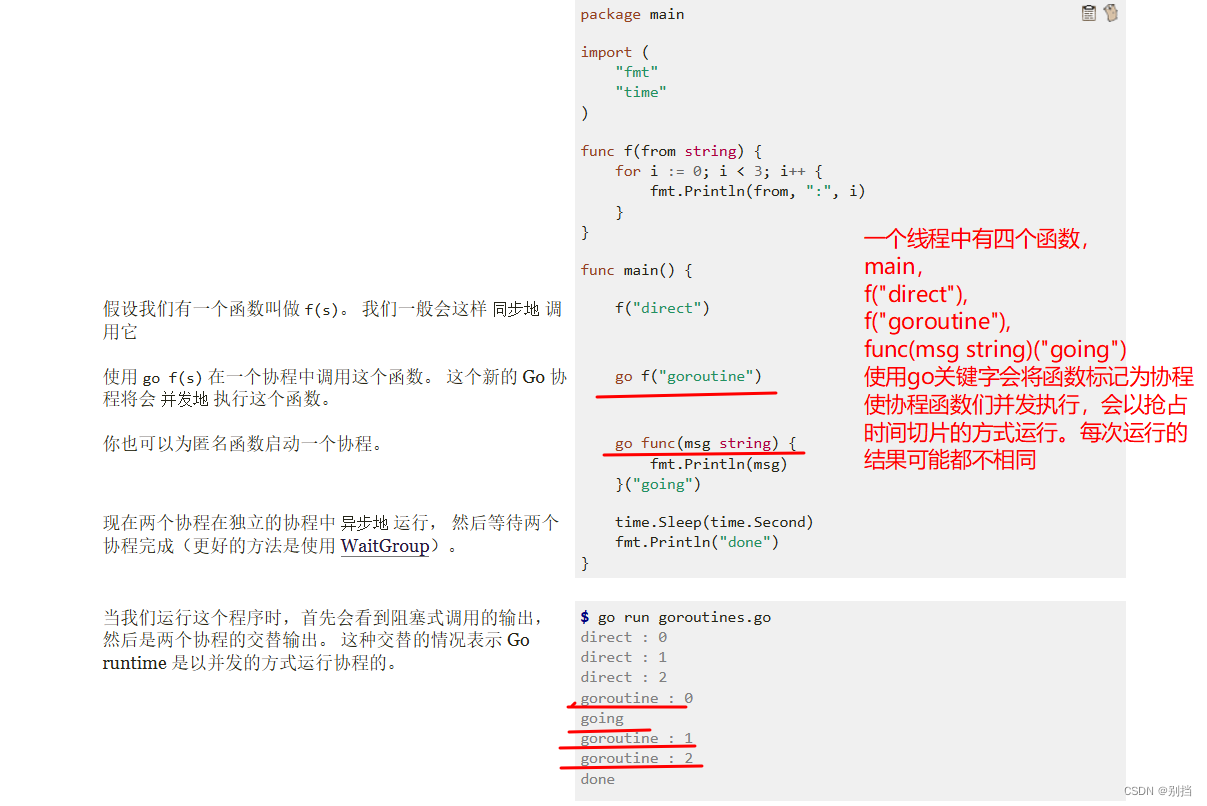
go语言day08 泛型 自定义错误处理 go关键字:协程
泛型: 抛错误异常 实现error接口类型 用java语言解释的话,实现类需要重写error类型的抽象方法Error().这样就可以自定义异常处理。 回到go语言,在Error()方法中用*argError 这样一个指针类来充当error接口的实现类。 在f2()方法中定义返回值…...

MySql性能调优01-[数据结构和索引]
数据结构和索引 什么是索引索引的种类常见索引数据结构和区别二叉树 红黑树 什么是索引 索引的种类 在Mysql中索引是在存储引擎层实现的,而不是在服务层实现的 按数据结构分:Btree索引、Hash索引、Full-text索引按存储结构分:聚簇索引、非聚…...

【算法入门-栈】逆波兰表达式求值
📖逆波兰表达式求值 ✅描述✅扩展:什么是逆波兰表达式✅题解方法一:栈✅题解方法二(数组模拟栈) 今天又刷了一道题,奥利给 刷题地址: 点击跳转 ✅描述 给定一个逆波兰表达式,求表达…...

【史上最全面ESP32教程】http通信
文章目录 前言HTTP协议是什么?HTTP协议的特点HTTP协议的常见应用 esp32 使用http通信通信流程基础使用HTTPClient 常用的函数函数介绍:void end(void);bool connected(void);void setReuse(bool reuse);void setUserAgent(const String& userAgent);…...
第二十七天 | 56. 合并区间、738. 单调递增的数字、968. 监控二叉树)
*算法训练(leetcode)第二十七天 | 56. 合并区间、738. 单调递增的数字、968. 监控二叉树
刷题记录 56. 合并区间*738. 单调递增的数字*968. 监控二叉树 56. 合并区间 leetcode题目地址 排序后遇到有重合的区间选择最大的区间保存即可,结果集中保存的是离当前区间最近的区间,因此使用当前区间与结果集中的最后一个集合比较查看是否有重合&…...

OpenJudge 奇数求和
目录 描述思路样例输入样例输出CodeCC 总时间限制: 1000ms 内存限制: 65536kB 描述 计算非负整数 m 到 n(包括m 和 n )之间的所有奇数的和,其中,m 不大于 n,且n 不大于300。例如 m3, n12, 其和则为:357911…...

【排序 - 快速排序】
快速排序(Quick Sort)是一种高效的排序算法,它基于分治(Divide and Conquer)的策略。这种排序算法的核心思想是选择一个基准元素,将数组分割成两部分,使得左边的元素都小于等于基准元素…...

pytest使用报错(以及解决pytest所谓的“抑制print输出”)
1. 测试类的类名问题 #codingutf-8import pytestclass TestClass1:def setup(self) -> None:print(setup)def test_01(self) -> None:print(test_01111111111111111111111)def test_02(self) -> None:print(test_02)以上述代码为例,如果类名是Test开头&am…...

开源项目编译harbor arm架构的包 —— 筑梦之路
GitHub - amy5200/harbor-arm64 先做个记录,空了再验证...

[笔记] SKF Enveloping FAQ 用户指南
文档编号:Application Note CM3013 1.名词解释: 1.1cavitationWhat Is Cavitation? | Pumps & Systems 叶片在液体中扰动形成的超声波 1.2 stiff machinehttps://suspensionlist.com/the-pros-and-cons-of-stiff-vs-soft-suspension-systems/ …...
 Part.3)
宪法学学习笔记(个人向) Part.3
宪法学学习笔记(个人向) Part 3 3. 国家基本制度 3.1 国家性质 3.1.1 国家性质概述 国家性质的概念 国家性质也称国体,或国家的阶级本质,是指各个阶级在国家中的地位(哪个阶层是统治阶层,哪个阶层是被统治阶层,哪个…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
